Extraction of Mechanical Properties with Second Harmonic Detection for Dynamic Nanoindentation Testing

Abstract

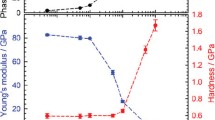
In this article, a new method based on the detection of the second harmonic of the displacement signal to determine mechanical properties of materials from dynamic nanoindentation testing, is presented. With this technique, the Young’s modulus and hardness of homogeneous materials can be obtained at small penetration depths from the measurement of the second harmonic amplitude. With this innovative method, the measurement of the normal displacement is indirectly used, avoiding the need for very precise contact detection. Moreover, the influence of the tip defect and thermal drift on the measurements are reduced. This method was used for dynamic nanoindentation tests performed on fused silica and on an amorphous polymer (PMMA) because these materials are supposed not to exhibit an indentation size effect at small penetration depths. The amplitude of the second harmonic of the displacement signal was correctly measured at small depths, allowing to calculate the Young’s modulus and the hardness of the tested materials. The mechanical properties calculated with this method are in good agreement with values obtained from classical nanoindentation tests.

Appendix: Second Harmonic Detection with Displacement Controlled Systems

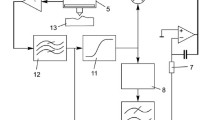
Continuous Stiffness Measurement Technique for Displacement Controlled Systems

The Continuous Stiffness Measurement method [8, 12, 13] consists in superimposing a harmonic displacement $\tilde{z}(t)$, at given frequency (from 30 to 100 Hz), to the displacement:

$$ \tilde{z}(t) = {z_1}{e^{{j\omega t}}} $$

(A1)

where z ₁ is the amplitude of the harmonic component and ω the circular frequency (rad/s). The load response is a series:

$$ \tilde{F}(t) = {F_1}{e^{{j(\omega t - {\phi_1})}}} + {F_2}{e^{{j(2\omega t - {\phi_2})}}} + ... + {F_n}{e^{{j(n\omega t - {\phi_n})}}} $$

(A2)

Where F _i , φ _i (i = 1…n) are respectively the amplitude and the phase of the harmonic components. The load response at the excitation frequency and the phase angle between load and displacement oscillation are measured continuously as a function of penetration depth. In order to determine the dynamic contact stiffness, the dynamic response of the system has to be determined. The frequency response function can be expressed by the following equation:

$$ \frac{{{F_1}}}{{{z_1}}}{e^{{ - j{\phi_1}}}} = K - {\omega^2}m + jD\omega $$

(A3)

where m is the column mass, D = D _i  + D _s is the global damping coefficient with D _i the damping due to the air in the gaps of the capacitor plates displacement sensing system, D _s the contact damping coefficient, $K = {\left( {\frac{1}{{{K_f}}} + \frac{1}{S}} \right)^{{ - 1}}} + {K_s}$ is the total dynamic stiffness with K _f the frame stiffness and K _s the support springs stiffness. In addition, the load signal is a function of the displacement signal modulated by an oscillation, so the load signal at the vicinity of z can be expanded as a Taylor development (at the second order here):

$$ F\left( {z + {z_1}{e^{{j\omega t}}}} \right) = F(z) + {z_1}{e^{{j\omega t}}}\frac{{dF(z)}}{{dz}} + \left( {\frac{{z_1^2{e^{{2j\omega t}}}}}{2}} \right)\frac{{{d^2}F(z)}}{{d{z^2}}} + ... $$

(A4)

Here, the Taylor development and the series (A2) are dependant of the harmonics terms of force and displacement. Considering equations (A2) and (A4), the harmonic terms of the series have to be equal term by term. For the first harmonic term, the following equality is obtained:

$$ {F_1}{e^{{ - j{\phi_1}}}} = {z_1}\frac{{dF(z)}}{{dz}} $$

(A5)

In this equation, the derivative of the force with respect to the displacement depends on the force and displacement amplitude, so according to equation (A3), the following equation is deduced:

$$ \frac{{dF(z)}}{{dz}} = \frac{{{F_1}}}{{{z_1}}}{e^{{ - j{\phi_1}}}} = K - {\omega^2}m + jD\omega $$

(A6)

So, the derivative of the load with respect to the displacement is equal to the frequency response function.

Second Harmonic Expression

Considering the second harmonic term, the following equation is obtained:

$$ {F_2}{e^{{ - j{\phi_2}}}} = \left( {\frac{{z_1^2}}{2}} \right)\frac{{{d^2}F(z)}}{{d{z^2}}} $$

(A7)

The above formula is interesting because the second harmonic of the load depends on the second derivative of the load with respect to the displacement. The second derivative can be computed by simply deriving equation (A6) with respect of z and by noticing that the only term which depends on the displacement variation is the dynamic contact stiffness.

Writing that: $\tan ({\varphi_1}) = \frac{{D\omega }}{{K - {\omega^2}m}}$, assuming that the support spring stiffness K _s is negligible compared to K , and using equations (A6) and (A7), the second derivative can be expressed by the following equation:

$$ \frac{{{d^2}F}}{{d{z^2}}} = \frac{{2\beta E_c^{*}\gamma {K^2}(1 + j\tan ({\phi_1}))}}{{{S^2}}} $$

(A8)

Equation (A7) can thus be rewritten in the following form:

$$ {F_2}{e^{{ - j{\phi_2}}}} = \frac{{z_1^22\beta E_c^{*}\gamma {K^2}(1 + j\tan ({\phi_1}))}}{{{S^2}}} $$

(A9)

By expressing the signal amplitude of load, the following equation is obtained:

$$ \left| {{F_2}} \right| = \frac{{{{\left| {{z_1}} \right|}^2}\left| \sqrt{1 + {{\tan }^2}({\phi_1})} \right|{K^2}\beta \gamma E_c^{*}}}{{{S^2}}} $$

(A10)

The dynamic stiffness K and the dynamic contact stiffness S are the most important parameters in the above equation, because all the other terms are constant. It was plotted theoretically by the ratio $\frac{{{K^2}}}{{{S^2}}}$ versus dynamic stiffness K (not shown). The dynamic contact stiffness S is calculated by the following equation:

$$ \frac{1}{S} = \frac{1}{K} - \frac{1}{{{K_f}}} $$

(A11)

with K _f being the frame stiffness. Let be K _f  = 500,000 N/m. This is the frame stiffness of the SA2®. The ratio $\frac{{{K^2}}}{{{S^2}}}$ decreases linearly when the harmonic stiffness increases. So, it is supposed that the load second harmonic amplitude decreases linearly during the indentation test. The expressions of the reduced contact modulus and the hardness can be obtained from equations (1) and (A11):

$$ E_c^{*} = \frac{{\left| {{F_2}} \right|{S^2}}}{{\beta \gamma {{\left| {{z_1}} \right|}^2}{K^2}\sqrt {{1 + {{\tan }^2}({\phi_1})}} }} $$

(A12)

$$ H = \frac{{4{S^2}{{\left| {{F_2}} \right|}^2}F}}{{{K^4}{{\left| {{z_1}} \right|}^4}\pi {\gamma^2}{{\left| {1 + {{\tan }^2}({\phi_1})} \right|}}}} $$

(A13)

In these equations, the dynamic stiffness K, the applied load F and the phase angle φ ₁ are measured by a classical nanoindentation technique using the CSM method, the circular frequency ω and the harmonic displacement amplitude z ₁. They are set before the test, the dynamic contact stiffness S and the derivative of the contact radius being set with respect to the tip displacement γ are then calculated, β being a constant given by literature. At last, the second harmonic amplitude of load F ₂ is measured with a lock-in amplifier. So, it is possible to determine the elastic modulus and the hardness of materials with second harmonic detection for displacement-controlled systems. Like load-controlled systems, as it can be observed in the above formulas, the displacement signal is not a parameter used in the equation. The displacement is only used to calculate γ, but this term, expressed in equation (20), is an easy-to-calculate constant (see paragraph V). Since it does not depend on displacement, but depends on displacement variation, it is thus not necessary to detect the contact very precisely. In addition, because the displacement measurement is not directly used, it is not needed to estimate the equivalent height of the tip defect.