A Novel Method for Strain Controlled Tests

Abstract

The present paper aims at providing a contribution to the testing strategies in the field of mechanics of materials, with particular reference to low cycle fatigue in the strain control mode. After a detailed analysis of the state of the art on possible techniques for strain controlling, the paper points out the difficulties that could be encountered when a conventional longitudinal contact extensometer cannot be used. This methodology, based on controlling the strain at a particular specimen location, by controlling the relative displacement between its ends, was developed to provide an alternative solution in such occurrences. The paper introduces its analytical fundamentals for its most general application in the execution of fatigue or even static tests. Particular attention was devoted to the validation of the proposed methodology: this task was conducted by applying the suggested technique to both static and fatigue testing of hourglass specimens, by analyzing results also in comparison to other experimentations or numerical simulations, always observing a good agreement. The methodology proved to be efficient and reliable on a wide range of strain amplitudes.

Appendices

Appendix 1: Computation of Integrals V and Z for a Specimen Having an Hourglass Shape

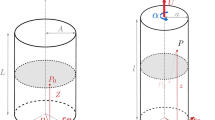
For an hourglass specimen, like that in Fig. 1, with a circular section in the central part with radius r₀ and a curvature radius R, the integrals V and Z can be computed as follows. The term l indicates the longitudinal length of the hourglass shape.

$$ V = \int\limits_0^{{{{l} \left/ {2} \right.}}} {\frac{{dx}}{{A(x)}}} = \int\limits_0^{{{{l} \left/ {2} \right.}}} {\frac{{dx}}{{\pi {{\left( {{r_0} + R - \sqrt {{{R^2} - {x^2}}} } \right)}^2}}}} $$

(A1)

$$ Z = \int\limits_0^{{{{l} \left/ {2} \right.}}} {\frac{1}{{{A^{{\frac{1}{n}}}}}}dx} = \int\limits_0^{{{{l} \left/ {2} \right.}}} {\frac{{dx}}{{\pi {{\left( {{r_0} + R - \sqrt {{{R^2} - {x^2}}} } \right)}^{{\frac{2}{n}}}}}}} $$

(A2)

Both integrals can be easily solved by numerical integration.

Appendix 2: Models by Hollomon [34], Swift [35] and Voce [36] and Applicability of the Proposed Method

The original model by Hollomon proposes a simple power law, to relate strain to stress.

$$ \sigma = {K_H}{\varepsilon^{{{n_H}}}} $$

(A3)

The equation (A3) can be inverted as follows, in order to determine strain as a function of stress.

$$ \varepsilon = {\left( {\frac{\sigma }{{{K_H}}}} \right)^{{\frac{1}{{{n_H}}}}}} $$

(A4)

This equation (equation (A4)) is very similar to the relationship proposed by Ramberg and Osgood [31], the only difference being the absence of the linear term. For this reason, it can be easily shown that displacement u can be related to force F, as in equation (A5).

$$ u = {\left( {\frac{{F{2^{{{n_H}}}}{Z_H}^{{{n_H}}}}}{{{K_H}}}} \right)^{{\frac{1}{{{n_H}}}}}} = {\left( {\frac{F}{{{K_{{Hu}}}}}} \right)^{{\frac{1}{{{n_H}}}}}} $$

(A5)

Where (equation (A6)),

$$ {K_{{Hu}}} = \frac{{{K_H}}}{{{{\left( {2{Z_H}} \right)}^{{{n_H}}}}}}; {Z_H} = \int\limits_0^{{{{l} \left/ {2} \right.}}} {{{\left( {\frac{1}{{A(x)}}} \right)}^{{\frac{1}{{{n_H}}}}}}dx} $$

(A5’)

The original model by Swift proposes equation (A6), to relate strain to stress.

$$ \sigma = {K_S}{\left( {\varepsilon + {\varepsilon_0}} \right)^{{{n_S}}}} $$

(A6)

The equation (A6) can be inverted as follows (equation (A7)), in order to determine strain as a function of stress.

$$ \varepsilon = - {\varepsilon_0} + {\left( {\frac{\sigma }{{{K_S}}}} \right)^{{\frac{1}{{{n_S}}}}}} $$

(A7)

The relative displacement between specimen blanks can be determined by integration, as shown in equation (A8).

$$ du = \varepsilon (x)dx \Leftrightarrow u = \int\limits_{{ - {{l} \left/ {2} \right.}}}^{{ + {{l} \left/ {2} \right.}}} {\varepsilon (x)dx} = 2\int\limits_0^{{ + {{l} \left/ {2} \right.}}} {\left[ { - {\varepsilon_0} + {{\left( {\frac{\sigma }{{{K_S}}}} \right)}^{{\frac{1}{{{n_S}}}}}}} \right]dx} $$

(A8)

By introducing equation (2), we obtain, equation (A9):

$$ u = 2\int\limits_0^{{ + {{l} \left/ {2} \right.}}} {\left[ { - {\varepsilon_0} + {{\left( {\frac{F}{{{K_S}A(x)}}} \right)}^{{\frac{1}{{{n_S}}}}}}} \right]dx} = - {\varepsilon_0}l + 2{\left( {\frac{F}{{{K_S}}}} \right)^{{\frac{1}{{{n_S}}}}}}\int\limits_0^{{{{l} \left/ {2} \right.}}} {{{\left( {\frac{1}{{A(x)}}} \right)}^{{\frac{1}{{{n_S}}}}}}dx} = - {\varepsilon_0}l + 2{\left( {\frac{F}{{{K_S}}}} \right)^{{\frac{1}{{{n_S}}}}}} \cdot {Z_S} $$

(A9)

Where, equation (A9’),

$$ {Z_S} = \int\limits_0^{{{{l} \left/ {2} \right.}}} {{{\left( {\frac{1}{{A(x)}}} \right)}^{{\frac{1}{{{n_S}}}}}}dx} $$

(A9’)

Finally, we obtain the equation (A10) in the F-u domain, which is formally equivalent to equation (A7) in the σ-ε domain.

$$ u = - {\varepsilon_0}l + {\left( {\frac{{F{2^{{{n_S}}}}{Z_S}^{{{n_S}}}}}{{{K_S}}}} \right)^{{\frac{1}{{{n_S}}}}}} = - {u_u} + {\left( {\frac{F}{{{K_{{Su}}}}}} \right)^{{\frac{1}{{{n_S}}}}}} $$

(A10)

Where,

$$ {u_u} = {\varepsilon_0}l; {K_{{Su}}} = \frac{{{K_S}}}{{{{\left( {2{Z_S}} \right)}^{{{n_S}}}}}} $$

(A10’)

Thus, after the experimental determination of the parameters K_Su and n_S in the F-u domain, it is possible to compute K_S, by applying equation (A10’), while the exponent n_S remains the same.

The original model by Voce proposes an exponential law, to relate strain to stress.

$$ \sigma = {\sigma_{\infty }} - {\sigma_{\infty }} \cdot \exp \left( { - {K_V}\varepsilon } \right) $$

(A11)

The equation (A11) can be inverted as follows, in order to determine strain as a function of stress.

$$ \varepsilon = - \frac{1}{{{K_V}}}\lg \left( {\frac{{{\sigma_{\infty }} - \sigma }}{{{\sigma_{\infty }}}}} \right) $$

(A12)

The relative displacement between specimen blanks can be determined by integration, as shown in equation (A13).

$$ du = \varepsilon (x)dx \Leftrightarrow u = \int\limits_{{ - {{l} \left/ {2} \right.}}}^{{ + {{l} \left/ {2} \right.}}} {\varepsilon (x)dx} = - 2\int\limits_0^{{ + {{l} \left/ {2} \right.}}} {\frac{1}{{{K_V}}}\lg \left( {\frac{{{\sigma_{\infty }} - \sigma }}{{{\sigma_{\infty }}}}} \right)dx} $$

(A13)

By introducing equation (2), we obtain, equation (A14):

$$ u = - \frac{2}{{{K_V}}}\int\limits_0^{{ + {{l} \left/ {2} \right.}}} {\lg \left( {\frac{{{\sigma_{\infty }} - \frac{F}{{A(x)}}}}{{{\sigma_{\infty }}}}} \right)dx} = - \frac{2}{{{K_V}}}\int\limits_0^{{{{l} \left/ {2} \right.}}} {\lg \left( {\frac{{{\sigma_{\infty }}A(x) - F}}{{{\sigma_{\infty }}A(x)}}} \right)dx} $$

(A14)

This integral cannot be analytically solved in a closed form. With a slight approximation, the function A(x) may be substituted by a “stairstep” function g(x), defined as follows.

Let {x₀, …, x_k, …, x_m} be a partition of the interval [0;l/2], with m having a sufficiently high value. Let x₀ = 0 and x_m = l/2, and let x_k be defined as follows (equation A15):

$$ {x_k} = \frac{l}{2}\frac{k}{m} $$

(A15)

Finally, let g: [0; l/2] → R be defined as follows. See also Fig. 10, where the functions A(x) and g(x) are plotted together, with reference to the hourglass geometry in Fig. 3(b):

$$ \begin{array}{*{20}{c}} {\forall x \in \left] {{x_k};{x_{{k + 1}}}} \right[,\left( {k = 0,...,m - 1} \right)} \hfill \\ {g(x) = {A_k} = A\left( {\frac{{{x_k} + {x_{{k + 1}}}}}{2}} \right)} \hfill \\ \end{array} $$

(A15’)

Fig. 10

Hourglass specimen cross section A vs. x and its approximation by the “stairstep” function g(x) (for sake of clarity, g(x) is sketched for a low value of m)

With reference to equation (A15’), it must be pointed out that the first value of the “stairstep” function, averaged between the coordinates x₀ and x₁, is A₀. This symbol has already been used in the paper text, to indicate the minimum area at the center of the hourglass shape. According to equation (A15’), the averaged value should be a bit higher, however the difference appears to be negligible, when considering a sufficiently high value of m. It can be clearly observed in Fig. 10, even for a not huge m value.

Consequently, with the aforementioned assumptions, the integral in equation (A14) can be written as follows (equation (A16)):

$$ u = - \frac{2}{{{K_V}}}\int\limits_0^{{{{l} \left/ {2} \right.}}} {\lg \left( {\frac{{{\sigma_{\infty }}A(x) - F}}{{{\sigma_{\infty }}A(x)}}} \right)dx} = - \frac{2}{{{K_V}}}\sum\limits_{{k = 0}}^{{m - 1}} {\left[ {\int\limits_{{{x_k}}}^{{{x_{{k + 1}}}}} {\lg \left( {\frac{{{\sigma_{\infty }}g(x) - F}}{{{\sigma_{\infty }}g(x)}}} \right)dx} } \right]} = - \frac{2}{{{K_V}}}\sum\limits_{{k = 0}}^{{m - 1}} {\left[ {\int\limits_{{{x_k}}}^{{{x_{{k + 1}}}}} {\lg \left( {\frac{{{\sigma_{\infty }}{A_k} - F}}{{{\sigma_{\infty }}{A_k}}}} \right)dx} } \right]} = - \frac{l}{{{K_V}}}\frac{1}{m}\sum\limits_{{k = 0}}^{{m - 1}} {\left[ {\lg \left( {\frac{{{\sigma_{\infty }}{A_k} - F}}{{{\sigma_{\infty }}{A_k}}}} \right)} \right]} = + \frac{l}{{{K_V}}}\frac{1}{m}\sum\limits_{{k = 0}}^{{m - 1}} {{u_k}} $$

(A16)

Where,

$$ {u_k} = - \lg \left( {\frac{{{\sigma_{\infty }}{A_k} - F}}{{{\sigma_{\infty }}{A_k}}}} \right) $$

(A16’)

The resulting displacement function, apart from the constant term l/K_V, can be regarded as an average of the m functions u_k. Some of them are plotted in Fig. 11 with reference to the A_k values of Fig. 10 and to σ_∞ = 1.000 MPa (typical value for the yield strength of a CRR steel). It can be observed that both u₀ and the resulting displacement function (defined for F < σ_∞A₀) tend to infinite as F → σ_∞A₀. By accepting an approximation in the transition between the elastic and the plastic behaviors, it is possible to write equation (A17). It expresses force asymptotic tendency to the value corresponding to yielding at the hourglass minimum section.

Fig. 11

Functions u_k(F), averaged displacement with asymptotic tendency (thick black line) and its estimate (thick grey line)

$$ \frac{1}{m}\sum\limits_{{k = 0}}^{{m - 1}} {{u_k}} \approx \beta {u_0} = - \beta \lg \left( {\frac{{{\sigma_{\infty }}{A_0} - F}}{{{\sigma_{\infty }}{A_0}}}} \right) = - \beta \lg \left( {\frac{{{F_{\infty }} - F}}{{{F_{\infty }}}}} \right) $$

(A17)

The term β is a suitably chosen constant, in order to have a good agreement between the averaged displacement and its estimate βu₀. With reference to the specimen geometry in Fig. 3(b), the value of β = 0.5 seems to be acceptable: both the averaged displacement and its estimate for the aforementioned value of β are plotted in Fig. 11: a good agreement can be remarked between the two curves. The parameter β may generally vary between 0 and 1, as a function of the specimen shape. A suggested procedure for its determination is presented below.

Thus, we have finally:

$$ u = - \frac{{l\beta }}{{{K_V}}}\lg \left( {\frac{{{F_{\infty }} - F}}{{{F_{\infty }}}}} \right) = - \frac{1}{{{K_{{Vu}}}}}\lg \left( {\frac{{{F_{\infty }} - F}}{{{F_{\infty }}}}} \right) $$

(A18)

The equation (A18) in the F-u domain is formally equivalent to equation (A12) in the σ-ε one, with the following relationship between model parameters:

$$ {F_{\infty }} = {\sigma_{\infty }}{A_0}; {K_{{Vu}}} = \frac{{{K_V}}}{{l\beta }} $$

(A18’)

Thus, after the experimental determination of the parameters F_∞ and K_Vu in the F-u domain, it is possible to compute σ_∞, and K_V by applying equation (A18’).

A suitable value of the term β for a generic specimen geometry can be determined, according to the following steps:

• Computation of the asymptotic value of stress σ_∞, by applying equation (A18’).

• Approximation of the function A(x) by a “stairstep” function, for a sufficiently high value of m, and consequent determination of A_k, for k = 0,…,(m-1)

• Computation of the functions u_k (equation (A16’)) for k = 0,…,(m-1) and determination of the averaged displacement.

• Determination of the optimal value for β, corresponding to the best agreement between the averaged displacement and its estimate βu₀.