Multiple-Camera Instrumentation of a Single Point Incremental Forming Process Pilot for Shape and 3D Displacement Measurements: Methodology and Results

Abstract

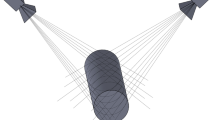
A multiple-camera system (more than two cameras) has been developed to measure the shape variations and the 3D displacement field of a sheet metal part during a Single Point Incremental Forming (SPIF) operation. The modeling of the multiple-camera system and the calibration procedure to determine its parameters are described. The sequence of images taken during the forming operation is processed using a multiple-view Digital Image Correlation (DIC) method and the 3D reconstruction of the part shape is obtained using a Sparse Bundle Adjustment (SBA) method. Two experiments that demonstrate the potentiality of the method are described.

Appendix: Modeling and Calibration of a Single Camera

In this Appendix, the modeling and the calibration of a single camera is presented in order to introduce the general methodology of our approach that has been extended to the modeling and calibration of a multiple-camera system (see Section “Modeling and Calibration of the Multiple-Camera System”).

A classical pinhole camera model (linear model) is used. A set of distortion parameters is added to this model to take into account the optical distortion of the lens (the model becomes non linear) [26].

As shown in Fig. 16, we denote $\mathcal{R}_\mathsf{w}$ the world coordinate system, $\mathcal{R}_\mathsf{c}$ the camera coordinate system (which has its origin at the lens center), $\mathcal{R}_\mathsf{r}$ the retinal coordinate system associated to the sensor plane and $\mathcal{R}_\mathsf{s}$ the image coordinate system (in pixel units).

Fig. 16

The three elementary transformations of the pinhole camera model, and the associated coordinate systems. The first transformation relates the coordinate of a scene point into the camera coordinate system. The second one is the projection transformation of this point onto the retinal plane. The third one transform the point into the sensor coordinate system (undistorted pixel)

The transformation that maps any 3D point M in $\mathcal{R}_\mathsf{w}$ into a 2D image-point m (in pixel units) consists of four consecutive transformations:

• 1. a transformation between $\mathcal{R}_\mathsf{w}$ and $\mathcal{R}_\mathsf{c}$. This is a rigid-body transformation (rotation R + translation t) L = (R, t), that transforms a 3D point M in $\mathcal{R}_\mathsf{w}$ into a 3D point M _c in $\mathcal{R}_\mathsf{c}$: M _c  = L(M)

• 2. a transformation between $\mathcal{R}_\mathsf{c}$ and $\mathcal{R}_\mathsf{r}$. This is a projective transformation P (imaging process) that transforms the 3D point M _c into a 2D point m _r in the retinal plane: m _r  = P(M _c )

• 3. a transformation between $\mathcal{R}_\mathsf{r}$ and $\mathcal{R}_\mathsf{s}$. This transformation describes the sampling of the intensity field incident on the sensor array. A 2D point m _r in the retinal plane (in metric units) is transformed into a 2D undistorted point m in the sensor image plane (in pixel units): $\tilde{m}=\mathbf{K}_\mathbf{k}(m_r)$.

  This transformation depends on the five camera intrinsic parameters k = (c _x , c _y , f _x , f _y , s), where c _x and c _y are the coordinates of the principal point (in pixel units), given by the intersection of the optical axis with the retinal plane, f _x and f _y are the focal length in pixels in the x and y direction, and s is the skew factor.

• 4. a transformation D _d that transforms an ideal undistorted pixel into a distorted pixel: $m=\mathrm{D_\mathbf{d}}(\tilde{m})$.

  This transformation depends on several distortions parameters.⁸ The number of distortion parameters (typically from 1 to 7) depends on the distortion model that is used [26]. In the sequel, we will suppose that a 3-parameter-distortion-model is used (3rd order radial distortion model).

The composition of these four transformations can be written:

$$ f{\kern-.7pt} :{\kern-.7pt}\begin{array}[t]{ccc} \mathbb{R}^{5}{\kern-.7pt} \times{\kern-.7pt} \mathbb{R}^{3}{\kern-.7pt} \times{\kern-.7pt} \mathbb{R}^{3}{\kern-.7pt} \times{\kern-.7pt} \mathbb{R}^{3}{\kern-.7pt} \times{\kern-.7pt} \mathbb{R}^{3} & \longmapsto & \mathbb{R}^{2}\\ \left(\mathbf{k},\mathbf{d},\mathbf{R},\mathbf{t},M\right) &\longmapsto & m = \mathrm{D_\mathbf{d}}(\mathbf{K}_\mathbf{k}(\mathbf{P}(\mathbf{L}(M)))) \end{array} $$

(4)

and leads to the following equation that relates a 3D point in space M and its 2D projection m onto the camera sensor array (pixel coordinates) :

$$ m=\mathrm{f}(\mathbf{k},\mathbf{d},\mathbf{R},\mathbf{t},M)=\mathrm{f}_{\mathbf{k},\mathbf{d},\mathbf{L}}(M) $$

(5)

Calibrating the camera consists in determining its parameters k, d, R and t. The experimental calibration procedure generally uses a calibration target that provides known 3D points. In our work, the calibration is performed by acquiring a series of n images of a planar calibration target made up of p circular points, observed at different positions and orientations (see Fig. 17). Thus, the calibration target provides a set of p known 3D points.

Fig. 17

Procedure for calibrating a single camera: a series of images of a planar calibration target observed at different positions and orientations is acquired by the camera

We call $m_i^j$ the 2D projection into the camera image plane of the jth 3D point M _j (j = 1...p) of the ith view (i = 1...n). We define a set of localization matrices L _i  = (R _i , t _i ) (i = 1...n) that represent the ith position of the calibration target with respect to camera reference frame (see Fig. 17).

The estimation of the parameters in the least-square sense leads to a non-linear optimization process, where the sum of the 2D Euclidean distance between the estimated projection of the j-th point of the i-th view onto the camera (using equation (5)) and the actual image-point $m_i^j$ extracted in the i-th image is minimized:

$$ \theta = \arg\min\limits_\theta\sum\limits_{i=1}^n\sum\limits_{j=1}^p \Vert m_i^j - \mathrm{f}\left(\mathbf{k}, \mathbf{d}, \mathbf{R}_i, \mathbf{t}_i, M_j\right) \Vert^2 $$

(6)

where θ = (k, d, R ₁...R _n , t ₁...t _n , M ₁...M _p ) is the vector of the 8 + 6 n + 3 p parameters that are estimated during the minimization process. It should be noted that there are 2 n p equations (each 3D point projection gives two relations). With a judicious choice of n and p, there are more equations than unknowns (over-determined system).

The estimation of the camera intrinsic parameters k and d, the extrinsic parameters R _i and t _i of each view, and the 3D points M _j of the calibration target is a well-known problem referred to as Bundle Adjustment [25, 29]. It is solved using the Levenberg-Marquardt algorithm. In order the algorithm to converge, an initial guess of the parameters is required. An initial guess of the 5 intrinsic parameters (vector k) and of the extrinsic parameters related to each view (R _i and t _i ) is computed using the closed-form solution described in [30] or [31]. The distortion parameters (vector d) are simply initialized to 0. An initial guess of the 3D points (M _j ) is given by the user supplied model of the target. As the points of the target will be re-estimated, the initial model need not be known accurately which is a great advantage of this calibration method.