A New Procedure for the Evaluation of Non-Uniform Residual Stresses by the Hole Drilling Method Based on the Newton-Raphson Technique

Abstract

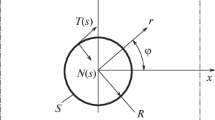
The hole drilling method is one of the most used semi-destructive techniques for the analysis of residual stresses in mechanical components. The non-uniform stresses are evaluated by solving an integral equation in which the strains relieved by drilling a hole are introduced. In this paper a new calculation procedure, based on the Newton-Raphson method for the determination of zeroes of functions, is presented. This technique allows the user to introduce complex and effective forms of stress functions for the solution of the problem. All the relationships needed for the evaluation of the stresses are obtained in explicit form, eliminating the need to use additional mathematical tools. The technique is based on a rather general theory that allows to obtain the formulations of various existing techniques as particular cases.

Appendix

In this appendix some details about the numerical implementation of the (A) e (B) applications of the GM are given. An example in MATLAB® programming language is also reported.

The most relevant steps of the implementation are the numerical evaluation of the integrals (25, 26) and (13′, 16′), Jacobian vector and Hessian matrix, and the integrals (24) and (29), I(z) functions. In the proposed applications they have been evaluated by applying the trapezoidal rule, a simple but effective method for the approximated evaluation of the integral of a function f(x) known in a discrete set of points x _k . In general, the solving relationship can be written as follows:

$$ \int\limits_{{x^{(i)}}}^{{x^{(i + 1)}}} {f(x)dx} \approx \frac{1}{2}\sum\limits_{k = i{k^{(i)}}}^{i{k^{(i + 1)}} - 1} {\left[ {f\left( {{x_{k + 1}}} \right) + f\left( {{x_k}} \right)} \right]\left( {{x_{k + 1}} - {x_k}} \right)} $$

(A1)

in which ik ⁽ⁱ⁾ is the index of the point x _k corresponding to the extreme x ⁽ⁱ⁾ of the interval of integration (i.e. for which it is x _ik ⁽ⁱ⁾ = x ⁽ⁱ⁾).

In the integrals (25, 26), the function $e(z,{\mathbf{\bar c}})$ (3) appears. It depends directly from the experimental strains p(ζ _k ) according to equation (5). The experimental strains can be introduced in the equations directly or using some fitting/smoothing function. In the first case the $e(z,{\mathbf{\bar c}})$ function is known only at the points where z = ζ _k , being

$$ e\left( {{\xi_k},{\mathbf{\bar c}}} \right) = p\prime \left( {{\xi_k},{\mathbf{\bar c}}} \right) - p\left( {{\xi_k}} \right) $$

(A2)

According to (A1) and (A2), the integral (25) can be numerically evaluated by means of the following expression:

$$ J_j^{(i)} = 2\int\limits_{{z^{(i)}}}^{{z^{(i + 1)}}} {e(z)I_j^{(i)}(z)dz \approx \sum\limits_{k = i{k^{(i)}}}^{i{k^{(i + 1)}} - 1} {\left[ {e\left( {{\xi_{k + 1}}} \right)I_j^{(i)}\left( {{\xi_{k + 1}}} \right) + e\left( {{\xi_k}} \right)I_j^{(i)}\left( {{\xi_k}} \right)} \right]\left( {{\xi_{k + 1}} - {\xi_k}} \right)} } $$

(A3)

The I _j ⁽ⁱ⁾(z) functions can be determined calculating the corresponding integrals (24) in each ζ _k point. The integration is carried out along the Z variable, in particular, calculating the F(Z,z) function at discrete quotes Z _iZ , equation (24) can be written as:

$$ I_j^{(i)}\left( {{\xi_k}} \right) = \int\limits_{{z^{(i)}}}^{{z^{(i + 1)}}} {{Z^j}F(Z,{\xi_k})dZ} \approx \frac{1}{2}\sum\limits_{iZ = i{z^{(i)}}}^{i{z^{(i + 1)}} - 1} {\left[ {Z_{iZ + 1}^j\;F({Z_{iZ + 1}},{\xi_k}) + Z_{iZ}^j{ }F({Z_{iZ}},{\xi_k})} \right]\left( {{Z_{iZ + 1}} - {Z_{iZ}}} \right)} $$

(A4)

The evaluation of the terms of the Hessian matrix (26) can be carried out in a way similar to that described for the terms of the Jacobian vector.

It has to be noted that better results are more often obtained if the extremes of the intervals are chosen from the hole depths ζ _k .

In the (B) case of the GM, the e(z,c) function is simplified to

$$ e\left( {{\xi_k},{\mathbf{c}}} \right) = - p\left( {{\xi_k}} \right) $$

(A5)

and the terms of the Jacobian vector (13′) can be calculated by the following relationship, according to (A1):

$$ {J_j} = - 2\int\limits_0^{{z_M}} {p\left( {{\xi_k}} \right)\frac{{p\prime \left( {{\xi_k},{\mathbf{c}}} \right)}}{{\partial {c_j}}}dz} \approx \frac{1}{2}\sum\limits_{k = 1}^{M - 1} {\left[ {p\left( {{\xi_{k + 1}}} \right)\frac{{p\prime \left( {{\xi_{k + 1}},{\mathbf{c}}} \right)}}{{\partial {c_j}}} + p\left( {{\xi_k}} \right)\frac{{p\prime \left( {{\xi_k},{\mathbf{c}}} \right)}}{{\partial {c_j}}}} \right]\left( {{Z_{k + 1}} - {Z_k}} \right)} $$

(A6)

The derivatives of the p function can be obtained by equations (34–36). Equation (34) can be written in discrete form as

$$ \frac{{\partial p\prime \left( {{\xi_k},{\mathbf{c}}} \right)}}{{\partial {c_j}}} = {I_{j,1}}\left( {{\xi_k}} \right) + \sum\limits_{l = 1}^2 {\left[ {{i_{j,l}}{ }{I_{j,l}}\left( {{\xi_k}} \right) - {i_{j - 1,l}}{ }{I_{j - 1,l}}\left( {{\xi_k}} \right)} \right]} \quad \quad j = {2} \ldots m $$

(A7)

The discrete form of equations (35–36) can be easily derived from equation (A7). The terms I _j,l(ζ _k ) in (A7) are expressed by equation (32), that can be written in discrete form as

$$ {I_{j,l}}\left( {{\xi_k}} \right) = \int\limits_{{z_j}}^{{z_{j + 1}}} {{Z^{l - 1}}{ }F(Z,{\xi_k})dZ \approx \frac{1}{2}\sum\limits_{iZ = i{z_j}}^{i{z_{j + 1}} - 1} {\left[ {Z_{iZ + 1}^{l - 1}{ }F({Z_{iZ + 1}},{\xi_k}) + Z_{iZ}^{l - 1}{ }F({Z_{iZ}},{\xi_k})} \right]\left( {{Z_{iZ + 1}} - {Z_{iZ}}} \right)} } $$

(A8)

In the following, the implementations of the GM (A) and (B) version in MATLAB® programming language are reported. In particular two functions called GM_A and GM_B are described. These return as output the constants c for the two cases, receiving as input the following data:

• two row vectors containing the measured strains p(ζ _k ) and the relative quotes ζ _k ,

• a matrix containing the values of the influence function F(Z,ζ _k ) calculated at the points Z and ζ _k and a row vector containing the coordinates Z,

• a row vector containing the quotes z ⁽ⁱ⁾ of the intervals of definition of the polynomials, for (A) case, or the extremes of the broken line z _j for (B) case,

• the degree of the polynomials j _M , only for (A) case.

In the two subroutines the following symbols are used:

• p = p(ζ _k ), relaxed strains;

• zk = ζ _k , depths of the hole;

• F = F(Z,ζ _k ), values of the influence function;

• Z = Z, Z values;

• M = M, number of steps.

In subroutine GM_A are also used

• ${\hbox{c}} = {\mathbf{\bar c}}$, matrix whose rows are the c⁽ⁱ⁾ vectors;

• zi = z ⁽ⁱ⁾, extremes of intervals of polynomials;

• n = n, number of polynomials, number of intervals z ⁽ⁱ⁾ ≤ Z ≤ z ⁽ⁱ⁺¹⁾, number of c ⁽ⁱ⁾ vectors (number of rows of c matrix);

• ${\hbox{n1}} = n + {1}$, number of the ordinates of the extremes of the intervals;

• jM = j _M , degree of polynomials;

• ${\hbox{jM1}} = {j_M} + {1}$, number of coefficients of the polynomials, number of elements of the c⁽ⁱ⁾ vectors (number of columns of c matrix);

• ${\hbox{pf}} = p\prime ({\zeta_k},{\mathbf{\bar c}})$, calculated strains.

In subroutine GM_B are also used

• c = c, vector of c costants;

• zj = z _j , extremes of the segments of the broken line;

• m = m, number of segments of the broken line;

• ${\hbox{m1}} = m + {1}$, number of the ordinates of the extremes of the segments, number of elements of c vector.

In MATLAB® programming language the calculation of the integrals by the trapezoidal rule of equation (A1), applied in equations (A3, A4, A6, A8), is carried out by the function called trapz, that uses as input the vectors containing the positions x _k and the corresponding values of the f(x) functions.

In the proposed subroutines, the determination of the indexes of the elements of the arrays corresponding to the extremes of integration, indicated as ik and iz in equations (A3, A4, A8), is carried out by the MATLAB® function called find.

The symbol % introduces comments that can be neglected.

The two subroutines GM_A and GM_B and other MATLAB® files for the application of the GM can be downloaded at http://www.dima.unipa.it/~petrucci/Downloads.htm

FUNCTION GM_A

FUNCTION GM_B