Abstract
Purpose
Physiological motion and partial volume effect (PVE) significantly degrade the quality of cardiac positron emission tomography (PET) images in the fast-beating hearts of rodents. Several Super-resolution (SR) techniques using a priori anatomical information have been proposed to correct motion and PVE in PET images. Ultrasound is ideally suited to capture real-time high-resolution cine images of rodent hearts. Here, we evaluated an ultrasound-based SR method using simultaneously acquired and co-registered PET-CT-Ultrafast Ultrasound Imaging (UUI) of the beating heart in closed-chest rodents.
Procedures
The method was tested with numerical and animal data (n = 2) acquired with the non-invasive hybrid imaging system PETRUS that acquires simultaneously PET, CT, and UUI.
Results
We showed that ultrasound-based SR drastically enhances the quality of PET images of the beating rodent heart. For the simulations, the deviations between expected and mean reconstructed values were 2 % after applying SR. For the experimental data, when using Ultrasound-based SR correction, contrast was improved by a factor of two, signal-to-noise ratio by 11 %, and spatial resolution by 56 % (~ 0.88 mm) with respect to static PET. As a consequence, the metabolic defect following an acute cardiac ischemia was delineated with much higher anatomical precision.
Conclusions
Our results provided a proof-of-concept that image quality of cardiac PET in fast-beating rodent hearts can be significantly improved by ultrasound-based SR, a portable low-cost technique. Improved PET imaging of the rodent heart may allow new explorations of physiological and pathological situations related with cardiac metabolism.
Similar content being viewed by others
Introduction
Standing as a paradox with respect to the vast number of applications in oncology and neurology, cardiac metabolic imaging using 2-deoxy-2-[18F]fluoro-D-glucose (FDG) positron emission tomography (PET) has so far found few clinical applications. One reason is the difficulty to attribute changes in FDG cardiac uptake to pathological versus physiological causes, e.g. substrate availability, energetic demand, and neural and hormonal regulation [1, 2]. Under basal conditions, the energetic metabolism of the normal adult heart is mostly supported by the oxidation of fatty acids. Other substrates such as lactate, ketone bodies, and glucose contribute minorly [2]. However, in conditions of increased cardiac energy demand, both physiological, e.g. strenuous exercise, and pathophysiological, e.g. acute ischemia, myocarditis, left ventricle hypertrophy, systemic hypertension, and drug toxicity, there is a switch towards glycolysis and, just as in the fetal heart, glucose becomes the preferred source of fuel of the adult heart [3,4,5,6]. PET imaging of the heart in rodent models would facilitate the exploration of the connection between the level of glucose metabolism and cardiac (patho)physiology. However, high-quality imaging of the rodent heart remains a technical challenge because of the gap between the dimensions of the heart’s movements, i.e. left ventricle displacement-velocity of around 2–3 cm/s [7,8,9,10] at 300–800 beats per minute [11], and the spatial and temporal resolutions of preclinical PET scanners, over 1 mm [12] and seconds to minutes, respectively [7]. Therefore, each cardiac PET image accumulates several heart cycles, leading to significant blurring, motion-induced artifacts, and imprecise radioactivity quantification. Gating raw PET data along the cardiac cycles synchronously with an electrocardiogram (ECG) compensates for cardiac motion (Gated Cardiac-PET [13]), but comes at the cost of lower counting statistics and contrast.
A number of methods, collectively termed super-resolution (SR), have been proposed to improve the spatial resolution of PET [14,15,16,17,18,19,20]. SR is based on iterative inverse algorithms that use a priori information from an anatomical reference in order to (i) characterize the motion vector fields (MVF) of the heart’s motion and (ii) increase spatial sampling through shifts with sub-resolution precision [15, 21, 22]. Gated Cardiac-PET frames are readily available priors for SR, but they are far from ideal due to their high noise content and low resolution [15, 22], and most SR methods use a second imaging modality, such as X-ray tomography (CT) or magnetic resonance imaging (MRI). Ultrasound is the routine reference technique for real-time, anatomical, cardiac imaging in humans and rodents, with excellent temporal (≤ 1 ms) and spatial (~ 0.1 mm) resolution, high portability, and relatively low-cost. However, to the best of our knowledge, it has never been used as prior for SR correction of cardiac PET.
Here we assessed an ultrasound-based SR technique in rodent hearts using the non-invasive in vivo preclinical imaging instrument PETRUS [9, 23] that merges simultaneously acquired and co-registered PET-CT and Ultrafast Ultrasound Imaging (UUI) [24]. Cardiac PETRUS allows the acquisition, during the same imaging session, of glucose metabolism and real-time high resolution cardiac motion with negligible effects on PET image quality [9]. This ultrasound-based SR method was applied in the image domain, and its performance was tested on simulated and real preclinical datasets.
Materials and Methods
Super-resolution in the Image Domain
SR restoration is an ill-conditioned problem since it aims to restore a high-resolution version of an object from a set of low-resolution images of it, which are related through a series of convolutional degrading steps such as motion, blurring, down-sampling, and noise corruption:
being H a high-resolution image of the inspected object, Li a set containing i = 1, …, Nf low-resolution image frames of the object, Nf is the total number of frames, Mi the MVF containing the spatio-temporal geometrical transformation of the object motion at frame i, B a blurring kernel or point spread function (PSF) of the imaging system, D a down-sampling kernel defining the difference in pixel size between H and Li, i.e. D combines several voxels of the grid into one, for example using linear decimation, and Ψi is an additive noise term characterized as a gaussian random variable with zero mean and variance σ2.
Let us define Γi : Ω → ℝ as a dataset containing low-resolution frames of a Gated Cardiac-PET, where Ω defines de image domain. Using Γi, a high-resolution original image is estimated as in [14], using a Maximum a Posteriori (MAP) variational approach [25] to minimize the functional \( F=\frac{1}{2}\sum \limits_i{\left|{\Gamma}_i-{\mathrm{L}}_i\right|}^2 \):
where \( {\hat{H}}_{\mathrm{MAP}} \) is the optimal high-resolution image that solves the variational problem of Eq. (2), TV(H) is a penalizing function that measures the quality of the restored image by countering the effect of the noise term Ψi, and λ balances the weight of the penalization term. Regarding the uptake FDG in the cardiac ventricular wall, we expect a clear difference between healthy and injured tissue but very little variation of uptake inside the healthy tissue. Hence, we adopted a Total Variation (TV) model [14] as penalizing term because it is suitable for restoring piece-wise structures and to preserve edges:
In Eq. (3), ∇ denotes the gradient operator and x is the position in the image domain. To solve the Euler-Lagrange equation associated to the variational problem of Eq. (2), we use a steepest-descent algorithm:
where Lni is a simulated set of low-resolution images that can be obtained through Eq. (1) using the high-resolution image Hn, where n = 1, …, N, defines the iterations of the algorithm, D−1 is the inverse of the down-sampling operator that performs the up-sampling of data, i.e. it divides each voxel of the grid in smaller voxels. Mi−1 inverts the MVF (we use the approximation Mi−1 = − Mi), and the deblurring kernel B−1 is the inverse of the blurring kernel B.
Ultrasound-Based Motion Registration Algorithm
The motion estimation of the myocardial during a cardiac cycle consists in performing a sequence of image-to-image registration problems between each frame at time interval i and the initial frame i = 1. We used UUI-B-mode in order to characterize the MVF, i.e. the Mi term in Eq. (1). We employed a variational approach to perform the registration of each frame by minimizing an energy functional E defined in a spatial window Υ {xj|j ϵ Υ} around the left ventricle. To account for changes of intensity that might appear in cardiac ultrasonic sequences, such as ribs’ absorption and speckle noise, we combined local and global image estimators by characterizing the local phase and intensity of the images [22]:
where ITi and IR are the image template (at frame i) and reference, respectively, and θTi and θR are the local phases of the image template and reference, respectively. δ is the Dirac function, and k is a weighting factor to balance the contribution of the intensity and local phase terms in the registration (k ≤ 1). We adopted a fluid-like regularization, which can be approximated by a Gaussian filter [26], and it was applied assuming that M is the result of the convolution of an auxiliary field m with a gaussian kernel ws of scale s:
We used a gradient descent method to minimize the functional E with respect to M:
As is often used in Demon-like registrations [27, 28], to gain stability around small values of ∇IR and ∇θR, we employed a regularized version of the gradient ∇mE as in [27, 28]:
The local phase θ(x), which does not depend on the intensity information but on the extraction of local features, e.g. points, edges, etc., can be obtained from the monogenic signal using quadrature filters [29, 30]. These filters are the combination of an even-symmetric band-pass filter (Fe, giving as result Ie = Fe ∗ I, the even component of an image I) and of two consecutive odd-symmetric filters (Fo1 and Fo2) applied to the even component of the signal:
We employ a log-Garbor radial filter as even filter and its Riesz transform as odd filters as in [31]. In order to estimate large motions, a multi-scale pyramidal refinement approach was adopted using 3 decreasing pixel size scales. Consequently, we used three center frequency for the band-pass of the log-Garbor filter as 16, 8, and 2 pixels, for each consecutive decreasing scales. At each scale, we perform 10 iterations and used additive corrections. For the fluid-like regularization (term ws in Eq. (6)), we used a Gaussian filter with a fixed scale of 10 pixels.
Implementation Details for the Ultrasound-Based SR of Cardiac PET
Figure 1 a presents the flow chart of the complete ultrasound-based SR restoration problem for cardiac-PET. The algorithm is feed with the Γi dataset of Nf low-resolution Gated Cardiac-PET images and the co-registered UUI-B-mode Nf frames (Fig. 1b). The UUI-B-mode set, which have a smaller pixel size and a better spatial resolution than the PET, is used to estimate the geometrical transformation Mi between frames (Fig. 1c). The algorithm starts with an initial high-resolution guess H1, which is the image resulting from warping and averaging the Nf Gated Cardiac-PET, up-sampled to the dimensions of the UUI-B-mode maps (Fig. 1d). As in Eq. (1), H1 is then (i) warped using each Mi, (ii) down-sampled to the dimensions of Γi, and (iii) blurred to produce Lin(Fig. 1e). The blurring kernel is the estimated PSF of the PET scanner of PETRUS, which we previously characterized [9] as a Gaussian kernel with a FWHM of 1.5 mm at the center of the field-of-view. The deblurring kernel B−1should ideally be the inverse of the blurring kernel B. However, as the PSF of a PET scanner is generally represented as a Gaussian kernel, its exact inverse would lead to an ill-posed problem. Hence, we used a simple delta-function with a width of one pixel. Several studies have shown that such simplified backward operators produce correctly reconstructed images [32,33,34]. This simplifies the term ∇HF in Eq. (4) as follows:
For all frames i, each difference Γi − Lni is up-sampled, warped-back to the selected frame of reference and averaged for all Nf. Using the current n estimation of the high-resolution image Hn, the divergence of the gradient of the TV term (last term in Eq. (4)) is calculated and the n + 1 estimation of the high-resolution image is obtained using Eq. (4). To evaluate the gradient, border elements of the image are padded by replication outside the boundaries of the image. The parameters λ and k were empirically set to 1 × 10−6 and 0.5 respectively, as they provided, respectively, a satisfying tradeoff between noise control and spatial resolution in our experiments (see “Numerical Experiments” for details about the definitions of noise and spatial resolution used), and a consisting motion registration (see supplementary material). All these steps are reiterated until the root-mean-square-error (RMSE) between estimated and measured low-resolution images varies by less than 5 % in two consecutive iterations.
Numerical Experiments
The performance of the ultrasound-based SR algorithm was tested on a numerical phantom simulating a realistic gated cardiac-PET acquisition in a numerical rat, using the ROBY phantom [12]. Assuming that respiratory and cardiac motions were perfectly cyclic, we simulated 8 respiratory frames of 0.09 s duration each, over a period of 0.72 s, which was the total length of the respiratory cycle and total length of the simulation performed, i.e. we simulated 1 respiratory cycle. For the respiratory motion, we choose 1-mm of maximum diaphragm displacement. Each simulated cardiac cycle had a duration of 0.09 s with 8 cardiac frames per respiratory frame. Input simulation images consisted in 256 × 256 × 237 voxels of 0.4 × 0.4 × 0.4 mm covering the thoracic cage of the ROBY phantom. The phantom was simulated using the Monte Carlo software MCGPU-PET [35], a fast simulator which takes into account the main relevant physical processes of the emission, transport, and detection of the radiation. The MCGPU-PET code is an adaptation of the MC-GPU software developed for X-ray imaging [36]. The libraries of cross-sections have been adapted to the 511 keV annihilation gamma rays. Two new modules have been written for the PET modality of the MC-GPU software: the photon source module that models the activity of each voxel, and the phase space detector module that tallies the location and arrival time of the photons on a cylinder around the object. MCGPU-PET allows the use of voxelized PET and CT images as input and provides different output formats including 3D-sinograms of the true and the scatter coincidences. The code selects the coincidences taking into account an energy resolution and energy window, but without including the effects of the transport of the gamma rays in the detector (i.e. it assumes a perfect detection). We used a generic preclinical scanner model, similar to the Inveon PET preclinical scanner [37], with an associated spatial resolution at the center of the scanner of ~ 1.5 mm. Each simulation was based on the specific distribution of the activity and materials of each particular frame and contained around 65 million counts, including trues and scatter coincidences. The acquired data of each frame were stored in 527 sinograms (direct and oblique), containing 129 and 168 radial and angular bins, respectively. The simulated data were reconstructed with GFIRST [38], using a 3D-OSEM algorithm and including attenuation and scatter corrections. These corrections were obtained from the known material distribution in each frame, using a 2-tissues class segmentation (air and tissue). The images were reconstructed using 128 × 128 × 127 voxels of 0.8 × 0.8 × 0.746 mm. The whole simulation and reconstructions took in total ~ 52 min with a single GPU (GeForce GTX 1080, 1.73GHz, 8Gb).
We regionally limited the SR analysis to a single 2D slice in transversal orientation. We used the phantom activity information as anatomical reference to estimate the MVF, a down-sampling factor D of one every two pixels, and a Gaussian filter with FWHM of 1.5 mm as blurring kernel B. Mean pixels’ values of regions of interest (ROIs) located in the left ventricle wall and in the ventricle’s cavity were quantified. In order to simulate a static PET acquisition, we averaged the respiratory and cardiac frames of the reconstructed PET images. To simulate a gated cardiac-PET sequence, all the respiratory frames were averaged within each phase of the cardiac cycle. As the observed effect of respiration in the simulated gated cardiac-PET was a small rigid-translation in the craniocaudal direction, a rigid registration was performed between the first frame of the reference anatomical image and the first frame of the simulated gated cardiac-PET before the registration of the cardiac phases. The estimated registration transformation was then applied to each frame of the gated cardiac-PET.
The improvement in image quality by the SR processing was assessed by measuring the signal-to-noise ratio (SNR), contrast and spatial resolution of the images. The SNR was calculated using the standard deviation (STD) and mean value (MEAN) in the ROIs:
Contrast was defined as Weber’s fraction [39] using the mean value in the left ventricle wall ROI (MEANwall) and in the cavity of the ventricle ROI (MEANcav).
Spatial resolution was defined as the lateral spread function (LSF) of the ventricle’s wall. This was evaluated as the FWHM of a Gaussian function fitted to the mirrored duplicated points, external to the edge of the ventricle’ wall, in a profile crossing the wall. The location of the external edge of the wall was extracted from the matching anatomical reference profile. The procedure was repeated on 5 intensity profiles drawn orthogonally to the heart wall, clockwise: basal lateral, mid lateral, apical, mid-septal, and basal septal [40]. Resolution was then defined as the average of the five estimated LSF.
PETRUS: Positron Emission Tomography Registered Ultrasonography
PETRUS (Fig. 2) has been described in detail in [23]. Briefly, it combines a preclinical PET-CT scanner for small animals (nanoScan Mediso Ltd., Hungary) with a clinical UUI scanner (Aixplorer, Supersonic Imagine France). The UUI component of PETRUS provides thousands of images per second, allowing the exploration of rapid phenomena with unprecedented spatial resolution (< 100 μm) [24]. Concerning cardiac studies in rats, PETRUS uses a commercial pediatric/rheumatology ultrasound probe (SuperLinear™ SLH20-6, Supersonic Imagine, France; Fig. 2b) with negligible effects on PET image quality [9]. The probe is attached through a 35-cm-long hollow carbon rectangular cuboid (Polyplan Composites, France) to a six-degree-of-freedom high-precision micromotor (Hexapod H811, Physik Instrumente, Germany; minimum incremental motion 0.2 μm) fixed to the animal bed of the PET-CT scanner. A home-made 3D-printed plastic holder joins the carbon arm and the probe. Acoustic impedance coupling between the probe and the depilated skin of the animal is obtained using degassed ultrasound gel (Medi’gel Blue ECG, Drexco Medical). The automatic process of multimodal data co-registration between UUI and PET volumes (detailed in [23]) provides a mean accuracy of co-registration of 0.10 ± 0.03 mm. In the present study, we used UUI-B-mode, typically with a plane FOV of 25.6 mm × (20 to 30) mm, a pixel-size of 0.1 mm × 0.1 mm, and 16 temporal frames covering uniformly the full heart cycle.
a Schematic flow chart of the ultrasound-based-SR method to correct cardiac PET. b Multimodal PETRUS data simultaneously acquired and co-registered. c UUI-B-mode estimated motion vector fields of the heart’s deformation. d The initial high-resolution (HR) guess image used in the ultrasound-based SR is the up-sampling of the result of registering and averaging all the low-resolution (LR) gated PET frames. e Using Eq. (1), the HR image simulates LR frames. f An averaged correction for the current HR image is calculated using Eq. (4) and regularized using TV, providing the HR image obtained at iterative step n of the algorithm. g Final ultrasound-based SR image.
To obtain the ultrasound B-mode images, we employ the research mode of our ultrafast scanner. We performed 500 frames-per-second (fps) acquisition employing flat research acquisition mode, spatial compounding using 5 beams orientation at − 6, − 3, 0, 3, and 6 degrees, and 15 MHz of central frequency. Spatial compounding is a classical method for speckle noise reduction that have demonstrated to avoid excessive speckle reduction. Besides, we combined this method with another classical image regularization aiming as well to improve image quality by noise speckle reduction consisting in post-filtering with Laplacian pyramid-based nonlinear diffusion, in which nonlinear diffusion filtering is applied to band-pass ultrasound images in using a multi-scale, Laplacian domain [41]. The total effect of the regularization employed is a set of images with reduced granularity and enhanced edges suitable for motion detection [42].
Animal Experiments
Animal experiments were approved by the French Ethical Committee (approval number 18–146). We processed real data acquired with the PETRUS system from two successive imaging sessions of a 10-week-old female Wistar rat: (i) in normal conditions (baseline) and (ii) after surgically induced myocardial infarction. Baseline imaging was done 3 days before surgery. During surgery, the rat was under isoflurane anesthesia (2.5 %), and physiological parameters were constantly monitored. Analgesics were injected before and post-surgery. A permanent ligation of the left anterior descending coronary artery (LADCA) was performed after thoracotomy under endotracheal intubation. The incision was sutured, and the air in the thorax removed. The rat was imaged 4 h after LADCA ligation. For both imaging sessions, the rat was positioned on a customized bed (as in Fig. 2b) with ECG, temperature, and respiration monitoring. For the baseline and the infarcted cases, the mean registered animal’s heart rate was 260 and 277 beats per minute (bpm), respectively. We used a high level of isoflurane during imaging (~ 4 %) in order to limit the respiratory rate and minimize the effect of respiratory motion on PET acquisitions. The ultrasound probe was positioned over the chest to obtain a standard long-axis view of the myocardium with UUI-B-mode at a frame rate 500 fps for 5 s. UUI-B-mode acquisitions were triggered at the respiratory pause of the animal. A CT scan was acquired for attenuation correction of the PET data in semi-circular mode, with 50 kV, 720 projections, and 170 ms per projection. Attenuation correction was based on default settings of the PET-CT scanner using two tissues segmentation (tissue and air). Gated acquisition was started 30 min after the injection of 400 μL of ~ 41 MBq FDG in 0.9 % NaCl. The 30-min ECG-gated PET acquisition and UUI-B-mode were acquired simultaneously. From the sequence acquired with UUI-B-mode, a full cardiac cycle in respiratory pause was extracted using the simultaneously acquired ECG and respiratory signals. Next, the extracted frames were interpolated to 16 frames uniformly spaced in time. Every gated cardiac-PET image was reconstructed after removing heart cycles longer or shorter than 40 % of the mean nominal heart cycle duration along the whole experiment. PET data were reconstructed using the Tera-Tomo reconstruction engine (Mediso, Hungary) with 6 iterations and 4 subsets, scatter and attenuation correction, and with 16 temporal frames, covering the full cardiac cycle. Finally, the multimodal PETRUS data was co-registered. Long-axis view was chosen in order to explore the territory irrigated by the LADCA.
Results
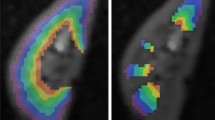
Regarding the simulated experiments, Fig. 3 summarizes the results of this test and shows the reference end-diastole cardiac phase, the gated-PET in end-diastole cardiac phase, the static-PET, and the anatomy-based SR image. Compared with the ground-truth image, image quality of the gated-PET and static-PET images is notably degraded. The definition of the structure of the wall is partially lost as well as the quantitative information. However, both the MoCo and SR image are qualitatively and quantitatively improved in that respect. Quantification of the selected ROIs are reported in Table 1.
Numerical test using PET simulated data with the realistic rat phantom including both respiratory and cardiac modeling (ROBY) and the Monte Carlo software MCGPU-PET. a Ground-truth distribution of activity. b Gated PET image in end-diastole cardiac phase. c Static PET reconstruction. d Anatomy-based motion correction (MoCo). e Anatomy-based SR reconstruction. Asterisk (*) indicates that both images were obtained using as anatomic reference the real phantom activity distribution.
We observed that the deviations between the mean intensity values in the evaluated ROIs and their expected values were smaller in the ROIs located in the ventricle’s wall than the ones located inside the ventricle’s cavity (Table 1). This is expected because inside the cavity the PET signal is considerable smaller than in the tissue and because this region does not present tissue in motion that could be used to increase the spatial sampling.
In the ventricle’s wall, the smaller deviations between mean and expected values in the ROIs were obtained for the SR images (2 %), followed by the gated- PET (7 %), the MoCo (11 %), and the static-PET images (12 %). However, the image quality of the frames of the gated-PET was very low (see Fig. 3), preventing their diagnostic function and reliability. The deviations between expected and mean values were improved in a 7 % after applying MoCo and in an 82 % after applying SR in comparison with the static PET. Taking the MoCo images as reference, the SR treatment provided 81 % more reliable quantitative values than MoCo ones.
In terms of image quality parameters, using the static-PET images as reference, we observed an improvement of 4 % in terms of contrast, of 23 % in terms of SNR, and 13 % in terms of spatial resolution of the MoCo images, while in the SR image these values improved in 66 %, 41 %, and 55 % for the contrast, SNR, and spatial resolution, respectively. Taking the MoCo as reference, the SR images provides 60 %, 14 %, and 48 % better values of contrast, SNR, and spatial resolution, respectively.
Regarding the in vivo experiments, Fig. 4 shows the motion vector fields between diastole and systole cardiac phases for the intact and ischemic hearts. The overall motion seems to be correctly identified, and the mechanical affectation of the ischemic heart can be well appreciated. Figure 5 shows in end-diastole cardiac phase, UUI-B-mode, gated PET, MoCo, ultrasound-based SR, and static PET images, in intact and infarcted rat hearts. Table 1 reports the quantification performed over those images. Qualitatively, in the MoCo and ultrasound-based SR images, the FDG uptake sharply delineated the walls of the left ventricle. However, the ultrasound-based SR images present less spillover outside ventricle’s wall tissues. Additionally, the ultrasound-based SR image clearly identified the metabolic remodeling in the ischemic myocardium corresponding to the vascular territory of the ligated LADCA, evidencing a small but still active FDG uptake in the ischemic region that could not be properly appreciated in the rest of available images.
Multimodal PETRUS images of an intact (a–e) and 4-h post left-descending coronary artery ligation (f–j) rat heart. a, f UUI-B-mode image in long-axis orientation and end-diastole phase. b, g Static PET images. c, h Ultrasound-based MoCo images. d, i Gated PET in end-diastole frame. e, j Ultrasound-based SR images. The black arrow in j points towards the ischemic area.
Taking the static-PET images as reference, the mean values in the ROIs increased by 4 % in the intact ventricle’s wall and by 13 % in the ischemic region when MoCo was applied, and by 28 % and 40 % in the intact ventricle’s wall and in the ischemic region, respectively, when ultrasound-based SR was applied. Using as reference the MoCo images, the ultrasound-based SR provided 32 % and 40 % higher SUV values in the ventricle’s wall and in the ischemic region, respectively. Compared to those of the static images MoCo provided a modest improvement of the image quality parameters, 3 %, 5 %, and 5 % for the contrast, SNR, and spatial resolution, respectively. However, utrasound-based SR yielded 102 %, 11 %, and 56 % higher contrast, SNR, and spatial resolution, respectively, than static PET images. Comparing MoCo and ultrasound-based SR images, the latter provided 95 %, 5 %, and 54 % better contrast, SNR, and spatial resolution, respectively, than the former. Overall, ultrasound-based SR yielded submillimetric spatial resolution with an average value of 0.88 mm.
Discussion
The previous results support the hypothesis that ultrasound-based SR improves the spatial resolution of the images without affecting the SNR, which is a basic precept of the technique. Analogously, all the image quality parameters evaluated were considerably improved, facilitating the identification of heart lesions, which appear enhanced in the images as a result of a better spatial resolution and decreased PVE. The total amount of counts present in the entire gated-PET sequence (2.35 × 1010 and 2.63 × 1010counts for the intact and infarcted hearts, respectively) were not substantially modified by the ultrasound-based SR algorithm (2.35×1010counts and 2.65 ×1010counts for the intact and infarcted heart). Importantly, the ultrasound image acquisition is performed during the PET acquisition and provides images in real time. Co-registration of multimodal data takes 2 min on a dual core Intel(R) Xeon(R) CPU E-5-2637 v4 @ 3.5GHz, and most of this time is used for data loading of the PET volumes. Ultrasound-based SR adds a short computation time to the reconstruction process. The motion registration of 16 UUI-B-mode frames takes 1 min, and the SR algorithm 1 min on the same machine. Both codes were run in non-parallelized conditions, while parallelization is likely to improve considerably the execution time.
In this study we used gated-PET reconstructions of 16 frames/cycle associated to 16 UUI-B-mode anatomical frames/cycle. The reconstruction time for a 30-min acquisition using 16 gates and the commercial software of MEDISO run on the dedicated workstation is ~ 5.5 h, and ~ 10.4 h for 32 gates. The SNR from 16 to 32 gates, using as example the intact heart rat examination described in “Animal Experiments,” decreased in ~ 40 %, leading to a considerable loss of signal. Therefore, in the present configuration there is no advantage to explore much higher frame rates even if they are compatible with UUI, if onr is to keep reasonable reconstruction times and good PET image quality.
One limitation of the present study is that our PET-CT scanner did not allow to double trigger PET data acquisition. Hence, we used a high level of isoflurane (~ 4 %) in order to limit the respiratory rate and minimize the effect of respiratory motion on PET acquisitions. In these conditions, the observed cardiac displacement due to respiration estimated from the B-mode image was ~ 0.7 mm, which is smaller than our PET’s spatial resolution. Additionally, it is noteworthy that, in spite of the simplicity provided by in-image-domain SR, reconstruction-incorporated SR methods have also been reported as in [43] and may represent a future extension of the present study.
The SR method developed in this work uses 2D ultrasonic sequences, while the beating heart undergoes complex movements in 3D. However, the rapid progresses of 3D ultrasound probes, some of which are already in exploitation in clinical and preclinical practice, will allow 3D SR in the near future [44]. Moreover, the use of MVF in 3D obtained from ultrasound may indeed be a convenient methodology to create 4D virtual X-rays CTs to provide attenuation correction in PET images [22].
A particularity of this study is that it requires a temporal framing to sample the cardiac cycle superior to the one employed in classical echocardiography. Dedicated clinical echocardiography systems provide sequences allowing up to 50–80 fps, which is sufficient to image the resting heart beating (in humans is ~ 70 bpm) [45]. However, to perform stress echocardiography or preclinical imagining, such temporal framing results insufficient to sample the heart cycle [45]. Therefore, other imaging schemes to increase frame rate while keeping high image quality are needed, such as cardiac-UUI (the technique employed in this study) or multi-line transmit technique [24, 46]. In particular, UUI technology offers a large diversity of functional imaging information such as the measurement of cardiac contraction parameters and myocardial elasticity [23, 24], which could be used in combination with high-resolution metabolic imaging of the heart.
Conclusions
We presented the proof-of-concept that ultrasound-based SR techniques based on co-registered, simultaneously acquired PET and ultrasonic data drastically enhance the quality of metabolic images of the rodent heart in terms of spatial resolution, SNR, and contrast. The performance of the method was demonstrated using numerical and animal data. In the infarcted rat heart, ultrasound-based SR improved the delineation of the metabolic defect due to the post-ischemic lesion. Ultrasound-based SR cardiac-PET allows precise imaging of cardiac metabolism in pathological situations characterized by cardiac glucose dysregulation.
References
Jeppesen J, Kiens B (2012) Regulation and limitations to fatty acid oxidation during exercise. J Physiol Lond 590(5):1059–1068
Pascual F, Coleman RA (2016) Fuel availability and fate in cardiac metabolism: a tale of two substrates. Biochimica Et Biophysica Acta (BBA)-Molecular and Cell Biology of Lipids 1861(10):1425–1433
J. Sourdon, F. Lager, T. Viel, D. Balvay, R. Moorhouse, E. Bennana, G. Renault, P. L. Tharaux, N. Dhaun and B. Tavitian, "Cardiac metabolic deregulation induced by the tyrosine kinase receptor inhibitor sunitinib is rescued by endothelin receptor antagonism," Theranostics, vol. 7, (11), pp. 2757–2774, Jul 8, 2017
Haas F, Jennen L, Heinzmann U, Augustin N, Wottke M, Schwaiger M, Lange R (2001) Ischemically compromised myocardium displays different time-courses of functional recovery: correlation with morphological alterations? Eur J Cardiothorac Surg 20(2):290–298
Vesely MR, Dilsizian V (2008) Nuclear cardiac stress testing in the era of molecular medicine. J Nucl Med 49(3):399–413
Hernández-Esquivel L, Marín-Hernández A, Pavón N, Carvajal K, Moreno-Sánchez R (2006) Cardiotoxicity of copper-based antineoplastic drugs casiopeinas is related to inhibition of energy metabolism. Toxicol Appl Pharmacol 212(1):79–88
Moses WW (2011) Fundamental limits of spatial resolution in PET. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 648:S236–S240
Luo J, Konofagou EE (2011) Imaging of wall motion coupled with blood flow velocity in the heart and vessels in vivo: a feasibility study. Ultrasound Med Biol 37(6):980–995
Perez-Liva M, Viel T, Yoganathan T, Garofalakis A, Sourdon J, Facchin C, Tanter M, Provost J, Tavitian B (2018) Performance evaluation of the PET component of a hybrid PET/CT-ultrafast ultrasound imaging instrument. Phys Med Biol 63(19):19NT01
Visser EP, Disselhorst JA, Brom M, Laverman P, Gotthardt M, Oyen WJ, Boerman OC (2009) Spatial resolution and sensitivity of the Inveon small-animal PET scanner. J Nucl Med 50(1):139–147
Website: "Animal Care and Use Johns Hopkins University," [online] http://web.jhu.edu/animalcare/procedures/mouse.html. Accessed on 12/10/2019
Segars WP, Tsui BM, Frey EC, Johnson GA, Berr SS (2004) Development of a 4-D digital mouse phantom for molecular imaging research. Mol Imaging Biol 6(3):149–159
Lang N, Dawood M, Büther F, Schober O, Schäfers M, Schäfers K (2006) Organ movement reduction in PET/CT using dual-gated listmode acquisition. Z Med Phys 16(1):93–100
Marquina A, Osher SJ (2008) Image super-resolution by TV-regularization and Bregman iteration. J Sci Comput 37(3):367–382
Ahn IJ, Kim JH, Chang Y, Nam WH, Ra JB (2016) Super-resolution reconstruction of 3d pet images using two respiratory-phase low-dose ct images. IEEE Transactions on Radiation and Plasma Medical Sciences 1(1):46–55
Kennedy JA, Israel O, Frenkel A, Bar-Shalom R, Azhari H (2006) Super-resolution in PET imaging. IEEE Trans Med Imaging 25(2):137–147
S. Ambwani, W. C. Karl, A. Tawakol and H. Pien, "Joint cardiac and respiratory motion correction and super-resolution reconstruction in coronary PET/CT," in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2011, pp. 1702-1705
J. L. Rubio-Guivernau, M. J. Ledesma-Carbayo, F. Lamare, J. E. Ortuno, P. Guerra, D. Visvikis, A. Santos and G. Kontaxakis, (2007)"Respiratory motion correction in PET with super-resolution techniques and non-rigid registration," in 2007 IEEE Nuclear Science Symposium Conference Record, pp. 3560–3563
H. Yan, F. Gigengack, X. Jiang and K. Schäfers, (2013)"Super-resolution in cardiac PET using mass-preserving image registration," in 2013 IEEE International Conference on Image Processing, , pp. 752–756
Wallach D, Lamare F, Kontaxakis G, Visvikis D (2011) Super-resolution in respiratory synchronized positron emission tomography. IEEE Trans Med Imaging 31(2):438–448
Küstner T, Schwartz M, Martirosian P, Gatidis S, Seith F, Gilliam C, Blu T, Fayad H, Visvikis D, Schick F (2017) MR-based respiratory and cardiac motion correction for PET imaging. Med Image Anal 42:129–144
Nam WH, Ahn IJ, Kim KM, Kim BI, Ra JB (2013) Motion-compensated PET image reconstruction with respiratory-matched attenuation correction using two low-dose inhale and exhale CT images. Phys Med Biol 58(20):7355
Provost J, Garofalakis A, Sourdon J, Bouda D, Berthon B, Viel T, Perez-Liva M, Lussey-Lepoutre C, Favier J, Correia M (2018) Simultaneous positron emission tomography and ultrafast ultrasound for hybrid molecular, anatomical and functional imaging. Nature Biomedical Engineering 2(2):85
Tanter M, Fink M (2014) Ultrafast imaging in biomedical ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control 61(1):102–119
Rudin LI, Osher S, Fatemi E (1992) Nonlinear total variation based noise removal algorithms. Physica D 60(1):259–268
O. Somphone, M. De Craene, R. Ardon, B. Mory, P. Allain, H. Gao, J. D'hooge, S. Marchesseau, M. Sermesant and H. Delingette, "Fast myocardial motion and strain estimation in 3D cardiac ultrasound with sparse demons," in 2013 IEEE 10th International Symposium on Biomedical Imaging, 2013, pp. 1182–1185
A. Tristán-Vega, G. Vegas-Sánchez-Ferrero and S. Aja-Fernández, "Local similarity measures for demons-like registration algorithms," in 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2008, pp. 1087–1090
Thirion J (1998) Image matching as a diffusion process: an analogy with Maxwell's demons. Med Image Anal 2(3):243–260
Felsberg M, Sommer G (2001) The monogenic signal. IEEE Trans Signal Process 49(12):3136–3144
Mellor M, Brady M (2005) Phase mutual information as a similarity measure for registration. Med Image Anal 9(4):330–343
Bridge CP (2017) Introduction to the monogenic signal. arXiv Preprint arXiv 1703:09199
Cal-González J, Pérez-Liva M, Herraiz JL, Vaquero JJ, Desco M, Udías JM (2015) Tissue-dependent and spatially-variant positron range correction in 3D PET. Medical Imaging, IEEE Transactions On 34(11):2394–2403
Zeng GL, Gullberg G, Tsui B, Terry J (1991) Three-dimensional iterative reconstruction algorithms with attenuation and geometric point response correction. IEEE Trans Nucl Sci 38(2):693–702
Zeng GL, Gullberg GT (2000) Unmatched projector/backprojector pairs in an iterative reconstruction algorithm. IEEE Trans Med Imaging 19(5):548–555
A. Badal, J. Domarco, J. M. Udias and J. L. Herraiz,(2018) "MCGPU-PET: a real-time Monte Carlo PET simulator," in International Symposium on Biomedical Imaging, Washington, DC,,
Badal A, Badano A (2009) Accelerating Monte Carlo simulations of photon transport in a voxelized geometry using a massively parallel graphics processing unit. Med Phys 36(11):4878–4880
Constantinescu CC, Mukherjee J (2009) Performance evaluation of an Inveon PET preclinical scanner. Phys Med Biol 54(9):2885
Herraiz J, España S, Cabido R, Montemayor A, Desco M, Vaquero JJ, Udías JM (2011) GPU-based fast iterative reconstruction of fully 3-D PET sinograms. IEEE Trans Nucl Sci 58(5):2257–2263
Peli E (1990) Contrast in complex images. Josa A 7(10):2032–2040
Schiller NB (1991) Two-dimensional echocardiographic determination of left ventricular volume, systolic function, and mass. Summary and discussion of the 1989 recommendations of the American Society of Echocardiography. Circulation 84(3 Suppl):I280–I287
Park J, Kang JB, Chang JH, Yoo Y (2014) Speckle reduction techniques in medical ultrasound imaging. Biomed Eng Lett 4(1):32–40
De Luca V, Székely G, Tanner C (2015) Estimation of large-scale organ motion in B-mode ultrasound image sequences: a survey. Ultrasound Med Biol 41(12):3044–3062
D. Wallach, F. Lamare, C. Roux and D. Visvikis, "Comparison between reconstruction-incorporated super-resolution and super-resolution as a post-processing step for motion correction in PET," in IEEE Nuclear Science Symposuim & Medical Imaging Conference, 2010, pp. 2294–2297
Q. Huang and Z. Zeng,2017 "A review on real-time 3D ultrasound imaging technology," BioMed Research International, vol 2017,
Joos P, Porée J, Liebgott H, Vray D, Baudet M, Faurie J, Tournoux F, Cloutier G, Nicolas B, Garcia D (2018) High-frame-rate speckle-tracking echocardiography. IEEE Trans Ultrason Ferroelectr Freq Control 65(5):720–728
R. Mallart and M. Fink, "Improved imaging rate through simultaneous transmission of several ultrasound beams," in New Developments in Ultrasonic Transducers and Transducer Systems, 1992, pp. 120–130
Funding
This study was supported by France Life Imaging grant ANR-11-INBS-0006 and partly by Plan Cancer Physicancer program BIMUPET (C16025KS). In vivo imaging was performed at the Life Imaging Facility of Paris Descartes University (Plateforme Imageries du Vivant), supported by France Life Imaging (grant ANR-11-INBS-0006) and Infrastructures Biologie-Santé.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic Supplementary Material
ESM 1
(DOCX 517 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Perez-Liva, M., Yoganathan, T., Herraiz, J.L. et al. Ultrafast Ultrasound Imaging for Super-Resolution Preclinical Cardiac PET. Mol Imaging Biol 22, 1342–1352 (2020). https://doi.org/10.1007/s11307-020-01512-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11307-020-01512-w