Abstract
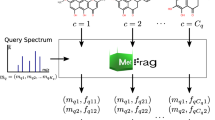
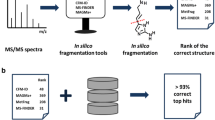
Electrospray tandem mass spectrometry (ESI-MS/MS) is commonly used in high throughput metabolomics. One of the key obstacles to the effective use of this technology is the difficulty in interpreting measured spectra to accurately and efficiently identify metabolites. Traditional methods for automated metabolite identification compare the target MS or MS/MS spectrum to the spectra in a reference database, ranking candidates based on the closeness of the match. However the limited coverage of available databases has led to an interest in computational methods for predicting reference MS/MS spectra from chemical structures. This work proposes a probabilistic generative model for the MS/MS fragmentation process, which we call competitive fragmentation modeling (CFM), and a machine learning approach for learning parameters for this model from MS/MS data. We show that CFM can be used in both a MS/MS spectrum prediction task (ie, predicting the mass spectrum from a chemical structure), and in a putative metabolite identification task (ranking possible structures for a target MS/MS spectrum). In the MS/MS spectrum prediction task, CFM shows significantly improved performance when compared to a full enumeration of all peaks corresponding to substructures of the molecule. In the metabolite identification task, CFM obtains substantially better rankings for the correct candidate than existing methods (MetFrag and FingerID) on tripeptide and metabolite data, when querying PubChem or KEGG for candidate structures of similar mass.






Similar content being viewed by others
Notes
Although mass spectrometry measures mass over charge, we assume charge is always 1 (see Assumption 1 in Sect. 2.1.1) and hence can use the mass here.
References
Böcker, S., & Rasche, F. (2008). Towards de novo identification of metabolites by analyzing tandem mass spectra. Bioinformatics, 24(16), i49–i55.
Bolton, E., Wang, Y., Thiessen, P., & Bryant, S. (2008). PubChem: Integrated platform of small molecules and biological activities. In Chapeter 12 in Annual reports in computational chemistry (Vol. 4). Washington, DC: American Chemical Society.
Cappé, O., Moulines, E., & Ryden, T. (2005). Inference in hidden Markov models. Berlin: Springer.
de Hoffman, E., & Stroobant, V. (2007). Mass spectrometry: Principles and applications (3rd ed.). Chichester: Wiley.
Deming, S., & Stephan, W. (1940). On a least squares adjustment of a sampled frequency table when the expected marginal totals are known. Annals of Mathematical Statistics, 11(4), 427–444.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B (Methodological), 39(1), 1–38.
Dunn, W. B., & Ellis, D. I. (2005). Metabolomics: Current analytical platforms and methodologies. Trends in Anal Chem, 24(4), 285–294.
Eng, J. K., McCormack, A. L., & Yates, J. R. (1994). An approach to correlate Tandem mass spectral data of peptides with amino acid sequences in a protein database. Journal of the American Society for Mass Spectrometry, 5(11), 976–989.
Fiehn, O. (2002). Metabolomics-the link between genotypes and phenotypes. Plant Molecular Biology, 48(1–2), 155–171.
Galezowska, A., Harrison, M. W., Herniman, J. M., Skylaris, C. K., & Langley, G. J. (2013). A predictive science approach to aid understanding of electrospray ionisation tandem mass spectrometric fragmentation pathways of small molecules using density functional calculations. Rapid Communications in Mass Spectrometry (RCM), 27(9), 964–970.
Gasteiger, J., & Marsili, M. (1980). Iterative partial equalization of orbital electronegativity: A rapid access to atomic charges. Tetrahedron, 36(22), 3219–3228.
Gasteiger, J., Haneback, W., & Schulz, K. P. (1992). Prediction of mass spectra from structural information. Journal of Chemical Information and Computer Sciences, 32, 264–271.
Hastings, J., de Matos, P., & Dekker, A. (2013). The ChEBI reference database and ontology for biologically relevant chemistry: Enhancements for 2013. Nucleic Acids Research, 41(Database issue), D456–D463.
Heinonen, M., Rantanen, A., Mielikainen, T., et al. (2008). FiD: a software for ab initio structural identification of product ions from tandem mass spectrometric data. Rapid Communications in Mass Spectrometry, 22, 3043–3052.
Heinonen, M., Shen, H., Zamboni, N., & Rousu, J. (2012). Metabolite identification and molecular fingerprint prediction through machine learning. Bioinformatics, 28(18), 2333–2341.
Hill, A. W., & Mortishire-Smith, R. J. (2005). Automated assignment of high-resolution collisionally activated dissociation mass spectra using a systematic bond disconnection approach. Rapid Communications in Mass Spectrometry, 19(21), 3111–3118.
Horai, H., Arita, M., Kanaya, S., et al. (2010). MassBank: A public repository for sharing mass spectral data for life sciences. Journal of Mass Spectrometry, 45(7), 703–714.
Hufsky, F., Scheubert, K., & Böcker, S. (2014). Computational mass spectrometry for small-molecule fragmentation. Trends in Analytical Chemistry, 53, 41–48.
Kanehisa, M., Goto, S., Hattori, M., et al. (2006). From genomics to chemical genomics: New developments in KEGG. Nucleic Acids Research, 34, D354–D357.
Kangas, L. J., Metz, T. O., Isaac, G., Schrom, B. T., Ginovska-Pangovska, B., Wang, L., et al. (2012). In silico identification software (ISIS): A machine learning approach to tandem mass spectral identification of lipids. Bioinformatics, 28(13), 1705–1713.
Katajamaa, M., & Oresic, M. (2007). Data processing for mass spectrometry-based metabolomics. Journal of Chromatography A, 1158(1–2), 318–328.
Kerber, A., Meringer, M., & Rücker, C. (2006). CASE via MS: Ranking structure candidates by mass spectra. Croatica Chemica Acta, 79(3), 449–464.
Kind, T., & Fiehn, O. (2010). Advances in structure elucidation of small molecules using mass spectrometry. Bioanalytical Reviews, 2(1–4), 23–60.
Koller, D., & Friedman, N. (2009). Probabilistic graphical models: Principles and techniques. Cambridge: The MIT Press.
Levsen, K., Schiebel, H. M., et al. (2007). Even-electron ions: A systematic study of the neutral species lost in the dissociation of quasi-molecular ions. Journal of Mass Spectrometry (JMS), 42, 1024–1044.
Lindsay, R. K., Buchanan, B. G., Feigenbaum, E. A., & Lederberg, J. (1980). Applications of artificial intelligence for organic chemistry: The DENDRAL project. New York: McGraw-Hill Book Company.
Ma, B., Zhang, K., Hendrie, C., Liang, C., et al. (2003). PEAKS: Powerful software for peptide de novo sequencing by tandem mass spectrometry. Rapid Communications in Mass Spectrometry, 17(20), 2337–2342.
McLafferty, F. W., & Turecek, F. (1993). Interpretation of Mass Spectra (4th ed.). Mill Valley: University Science Books.
Mylonas, R., Mauron, Y., Masselot, A., et al. (2009). X-Rank: A robust algorithm for small molecule identification using tandem mass spectrometry. Analytical Chemistry, 81(18), 7604–7610.
Oberacher, H., Pavlic, M., Libiseller, K., et al. (2009). On the inter-instrument and the inter-laboratory transferability of a tandem mass spectral reference library: 2. Optimization and characterization of the search algorithm. Journal of Mass Spectrometry (JMS), 44(4), 494–502.
Paizs, B., & Suhai, S. (2005). Fragmentation pathways of protonated peptides. Mass Spectrometry Reviews, 24(4), 508–548.
Papayannopoulos, I. (1995). The interpretation of collision-induced dissociation tandem mass spectra of peptides. Mass Spectrometry Reviews, 14(April), 49–73.
Perkins, D. N., Pappin, D. J. C., Creasy, D. M., & Cottrell, J. S. (1999). Probability-based protein identification by searching sequence databases using mass spectrometry data. Electrophoresis, 20, 3551–3567.
Scheubert, K., Hufsky, F., & Böcker, S. (2013). Computational mass spectrometry for small molecules. Journal of Cheminformatics, 5(1), 12.
Smith, C. A., O’Maille, G., Want, E. J., et al. (2005). METLIN: A metabolite mass spectral database. Therapeutic Drug Monitoring, 27(6), 747–751.
Stein, S. E., & Scott, D. R. (1994). Optimization and testing of mass spectral library search algorithms for compound identification. Journal of the American Society for Mass Spectrometry, 5(9), 859–866.
Sumner, L. W., Amberg, A., Barrett, D., et al. (2007). Proposed minimum reporting standards for chemical analysis. Metabolomics, 3, 211–221.
Tautenhahn, R., Cho, K., Uritboonthai, W., et al. (2012). An accelerated workflow for untargeted metabolomics using the METLIN database. Nature Biotechnology, 30(9), 826–828.
Wishart, D. S. (2011). Advances in metabolite identification. Bioanalysis, 3(15), 1769–1782.
Wishart, D. S., Knox, C., Guo, A. C., et al. (2009). HMDB: A knowledgebase for the human metabolome. Nucleic Acids Research, 37, D603–D610.
Wishart, D. S., Jewison, T., Guo, A. C., et al. (2013). HMDB 3.0: The Human Metabolome Database in 2013. Nucleic Acids Research, 41, D801–D807.
Wolf, S., Schmidt, S., Müller-Hannemann, M., & Neumann, S. (2010). In silico fragmentation for computer assisted identification of metabolite mass spectra. BMC Bioinformatics, 11, 148.
Acknowledgments
Many thanks to Dale Schuurmans, Liang Li, and Jun Peng at the University of Alberta, as well as to the Steinbeck Group at the European Bioinformatics Institute (EMBL-EBI), for invaluable discussions and advice. This work was supported by the Natural Sciences and Engineering Research Council of Canada; Alberta Innovates Technology Futures; and Alberta Innovates Health Solutions and made possible by the Compute Canada Westgrid facility.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Allen, F., Greiner, R. & Wishart, D. Competitive fragmentation modeling of ESI-MS/MS spectra for putative metabolite identification. Metabolomics 11, 98–110 (2015). https://doi.org/10.1007/s11306-014-0676-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11306-014-0676-4