Introduction

In breeding programs, genetic improvement depends on a reliable estimation of genetic parameters as heritability, genetic correlations and breeding values. Conventional tree breeding programs use phenotype information provided by progeny testing, together with pedigree records to obtain estimations of these parameters. Open-pollination is one of the most frequently used mating designs, since its simplicity and low cost allow to evaluate the genetic merit of a large number of trees. Thus, genetic parameters are estimated by applying a model that assumes a complete outcrossing mating, where open-pollinated families are represented as half-sibs. However, the presence of offspring from parents related to each other or with both parents in common (full siblings) establishes new types of relationships that are not considered by the pedigree in open-pollinated families (Namkoong 1965). In addition, selfing is frequent in Eucalyptus species and, since it is not documented in the pedigree, it affects the estimation of genetic parameters and breeding values, and therefore the selection of superior trees (Squillace 1974; Bush et al. 2011). The errors of relatedness among and within families, generated by pedigree mistakes or simply by having incomplete pedigrees, as well as the presence of selfings, can be corrected using genomic information (Muñoz et al. 2014; Mphahlele et al. 2020).

Eucalyptus species show predominantly outcrossing mating systems though there is also a considerable degree of self-fertilization, with selfing rates ranging between 0.04 and 0.55 (Eldridge et al. 1993). For Eucalyptus globulus Labill., a mean selfing rate of 0.40 has been reported, with a range of 0.05 to 0.87, associated with individual tree variation and flowering density (Patterson et al. 2004). Ignoring the mixed-mating system, with both selfing and outcrossing, is one of major sources of error in the estimation of genetic parameters, inflating genetic variances estimates, and consequently the heritability (Eldridge et al. 1993). To consider the existence of self-fertilization in open-pollinated populations, in estimating the heritability in Eucalyptus, a kinship coefficient greater than 1/4 is generally used, typically 1/3 or 1/2.5 (Squillace 1974). Although the proposed adjustment is based on a rate of selfing of 30%, in most populations the actual value is unknown (Volker et al. 1990). In addition, this correction only avoids the overestimation of the additive variance and heritability, but has no impact on individual breeding values.

Currently the animal model, referred to as an individual tree mixed model when applied in forest tree breeding, is the approach generally used for the estimation of genetic parameters and the prediction of breeding values (Balmelli et al. 2013; Cappa et al. 2016). The main advantage of this model is the simultaneous estimation of breeding values for parents and progeny. In this approach, an average numerator relationship matrix (A) is used to indicate the additive covariance between all individuals, taking values of 0.5 between parent-offspring and 0.25 for half-sibs of an open-pollinated population. This matrix also allows the easy incorporation of higher levels of relatedness based on pedigree information. Dutkowski et al. (2001) developed an adjustment to include the selfing effect in this matrix, resulting in an increased level of relatedness in the population. Simulation studies that incorporated this A modified matrix with the specific populational selfing rate in the individual tree model approach resulted in less biased estimates of variance components and breeding values (Dutkowski et al. 2001). However, the application and further evaluation of this methodology on real breeding populations are limited by the lack of knowledge of the selfing rate.

The development of high-throughput genotyping technologies has provided genetic information distributed throughout the genome. The availability of genome-wide molecular markers for several forest tree species, such as Eucalyptus, Pinus, and Populus, enables to predict genomic breeding value to implement new breeding strategies, such as genomic selection (Meuwissen et al. 2001). The Genomic Best Linear Unbiased Prediction (GBLUP) includes a genomic relationship matrix (G) derived from markers in a mixed model approach for estimation of genomic breeding values (VanRaden 2008). This matrix accurately estimates the genetic similarity, enabling to account for the actual proportion of genome share among individuals and the variation due to Mendelian segregation (Visscher et al. 2006). The application of GBLUP can be a notably valuable tool in forest tree breeding programs to overcome one of its main challenges, the detection of unknown relationships, so improving the accuracy of genetic parameters and breeding values estimation and, therefore, increasing the selection efficiency (Tan et al. 2017; Ukrainetz and Mansfield 2020).

Nowadays, the genomic selection approach has been expanded to include pedigree and genomic information in a single unified model, which has been proposed by Aguilar et al. (2010), Christensen and Lund (2010), and Legarra et al. (2009), and is known as single-step evaluation. Since one of the problems faced by forest tree breeding programs is the high cost of genotyping, this method allows the phenotypic and pedigree data of the entire breeding program to be incorporated in the same analysis with the genotypic information of a subset of the population. Different methods to calculate the genomic relationships have been tested to improve the adjustment of this matrix to the pedigree-based relationship matrix and compared the accuracies of predictions (Forni et al. 2011; Vitezica et al. 2011). However, for species with mixed-mating systems as Eucalyptus, the average numerator relationship matrix can be affected by shallow pedigree structures, due to, for example, cryptic relatedness and presence of selfings. Thus, modifications of the pedigree-based relationship matrix to complete pedigree information and integrate selfing rate, as well as the effects on accuracy of breeding values predicted by single-step evaluations, remain to be assessed.

Therefore, using data from a breeding population of E. globulus, the objectives of this study were (a) to compare the precision of breeding values predicted with the conventional pedigree-based model and with the pedigree-genomic single-step model and (b) to estimate the population’s selfing rate and test the predictive ability of both approaches when the selfing rate is incorporated into the analysis.

Materials and methods

Breeding population and phenotyping

The E. globulus population belongs to the breeding program of the Instituto Nacional de Investigación Agropecuaria (INIA) of Uruguay. The population comprises two generations of breeding. The first generation includes materials from Australia and Chile, and selections from Uruguayan commercial plantations. The second generation was formed by the recombination of the first-generation individuals by open-pollination. A progeny test with 194 families from both generations was installed in Lavalleja (latitude 34∘ 110 S; longitude 54∘ 540 W; altitude 206 m) following a randomized complete block design, with three replicates and eight-tree row plots, with a total of 4,601 plants.

In the first year, a gradual increase of defoliation was detected in the trial, caused by a severe infection of Teratosphaeria nubilosa (Cooke) Crous & U.Braun. Therefore, traits associated with growth and response to infection were evaluated. To measure the susceptibility to disease, the degree of defoliation (DEF) was assessed on the whole crown. In this species, the adult foliage is less susceptible to T. nubilosa than juvenile foliage (Milgate et al. 2005; Balmelli et al. 2013). Thus, the precocity of vegetative phase change, which may represent a means of escape from infection, was assessed as the fraction of the canopy exhibiting adult foliage (ADFO). Both disease-related traits were evaluated using a visual scale with classes of 10% at 21 months. The growth traits total height (HT) and diameter at breast height (DBH) were measured at 26 months and at 50 months, respectively. A total of 3,853 individuals presented high-quality phenotypic records in the data set and have been used for the analysis. For a more detailed description of the progeny trial and phenotypic data, see Balmelli et al. (2016).

Genotyping

A subset of 1,008 randomly selected individuals, representing 179 families with 4–8 individuals per family, were genotyped using the Illumina Infinium EUChip60K SNP chip (Silva-Junior et al. 2015) at GeneSeek Inc. (Lincoln, NE, USA). The SNP calling was performed using the Maidenaria section reference. The marker data was filtered to select markers with call rate > 0.90 and a minor allele frequency (MAF) > 0.05, and individuals with call rate > 0.80 using qcf90 software (Masuda et al. 2019). As a result, 16,364 SNPs were selected for analysis from 975 samples. The registration errors in the pedigree were corrected based on SNP information, following the approach of Muñoz et al. (2014). In order to estimate the selfing rate in this population, the 78 parents still standing were also genotyped. The same genotype platform and filtering criteria were used for these individuals. Pairwise linkage disequilibrium (LD) was estimated between SNPs based on the squared correlation coefficient (r2) for SNPs located on the same chromosome. The LD decay was fitted by a nonlinear regression model between adjacent sites using the R script by Marroni et al. (2011).

Selfing rate estimation

The population’s selfing rate was calculated as the proportion of offspring that resulted from self-fertilization based on the estimation of pairwise relatedness between parent-offspring. This analysis was carried out with a subset of 505 individuals, represented by 78 mothers and their offspring (427 individuals), with a mean of 5.5 trees per family (range 3–8). A subset of 1,152 SNP markers with a call rate > 0.90, MAF > 0.05 and in Hardy-Weinberg equilibrium assessed with a chi-squared test (p-value > 0.05) were used to selfing estimation.

Since the performance of algorithms to estimate relatedness varies depending on population composition, the likelihood estimators that allow for inbreeding, Milligan (M) (Milligan 2003) and Wang (W) (Wang 2007), were applied and compared. The use of simulated data is recommended to compare the performance of different estimators, as well as determine the bias and precision (Wang 2011). Thus, simulated marker data were generated to emulate the characteristics of the expected data (relationship types), using the allelic frequency distribution of the empirical markers. The bias and precision were estimated as the root mean square relative error (RMSE) and subsequently applied as an appropriate correction for the relatedness estimators of the real data. The simulated data were generated with the Fam-sim code (https://github.com/timothyfrasier/C_software), and the relatedness coefficients estimated using the related R package (Pew et al. 2015).

The relatedness coefficients estimated for the parent-offspring pairs of the subset of 505 genotyped trees (78 mothers and 427 progeny) were compared with the expected relationship coefficient. Based on the empirical distribution, a threshold was defined by a parent-offspring relationship coefficient larger than one standard deviation from the mean. This threshold was chosen to declare each pair of trees as parent-outbreed or parent-self offspring. This also corresponds to the lack of overlap between distributions for the two new relationships defined (parent-outbreed and parent-self offspring). The corrected pedigree was improved by relabeling the selfed individuals with information from the male parents, and this improved pedigree was used in the subsequent analyzes.

To check the identity of the individuals relabeled as selfed, the inbreeding coefficients were estimated using a genomic relationship matrix (G) for this subset of 505 genotyped trees (VanRaden 2008). The diagonal elements of the matrix G are 1 + F, where F is the inbreeding coefficient. For outcrossed individuals, F will be 0 and the diagonal elements of the matrix G will be 1, while for selfed or consanguineous individuals F will be greater than 0 and the diagonal elements will be greater than 1. Therefore, the average inbreeding in the population will be the average of the diagonal elements of the matrix G minus 1. Three alternative methods of construction of the realized relationship matrix were assessed following VanRaden (2008) and Forni et al. (2011): GOF, where the G matrix is scaled to be analogous for the numerator relationship matrix; GD, weighting markers by reciprocal of their expected variance, and Greg, regressed the genomic relationships on the relationship matrix based on pedigree. These matrices were constructed with the subset of 1,152 SNPs and with the complete set of markers (16,364).

Statistical analysis

Numerator relationship matrix

The average numerator relationship matrix A was computed from the improved pedigree data that included relabeled self-individuals. Additionally, following the methods described by Dutkowski et al. (2001), a modified numerator relationship matrix (As) was estimated to take into account the selfing rate in the population. Both matrices were created in the ASReml-R version 4.0 (Butler et al. 2018; R Core Team 2018) using the ainverse command, with the argument selfing incorporating the selfing rate previously estimated from the genotyped parent-offspring subset of trees in the As matrix.

Pedigree-based model

The following linear mixed model was applied for the pedigree-based model (ABLUP) to estimated breeding values for each trait:

$$y = X\beta + Z_{p} p + Z_{a} a + \varepsilon $$

where y is the vector of phenotypic observations, β is the vector of fixed effects, such as the overall mean and block, p is the vector of random plot effects, a is the vector of random effects of individual trees (i.e., breeding values), and ε is the vector of random residuals. The incidence X matrix relates the observations to the fixed effects, and Zp and Za are the corresponding incidence matrices related to random effects p and a. The vectors of plot and residual effects follow a \(var(\boldsymbol {p}) \sim N (0, \boldsymbol {I} {\sigma ^{2}_{p}})\) and \(var(\boldsymbol {\varepsilon }) \sim N (0, \boldsymbol {I} \sigma ^{2}_{\varepsilon })\) respectively, where I is the identity matrix, \({\sigma ^{2}_{p}}\) the plot variance and \(\sigma ^{2}_{\varepsilon }\) the residual variance. In the pedigree-based approach the vector a was assumed to follow a \(var(\boldsymbol {a}) \sim N (0, \boldsymbol {A} {\sigma ^{2}_{a}})\) where A is the average numerator relationship matrix and \({\sigma ^{2}_{a}}\) is the additive genetic variance. In order to investigate the effect of the selfing rate on the estimation of breeding values, a conventional A matrix has been used (ABLUP_S0), in addition to the As which considers the estimated selfing rate for the population (ABLUP_S05).

Single-step pedigree-genomic-based model

In the single-step genomic blup method (ssGBLUP), both pedigree-based relationship and genomic-based relationship were incorporated into a single relationship matrix (H) (Aguilar et al. 2010). The same linear model as for the pedigree-based method was used, but the A matrix was substituted by the H matrix.

First, the genomic relationship matrix was constructed following VanRaden (2008):

$$G = \frac{ZZ^{\prime}}{2 \sum p_{j}(1-p_{j})}$$

where Z is an n × m matrix of centered genotype scores (n= 975 is the number of genotyped individuals and m= 16,364 is the number of markers), and pj is the reference allele frequency of the jth marker.

A critical step in the single-step evaluation is the adjustment of the genomic-based relationship matrix to be compatible with the pedigree-based relationship, to avoid a lack of convergence, large reranking or biases in the analyses (Misztal et al. 2013). For this reason, the G matrix was scaled so that the average of its diagonal elements and the average of the off-diagonal elements equal their corresponding averages on the pedigree-based relationship matrix only for the genotyped individuals (A22 matrix) (Christensen 2012).

As the matrix G is not positive definite, to avoid potential problems with its inversion, it was weighted as proposed by Aguilar et al. (2010) with the scaled parameter α = 0.95 as

$$G = \alpha G + (1 - \alpha) A_{22}$$

The inverse of the relationship matrix that combines pedigree and genomic information (H− 1) was derived by Aguilar et al. (2010) as

$$H^{-1} = A^{-1} + \begin{bmatrix} 0 & 0 \\ 0 & G^{-1} - A_{22}^{-1} \end{bmatrix} $$

where A− 1 is the inverse of the pedigree-based relationship matrix A, and G− 1 and \(\boldsymbol {A_{22}^{-1}}\) are the inverse of the genomic and pedigree relationship matrices for the genotyped individuals, respectively.

Two alternative pedigree-based matrices were used for the construction of the matrix H: (i) a conventional A− 1 and \(\boldsymbol {A_{22}^{-1}}\) matrix (ssGBLUP_S0) and (ii) an As (As− 1 and \(\boldsymbol {As_{22}^{-1}}\)) matrix modified including the populational selfing rate (ssGBLUP_S05).

The G and H matrices were calculated using the preGSf90 software (Aguilar et al. 2011). The four models: ABLUP_S0, ABLUP_S05, ssGBLUP_S0 and ssGBLUP_S05 were analyzed in BLUPF90 software (Misztal et al. 2002).

Model evaluation

Heritability and model-based accuracy

The narrow sense heritability for all traits was estimated as follows:

$$h^{2} = \frac{{\sigma^{2}_{a}}}{{\sigma^{2}_{a}}+{\sigma^{2}_{p}}+\sigma^{2}_{\varepsilon}} $$

where \({\sigma ^{2}_{a}}\) is the additive genetic variance, \({\sigma ^{2}_{p}}\) is the plot variance, and \(\sigma ^{2}_{\varepsilon }\) is the residual variance.

The model-based accuracy (r) of the predicted breeding values was estimated across the four models as follows:

$$ r = \sqrt{ 1- \frac{PEV}{(1+F_{i}) {\sigma^{2}_{a}}}} $$

where PEV (prediction error variance) for the ith tree is the diagonal element of the inverse of the coefficient matrix of mixed model equations, and the diagonal elements of A or H contain the inbreeding coefficient of the ith individual as 1 + Fi, depending on ABLUP or ssGBLUP (Mrode 2014).

The Akaike Information Criteria (AIC) (Akaike 1974) was used to compare the fit of models and the significance of the selfing rate when this information is included in the model. Additionally, to compare whether the individual tree ranks differed among the models, the Spearman rank correlation was estimated. The proportion of common candidates in the top ranked 10% (385 trees) was compared among the four different models.

Cross-validation models

The predictive performance of each model was evaluated through a 10-fold cross-validation approach. Since the training population is structured as half-sib families with different levels of relationship between them, as open-pollinated families sharing common grandparents, two different strategies were employed to split the data into training and validation sets. For the first method (CV-random), the data set was randomly split in ten non-overlapping subsets, each containing equal number of genotyped and non-genotyped individuals. In the second strategy (CV-family), the ability to accurately predict breeding values based on genomic information of other family or distant relationship pedigree (e.g., grandparent level) was assessed. Thus, the whole family was sampled, so ten subsets approximately of the same size were created, each containing all individuals (genotyped and non-genotyped) of between 18 and 20 families. For both approaches, one subset was used as a validation population while the remaining subsets were used to predict the led-out individuals in the first population. This process is then repeated 10 times with each subset used exactly once as the validation data set. The above analysis was repeated 100 times, including new randomly assigned splits of individuals (CV-random) or families (CV-family).

The predictive ability can be estimated as the correlation between the predicted and the “true” breeding values. Since these values are unknown, the breeding values estimated with the pedigree, phenotypic and genomic information of all available trees were considered as the best estimates of “true” breeding values and used as reference. The Pearson correlation between the predicted breeding values only of genotyped individuals in validation data sets and the reference breeding values were calculated. Predictive ability was estimated as the mean correlation values of all validation data sets.

The prediction bias was calculated as the regression coefficient between the reference breeding values and those predicted with the different models (Isik et al. 2017). A regression coefficient of 1 indicates no bias, whereas values greater than one indicate deflation and values smaller than one indicate inflated predictions. The Spearman rank correlation was also calculated between the reference and predicted breeding values to determine if the ranking differed among approaches.

Results

Selfing estimation

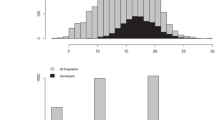
The simulation study showed very consistent performance for M and W likelihood estimators, with positive small bias in both pairwise relatedness for the parent-offspring relationship class (0.011 and 0.010 for M and W estimators, respectively). This result allows us to evaluate the resolution expected and correct the estimated pairwise relatedness of the empirical data. Since highly similar results and a high correlation were found between the M and W likelihood estimators in the E. globulus real data, only results for the W estimator are shown. The distribution of the parent-offspring pairwise relationship is expected to be normal, centered at 0.5. Nevertheless, the 427 pairwise relationships evaluated presented a bimodal normal distribution. The primary peak occurs at the expected value (0.5) and a second, much smaller peak occurs around 0.8 (Fig. 1). From the observed distribution and using a threshold defined by empirical data, 23 pairwise relationships were declared inconsistent; thus, 23 individuals were identified as selfed progeny (5.4% of the sample) and reassigned in the improved pedigree with complete parent information. These self-individuals presented above 0.7 and up to 0.9 pairwise relationships coefficients, well above those expected for a parent-offspring.

Fig. 1
figure 1

Distribution of pairwise relatedness coefficients for parent-offspring using likelihood estimator (expected value = 0.5). The vertical dashed line corresponds to the threshold used to identify selfed individuals in the population

Full size image

Genomic relationship matrices, computed following three alternative methods, confirmed the pairwise relationship classification obtained from the likelihood estimators. The genomic matrices computed using the subset and the complete set of markers were comparable, with correlations between them of 0.92, 0.92, and 0.86, for GOF, GD and Greg matrices, respectively. The estimated average inbreeding was remarkably high for selfed progeny (0.25), whereas the outbred progeny showed an observed value of − 0.02, close to the expected value (0.0) derived from the diagonal of the GOF matrix computed with the subset of 1,152 markers. The same pattern was observed for the GD and Greg matrices, with an average of 0.23 and 0.30 for selfed progeny and − 0.01 and 0.0 for outbred progeny. Although a lower inbreeding was observed with the complete set of markers for the selfed progeny, the differences were consistent between both groups of individuals for the GOF matrix (0.09 and − 0.14 for selfed and outbred progeny). Moreover, this difference was maintained in GD and Greg matrices, where the average inbreeding was 0.13 and 0.21 for selfed individuals, and − 0.10 and − 0.07 for outbred progeny, respectively. When the covariance of the parent-offspring was evaluated, clear differences were observed between the two new parent-offspring relationship declared. The mean parent-offspring covariance for parent-outbred offspring was 0.48, 0.49 and 0.49 for the GOF, GD and Greg matrices, close to the expected value of 0.5. Likewise, mean values of 0.87, 0.85 and 0.91 were derived from the GOF, GD and Greg matrices for the new category of parent-self offspring (expected value 1.0). Similar results were observed for the complete set of markers.

Genetic relationship matrices

Both pedigree data and marker information were used to estimate relationship between individuals in the progeny trial of open-pollinated families. The numerator relationship matrix (A and A22) was very sparse, with discrete class between individuals with coefficients ranging from 0 to 1.5 (unrelated to identity self offspring). As expected, the relationship coefficient between individuals for each discrete class increased with the incorporation of the population selfing rate (As and As22). Conversely, the realized relationship matrix based on genomic information presented a continuous distribution with values between − 0.128 and 1.477 (Table 1). Thus, the use of marker information allowed to estimate the proportion of genome shared by different individuals, capturing the specific level of relatedness between individuals and relationships not registered by pedigree.

Table 1 Mean (and standard deviation) of the estimated pairwise relatedness coefficients for each relationship class for three relationships matrices: A22 average numerator relationship matrix for genotyped individuals; As22 average numerator relationship matrix for genotyped individuals including 5% populational selfing rate and G: genomic-based relationship matrix
Full size table

The mean values within the different relationship groups tended to be higher for pedigree matrices with and without incorporation of populational selfing rate for genotyped progeny (A22 and As22), compared to the G matrix (Table 1). Particularly, higher mean values were obtained when the populational selfing rate was incorporated. Despite this apparent overestimation of relatedness, the incorporation of selfing rate in the numerator relationship matrix resulted in a slight increase in the correlation between this matrix and the G matrix (0.765), compared with the matrix that did not take into account the population’s selfing rate (0.756).

Model comparison

The heritability estimates obtained with the genomic model (ssGBLUP_S0) were lower than with the pedigreed-based model (ABLUP_S0) for disease resistance traits, and equal or moderately higher for growth traits (Table 2). The heritability varied from 0.33 to 0.66 in ABLUP_S0 and from 0.29 to 0.62 in the ssGBLUP_S0 approach. The incorporation of the population selfing rate yielded a marginal reduction in the pedigreed based model (ABLUP_S0 vs ABLUP_S05) and in the genomic model (ssGBLUP_S0 vs ssGBLUP_S05). In addition, the AIC values showed that the genomic information improved the goodness-of-fit compared with the based-pedigree models for all traits (Table 3). For traits associated with the response to infection, the best fit was reached with the model that also consider populational selfing rate (ssGBLUP_S05), whereas for growth traits, the lowest AIC values correspond to genomic model in absence of selfing rate (ssGBLUP_S0).

Table 2 Heritability (and standard deviation) for models ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to selfing rate in the population); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to selfing rate in the population)
Full size table
Table 3 Akaike information criteria (AIC) for models ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to selfing rate in the population); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to selfing rate in the population)
Full size table

Model-based accuracies of the predicted breeding values were evaluated for three classes of individuals: maternal parents, non-genotyped and genotyped offspring (Fig. 2). Accuracies for breeding values of maternal parents were quite similar for the four models evaluated, with averages across traits of 0.663 (ABLUP_S0), 0.678 (ABLUP_S05), 0.698 (ssGBLUP_S0) and 0.708 (ssGBLUP_S05). The inclusion of genomic information slightly increases the theoretical accuracy of the maternal and progeny breeding values, with the exception of disease-related traits in non-genotyped offspring. The incorporation of population selfing rate, both in the pedigree and genomic models (ABLUP_S0 vs ABLUP_S05 and ssGBLUP_S0 vs ssGBLUP_S05), did not generate a significant improvement in progeny accuracy either. For the genomic approaches, the mean of genotyped progeny accuracies for all traits (0.768 and 0.769, for ssGBLUP_S0 and ssGBLUP_S05) were higher than non-genotyped progeny (0.670 and 0.675, for ssGBLUP_S0 and ssGBLUP_S05), as was expected.

Fig. 2
figure 2

Mean theoretical accuracies of breeding values for three classes of individuals: maternal parent (M), non-genotyped offspring (NO) and genotyped offspring (GO) for models fit using pedigree-based (ABLUP_SO), pedigree-based incorporating selfing rate in population (ABLUP_S05), pedigree-genomic-based models (ssGBLUP_S0) and pedigree-genomic-based incorporating selfing rate in population (ssGBLUP_S05)

Full size image

The proportion of common progeny candidates in the top 10% (385 trees) ranking was used as a measure of the impact to include genomic information and selfing rate in the breeding values estimation (Table 4). The proportion of common candidates between ABLUP and ssGBLUP ranged from 76.3 to 89.3% when the populational selfing rate was not included in the models, and from 75.0 to 90.1% when it was included. These values indicate that there will be some changes in the ranking of individuals when genomic information is included, regardless of the incorporation of selfing rate. When the impact of populational selfing was evaluated, the proportion of common candidates varied for the different traits from 95.3 to 98.6% for ABLUP_S0 and ABLUP_S05, and from 97.3 to 99.1% for ssGBLUP_S0 and ssGBLUP_S05. These higher values indicate that selfing rate has low impact in the ranking of selections.

Table 4 Percentage of common trees in the top ranked 10% for different traits between the four models evaluated: ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to selfing rate in the population); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to selfing rate in the population)
Full size table

Cross-validation

The predictive ability of ABLUP_S0 ranged from 0.497 to 0.614 and from 0.098 to 0.272 in the CV-random and CV-family cross-validation methods, respectively (Fig. 3). In comparison, the predictive ability for the ssGBLUP_S0 model ranged from 0.680 to 0.842 in the CV-random and from 0.546 to 0.720 in the CV-family approach. The predictive abilities of the pedigree-genomic-based models (ssGBLUP) were always higher than those of the pedigree-based (ABLUP) models in both CV methods. Thus, the predictive abilities decreased 30% in the CV-random method for all traits when comparing ssGBLUP vs ABLUP models. However, the reduction was especially strong, 60% for resistance traits and 80% for growth traits, when the relatedness between training and validation populations was intentionally removed (CV-family). This was expected, considering that for growth traits predictive abilities around 0.1 were found in the CV-family method. When we assessed the pairwise LD in this population, the LD decayed to an r2 of 0.2 within 21.8 kb (Supplementary Fig. 1). Thus, some LD between markers and QTLs could be driving the predictions. The models that included the selfing rate had predictive abilities very similar to those of the homologous models with conventional A matrix (ABLUP_S0 vs ABLUP_S05 and ssGBLUP_S0 vs ssGBLUP_S05).

Fig. 3
figure 3

Predictive abilities of two cross-validation methods: random (CV-random) or between family relatedness (CV-family) for four phenotypic traits and the four models: ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to populational selfing rate); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to population selfing rate)

Full size image

The degree of bias of the breeding values was low, with the pedigree-genomic-based methods showing lower bias (i.e., regression coefficients closer to one) compared to those of pedigree-based methods. Greater biases were observed for the CV-family cross-validation compared to the randomized cross-validation, with deflated predictions for disease resistance traits and inflated for growth traits (Fig. 4). The inclusion of populational selfing rate in the models had almost no effect on bias. The Spearman rank correlations were close to the predictive ability and followed the same trend. Thus, the models with higher predictive abilities also presented higher rank correlation values. The inclusion of the selfing rate in the models also had no effect in the Spearman rank correlations (Fig. 5).

Fig. 4
figure 4

Bias (regression slope) of two cross-validation methods: random (CV-random) or between family relatedness (CV-family) for the four phenotypic traits and the four models: ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to populational selfing rate); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to population selfing rate)

Full size image
Fig. 5
figure 5

Spearman rank correlation of two cross-validation methods: random (CV-random) or between family relatedness (CV-family) for four phenotypic traits and the four models: ABLUP_S0 (pedigree-based); ABLUP_S05 (pedigree rescaled to populational selfing rate); ssGBLUP_S0 (combined pedigree marker-based) and ssGBLUP_S05 (combined pedigree marker-based rescaled to population selfing rate)

Full size image

Discussion

Populational selfing rate

Molecular tools have been proven to be useful to study the mixed-mating system in Eucalyptus species (Tambarussi et al. 2018). Currently, the estimation of the outcrossing rate is mainly based on kinship allocation or sibling reconstruction methodologies (Kalinowski et al. 2007; Wang et al. 2012). Because these strategies were developed to work with a limited number of multiallelic markers, they are methodologically complex and computationally demanding, so it is difficult to use them efficiently in large SNP data sets. However, as we demonstrated in this study, comparing the expected and empirical distributions of relationship estimators for parent-offspring provides a straightforward procedure to identify progeny derived from selfing events. Although this strategy can only be implemented when a set of parental individuals are genotyped, the clear bimodal distribution for the parent-offspring relationships enabled to unequivocally identify individuals derived from self-fertilization (Fig. 1).

The precision of the pairwise relatedness estimates, as well as correct assignment of individuals to their relatedness category, mainly depends on the number and informativeness of molecular markers and the sample size. Simulations under different mating systems scenarios showed that a number of 800 SNPs are enough to obtain a rate of 95% of correct assignment (Kopps et al. 2015). Cappa et al. (2016) showed that 181 SNP markers allowed the estimation of the actual relatedness among 166 individuals from an open-pollinated progeny of E. grandis. Similarly, Klápště et al. (2017) employed a subset of 500 SNP markers for sibship reconstruction of 691 trees from an open-pollinated family of E. nitens. In our study, the number of neutral markers (1,152 SNPs) and the population size (427 parent-offspring pairwise comparisons) are higher than those used in other studies in forest tree species.

For open-pollinated progenies of Eucalyptus species, it is traditionally considered that up to 20–30% of individuals are selfed (Griffin and Cotterill 1988; Volker et al. 1990). These reference values were based on outcrossing rates reported for 10 Eucalyptus species evaluated with isoenzymes loci in seeds or seedlings derived from natural populations (Moran and Bell 1983). In our study, a remarkably low value was obtained (5.4%) for a 7-year-old breeding population of E. globulus growing in exotic conditions. The discrepancy with the reference values can be explained for both environmental and genetic factors. First, in seed orchards and breeding populations the selfing rate may be lower than in natural populations, because all trees are of the same species and age, which favors the synchronization of flowering. Secondly the values of selfing reported by Moran and Bell (1983) were based on studies carried out on seeds or seedlings, while the reports of selfing rates of breeding populations are obtained from trees growing in progeny tests, where many selfings may have dead at early ages due to inbreeding depression. Finally, differences in statistical methods and molecular marker technology may explain the low estimated selfing rate. Recent studies, using multiallelic molecular markers, reported selfing rates between 7.4 and 8.3% for E. urophylla (Grattapaglia et al. 2004; Pupin et al. 2019) and between 1.8 and 3.2% for E. camaldulensis (Gonzaga et al. 2016). Klápště et al. (2017), using SNP genomic data for pedigree reconstruction and selfing estimation, reported a selfing rate of 4.0% in E. nitens.

As the selfing rate is specific to a mating event, and can vary among species, populations, and trees and fruits within trees, it is necessary to estimate it from marker data taken from the population under study. However, for tree species is infrequent to genotype a complete population, so it is not possible to identify all self-fertilized individuals. In this study, the populational selfing rate, estimated with a small fraction of the total number of trees, was used as a correction factor for the relationship matrix based on pedigree for the complete population. This correction, with the estimated population selfing rate of 5.4%, resulted in a more reliable relationship information, allowing a more accurate estimation of genetic parameters and breeding values.

Heritability with selfing and genomic information

It is well known that analyzing open-pollinated progenies as half-sib families without considering selfing results in over-inflated additive genetic variances and heritabilities (El-Kassaby et al. 2012). The heritabilities estimated in this study decreased between 1.5 and 8.0% when the selfing rate in the population was incorporated into the pedigree-based model (Table 2). The same pattern was observed by Klápšte~ et al. (2018) when comparing different selfing probabilities. On the other hand, the heritabilities estimated with the marker-based approach were lower than the obtained from pedigree-based models for the diseased related traits and equal or slightly higher for growth traits. The marker-based approach is considered more effective for capturing the full genetic relationships among individuals, including selfing events, resulting in more accurate estimates of the genetic variances (Mphahlele et al. 2020; Müller et al. 2017). This is supported by the improvement of fit (measured through the AIC) obtained with the genomic models.

The discrepancies between rankings obtained with traditional ABLUP and ssGBLUP suggest that including genomic information has an impact on the selection of superior individuals. Other studies in forest trees have demonstrated the increase in the breeding values accuracies by including genomic information, thus increasing the probability of a correct ranking of candidates for selection (Cappa et al. 2019; Ratcliffe et al. 2017). In particular, the single-step evaluation, where the genomic relationship between genotyped individuals is projected on non-genotyped individuals, resulted in a more accurate modeling of individual relationships. However, the inclusion of a modified pedigree relationship matrix, accounting for the population selfing rate, did not result in a significant improvement of the breeding values, which is evidenced by minimal changes in the ranking of individuals. Therefore, our results suggest that the inclusion of a genomic relationship matrix in a complete genomic evaluation can efficiently capture the cryptic genetic relationships (including selfing), at least in populations with a low selfing rate.

Performance of the prediction models

As a benchmark for accuracy assessments of genomic selection, predictive abilities are measured as the correlation between the estimated breeding values and the true breeding values. As the true breeding values are typically unknown, the breeding values estimated using the pedigree information (Cappa et al. 2019), or phenotypic values adjusted by experimental effects, are commonly used as reference values (Resende et al. 2012; Zapata-Valenzuela et al. 2013; Isik et al. 2016). However, we assume that a better estimate of the true breeding values can be achieved by considering all sources of information available, so the breeding values estimated through the simultaneous use of phenotypic, pedigree and genomic information were considered as the standard for comparison. For all traits and cross-validation schemes, the approach that included genomic information outperformed the pedigree-based model, without significant differences with the inclusion of the population selfing rate (Fig. 3). These results are consistent with previous reports on forest tree species that included genomic information using ssGBLUP, GBLUP or Bayesian methods (Ratcliffe et al. 2017; Tan et al. 2017). The higher predictive abilities obtaining with the pedigree-genomic-based models may be due to a more precise estimation of genetic relationships captured by markers, i.e., Mendelian segregation. This is specially relevant in breeding populations based on open-pollination, with incomplete pedigree and unknown relationships, where the half-sibs families also include some full-sibs as well as inbreed progeny derived from selfing or mating between close relatives.

The relatively high predictive abilities obtained for traits associated with response to infection by T. nubilosa suggest a genetic control under an infinitesimal model, encouraging the application of genomic prediction schemes for these traits in forest tree breeding programs. Lower predictive abilities were obtained for growth traits, but the values are consistent with previous reports in Eucalyptus species. For instance, Ballesta et al. (2018) reported mean predictive abilities of 0.50 and 0.43 for height and DBH in E. globulus; Resende et al. (2012) reported values between 0.46 and 0.55 for the same traits in hybrid populations, and Müller et al. (2017) reported predictive abilities from 0.34 to 0.44 for E. pellita. However, accuracy comparisons between different studies should consider differences in trait heritabilities, markers set, training and validation population sizes and cross-validation methods.

Relatedness between training and validation data sets is another aspect that has a large impact on predictive abilities (Habier et al. 2007). As expected, the predictive abilities for all traits were higher for the CV-random schemes, compared with the CV-family approach where close pedigree relationships between the training and validation data set were intentionally avoided. However, applying the latter approach, low to moderate predictive abilities were obtained with pedigree-based models, suggesting that some historical relatedness persist between families of the training and validation populations. Also, in this open-pollinated population, the paternal connections between families are not accounted in the pedigree. When marker information was incorporated, the predictive abilities obtained with the CV-family approach were moderately high, and slightly lower than those obtained with the CV-random approach. Thus, in addition to capturing distant relatedness between families, the predictive abilities obtained with genomic information could also be explained by the presence of stable linkage disequilibrium between markers and QTLs across different families. Our results, in line with previous studies in open-pollinated populations of forest tree species, show that markers reveal information about genetic relationships among individuals, as well as historical linkage disequilibrium (Beaulieu et al. 2014). Results are encouraging for breeders relying on open-pollinated material, who may question the use of genomic selection in populations with low apparent relationship.

Conclusions

This research demonstrated that the estimation of pairwise relationships and their comparison with the expected value for parent-offspring relationship is a simple and fast tool to estimate the selfing rate in a forest population. The estimation of the actual selfing rate in the population allows for more reliable estimation of genetic parameters, avoiding the upward bias in additive genetic variance estimates resulting from the use of reference values. Also, the selfing rate can be easily incorporated in a numerator relationship matrix, and this modified matrix can be combined with a genomic relationship matrix to incorporate all the advantages of the genomic selection approach in one procedure. The inclusion of the phenotype of genotyped and non-genotyped trees in a single analysis proved to be effective for the accurate estimation of genetic parameters and to improve the prediction of breeding values. However, the effect of incorporating the population selfing rate in the numerator relationship matrix in a single-step genomic analysis needs to be investigated under higher selfing rates.