Abstract
Tree health and growth rate must both be considered in Scots pine breeding for harsh areas such as northern Sweden. Univariate (UV) and multivariate (MV) multi-environment trial (MET) analyses of tree vitality (a measure of tree health) and height (a measure of growth rate) were conducted for four series of open-pollinated Scots pine progeny trials (20 trials total), to evaluate age trends, patterns, and drivers of genotype-by-environment interaction (G × E). The lowest standard errors were obtained for the MV MET analyses, indicating that MV analyses are preferable to UV analyses. By incorporating factor-analytic structures, the most complex data sets could be handled, suggesting that factor-analytic analyses are preferred for evaluation of forest progeny trials. We detected strong patterns of G × E for both tree vitality and height, and the driver of G × E was found mainly to be differences in degree day temperature sum, such that G × E was higher between trials with more contrasting temperature sums. The genetic correlations, between vitality and height within sites, were generally positive and were driven by the harshness of the trial; mild trials had lower genetic correlations than did harsh trials. The sign of the across-site genetic correlations between vitality and height changed from positive to negative in some cases, as the differences between the temperature sum of the trials increased. These findings support the hypothesis that tree height assessed in harsh environments with low survival is likely to reflect health and survival ability to a greater extent than growth capacity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In harsh climates, such as in northern Sweden, both individual tree vitality (a measure of survival ability, over the range from healthy to dead) and growth impact forest productivity (Ruotsalainen and Persson 2013). They are therefore important traits in tree breeding programs to maximize stand volume production.
In cold northern areas, mortality in artificially regenerated Scots pine (Pinus sylvestris L.) forests is seldom caused by a single event but is usually the result of damage accumulated over several years (Eiche 1966; Stefansson and Sinko 1967). The accumulated injuries are primarily related to the harsh climate, reducing the plant’s capacity to grow and develop during subsequent growing seasons. This may result in further damage (climatic-, fungal-, or insect-related), increased mortality and suppressed the growth of surviving-but-damaged individuals. In Scots pine regeneration in cold areas, two of the most common fungi for which additive genetic variation in resistance has been reported are Gremmeniella abietina (Lagerb.) and Phacidium infestans L. (Persson et al. 2010). As a consequence of accumulated damage, only unstressed and healthy individuals are likely to express their growth potential fully, which in turn may influence the genetic association between tree vitality and growth. The major proportion of mortality occurs during the first years after planting and typically decreases considerably after the trees reach 20 years of age (Persson and Ståhl 1993). The reduced mortality related to tree size and aging may be explained by the remaining individuals being more hardy and less sensitive to near-ground environmental disturbances as the trees mature.
Multivariate (MV) within-site analyses of northern Scots pine trials found generally positive additive genetic correlations between tree vitality and height in the age range 6 to 27 years (Olsson and Ericsson 2002; Persson and Andersson 2003). In a MV analysis of three series of Scots pine trials, Kroon (2011) found generally that within-site correlations between vitality and height were positive at young ages on harsh sites, but that correlations weakened as the trials aged. Kroon (2011) also showed that the pattern of within- and across-site genetic correlations between health and growth traits changed from positive to negative when the two traits were expressed in contrasting environments.
Perttu and Morén (1994) showed a strong relationship between tree growth and temperature sum (Tsum) in degree days, at the planting site, with a threshold value of + 5 °C. Tsum is used and recommended as a climate index for operational forestry applications in Sweden and Finland (Bärring et al. 2017). It is of great interest to examine whether there is a general trend, whereby the genetic correlations between growth and vitality are associated with the degree day Tsum at the sites.
In crop and tree breeding, multi-environmental trials (MET) are established to evaluate the degree and pattern of genotype-by-environment interactions (G × E interactions, or G × E), as well as to test the robustness in performance of genotypes in different environments. In this context, type B genetic correlations (Burdon 1977), i.e., correlations between the same trait in different environments, can reveal rank changes among genotypes across different environments and are therefore widely used to evaluate the degree of G × E (Baltunis et al. 2010; Kelly et al. 2007; Li et al. 2017; Smith et al. 2015; Ukrainetz et al. 2018; Zapata-Valenzuela 2012).
Nevertheless, more complex patterns of G × E can be distinguished when multiple traits are analyzed, such as type A genetic and phenotypic correlations (i.e., correlations between different traits within the same environment) differing among environments, and type AB genetic correlations (term proposed by Li et al. 2017), i.e., correlations between different traits expressed among environments. Also, according to Mathew et al. (2016), MV analysis is generally more accurate and powerful than across-site univariate (UV) analysis, because it is able to harness the possible hidden correlation structure that can exist among different variables. In a study with simulated data, Bauer and Leon (2008) concluded that a larger selection response was obtained with MV analysis than with UV analysis, and they also observed lower overall standard error (SE) in MV analysis. Moreover, if the trees in a trial are exposed to non-random mortality, the probability of obtaining biased genetic correlation estimates is greater with UV analysis compared with MV analysis, since UV analysis cannot take into account the factors to which the selection process is related, in our case, tree vitality (Persson and Andersson 2004, and references therein).
Factor analytic (FA) variance-covariance structures in mixed models have been used in MET analysis of crops (Beeck et al. 2010; Kelly et al. 2009; Kelly et al. 2007; Smith et al. 2001; Smith et al. 2015) to account for the heterogeneity of variances and correlations that traditional methods, such ANOVA under the assumption of compound symmetry, cannot provide when many traits and sites are involved (Meyer 2009). FA structures mainly summarize the pattern of G × E, by generating several latent variables that account for G × E (Smith et al. 2001). Furthermore, FA structures are considered a good approximation to unstructured (US) variance-covariance structures, but require fewer parameters (Isik et al. 2017; Kelly et al. 2009; Kelly et al. 2007; Smith et al. 2015). FA models are named with the number of multiplicative terms (k factors) so that a model with k factors can be denoted as a FAk model. More recently, several MET studies in forest tree species have used FAk, e.g., in Eucalyptus hybrids (Hardner et al. 2010), Pinus radiata D. Don (Cullis et al. 2014; Ivkovic et al. 2015; Smith and Cullis 2018), Pinus taeda L. (Gezan et al. 2017; Ogut et al. 2014), Picea abies (L.) Karst. (Chen et al. 2017), or Pinus contorta Douglas ex Louden (Ukrainetz et al. 2018), showing an improvement in prediction accuracy in most cases.
The objectives of this study were the following: (1) compare the utility of UV and MV MET analyses; (2) estimate genetic correlations between tree vitality and tree height, at different ages, in different environmental conditions, based on the robust method; (3) test whether there is a dynamic relationship between site harshness and genetic correlations, and whether G × E is related to temperature heterogeneity among sites; and (4) estimate additive and environmental coefficients of variation for vitality and height at two ages, in four unrelated series of five open-pollinated (OP) Scots pine progeny trials (20 trials in total), in northern Sweden.
Materials and methods
Genetic material, experimental designs, and assessed traits
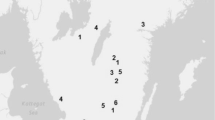
The study used data for tree vitality and height from four unrelated series of progeny trials, each comprising an independent set of OP families collected from Scots pine plus trees. The trials are part of the northern Swedish tree improvement program at Skogforsk. Each trial series comprised of five field trials with between 288 and 360 families. The selected plus trees were assumed to be unrelated, as they were widely separated in 30- to 50-year-old naturally regenerated forest stands, or in stands regenerated by direct seeding or planting of seedlings from locally collected bulked seed (occasionally from the seed of unknown origin). The stands accepted for plus tree selection were typically 5–10 ha, fully stocked, with healthy, well-growing trees. Between two and 30 trees were selected from each of 33–40 stands in each series.
The field trials were planted with 1-year-old container seedlings in a randomized single-tree plot design. The seedlings were grown from OP seeds collected on the plus trees in the original forest stands. Most of the OP families within a trial series were represented in all five field trials. In the majority of the trials, both tree vitality and height were measured on two occasions. The age of the trees at the time of the first measurement varied from 9 to 13 years and from 18 to 22 years for the second (Tables 1 and 2), with the range of age ratios between assessments (Lambeth 1980) varying between 0.47 to 0.63. Reflecting survival ability, tree vitality was scored on all originally planted tree positions at the first and second assessments (V1 and V2) for each individual in four ordered classes: healthy, slightly damaged, severely damaged but still alive, and dead (or missing). Heights at the first and second measurements (H1 and H2) were measured in all living trees from ground to terminal bud. Tsum for each trial (Table 1) was based on estimates from Bärring et al. (2017).
Statistical analyses
Initial analyses
Normal score transformation was performed on the vitality scores to linearize the data with mean zero and standard deviation one, using the proportion of outcomes in the different classes (Gianola and Norton 1981). Back transformation to the real scale was then possible using an arbitrary mean of 50%. Large-scale environmental variation in the trials was taken into account by using a post-blocking procedure (Ericsson 1997). In addition, and prior to any other analyses, UV single-trial spatial analyses were performed, using ASReml (Gilmour et al. 2015), with the objective to adjust the data for within-trial micro-environmental effects (see Supplementary Material S1). Diagnostic tools, variograms, and plots of spatial residuals were used to detect design, treatment, local, and extraneous effects. The predicted design effects and spatial residuals were extracted from the ASReml output files and used to remove estimated environmental effects from the raw data (Chen et al. 2017; de la Mata and Zas 2010). The environmentally adjusted individual tree data were then used to perform the genetic analyses described in the following sections.
Model structures
With the aim to detect differences in estimated genetic variances and parameters, and in the absence of pedigree information (other than seed-parent identity), we performed both UV and MV MET analyses, with family models. Due to the lack of family connections among trial series (Fig. S1), all the analyses were performed within series (Tables 1 and 2). For each analysis, and with the objective to detect the most accurate method, we fitted up to seven different variance-covariance functions (Tables 3, and S1). All models were fitted using ASReml (Gilmour et al. 2015). To perform MV MET analysis, each variable (V1, V2, H1, and H2) at each trial was considered as a separate trait; therefore, when referring to the MV MET analysis, “trait” denotes a given trait-assessment-trial combination.
The first model fitted an unstructured variance-covariance matrix, parameterized as heterogeneous (co)variances (US model). The second model was similar but parameterized as heterogeneous correlations (CORGH model) between trials and traits. US and CORGH models require n(n + 1)/2 parameters to be estimated, i.e., the genetic variance for each trial or trait and covariance (US) or correlation (CORGH) between each pair of trials or pair of traits.
The remaining models fitted five different factor-analytic (FAk) covariance structures following Smith et al. (2001) and Smith and Cullis (2018). In FAk models, the family effect in trial t (for UV MET analysis) or trait-trial t (for MV MET analysis) is modeled as the sum of k multiplicative terms
Each k term represents the product of the family effect (frj), known as “scores,” and a trial (UV MET) or trait/assessment/trial (MV MET) effect (λrt), known as “loading.” δtj is the error or lack-of-fit in the model. The model can also be written in vector notation as
where u is the m-vector of stacked family effect in each trial or trait-trial (trial or trait-trial by family interaction for UV and MV MET, respectively) vector; λr is the t-vector of trial or trait-trial loadings for the rth common factor and fa is the associated m-vector of family scores; Λ = [λ1, λ2 … λk] is the t × k matrix of factor loadings; ⨂ is the Kronecker product; Im is the m-identity matrix with dimension of m families; \( \mathbf{f}=\left({\mathbf{f}}_{\mathbf{1}}^{\mathbf{T}},{\mathbf{f}}_{\mathbf{2}}^{\mathbf{T}}\dots {\mathbf{f}}_{\mathbf{k}}^{\mathbf{T}}\right) \) is the mk-vector of family scores and δ is the tm-vector of deviations of the effect of the mth family in the tth trial or trait-trial from that predicted by the factors. Family scores and trial or trait-trial deviations were assumed to be normally distributed with zero means and variances, var(f) = Imk, and var(δ) = Ψ ⨂ Im, where Ψ is the t × t diagonal matrix containing trial- or trait-trial variances. Therefore, the variance-covariance matrix for family effects within each trial or trait-trial can be expressed as
Model comparisons were made using model log likelihood, Akaike (AIC), and Bayesian (BIC) information criteria, all appropriate to compare US and CORGH models with FAk. Extended factor analysis (XFAk) is a FAk model with different fitting algorithm and was developed to reduce the computational requirements of FAk models and thus make them easier to converge (Isik et al. 2017). Henceforth, and in order to distinguish between the different variance-covariance structures, we have adopted the acronyms used by ASReml for extended factor analysis and unstructured variance-covariance with heterogeneous correlations methods, i.e., XFAk and CORGH, respectively.
Multivariate and univariate multi-environment trial analyses
The MV MET data set combined between 16 and 19 traits, whereas the UV MET data set comprises single traits combined across trials. The linear mixed model was
where y is the vector of observations (trait-assessment-trial and traits combined across trials, for MV MET and UV MET analyses, respectively); b is the vector of fixed effects (which are intercept and latitudes of the plus tree origins for MV MET analyses, and additionally trial for UV MET analysis) with the associated design matrix X; u is the vector of random family or family-within-trial effects for MV and UV MET analyses, respectively and was modeled by fitting the structures defined in the previous section, i.e., CORGH, US, FAk, and XFAk; Z is the design matrix associated to u; and e is the vector of random residuals; in the case of MV MET analyses, residual variances and covariances were modeled using a US structure model, while for traits measured in different trials, covariances were set to zero. For UV MET analysis, e is the vector of residuals from all trials.
Genetic parameters
Within-trial narrow-sense heritabilities (\( {h}_w^2 \)) were estimated for each trait and trial, assuming that the OP families had true half-sib structure, as\( \frac{4{\widehat{\sigma}}_f^2}{{\widehat{\sigma}}_f^2+{\widehat{\sigma}}_e^2} \), where \( {\widehat{\sigma}}_f^2 \) and \( {\widehat{\sigma}}_e^2 \) are the estimated among family and residual variances, respectively.
Overall, across-trial narrow-sense heritabilities (\( {h}_b^2\Big) \) were estimated within series for each trait according to Isik et al. (2017) as \( \frac{4\ \overline{{\widehat{\sigma}}_{js s\acute{\mkern6mu}}}}{{\widehat{\sigma}}_{js}^2+\overline{{\widehat{\sigma}}_{\varepsilon s}^2}} \), where \( {\widehat{\sigma}}_{js}^2 \) and \( \overline{{\widehat{\sigma}}_{\varepsilon s}^2} \) are the pooled estimates of within-trial family and residual variances, respectively, within the sth trial, and \( \overline{{\widehat{\sigma}}_{jss\acute{\mkern6mu}}} \) is the estimated average covariance between trials.
To evaluate genetic and environmental variation, additive genetic (CVA) and environmental (CVE) coefficients of variation were estimated as \( 100\left(\raisebox{1ex}{$\widehat{\sigma}$}\!\left/ \!\raisebox{-1ex}{$\overline{x}$}\right.\right) \) for height, and \( 100\left[\raisebox{1ex}{$\left[100\Phi \left(\widehat{\sigma}\right)-50\right]$}\!\left/ \!\raisebox{-1ex}{$50$}\right.\right] \) for vitality at assumed 50% average mortality, where \( \widehat{\sigma} \)applies to \( {\widehat{\sigma}}_A \) and \( {\widehat{\sigma}}_E \), which are the additive genetic and environmental standard deviations for \( {\widehat{CV}}_A \) and \( {\widehat{CV}}_E \), respectively; \( \overline{x} \) is the least-square mean for height; and Φ is the standard normal probability distribution function (Persson and Andersson 2003; Persson et al. 2010).
Type A, type B, and type AB additive genetic correlations (rA, rB, and rAB, respectively), and their standard errors were extracted from ASReml output files (Gilmour et al. 2015) and respectively calculated as:
\( {r}_A=\frac{{\widehat{\sigma}}_{\left(t1,t2\right)}}{\sqrt{{\widehat{\sigma}}_{t1}^2{\widehat{\sigma}}_{t2}^2}} \), \( {r}_B=\frac{{\widehat{\sigma}}_{\left(s1,s2\right)}}{\sqrt{{\widehat{\sigma}}_{s1}^2{\widehat{\sigma}}_{s2}^2}} \) and, \( {r}_{AB}=\frac{{\widehat{\sigma}}_{t1s1,t2s2}}{\sqrt{{\widehat{\sigma}}_{t1s1}^2{\widehat{\sigma}}_{t2s2}^2}} \), where \( {\widehat{\sigma}}_{\left(t1,t2\right)} \) is the estimated family covariance between traits t1 and t2; \( {\widehat{\sigma}}_{t1}^2 \) and \( {\widehat{\sigma}}_{t2}^2 \)are the family variances of traits t1 and t2, respectively; \( {\widehat{\sigma}}_{\left(s1,s2\right)} \) is the covariance of family effects of the trait t between trials s1 and s2; \( {\widehat{\sigma}}_{s1}^2 \) and \( {\widehat{\sigma}}_{s2}^2 \)are the family variances of trait t at trial s1 and trial s2, respectively; \( {\widehat{\sigma}}_{t1s1,\kern0.5em t2s2} \) is the family covariance between trait t1 at trial s1 and trait t2 at trial s2; \( {\widehat{\sigma}}_{t1s1}^2 \) is the family variance of trait t1 at trial s1; and \( {\widehat{\sigma}}_{t2s2}^2 \) is the family variance of trait t2 at trial s2. Standard errors of estimated variances and variance ratios were calculated using first-order Taylor series approximation.
Cluster analysis and heatmaps
Heatmaps were implemented through the heatmap.2 function available in the gplots package (Warnes et al. 2016) in the R statistical environment (R Development Core Team 2014), with the objective to illustrate the genetic correlations estimated previously. In addition, also for illustrative purposes, cluster analyses were performed using the hierarchical clustering algorithm through the hclust function from the R package and computing the dissimilarity between genetic correlations among trials, as 1 − r, where r is the genetic correlation.
Results
Descriptive statistics
The wide latitudinal and altitudinal distribution of the field trials implied that there would be a large variation in site index and temperature regime, affecting both field survival and height growth (Tables 1 and 2). The percentage of trees surviving at the first assessment varied between 23.2–94.7 and for the second assessment varied between 12.1–91.9 (Table 1). The average height assessments varied between 102 and 321 cm for H1 and between 326 and 717 cm for H2 (Table 2). The average H1 of trees that were alive at the second assessment varied from 114 to 322, whereas those that were dead varied between 96 and 279 cm.
Model fitting
All results are based on the analysis of environmentally adjusted data. Initially, an attempt to perform a single-step approach (spatial- and UV MET analyses combined) was made, but resulted in a high computational expense (up to 8 h and non-convergence for some models), so that a two-step approach was adopted (Chen et al. 2017; de la Mata and Zas 2010).
Generally, for MV MET analyses, we were unable to fit CORGH, US, and FA2 structures (Table 3), whereas XFAk were more easily implemented, such that a full MV MET analysis was possible with up to 16–19 trait/assessment/trial variables (depending on the series). With five trials per trial series (Fig. S1), we fitted equal variances and genetic correlations with REMLRT, AIC, and BIC (Table S1), for all model structures in the UV MET analysis (i.e., CORGH, US, FA1, XFA1, XFA2, and XFA3 models). XFA3 always showed the lowest SE for both UV and MV MET analyses, but SEs were generally larger for UV MET analysis than for MV MET analysis and were therefore considered less reliable (Table S2), so that all results are based only on the MV MET analyses using the XFA3 model. Variance estimates fixed at a boundary during the single-site spatial analysis were excluded from both UV and MV analysis (i.e., V2-F498, V1, and V2 for F499, V1, and V2 for F509). In addition to those, we excluded as well H1 assessed in trial F560, because at the time of the assessment large amounts of damage from moose were detected in the trial, which could bias the estimates.
Heritabilities and coefficients of variation
In general, from the MV MET analyses, \( {\widehat{h}}_w^2 \) slightly increased with age height (Fig. 1 and Table S3) and did not change for vitality; likewise, the \( {\widehat{h}}_b^2 \) did not vary with age for any trait. The range of \( {\widehat{h}}_w^2 \) varied between 0.08 and 0.29 for H1, between 0.05 and 0.33 for H2, and between 0.01 and 0.18 for both V1 and V2.
In general, the \( {\widehat{CV}}_A \) increased with age for height and slightly decreased with age for vitality in trials with lower Tsum, but increased on the milder trials (Table 4). \( {\widehat{CV}}_E \) for tree height generally decreased with age in trials with higher Tsum (milder ones) and increased with age in harsher trials, whereas for tree vitality, it decreased with age in almost all trials.
The lower \( {\widehat{h}}_b^2 \), if compared with \( {\widehat{h}}_w^2 \), and the large variation of \( {\widehat{CV}}_A \), for both tree vitality and height, confirmed the presence of G × E.
Type A and type AB genetic correlations
The rA and rAB from the MV MET analyses are shown in Table 5 and Fig. 2. In general, rA between vitality and height became positive and stronger as the harshness of the trial (lower Tsum) and mortality increased, whereas the opposite pattern was observed in milder environments with higher Tsum. This pattern is also evident by the strong negative Pearson product-moment correlation between Tsum and rA (− 0.61, p < 0.001), illustrated in Fig. 3.
In trial series 2 and 3, negative rAB were detected between vitality scored on trials with a low Tsum and height assessed on trials with larger Tsum. Between trials with similar Tsum, rAB, were in general, positive and moderate to strong, when both traits were scored in low-Tsum trials. Trial series 1 and 4 did not show the same patterns. However, it should be noted that both trial series 1 and 4 represented more homogeneous Tsum among most of the trials within respective series.
Cluster analysis (Fig. 2 and Fig. S2) showed two clusters in series 2; cluster I formed by all V1 and V2, plus H1 and H2 from the trials with the lowest Tsum within series, whereas cluster II was formed by the remaining H1 and H2. A similar pattern was found in series 3, where H1 and H2 from the trials with the lowest Tsum were grouped in cluster I together with almost all V1 and V2, while in cluster II, V1 and V2 from the trial with the largest Tsum was grouped together with the remaining H1 and H2.
Type B genetic correlations
Within series 2 and 3, we generally observed weak rB from the MV MET analyses (i.e., remarkable G × E) between the trials with the lowest Tsum and those with the largest Tsum within each series, for H1 and H2, as well as for V1 and V2, although the latter showed large SE (Table 6 and Fig. 2). The same trend was observed in the moderate negative Pearson product-moment correlation (− 0.41, p < 0.001) between Tsum differences among trials and rB for H1 and H2, illustrated in Fig. 4, which show that rB weakens as the difference in the Tsum increases. In addition, rB for both tree vitality and height increased slightly with age. Again, trial series 1 and 4 showed a different pattern, such that rB were generally moderate to strong for both traits, with no G × E detected.
Age-age correlations
Age-age genetic correlations from the MV MET analyses (Table 7) between H1 and H2 and between V1 and V2 within the same trial were generally strong and positive, varying from 0.75 to 1.00.
Discussion
Tolerance to harsh climatic conditions in Scots pine regeneration seems to depend, partly, on tree size, and mortality occurs predominately before the trees reach a height of two meters, corresponding approximately to 12–16 years after planting (Persson and Ståhl 1993). The stabilized mortality rate associated with height and age may be explained by increased tolerance among surviving individuals and ability to overcome a near-ground disruptive environment, which in turn may influence genetic parameters for both tree survival and height as the trees grow older.
Both Jansson et al. (2003) and Kroon et al. (2011) in a review of breeding value reports from the Swedish tree breeding program stated that the narrow-sense heritability for height usually increased with age, which is consistent with our study. Olsson and Ericsson (2002) observed that heritability for tree vitality increased with age in a single-site MV analysis of a northern located trial, in contrast to our study, where tree vitality heritabilities commonly did not change with age. We note, however, that while we were able to analyze up to 19 traits simultaneously, Olsson and Ericsson (2002) were limited to a maximum of five variables when vitality was included in the models.
The \( {\widehat{CV}}_A \) for height in Scots pine was reported to decrease with age in two different studies in southern Sweden and southern Finland (Haapanen 2001; Jansson et al. 2003). However, our results showed that the \( {\widehat{CV}}_A \) for height mainly increased with age. The reason could be that in harsh areas of northern Sweden, like in our study, height growth in younger trials is still following an exponential curve, while in older trials and more productive areas of southern Sweden and Finland, height growth has shifted already from an exponential model to be more linear. In addition, we observed that the \( {\widehat{CV}}_E \) for height generally increased with age at harsher trials (but decreased at milder ones), suggesting that trees in harsher trials are still susceptible to environmental disturbances at older ages, which in turn also may influence the additive expression. While both the \( {\widehat{CV}}_A \) and the \( {\widehat{CV}}_E \) increased between the two assessments at the harsher trials, the increase in the narrow-sense heritabilities is to a greater degree due to a larger change in the additive variance than at the milder trials.
In general, a decreasing trend with age of \( {\widehat{CV}}_A \) and \( {\widehat{CV}}_E \) for vitality was reported previously by Persson et al. (2010); accordingly, we observed the same trend in harsh sites, whereas, \( {\widehat{CV}}_A \) for tree vitality in mild sites increased in contrast to harsh sites. The decrease of \( {\widehat{CV}}_A \) on the harsh sites in our study is probably due to the low survival rates in these trials and is caused by the well-known behavior that the variance of a variable declines as the variable mean approaches the lower or upper measurement bounds. The magnitude of the \( {\widehat{CV}}_A \) also agrees with the literature for Scots pine, where that reported for height varies between 5 and 25% (Haapanen 2001), 8–9% (Kroon et al. 2011), 3.1–16.3% (Persson and Andersson 2003), 5.52% (Fries 2012), or 4.36% (Hong et al. 2014). Similar values have been reported for other species, such as 5–8.8% in Pinus radiata (Baltunis and Brawner 2010) or 3.3% in Pinus elliottii Engelm (Pagliarini et al. 2016).
Detection of G × E is important to avoid overestimation of genetic variances, and thereby heritabilities (Li et al. 2017). In our study, G × E was observed by weak type B genetic correlations and the reduction of the overall across trials narrow-sense heritabilities in almost all trial series. We observed generally that rB increased slightly with age for both traits. The increase with age of type B genetic correlations for growth traits has been reported in other pines, such as Pinus elliottii (Dieters et al. 1995) and Pinus taeda (Xiang et al. 2003). Despite the increase of type B genetic correlations with age, we were still able to detect G × E at older ages.
Loehle and Namkoong (1987) addressed the proposition that there is a trade-off between growth potential and climatic/biotic tolerance, where, e.g., energy invested in resistance may reduce growth capacity, or where high growth rate may work as defenses by rapid sealing of wounded parts or help the tree to escape an unfavorable ground-level microclimate. A possible example of that tree size may influence the vitality of Scots pine regeneration in northern areas is the occurrence of the pathogen Phacidium infestans, whose mycelium can only develop and spread under winter snow cover (the average snow depth in northern Sweden rarely reaches above 1–1.5 m), and may cause heavy defoliation. Persson et al. (2010) reported genetic variation in susceptibility to Phacidium infestans in trials from three of the four series presented here. When comparing results in the two studies, a pattern can be seen, where trials with significant genetic variation in susceptibility to Phacidium infestans coincide in all cases with those having significant positive type A correlation between vitality and height. It is uncertain if it is the resilience of the trees and/or their growth that act as a defense in these environments, but one can hypothesize that the suppressed height growth in these trials does not represent the full growth potential but is probably to a large extent a reflection of survival ability. This hypothesis is supported by our results for the type B correlations that showed stronger G × E for height, among trials with larger Tsum differences. Our results further showed that the sign of type AB genetic correlations between vitality and height changed from positive to negative in two of the trial series as the differences between Tsum of the trials increased, indicating that height in harsh environments reflects the health of the trees, as also expressed by the type A correlations, as suggested by Persson (2006).
In a bivariate simulation study including selectively deleted records, Persson and Andersson (2004) observed that comparing MV and UV analyses can result in an underestimation by 50% of type B genetic correlations if a UV model was used. In other crop-breeding simulations, Viana et al. (2010) detected that accuracies and efficiencies in family selection were greater with an MV REML model, compared with a UV model, while Holland (2006) found that when missing data are over 15%, an MV REML analysis showed better accuracies and estimates of genetic correlations. Ganesalingam et al. (2013) observed also greater accuracies in a bivariate survival study of blackleg disease, compared to a UV analysis. In our study, in general, \( {\widehat{h}}_w^2 \), \( {\widehat{h}}_b^2 \), and \( {\widehat{CV}}_A \) from UV MET analyses were overestimated, compared with those obtained through the MV MET analysis (Table S4 and Fig. S3), probably because the genetic correlation between vitality and height is not accounted for and less phenotypic information is evaluated in the UV MET analysis. Our study also agrees with others (Bauer and Leon 2008; Calleja-Rodriguez et al. 2019; Persson and Andersson 2004), reporting larger SE derived from the UV compared to the MV model.
Conclusions
Fitting factor-analytic structures in MV MET analysis allowed us to include up to 19 traits simultaneously, indicating that the factor-analytic approach should be applied routinely in analyses of multiple trials.
Trees in the harsh environments are still affected by environmental perturbations at 20 years of age, which in turn influences estimated genetic parameters. We have detected G × E for both vitality and height within trial series and that the difference in temperature sum between the trials was the main statistical driver for the noteworthy G × E.
Our findings are in agreement with earlier investigations and confirm that survival and tree growth should be given strong focus in the breeding of Scots pine in northern areas. We have observed a positive genetic association between tree vitality and height on harsh sites, which weakened as the temperature sum increased, suggesting that tree growth on harsh and mild sites ought to be treated as separate traits and targeted to different deployment regions.
References
Baltunis BS, Brawner JT (2010) Clonal stability in Pinus radiata across New Zealand and Australia. I. Growth and form traits. New For 40:305–322. https://doi.org/10.1007/s11056-010-9201-4
Baltunis BS, Gapare WJ, Wu HX (2010) Genetic parameters and genotype by environment interaction in radiata pine for growth and wood quality traits in Australia. Silvae Genet 59:113–124
Bärring L, Berlin M, Andersson Gull B (2017) Tailored climate indices for climate-proofing operational forestry applications in Sweden and Finland. Int J Climatol 37:123–142. https://doi.org/10.1002/joc.4691
Bauer AM, Leon J (2008) Multiple-trait breeding values for parental selection in self-pollinating crops. Theor Appl Genet 116:235–242. https://doi.org/10.1007/s00122-007-0662-6
Beeck CP, Cowling WA, Smith AB, Cullis BR (2010) Analysis of yield and oil from a series of canola breeding trials. Part I. Fitting factor analytic mixed models with pedigree information. Genome 53:992–1001. https://doi.org/10.1139/G10-051
Burdon RD (1977) Genetic correlation as a concept for studying genotype-environment interaction in forest tree breeding. Silvae Genet 26:168–175
Calleja-Rodriguez A, Li Z, Hallingbäck HR, Sillanpää MJ, Wu HX, Abrahamsson S, García-Gil MR (2019) Analysis of phenotypic- and estimated breeding values (EBV) to dissect the genetic architecture of complex traits in a Scots pine three-generation pedigree design. J Theor Biol 462:283–292. https://doi.org/10.1016/j.jtbi.2018.11.007
Chen ZQ, Harry BK, Wu HX (2017) Patterns of additive genotype-by-environment interaction in tree height of Norway spruce in southern and central Sweden. Tree Genet Genomes 13. https://doi.org/10.1007/s11295-017-1103-6
Cullis BR, Jefferson P, Thompson R, Smith AB (2014) Factor analytic and reduced animal models for the investigation of additive genotype-by-environment interaction in outcrossing plant species with application to a Pinus radiata breeding programme. Theor Appl Genet 127:2193–2210. https://doi.org/10.1007/s00122-014-2373-0
de la Mata R, Zas R (2010) Transferring Atlantic maritime pine improved material to a region with marked Mediterranean influence in inland NW Spain: a likelihood-based approach on spatially adjusted field data. Eur J For Res 129(4):645–658
Dieters MJ, White TL, Hodge GR (1995) Genetic parameter estimates for volume from full-sib tests of slash pine (Pinus elliottii). Can J For Res 25:1397–1408. https://doi.org/10.1139/x95-152
Eiche V (1966) Cold damage and plant mortality in experimental provenance plantations with Scots pine in northern Sweden. Stud For Suec 36:219
Ericsson T (1997) Enhanced heritabilities and best linear unbiased predictors through appropriate blocking of progeny trials. Can J For Res 27:2097–2101. https://doi.org/10.1139/cjfr-27-12-2097
Fries A (2012) Genetic parameters, genetic gain and correlated responses in growth, fibre dimensions and wood density in a Scots pine breeding population. Ann Forest Sci 69:783–794. https://doi.org/10.1007/s13595-012-0202-7
Ganesalingam A, Smith AB, Beeck CP, Cowling WA, Thompson R, Cullis BR (2013) A bivariate mixed model approach for the analysis of plant survival data. Euphytica 190:371–383. https://doi.org/10.1007/s10681-012-0791-0
Gezan SA, de Carvalho MP, Sherrill J (2017) Statistical methods to explore genotype-by-environment interaction for loblolly pine clonal trials. Tree Genet Genomes 13. https://doi.org/10.1007/s11295-016-1081-0
Gianola D, Norton HW (1981) Scaling threshold characters. Genetics 99:357–364
Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R (2015) ASReml user guide release 4.1 structural specification. VSN International Ltd, Hemmel Hempstead
Haapanen M (2001) Time trends in gentic parameter estimates and selection efficiency for Scots pine in relation to field testing method. For Genet 8:129–144
Hardner CM, Dieters M, Dale G, DeLacy I, Basford KE (2010) Patterns of genotype-by-environment interaction in diameter at breast height at age 3 for eucalypt hybrid clones grown for reafforestation of lands affected by salinity. Tree Genet Genomes 6:833–851. https://doi.org/10.1007/s11295-010-0295-9
Holland JB (2006) Estimating genotypic correlations and their standard errors using multivariate restricted maximum likelihood estimation with SAS Proc MIXED. Crop Sci 46:642–654. https://doi.org/10.2135/cropsci2005.0191
Hong Z, Fries A, Wu HX (2014) High negative genetic correlations between growth traits and wood properties suggest incorporating multiple traits selection including economic weights for the future Scots pine breeding programs. Ann For Sci 71:463–472. https://doi.org/10.1007/s13595-014-0359-3
Isik F, Holland J, Maltecca C (2017) Genetic data analysis for plant and animal breeding. Springer International Publishing, New York
Ivkovic M, Gapare W, Yang HX, Dutkowski G, Buxton P, Wu H (2015) Pattern of genotype by environment interaction for radiata pine in southern Australia. Ann For Sci 72:391–401. https://doi.org/10.1007/s13595-014-0437-6
Jansson G, Li BL, Hannrup B (2003) Time trends in genetic parameters for height and optimal age for parental selection in Scots pine. For Sci 49:696–705
Kelly AM, Smith AB, Eccleston JA, Cullis BR (2007) The accuracy of varietal selection using factor analytic models for multi-environment plant breeding trials. Crop Sci 47:1063–1070. https://doi.org/10.2135/cropsci2006.08.0540
Kelly AM, Cullis BR, Gilmour AR, Eccleston JA, Thompson R (2009) Estimation in a multiplicative mixed model involving a genetic relationship matrix. Genet Sel Evol 41:33. https://doi.org/10.1186/1297-9686-41-33
Kroon J (2011) Spatiotemporal patterns of genetic variation for growth and fertility in Scots pine. Swedish University of Agricultural Sciences, Department of Forest Genetics and Plant Physiology Vol 52. ISSN 1652-6880. ISBN 978-91-576-7596-5
Kroon J, Ericsson T, Jansson G, Andersson B (2011) Patterns of genetic parameters for height in field genetic tests of Picea abies and Pinus sylvestris in Sweden. Tree Genet Genomes 7:1099–1111. https://doi.org/10.1007/s11295-011-0398-y
Lambeth CC (1980) Juvenile-mature correlations in Pinaceae and implications for early selection. For Sci 26:571–580
Li YJ, Suontama M, Burdon RD, Dungey HS (2017) Genotype by environment interactions in forest tree breeding: review of methodology and perspectives on research and application. Tree Genet Genomes 13(60). https://doi.org/10.1007/s11295-017-1144-x
Loehle C, Namkoong G (1987) Constraints on tree breeding - growth tradeoffs, growth strategies, and defensive investments. For Sci 33:1089–1097
Mathew B, Holand AM, Koistinen P, Leon J, Sillanpaa MJ (2016) Reparametrization-based estimation of genetic parameters in multi-trait animal model using integrated nested Laplace approximation. Theor Appl Genet 129:215–225. https://doi.org/10.1007/s00122-015-2622-x
Meyer K (2009) Factor-analytic models for genotype x environment type problems and structured covariance matrices. Genet Sel Evol 41(21). https://doi.org/10.1186/1297-9686-41-21
Ogut F, Maltecca C, Whetten R, McKeand S, Isik F (2014) Genetic analysis of diallel progeny test data using factor analytic linear mixed models. For Sci 60:119–127. https://doi.org/10.5849/forsci.12-108
Olsson T, Ericsson T (2002) Genetic parameter estimates of growth and survival of Pinus sylvestris with mixed model multiple-trait restricted maximum likelihood analysis. Scand J For Res 17:103–110. https://doi.org/10.1080/028275802753626746
Pagliarini MK, Kieras WS, Moreira JP, Sousa VA et al (2016) Adaptability, stability, productivity and genetic parameters in slash pine second-generation families in early age. Silvae Genet 65:71–82. https://doi.org/10.1515/sg-2016-0010
Persson T (2006) Genetic expression of Scots pine growth and survival in varying environments. Dissertation. Swedish University of Agricultural Sciences
Persson T, Andersson B (2003) Genetic variance and covariance patterns of growth and survival in northern Pinus sylvestris. Scand J For Res 18:332–343. https://doi.org/10.1080/02827580310003993
Persson T, Andersson B (2004) Accuracy of single- and multiple-trait REML evaluation of data including non-random missing records. Silvae Genet 53:135–139. https://doi.org/10.1515/sg-2004-0024
Persson T, Ståhl EG (1993) Effects of provenance transfer in an experimental series of Scots pine (Pinus sylvestris L.) in northern Sweden. Swedish University of Agricultural Sciences, Department of Forest Yield Research, Report 35, p 92
Persson T, Andersson B, Ericsson T (2010) Relationship between autumn cold hardiness and field performance in northern Pinus sylvestris. Silva Fenn 44:255–266. https://doi.org/10.14214/sf.152
Perttu K, Morén A-S (1994) Regional temperature and radiation indices and their adjustment to horizontal and inclined forest land Stud For Suec vol 194
R Core Team (2014) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Ruotsalainen S, Persson T (2013) Scots pine – Pinus sylvestris. In: Mullin TJ, Lee SJ (eds) Best practices for tree breeding in Europe. Skogforsk (The Forestry Research Institute of Sweden), Uppsala, pp 49–63
Smith AB, Cullis BR (2018) Plant breeding selection tools built on factor analytic mixed models for multi-environment trial data. Euphytica 214(143). https://doi.org/10.1007/s10681-018-2220-5
Smith A, Cullis B, Thompson R (2001) Analyzing variety by environment data using multiplicative mixed models and adjustments for spatial field trend. Biometrics 57:1138–1147. https://doi.org/10.1111/j.0006-341X.2001.01138.x
Smith AB, Ganesalingam A, Kuchel H, Cullis BR (2015) Factor analytic mixed models for the provision of grower information from national crop variety testing programs. Theor Appl Genet 128:55–72. https://doi.org/10.1007/s00122-014-2412-x
Stefansson E, Sinko MJ (1967) Experiments with provenances of Scots pine with special regard to high-lying forests in northern Sweden. Stud For Suec 47:108
Ukrainetz NK, Yanchuk AD, Mansfield SD (2018) Climatic drivers of genotype-environment interactions in lodgepole pine based on multi-environment trial data and a factor analytic model of additive covariance. Can J For Res 48:835–854. https://doi.org/10.1139/cjfr-2017-0367
Viana JMS, Sobreira FM, de Resende MDV, Faria VR (2010) Multi-trait BLUP in half-sib selection of annual crops. Plant Breed 129:599–604. https://doi.org/10.1111/j.1439-0523.2009.01745.x
Warnes GR, Bolker B, Bonebakker L, Gentleman R, Huber W, et al (2016) Package “gplots”. http://cran.r-project.org
Xiang B, Li B, Isik F (2003) Time trend of genetic parameters in growth traits of Pinus taeda L. Silvae Genet 52:114–121
Zapata-Valenzuela J (2012) Use of analytical factor structure to increase heritability of clonal progeny tests of Pinus taeda L. Chil J Agric Res 72:309
Acknowledgements
We wish to express our gratitude to Fikret Isik, Greg Dutkowski, Gunnar Jansson, Zhi-Qiang Chen, and Arthur Gilmour for their valuable comments related to the statistical analyses. We also thank two referees for the journal whose suggestions greatly improved the manuscript. This study was partially supported by the 2nd Research School in Forest Genetics and Breeding at the Swedish University of Agricultural Sciences, including Knut and Alice Wallenberg Foundation, and Sweden’s innovation agency (Vinnova).
Data archiving statement
All phenotypic raw data are stored in DATAPLANâdatabase (http://www.plantplan.com/index.php/about-plantplan-genetics) and can be accessible upon request.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Communicated by J. Beaulieu
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic Supplementary Material
ESM 1
(PDF 490 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Calleja-Rodriguez, A., Andersson Gull, B., Wu, H.X. et al. Genotype-by-environment interactions and the dynamic relationship between tree vitality and height in northern Pinus sylvestris. Tree Genetics & Genomes 15, 36 (2019). https://doi.org/10.1007/s11295-019-1343-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11295-019-1343-8