Introduction

Fig. 1
figure 1

Comparison of the original Taylor rule and actual policy rate in the United States. Note: The figure plots the estimated policy rate in the United States based on the original Taylor rule, calibrated with parameters \(\alpha _\pi =0.5, \alpha _y=0.5\), against the actual policy rate set by the Federal Reserve. It illustrates the divergence between the rule’s prediction and the actual policy decision

Full size image

In the evolving current economic milieu, does the Taylor rule remain a reliable compass, especially for discerning investors? This study probes the potential necessity for alternative frameworks that could better serve the investment community. While the Taylor rule has historically been a linchpin in guiding monetary policy decisions, its pertinence is increasingly being challenged. Unconventional monetary strategies, such as the zero interest rate policy (ZIRP) and negative interest rate policy (NIRP), coupled with forward guidance communication, have become more prevalent since the global financial crisis (GFC). The rapid and coordinated international response to crises, as seen during the GFC and the Coronavirus Disease 2019 (COVID-19) pandemic, further underscores the globalization of monetary policy and the consequent need for more adaptable guiding principles. Empirical evidence suggests that the Taylor rule in its current form is not applicable to contemporary economic conditions. Even basic tools provided by institutions (e.g. Federal Reserve Bank of Atlanta, 2023), demonstrate divergence from the rule’s predictions (Fig. 1). Furthermore, in the case of Japan, which has pursued a longstanding ZIRP and quantitative easing (QE) policy, the Taylor rule has proven to be largely inapplicable in recent years (cf. Rhodes and Yoshino, 2017). In the context of the new financial landscape following the financial crisis, the primary motivation of this paper is to explore how to amend the Taylor rule and how to utilize it effectively.

Regarding how to amend the Taylor rule, the paper ultimately proposes the introduction of dynamic factor analysis (DFA) for cross-country panel data. Before delving into the details of the model, this paper provides an overview of previous research regarding Taylor rule modification. In the past, studies have introduced regime-switching models, particularly in Japan, to address the zero lower bound (ZLB) (e.g. Hayashi et al. 2013). However, these studies merely separate the ZIRP from conventional monetary policy, and with the introduction of NIRP by the European Central Bank (ECB) in 2012, such assumptions are no longer realistic. To incorporate a continuous discussion of NIRP, it is necessary to introduce state-space models, which have been employed in single-country studies.

The challenge in this paper is to extend the state-space model for the Taylor rule to a multicountry setting, as there are no existing models that accomplish this. The response functions in the Taylor rule for the gross domestic product (GDP) gap and inflation rate differ among countries, so the absence of panel data analysis in the literature is natural. This paper assumes international monetary policy coordination by introducing nonmacro factors and stationary correlations into the diffusion matrix, which typically assumes independent and identically distributed (IID) variables. These two classifications of variables distinguish between policy rate fluctuations that diverge from macroeconomic variables due to intentional central bank actions from those that occur inadvertently. If the nonmacro factors or residual’s correlations (or covariances) are nonzero, this model can capture previously undetected international monetary policy coordination.

Regarding the discrepancy between the policy interest rate estimated using the Taylor rule and the actual policy interest rate, previous research, such as Ueda (2005), Yellen (2004), and Blinder and Reis (2005), has suggested that discretionary and preventive responses by policymakers are likely to manifest as errors. In the context of globalization, there has been considerable coordination of monetary policies, and this paper aims to incorporate these qualitative phenomena into the model as a primary motivation and one of the objectives. This study conducted DFA and found that the model error correlation is quite large, indicating that discretionary and preventive decisions have been strongly emphasized in the policies of other central banks.

On the other hand, regarding the question of how to utilize it, the normative role of the Taylor rule undeniably remains pivotal for central banks. However, recent developments highlight an increasing need to grasp the evolution of its foundational assumptions, especially from a financial econometric perspective, since its origination. Furthermore, the profound comprehension of global interest rate policy has become paramount in asset management, notably due to the ascent of multi-asset investment and the macro-finance sphere. This study posits that deviations in the multicountry Taylor rule may be conceptualized as a global value factor, with transitory deviations from the principle anticipated to revert in a relatively swift manner, rendering this a plausible supposition. This study examines the pertinence of this factor premium in determining the viability of utilizing the deviation in the multicountry Taylor rule as a factor exposure within a macro-finance framework. The empirical analyses suggest that this factor exposure is salient for government bonds spanning maturities of 2, 5, and 10 years. In line with the pure expectations hypothesis, transient monetary interventions predominantly influence short-term expectations while having a negligible effect on long-term expectations. This phenomenon can likely be ascribed to the market’s perception of such policy shifts as ephemeral.

This study focuses on the monetary policy discussions of the Group of Seven (G7) advanced economies. While this represents an increase in the number of regions covered compared to multicountry dynamic stochastic general equilibrium models, which typically cover approximately three regions (e.g., the global multicountry model proposed by Albonico et al. (2019)), it does not comprehensively encompass global financial policies. In particular, central banks in emerging economies tend to take actions that deviate from recent macroeconomic and financial policy practices in advanced countries, such as raising interest rates for currency defense and exchange rate guidance (Engler et al., 2018).

In summary, this study makes three distinct contributions to the academic literature: First, through the implementation of a multicountry DFA, this study models the continuous and dynamic changes in policy response functions, including those within an NIRP environment. While a review of the literature identifies the recognition of regional and temporal variations in these policy response functions, the research presented here is among the first to comprehensively examine these variations across multiple countries. Second, a significant contribution is made by introducing nonmacro factors and stationary correlation into the diffusion matrix of the multicountry DFA, thereby enabling qualification of discretionary policy decisions and their international cooperation. While qualitative analyses have suggested that the monetary policies of advanced economies are clearly influenced by the Federal Reserve’s policy trends, there has been a lack of macroeconomic methodologies to quantitatively measure this idea. This approach fills this gap and provides a robust tool for quantifying international monetary policy coordination. Last, by interpreting errors as transitory factors, this paper demonstrates that they can be incorporated within the framework of global risk premia as a novel value factor. This contribution, which is primarily in the realm of macro-finance, opens new avenues for understanding and interpreting the impacts of these temporary factors. Taken together, these contributions broaden the understanding of policy responses across different economies and periods, offer a quantitative measure of discretionary policy decisions and their international monetary policy coordination, and introduce a new way of treating errors within the macro-finance framework.

Literature Review

This section undertakes a comprehensive review of the extant literature pertaining to the Taylor rule and its practical deployment in the sphere of monetary policy evaluation. First, the inaugural formulation of the Taylor rule is elucidated, delineating its foundational suppositions and resultant implications. Subsequently, the primary complexities and quandaries that surfaced during the implementation of the Taylor rule with empirical data are addressed. This includes the divergence of actual policy rates from those suggested by the rule and the role of policymaker discretion and proactive interventions. Thereafter, the discussion transitions to an exploration of the latest advancements in Taylor rule model configurations and their applications in the context of global risk premia.

Taylor Rule: Empirical Applications and Challenges

The Taylor rule is a simple and intuitive formula that relates the target short-term nominal policy interest rate to macroeconomic variables such as inflation and output. The original formula proposed by Taylor (1993) is denoted as follows. In this equation, \(i_t\) represents the target short-term nominal policy interest rate, \(\pi _t\) is the inflation rate over the previous four quarters, \(r^*_t\) is the equilibrium real interest rate, \(\pi ^*_t\) is the inflation target, \(y_t\) is the logarithm of real GDP, and \(\bar{y}_t\) is the logarithm of potential GDP. The coefficients \(\alpha _\pi \) and \(\alpha _y\) measure the responsiveness of the policy rate to deviations of inflation from its target and output from its potential, respectively:

$$\begin{aligned} i_t = \mathbb {E}_t[\pi _t + r^*_t + \alpha _\pi (\pi _t - \pi ^*_t) + \alpha _y (y_t - \bar{y}_t)]. \end{aligned}$$
(1)

Despite its simplicity and elegance, applying the Taylor rule to real-world data poses several challenges. One of the most prominent issues is the deviation of actual policy rates from the rule-implied rates. This deviation could be interpreted as a measure of monetary policy stance or stance deviation (Taylor, 1999a). A positive (negative) deviation indicates that monetary policy is tighter (looser) than what the Taylor rule prescribes.

Several factors may explain why actual policy rates deviate from rule-implied rates. One reason is measurement error or uncertainty in estimating the variables that enter the Taylor rule, such as inflation, the output gap, the equilibrium real interest rate, and the inflation target. Another reason is structural change or instability in the parameters of the Taylor rule over time or across countries. A third reason is discretion or judgment by policymakers who may deviate from a simple rule for various reasons, such as responding to other objectives or factors that are not captured by the rule.

One example of discretion or judgment by policymakers is preventive response or preemptive action. This refers to situations where policymakers adjust the policy rate more aggressively than what a simple rule suggests to prevent or mitigate potential risks or shocks to the economy. For instance, some studies have argued that the Federal Reserve lowered its policy rate by more than what the standard Taylor rule would imply in response to events such as the long-term capital management crisis in 1998 and the dot-com bubble burst in 2000-2001 (Blinder & Reis, 2005).

Additionally, two specific instances are noteworthy examples: the Federal Reserve conducted a preemptive interest rate cut in 2019, and in March 2020, in response to the burgeoning crisis triggered by the COVID-19 pandemic, it lowered interest rates prior to significant deterioration in the real economy. These examples illustrate that applying the Taylor rule to empirical data requires careful consideration of various factors and circumstances that may affect monetary policy decisions and outcomes. Moreover, they highlight that the Taylor rule is not a rigid formula or prescription but rather a benchmark or guideline that can help evaluate and compare different monetary policy regimes and strategies.

Table 1 Estimated parameters for the inertial rule from previous studies
Full size table

Refinement of the Taylor Rule Through Dynamic Expansion

When the nominal interest rate reaches zero or close to zero, the Taylor rule becomes inoperative and the central bank faces the ZLB. This section reviews recent approaches to modify the Taylor rule to accommodate the ZLB using different types of models.

This section refers to the discussion on the implementation of the ZLB prior to the introduction of NIRP, as detailed by Taylor and Williams (2010). Before the implementation of the ZLB, early research, exemplified by contributions in Taylor (1999a) and Fuhrer (1997), concentrated on rules that expanded upon the original Taylor rule. This can be represented as:

$$\begin{aligned} i_t = \mathbb {E}_t[\rho i_{t-1} + (1-\rho )(\pi _t + r^*_t + \alpha _\pi (\pi _t - \pi ^*_t) + \alpha _y (y_t - \bar{y}_t))]. \end{aligned}$$
(2)

The concept of inertia was incorporated into the dynamics of the interest rate through the application of a positive coefficient for the parameter \(\rho \), resulting in what was commonly referred to as an “inertial rule”. The inertial rule also allowed for the possibility of policy adjustments in response to anticipated future values, or lagged representations, of inflation and the output gap.

A wealth of prior research has estimated parameters for this inertial rule, as compiled in Table 1. The gathered data revealed substantial variation in estimated parameters across countries and periods, even before the GFC, when ZIRP became prevalent. Furthermore, these estimates diverged significantly from the parameters proposed by Taylor (1993, 1999b), as shown in Table 2 in this study.

In retrospect, the parameters proposed by Taylor (1993, 1999b) could be considered theoretically optimal within the domain of macroeconomics, rather than actual estimated values. This insight underscores the necessity of treating theoretical suggestions as guiding principles, while recognizing that real-world measurements may exhibit considerable variation.

Table 2 Suggested policy rule coefficients
Full size table

However after the GFC, ZIRP became prevalent, and numerous corresponding approaches have been proposed. One approach to model the ZLB was to apply regime-switching models to the Taylor rule, which allowed for discrete changes in the monetary policy regime depending on the state of the economy.

As a seminal example, Taylor and Williams (2010) proposed a formulation to incorporate the ZLB within the Taylor rule framework. This was expressed as:

$$\begin{aligned} i_t = \max \{0, \mathbb {E}_t[\rho i_{t-1} + (1-\rho )(\pi _t + r^*_t + \alpha _\pi (\pi _t - \pi ^*_t) + \alpha _y (y_t - \bar{y}_t))]\} \end{aligned}$$
(3)

For another practical example, Hayashi et al. (2013) innovatively employed a regime-switching structural vector autoregression (SVAR) model to analyze Japan’s enduring experience with QE. Furthermore, Hurn et al. (2022) introduced a smooth transition autoregressive model for the United States (U.S.) federal funds rate, which oscillated between a regime governed by the Taylor rule and a regime defined by the ZLB. Utilizing Bayesian estimation techniques, they discovered that the transition between these regimes was influenced by the inflation rate and output gap. Remarkably, they reported that their model adeptly captured the persistence of the ZLB regime and its consequential impacts on macroeconomic variables.

Another approach was to apply state-space models to the Taylor rule, which allowed for continuous changes in the latent variables that affect the monetary policy stance. For example, Lombardi and Zhu (2018) introduced a shadow policy rate (SPR) that measured the hypothetical level of the nominal interest rate if there were no ZLB. They estimated a state-space model for the U.S. SPR using high-frequency financial data and found that it could capture the unconventional monetary policy actions of the Federal Reserve during the ZLB period. They also reported that their SPR could be used to assess the stance of monetary policy and its transmission to other interest rates.

A third approach was to incorporate the term structure of interest rates into the Taylor rule to enable forward-looking expectations of future monetary policy actions. Bekaert et al. (2005) developed a new Keynesian model with a term structure channel that linked the short-term interest rate to long-term interest rates through expectations. He reported that by committing to keep the short-term interest rate at zero for a longer period than implied by a standard Taylor rule, the central bank could lower long-term interest rates and stimulate aggregate demand.

These approaches have illustrated some possible ways to modify the Taylor rule to accommodate the ZLB using different types of models. However, they also faced challenges and limitations, especially in response to unconventional monetary policies, such as NIRP and forward guidance.

Estimation Methods for the Natural Rate of Interest

This subsection reviews two general types of estimation methods for the natural rate of interest, which are essential for Taylor rule estimation alongside observable variables such as the nominal interest rate, GDP, and inflation rate. The first type employed time series techniques, such as Hodrick-Prescott (HP) filters, to extract the natural rate of interest from real interest rate trends. This approach often neglected the theoretical relationship between the natural rate and other economic variables. The second type, emphasizing theoretical underpinnings, used data beyond real interest rates and ensured consistency with economic theory. Prominent methods in this category included the Laubach and Williams (2003) and the Holston et al. (2017) models and DSGE models.

Sudo et al. (2018) compared DSGE and overlapping generations (OG) models, highlighting their respective advantages and disadvantages. The DSGE model captured various shocks’ effects on the natural rate of interest, while the OG model explicitly incorporated demographic changes. However, both required numerous assumptions and parameters. This study employed a time series approach, specifically, the classical and robust HP filter, which demonstrated stability during the COVID-19 crisis, unlike the unstable Holston et al. (2017) model.

Bond Value Factors in Global Risk Premia and Macro Factors

The sovereign bond value factor embodies a construct that encapsulates the deviation from the perceived fair value, leveraging this discrepancy as a metric of risk exposure within a cross-country context. Various methodologies have been proposed to quantify the fair value as a means to estimate sovereign bond value risk exposure, including yield spreads, real yields, term premia, and excess returns. Notably, the real yield, calculated by deducting the inflation rate from the nominal yield, has been extensively utilized as a substitute measure for a government bond’s fair value. This approach is held in high esteem, largely because it resonates with classical macroeconomic principles that underscore its effectiveness in reflecting the fair value.

One of the seminal papers that introduced bond value as a factor in asset pricing is Asness et al. (2013), who constructed a global multi-asset portfolio based on value and momentum. They defined bond value factor as the negative of the 5-year change in yields for 10-year government bonds and showed that bond value had a positive and significant effect on bond returns across countries and time periods. They also examined alternative measures of bond value, such as real yield (the 10-year government bond yield minus the inflation rate) and term spread (the difference between the yield on a 10-year government bond and a 3-month Treasury bill) and found that real yield had the highest factor return t-value among the three definitions.

Baltussen et al. (2021) extended the analysis of Asness et al. (2013) by using a more comprehensive dataset of 24 global factor premiums across four asset classes (equities, bonds, currencies, and commodities) from 1800 to 2016. They also used real yield as their preferred measure of bond value based on the Fisher equation or Fisher effect (the real interest rate equals the nominal interest rate minus the expected inflation rate). They assumed that the expected inflation rate was approximately equal to the most recent value and that real interest rates in all countries should be at the same level. They found that bond value was one of the most robust and consistent factors in explaining asset returns over time and across markets.

However, Borio et al. (2022) questioned the assumption that real interest rates in all countries should converge to a common level in equilibrium. They suggested that there were multiple determinants of real interest rates in addition to inflation expectations, such as productivity growth, demographics, preferences, financial development, and global imbalances. They empirically demonstrated that significant heterogeneity and persistence existed in real interest rates across countries over time, implying that there was no single global real interest rate.

In macro-finance, there is an area of research, known as the macro factor approach, that determines factors based on their economic variables to bolster this trend. For instance, Kaya et al. (2012) contemplated a model that explains the variations in long-term asset price returns using economic growth factors and inflation factors. However, the model was unable to accurately measure these return fluctuations.

Conversely, Ang and Ulrich (2012) demonstrated that the term structures of both real and nominal interest rates could largely be explained by a model based on the Taylor rule, incorporating factors such as output gaps and inflation. In particular, they showed that a significant proportion of the variation in the expected 10-year equity return could be attributed to changes in the output gap and inflation. While their empirical analysis was confined to the U.S., their quantitative examination of the impact of the macroeconomic environment on fluctuations in the prices of equities and government bonds is noteworthy.

Subsequently, Ito and Nakagawa (2018) employed a method reminiscent of the empirical testing in the Fama-French three-factor model (cf. Fama and French, 1993). They provided evidence of three common factors, interpretable as economic growth, the real interest rate, and inflation, across multiple asset classes such as equities in developed countries, real estate investment trusts, commodities, high-yield bonds, inflation-linked government bonds, and normal government bonds in developed countries. All of these macro factor studies corroborated that some or all of the three economic variables referenced by the Taylor rule (natural interest rate, inflation rate, and GDP gap) have explanatory power for the risk premia in government bonds and multiple asset classes.

Methodology

Data and Preprocessing

Data from G7 advanced economies were used: the U.S. (Federal Reserve, FED), Japan (Bank of Japan, BOJ), the Eurozone (European Central Bank, ECB), the United Kingdom (Bank of England, BOE), and Canada (Bank of Canada, BOC). The focus was on the inflation rates and economic growth rates that were considered by the central banks in each country as key indicators of monetary policy decisions. All data were obtained from Bloomberg (2023) and converted to quarterly frequency.

The sample period covered 1990Q1 to 2022Q4, but some countries had missing data in the early years. Therefore, the analysis was restricted to the period from 1999Q1 to 2022Q4, when all data were available for all countries. The potential growth rate (the long-term trend of economic growth) estimated by the HP filter was utilized as a proxy for the natural rate of interest. For a discussion of the natural rate of interest and its estimation methods, see the “Estimation Methods forthe Natural Rate of Interest” section. The HP filter is defined by the following equation:

$$\begin{aligned} \min _{\{g_t\}} \sum _{t=1}^T (y_t - g_t)^2 + \lambda \sum _{t=2}^{T-1} [(g_{t+1} - g_t) - (g_t - g_{t-1})]^2 \end{aligned}$$
(4)

where \(y_t\) is the observed time series (in this case, the economic growth rate), \(g_t\) is the trend component (the potential growth rate), T is the number of observations, and \(\lambda \) is a smoothing parameter that controls the degree of smoothness of the trend. For quarterly data, \(\lambda =1600\) is set, as suggested by Hodrick and Prescott (1997) and Ravn and Uhlig (2002).

The target inflation rates for each country were based on the official figures published by each central bank or compiled by the Japanese Cabinet Office. It was assumed that these target inflation rates are constant over time. The target inflation rates for each country are shown in Table 3.

Table 3 Inflation targets of various countries
Full size table

Model

In the “Taylor Rule: Empirical Applications and Challenges” subsection, the standard form of the Taylor rule is presented as

$$\begin{aligned} i_t = \mathbb {E}_t[ \pi _t + r^*_t + \alpha _\pi (\pi _t - \pi ^*_t) + \alpha _y (y_t - \bar{y}_t) ] \end{aligned}$$
(5)

where \(i_t\) is the nominal interest rate, \(\pi _t\) is the inflation rate, \(r^*_t\) is the natural real interest rate, \(\pi ^*_t\) is the target inflation rate, \(y_t\) is the output level, and \(\bar{y}_t\) is the potential output level. The coefficients \(\alpha _\pi \) and \(\alpha _y\) measure the responsiveness of the interest rate to deviations from target inflation and potential output, respectively.

To extend the Taylor rule to a multicountry setting with panel data, some notation was modified and some assumptions introduced. First, j is used to index countries instead of i, which could be confused with the interest rate. Second, a country-specific error term \(u_{t,j}\) is added to capture unobserved factors affecting the interest rate decision. It was assumed that \(u_{t,j}\) follows a normal distribution with mean zero and variance-covariance matrix \(\Sigma \). The multicountry Taylor rule can then be written as

$$\begin{aligned} i_{t,j} = \pi _{t,j} + r^*_{t,j} + \alpha _{\pi ,j} (\pi _{t,j} - \pi ^*_{t,j}) + \alpha _{y,j} (y_{t,j} - \bar{y}_{t,j}) + u_{t,j}, \quad u_t \sim \mathcal {N}(0, \Sigma ). \end{aligned}$$
(6)

Note that when this equation is estimated for countries other than the home country, \(\pi _{t,j} - \pi ^*_{t,j}\) and \(y_{t,j} - \bar{y}_{t,j}\) are set to zero by using dummy variables.

There are different methods to estimate this equation depending on the assumptions made about the parameters and the error term. If it is assumed that \(\alpha _{\pi ,j}\) and \(\alpha _{y,j}\) are constant and \(\Sigma \) is diagonal, ordinary least squares (OLS) can be used to separately estimate each country. If it is assumed that \(\alpha _{\pi ,j}\) and \(\alpha _{y,j}\) are constant and \(\Sigma \) is unconstrained, generalized least squares (GLS) can be used to account for heteroskedasticity and cross-country correlation. If it is assumed that \(\alpha _{\pi ,j}\) and \(\alpha _{y,j}\) are time-varying, a state space model for panel data (i.e., DFA) can be used to capture their dynamics, assuming that \(\Sigma \) is constant and not diagonal. This analysis employed the multivariate autoregressive state space (MARSS) model, a potent tool in the realm of DFA, to delineate the problem within the context of a state-space paradigm. The state-space model offers a robust structure for the analysis of dynamic systems, and the MARSS model provides a versatile tool for fitting these models.

The subsequent analysis will delve into the responses to the ZLB. The methodology proposed by Taylor and Williams (2010), as articulated in Eq. 3, holds merit. However, it fails to account for NIRP. Consequently, this study advocates for an asymmetric equation that can accommodate both negative interest rates and the ZLB, as delineated in Eq. 7. In this model, the higher value between the negative interest rate level at a specific point in time (denoted as \(i_{LB,t,j}\)) and the theoretical policy interest rate level as per the Taylor rule was employed. Here, \(TR_{t,j}\) signifies the theoretical value of the Taylor rule at time t:

$$\begin{aligned} {\begin{matrix} &{}i_{t,j} = \max \{i_{LB,t,j}, \mathbb {E}_t[TR_{t,j}]\}\\ &{}\Longrightarrow i_{t,j} = {\left\{ \begin{array}{ll} \mathbb {E}_t[TR_{t,j}] \quad \text {if} \quad \mathbb {E}_t[TR_{t,j}] \ge i_{LB,t,j} \\ i_{t,j} = i_{LB,t,j} \quad \text {otherwise}. \end{array}\right. } \end{matrix}} \end{aligned}$$
(7)

Given that \(i_{LB,t,j}\) cannot be observed directly, this paper suggests that it should be zero when NIRP is not in effect in the preceding period, and in case it is enacted, the lower bound is adjusted to the value from the preceding period:

$$\begin{aligned} i_{LB,t,j}:= {\left\{ \begin{array}{ll} 0 \quad \text {if} \quad i_{t-1,j} \ge 0\\ i_{t-1,j} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$
(8)

However, the condition \(\mathbb {E}_t[TR_{t,j}] \ge i_{LB,t,j}\) in Eq. 7 is not ideally suited for time axis policy or forward guidance, as under forward guidance, a central bank commits to maintain a prolonged zero interest rate to affect future expectations and lower long-term interest rates (cf. Woodford, 1999; Reifschneider and Williams, 2000; Ueda, 2005). Thus, a novel state variable, \(\gamma _t\), was introduced, which embodies the degree to which the policy interest rate is influenced by nonmacro factors, inclusive of the lower bound constraint. If \(\gamma _t=1\), the central bank is able to direct the policy interest rate in accordance with the theoretical value, unaffected by any nonmacro factors. Conversely, when \(\gamma _t=0\), the central bank is entirely subject to the impact of the lower-bound constraint. This includes an inability to increase interest rates early, as suggested by the Taylor rule, due to the effect of forward guidance (or time-axis policy) after the attainment of the lower interest rate bound. If estimated accurately, it is anticipated that \(\gamma _t\) would fall within the range of \(0 \le \gamma _t \le 1\). Additionally, it is posited that the policy reaction function itself, represented here as \(TR_{t,j}\), is subject to dynamic fluctuations over time. Therefore, the final proposed model is depicted in Eq. 9. For the sake of distinction, this model is henceforth referred to as the time-varying Taylor rule (TV-Taylor rule):

$$\begin{aligned} i_{t,j}= & {} (1-\gamma _{t,j}) i_{LB,t,j} \!+\! \gamma _{t,j} \mathbb {E}_t[TR_{t,j}] + u_{t,j} \nonumber \\= & {} i_{LB,t,j} + \gamma _t (\mathbb {E}_t[TR_{t,j}] - i_{LB,t,j}) + u_{t,j} \nonumber \\= & {} i_{LB,t,j} \!+ \gamma _{t,j}(\pi _{t,j} + r^*_{t,j} \!-\! i_{LB,t,j}) \!+ \gamma _{t,j}\alpha _{\pi ,t,j} (\pi _{t,j} \!- \pi ^*_{t,j}) +\! \gamma _{t,j}\alpha _{y,t,j} (y_{t,j} \!- \bar{y}_{t,j}) \!+ u_{t,j} \nonumber \\ u_t\sim & {} \mathcal {N}(0, \Sigma ). \end{aligned}$$
(9)

The model is delineated as follows. The vectors \(I_t\) and \(I_{LB,t}\) at time \(t\) are constructed as:

$$\begin{aligned} I_t = \begin{bmatrix} i_{1,t} \\ \vdots \\ i_{n,t} \end{bmatrix}, \quad I_{LB,t}= \begin{bmatrix} i_{LB,1,t} \\ \vdots \\ i_{LB,n,t} \end{bmatrix}. \end{aligned}$$
(10)

The model is then represented in state-space form using the following equations:

$$\begin{aligned} X_t= & {} X_{t-1} + w_t, \quad w_t \sim \mathcal {N}(0, \Omega ) \end{aligned}$$
(11)
$$\begin{aligned} I_t= & {} I_{LB,t}+Z_t X_t + u_t, \quad u_t \sim \mathcal {N}(0, \Sigma ). \end{aligned}$$
(12)

In these equations, \(X_t\) is the state variable, \(w_t\) is the state noise, which is assumed to follow a normal distribution with mean 0 and covariance matrix \(\Omega \), \(Z_t\) is the observation matrix, and \(u_t\) is the observation noise, which is also assumed to follow a normal distribution with mean 0 and covariance matrix \(\Sigma \). The matrix \(\Omega \) is a nonidentical, diagonal matrix, while \(\Sigma \) is distinguished as an unconstrained matrix. The state variable \(X_t\) is a \(3n\) vector, which is defined as follows:

$$\begin{aligned} X_t = \begin{bmatrix} \gamma _{1,t}\alpha _{\pi ,1,t} \\ \vdots \\ \gamma _{n,t}\alpha _{\pi ,n,t} \\ \gamma _{1,t}\alpha _{y,1,t} \\ \vdots \\ \gamma _{n,t}\alpha _{y,n,t}\\ \gamma _{1,t} \\ \vdots \\ \gamma _{n,t} \end{bmatrix}. \end{aligned}$$
(13)

Notably, the formulations delineated in Eqs. 9 and 12 are equivalent. The observation matrix \(Z_t\) is an \(n \times 3n\) matrix, which is defined as a horizontal binding of the diagonal matrices of \(\pi _{t,j} - \pi ^*_{t,j}\), \(y_{t,j} - \bar{y}_{t,j}\), and \(\pi _{t,j} + r^*_{t,j} -i_{LB,t,j}\) for \(j = 1, ..., n\), where \(n\) is the number of countries:

$$\begin{aligned} Z_t =&\left[ \begin{array}{cccccccc} \pi _{t,1} - \pi ^*_{t,1} &{} 0 &{} \cdots &{} 0 &{} y_{t,1} - \bar{y}_{t,1} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \pi _{t,2} - \pi ^*_{t,2} &{} \cdots &{} 0 &{} 0 &{} y_{t,2} - \bar{y}_{t,2} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \pi _{t,n} - \pi ^*_{t,n} &{} 0 &{} 0 &{} \cdots &{} y_{t,n} - \bar{y}_{t,n} \end{array} \right. \nonumber \\&\left. \begin{array}{cccc} \pi _{t,1} + r^*_{t,1} -i_{LB,t,1} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \pi _{t,2} + r^*_{t,2} -i_{LB,t,2} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \pi _{t,n} + r^*_{t,n} -i_{LB,t,n} \end{array} \right] . \end{aligned}$$
(14)

In this formulation, the state-space model encapsulates the dynamic interrelationships among the nominal interest rate, inflation rate, and natural real interest rate. The Kalman filter and the expectation maximization (EM) algorithm with MARSS modeling, implemented by Holmes et al. (2012, 2023), then facilitate estimation of the parameters of this model and inference about the underlying system. The detailed specifications of the software environment utilized for the analysis are comprehensively outlined in the Online Supplemental Appendix.

Factor Analysis and Global Risk Premium Verification

This section presents the verification of bond factors in the literature on global risk premia based on the classical cross-sectional regression methodology with GLS (cf. Cochrane, 2005). This methodology offers a robust technique for quantifying the risk premium and discerning its impact on asset returns while allowing for the possibility of correlated residuals. The mathematical framework employed in this study is encapsulated in the following equations:

$$\begin{aligned} r_{t,j} = \hat{\alpha _{j}}+\hat{\beta } F_{t,j} + \epsilon _{t,j}, \quad \epsilon _{t,j} \sim \mathcal {N}(0, \Sigma ). \end{aligned}$$
(15)

In Eq. (15), the variable \(r_{t,j}\) represents the excess return on sovereign bonds (i.e., similar to the return on bond futures) for individual countries. In this analysis, a specific focus is placed on 2-year, 5-year, and 10-year bonds. The term \(F_{t,j}\) denotes the factor exposure (or factor loading). In this context, whether the error term of the proposed model carries a global risk premium was tested, which means that in this case, \(F_{t,j}= u_{t-1,j}\). The coefficient \(\beta \) signifies the sensitivity to F, essentially representing the risk premium for a specific factor. If the estimated \(\hat{\beta }\) is significantly positive, it can be statistically concluded that a consistent risk premium exists for the factor exposure:

$$\begin{aligned} r_{t,j} := \left( i_{t-1,j} - i_{0,t-1,j}\right) \times \frac{T}{365} - d \times \left( i_{t,j} - i_{t-1,j}\right) . \end{aligned}$$
(16)

These equations use a set of specific variables. The variable \(r_{t,j}\) denotes the return of country \(j\) at time \(t\). The symbol \(i_{t,j}\) signifies the nominal interest rate for period \(t\) of country \(j\) at time \(t\). Similarly, \(i_{0,t,j}\) corresponds to the short-term interest rate for country \(j\) at time \(t\). The term \(T\) represents the return measurement period in days, which is quarterly in this context. Finally, \(d\) embodies the bond duration in years.

Results

Comparative Analysis of Multicountry Taylor Rule Models

In the preliminary phase of the empirical analysis, several models are compared, the specifics of which are presented in Table 4 and Fig. 2. Alongside the proposed model, four other models are evaluated. First, the classical Taylor rule, referred to as the naive Taylor rule, is examined, using both OLS and GLS estimation methods. The comparative analysis reveals that the GLS estimation results in a lower Akaike information criterion (AIC), indicating a better model fit. Moreover, the inertia rule generally exhibits superior performance in terms of the AIC than the naive Taylor rule. Notably, the OLS estimation of the classical inertia rule demonstrates statistically significant advantages. The proposed model, the TV-Taylor rule estimated via MARSS, exhibited good performance compared to its peer models, as indicated by it having the lowest AIC.

Table 4 Comparative in-sample regression results of models under examination
Full size table
Fig. 2
figure 2

Comparison of model estimates and actual rates for policy interest rates of G7 countries. Note: The figure above compares model estimates and actual rates for the policy interest rates of G7 countries. Data source: Bloomberg (2023)

Full size image

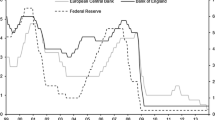
The subsequent analysis encompasses the calculation of the correlation matrix, derived from the residual matrix of the model proposed herein, revealing a notably high degree of error correlation, close to one in any pair (Fig. 3). Figure 4 illustrates the value of \(\gamma _t\), interpreted as the nonmacro factor, a construct introduced in the model. Additionally, Fig. 5 presents the correlation matrix for the first differentials of nonmacro factors, displaying positive correlations with the Fed, with the exception of the BOJ.

Fig. 3
figure 3

Estimated residuals (\(u_t\)) of the proposed model. Note: This figure presents the estimated TV-Taylor rule coefficient for the residuals \(u_t\) across G7 countries. Data source: Bloomberg (2023)

Full size image
Fig. 4
figure 4

Estimated Taylor rule coefficient for nonmacro factors (\(\gamma _t\)). Note: This figure presents the estimated TV-Taylor rule coefficient for the nonmacro factors across G7 countries. Data source: Bloomberg (2023)

Full size image
Fig. 5
figure 5

Correlation matrix for the first differentials of nonmacro factors (\(\Delta \gamma _t\)). Note: This figure presents the correlation of the first differentials of estimated TV-Taylor rule coefficient for the nonmacro factors across G7 countries. Data source: Bloomberg (2023)

Full size image

Assessment of Residuals as Potential Bond Risk Factors

In the second segment of the investigation, the aim is to ascertain whether the residual (\(u_{t,j}\)) in the TV-Taylor model holds the potential to function as a bond value factor. This objective was pursued through the use of GLS to estimate the regression in the “Factor Analysis and Global Risk Premium Verification” subsection, where \(r_{t,j}\) represents the excess return on investment three months prior, inferred from government bond prices:

The analytical outcomes are consolidated in Table 5. These empirical results facilitate the extraction of several salient observations: First, the coefficient of the residual (\(\hat{\beta }\)) was consistently positive and significant across all examined periods (2, 5, and 10 years). This lent credence to the notion that the residual might have functioned as a global risk exposure. Second, the coefficient of determination (\(R^2\)) for all periods was relatively low, suggesting that the explanatory power of the residual in terms of bond price movements or bond risk premia was somewhat limited. Third, the estimated \(\hat{\beta }\) approximated the asset’s duration.

Discussion

Interpretation of Results

The first experiment in the “Comparative Analysis of Multicountry Taylor RuleModels” section provided compelling evidence that the discretionary decisions of the central bank, previously perceived as deviation errors from the classical Taylor rule as outlined in Blinder and Reis (2005), are represented by nonmacro factors (\(\gamma _t\)) and model errors (\(u_t\)). These nonmacro factors embody intentional and discretionary policy rate changes initiated by the central bank, devoid of reactions to macroeconomic variables. On the other hand, the model errors (\(u_t\)) symbolize unintended policy rate changes by the central bank, such as the depletion of short-term liquidity during a credit crunch.

Several key interpretations emerge from this nonmacro factor estimation. First, in Japan, \(\gamma _t\) was consistently proximate to zero. The BoJ instituted a ZIRP in February 1999 that, with the exception of brief intermissions, has largely been maintained to the present, including the adoption of NIRP from 2016 onward. The narrative of intermittent deviations and recoveries in policy can be traced back to various key events. Initially, the information technology bubble economy of 2000 provoked a deviation from the policy, which was then restored after the bubble’s burst in 2001. However, a period of economic recovery in 2006 once again interrupted the policy. This interruption was short-lived, and the policy was reinstated in the midst of the 2008 GFC. This rendered the standard Taylor rule ineffective over a substantial duration, indicating a situation constrained to the lower bound as \(\gamma _t \approx 0\).

Table 5 GLS regression results: testing the significance of residuals as bond value factors
Full size table

Second, the Federal Reserve’s interest rate cuts beyond the scope of the Taylor rule since 2002, which were originally characterized as deviation errors from the Taylor rule by Blinder and Reis (2005), were represented in the model by a decrease in \(\gamma _t\) from 1. This suggests that the nonmacro factor aptly captures intentional deviations by the central bank from the Taylor rule as structural movements.

Third, following the collapse of Lehman Brothers in 2008 and the COVID-19 shock in March 2020, a significant dip in the nonmacro factors for central banks was observed in countries that had somewhat escaped from the ZLB at that time (i.e., countries where the nonmacro factor \(\lambda _t>0\). BOJ is excluded from this category, and ECB is an exception as of 2020). This dip signifies the implementation of internationally coordinated precautionary measures in response to the crisis.

Fourth, the global response to high inflation after 2021, brought on by the COVID-19 shock, was modeled as an elevation in the nonmacro factors rather than a shift in \(\alpha _\pi \). This mirrors the second observation, suggesting that the inflation issue became an international concern (a corollary of the global response to the COVID-19 crisis), resulting in an uncoordinated exit from the ZLB.

In contrast, the variable \(u_t\) signifies nonsystematic or unexpected shifts in the policy rate. Figure 3 exhibits considerable \(u_t\) volatility, illustrating the ripple effects of key financial events within and beyond the GFC. This pattern underscores the periods of acute liquidity crisis within the banking sector, which central banks combatted through the provision of liquidity supply facilities. The covariance matrix of \(u_t\) in Fig. 5 also indicates a high correlation, offering vital insights into the nature of 21st-century crises and their corresponding responses. Furthermore, the significant model error in the second experiment in the “Assessment of Residuals as Potential Bond RiskFactors” section suggests its potential utility as a novel bond value factor representing global risk exposure or unintended policy rate movements, although limited in scope.

Significance of Results

A noteworthy development is the adjustment of the Taylor rule to incorporate not only ZIRP, which can be addressed by a discrete regime-switching model, but also NIRP and forward guidance, which is a continuous transformation. Moreover, the proposed model accommodates a nonmacro factor and error correlations or, in a fundamental interpretation, unconventional monetary policy and international policy coordination, factors overlooked by conventional estimates for individual countries and the global Taylor rule model presuming IID conditions. The model also examines the quantitative differentiation of whether a change in the policy rate is a permanent or temporary measure, facilitating an applied discussion.

The introduction of dynamic policy response coefficients (\(\alpha _\pi , \alpha _y\)) and the novel nonmacro factor \(\gamma _t\) into the conventional Taylor rule validates the statistical efficacy of the proposed TV-Taylor rule. This adaptation is crucial, particularly considering the advent of ZIRP, NIRP, forward guidance, globalization of crises, and internationally coordinated responses in the 21st century.

Moreover, the ability to quantitatively differentiate between permanent, intentional policy rate decisions and temporary, unintentional fluctuations by central banks, offers robust applicability in relevant discussions. Furthermore, in asset management applications, the bond value factor may substitute for the global risk premium, especially for shorter maturities. This innovative approach forgoes the need for restrictive assumptions, such as the return of real interest rates to a constant international level, offering a more pragmatic alternative to traditional bond value factor applications.

Limitations of the Study

Despite these findings, certain limitations and areas for improvement remain. For instance, all results associated with the bond value factor are in-sample, which raises potential concerns that out-of-sample results might yield inferior outcomes. All the macro statistics in this study use finalized values but do not account for the lag in the release of these values. Additionally, although it is plausible to assume that the policy reaction function changes dynamically, it may not necessarily be rational to employ a basic random walk model for the state equation in this context.

Furthermore, Fig. 4 demonstrates that there are instances where \(0 \le \gamma _t \le 1\) is not satisfied. This is due to the MARSS algorithm being unable to impose such constraints, and it suggests that different results might be obtained if constraints were imposed.

Moreover, Fig. 2 indicates that the actual rate of the UK fluctuated against the guidance target in the beginning of 2000s. While such fluctuations could potentially be treated as noise, they are absorbed into \(\gamma _t\) in the model and interpreted as intentional policy interest rate guidance by the central bank. Although it is conventional in the estimation of the Taylor rule to use the actual rate, it may be possible to develop a model that better captures the intentions of the central bank, for example, by using the mid-value of the guidance target.

Unresolved Issues and Directions for Future Research

This section delineates problems that the study did not entirely resolve and presents novel questions for future researchers to explore. The exclusion of the consideration of the lag in the release of finalized macro-statistical announcements will be a challenge for devising investment strategies that actually utilize the error term of the proposed model as value premia. In practical applications, for instance, the model may need to be modified using leading indices, such as their forecasts, instead of coincident indices, such as GDP statistics or inflation rates.

Additionally, the G7 nations investigated in this study do not cover all major regions. Emerging economies such as China and India, which rank high in GDP, are omitted. It is anticipated that these regions do not necessarily conduct monetary policy in coordination with Western countries, and it is not always apparent whether monetary policy is conducted within the framework of the Taylor rule.

Furthermore, the fundamental interpretation that the current reasonable error against the Taylor rule is a discretionary and temporary (precautionary) measure is based only on somewhat dated studies such as Yellen (2004) and Blinder and Reis (2005). With the advent of large language models, it is now feasible to study whether individual rate cuts or hikes are temporary measures (cf. Hansen and Kazinnik, 2023). Such applied research should be a topic for future investigation.

Conclusion

This study reevaluates the Taylor rule in the context of modern monetary policy, acknowledging the growing divergence between traditional models and actual policy practice, particularly post-financial crisis. The Taylor rule is extended to a multicountry framework with cross-country panel data, introducing the novel TV-Taylor rule. This enhanced model incorporates a nonmacro factor and a dynamic approach to policy response coefficients, allowing for a nuanced understanding of unconventional monetary policies such as NIRP and ZIRP.

The analysis reveals the effectiveness of this model in capturing the nuances of international monetary policy coordination, emphasizing the importance of stationary correlation within a DFA. This study’s findings suggest that the model’s residuals could serve as indicators of global risk premia, particularly in the bond value factor, highlighting its utility in navigating complex monetary landscapes. This research contributes to the academic discourse by offering a robust framework that accommodates dynamic changes in policy response functions and aids in deciphering intricate global financial interactions.

In summary, this research not only redefines the Taylor rule to accommodate unconventional monetary policies, but it also demonstrates the potential of this framework to guide policy decisions and inform investors and asset managers. This study transforms the traditional rule into a versatile tool that can navigate the complexities of modern monetary strategies, highlighting its applicability beyond policymaking to serve as a reliable guide in the financial sector. Our work thus opens new avenues for applying the Taylor rule in a world where agile and globally coordinated monetary policies are increasingly vital.