Introduction and Motivation

The external imbalances among members of the European Monetary Union (EMU) during the pre-crisis period up to 2008 are empirically well-documented (e.g. Lane and Pels 2012). The huge external deficits in southern EMU countries (including Ireland = EMU “periphery”) are traditionally explained by intra-EMU factors: (i) financial integration and expectation of convergence within the common currency area, and (ii) “over-optimism” and excessive real appreciation in the periphery (e.g. Lane 2006). While accepting these traditional explanations, Chen et al. (2013) present new findings with respect to extra-EMU determinants, which contributed to the evolution of intra-EMU current account imbalances. Prominent among these are the trade linkages between the EMU sub-areas and the countries outside EMU, particularly China, the Central and Eastern European Countries (CEECs) and the oil exporting countries. This is true despite the entire EMU current account being roughly in balance. The periphery’s current account deficit, while financed mostly by capital inflows from the core, did not increase vis-à-vis the core but vis-à-vis Asia and oil exporters. A similar effect is also true with respect to the core current account surpluses. Moreover, financial integration between Asia and the U.S., albeit occurring under different institutional ramifications than those existing in the Eurozone, intensified after the East Asian currency crises in the late 1990s, as can be seen by the convergence of short-term nominal and real Asian and U.S. interest rates (Angeletos and Panousi 2011). Acknowledging both the strengthened real trade linkages of EMU sub-areas vis-à-vis Asia, and the closer financial linkages among Asia and the U.S.A., it is natural to suggest that the intra-EMU external imbalances are related to the external imbalances among Asia and the U.S. The main objective of this paper is to investigate whether this suggestion can be verified by use of an intertemporal current account model for the EMU, Asia and the U.S. (Obstfeld and Rogoff 1995 for the basic intertemporal current account model; Ca’Zorzi and Rubaszek 2012 for its empirical relevance for the Eurozone).

As is well-known, after the inception of the euro in 1999, northern and center euro countries (Austria, Belgium, Finland, France, Germany, Netherlands), particularly Germany, started to run current account surpluses, while the southern and western periphery (Portugal, Ireland, Italy, Greece and Spain = PIIGS) accumulated huge external deficits. Moreover, there was a significant divergence in the dynamics of private debt between northern and southern countries. Until the onset of the global financial crisis southern debt boomed, mainly in order to finance housing investment, while in the core, housing investment relative to gross domestic product (GDP) declined. In addition, saving rates in the periphery were significantly lower than those in the core. The mounting periphery current account deficits and core current account surpluses, were thus a logical consequence of the current account, simply being the difference between national savings and investment.

Although occurring under substantially different institutional ramifications, international macroeconomic developments similar to those in Europe emerged after the East Asian currency crises in the late 1990s between Asia and the U.S. While major Asian countries accumulated substantial external surpluses, the U.S. external deficit (current account and net foreign asset position) deteriorated significantly. In addition, private debt and housing investment in the U.S. boomed, while in Asia, housing investment as a proportion of GDP declined. Asian saving rates were also much higher than U.S. rates, resulting in U.S. current account deficits and Asian current account surpluses.

While such casual empirical similarities in the evolution of intra-EMU and Asia-U.S. (global) external imbalances are suggestive, it remains an open theoretical question, whether or how, divergent intra-EMU and Asia-U.S. external imbalances can be attributed to intra-EMU and Asia-U.S. financial integration in a dynamic general equilibrium model, of the world economy. To the best of these authors’ knowledge, the (at least) three-country intertemporal general equilibrium model needed to address both the intra-EMU and the Asia-U.S. external imbalances, does not yet exist in the literature. What do exist are dynamic general equilibrium models which deal with the intra-EMU or the Asian-U.S. external imbalances. Among the former are Fagan and Gaspar (2008) and Farmer (2014), and among the latter are Coeurdacier et al. (2015) and Eugeni (2015).

Fagan and Gaspar (2008) use a two-good, two-country overlapping generations pure exchange model to compare the pre-euro financial autarky steady state to euro-related financial integration between southern and northern euro countries. In view of the euro-related dynamics of housing investment in Spain and Ireland, Farmer (2014) sticks to Buiter’s (1981) seminal one-good, two-country overlapping generations (OLG) model with production and capital accumulation, and finds that the financial account deficits of EMU periphery and the respective surpluses of EMU core can be traced back, not only to core-periphery differences in time preference, but also to differences in the production technology (capital production share), government expenditure shares, and public debt to GDP ratios.

Regarding the Asian-U.S. external imbalances, Coeurdacier et al. (2015) also employ a one-good, two-country OLG model with three-person households and internationally diverging productivity growth rates. They find that the convergence of real interest rates between Asia and the U.S.A and the comparably large Asian productivity growth rates are accountable for Asian external surpluses and U.S. external deficits. Eugeni (2015) also uses a one-good, two-country OLG model in which the two countries are identical except that one country, i.e. the U.S., has a pay-as-you-go social security system, while the other country, i.e. China, does not. As a consequence of this institutional difference, the saving rates in the latter are significantly higher than in the former. Due to the largeness of the emerging economy, the world economy over-accumulates capital. The associated dynamic inefficiency of the world economy implies that the over-saving emerging country runs a surplus in the balance of trade. This is in line with the empirical findings for the East Asian countries.

Given the intensification of external trade following the euro launch, and the increasing financial integration between the U.S. and the East Asian countries, there now appears to be a need for the simultaneous investigation of intra-EMU and Asian-U.S. external imbalances. Moreover, since the EMU, East Asia and the U.S. are large open economies and are all affected by the impacts of intra-EMU and Asian-U.S. developments on trading partners, the international interdependences among EMU, Asia and U.S. need to be addressed. To this end, at a minimum, a three-good, three-country intertemporal equilibrium model is needed.

The paper thus has two main objectives: First, to present information regarding current and financial account imbalances between the EMU core and periphery, and between Asia and the U.S., in order to motivate model set-up. Second, to develop a three-country (EMU, Asia, U.S.), two-region (EMU core and periphery) OLG model in order to figure out the extent to which the EMU core-periphery as well as the Asian-U.S. external imbalances can be attributed to intra-EMU financial integration due to the common currency or to financial integration occurring between the U.S. and East Asia in the first decade of the new millennium.

Macroeconomic Findings: Financial Autarky versus Financial Integration

Following Fagan and Gaspar (2008, p. 9), the EMU countries are separated into two groups based on the differences in short-term real interest rates in the late 1990s, i.e. before the euro launch. The first group, usually denoted as the “core” countries, comprises the low interest rate countries of Austria, Belgium, France, Germany and the Netherlands.Footnote 1 The second group, denoted as “periphery” or converging countries, consists of countries which had relatively high interest rates before the introduction of the euro. In contrast to the pre-EMU situation (before 1999), EMU periphery’s higher real interest rates decreased towards lower rates in the EMU core (Farmer 2014, p. 5, Figure 2). Figure 1 shows a similar convergence of higher U.S. short-term real interest rates in the late 1990s towards the lower Asian rates, following the 1990s East-Asian currency crises (at the time of euro inception).

Fig. 1
figure 1

Real short-term interest rates in the U.S.A. and Asia 1990–2008. Source: World Bank (2014)

Full size image

Regarding differences in economic fundamentals, Farmer (2014, p. 6, Figure 3) portrays the existence of a substantially lower personal saving ratio (gross household savings as a percent of gross disposable income) in the EMU periphery than in the core since the euro launch. Similarly, Fig. 2 reveals that the U.S. personal saving rate is consistently substantially lower than the Asian rate, both in the 1990s and 2000s.

Fig. 2
figure 2

Asian and U.S. personal saving rates 1990–2008. Source: National Bureau of Statistics of China (2014), CEIC (2014), AMECO (2014), Bank of Korea (2014), FRED (2014)

Full size image

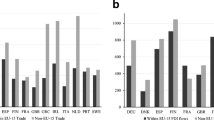
Starting from a significantly lower personal saving ratio in the EMU periphery relative to the core, housing investment expenditures in the periphery experienced a boom, while housing investment in the core countries declined. Through the sharp increase in private domestic expenditures in the periphery, and the muted response of output (Fagan and Gaspar 2008), current account balances in the periphery significantly deteriorated as shown in Fig. 3.

Fig. 3
figure 3

Current account balances (as a percent of GDP) in EMU periphery and core 1990–2008. Source: Updated and extended version of a dataset constructed by Lane and Milesi-Ferretti (2007)

Full size image

Not surprisingly, EMU periphery’s current account deficits led to the accumulation of a significant net foreign debtor position (Farmer 2014, p. 7, Figure 5). The differences with respect to the evolution of current account balances in Asia and the U.S.A. are portrayed in Fig. 4. Net foreign asset to GDP ratios are depicted in Farmer (2016, p. 387, Figure 2).

Fig. 4
figure 4

Current account to GDP ratios of Asia and the U.S.A. 1990–2008. Source: updated and extended version of a dataset constructed by Lane and Milesi-Ferretti (2007)

Full size image

Basic Model

Consider an infinite-horizon model economy consisting of three areas (“countries”) of the world economy, namely (i) the EMU, comprising two regions, named North (indexed by N) representing EMU’s core, and South (indexed by S), representing EMU’s periphery countries, (ii) the countries characterized by a current account surplus outside the EMU (indexed by A) representing Asia and oil-exporting countries, and (iii) the current-account deficit countries (indexed by U) representing mainly the U.S.A. In each country, one commodity, representing the aggregate of thousands of goods and services, is produced. This can be used for the purpose of consumption as well as for investment. The EMU specializes completely in the production of good X, Asia in the production of good Y, and the U.S.A. in the production of good Z. Perfectly competitive firms in the EMU’s South and North, in Asia and in the U.S. employ in every period t = 1 , 2 , … labor services \( {N}_t^i,\kern0.36em i= S, N, A, U \) and capital services \( {K}_t^i,\kern0.36em i= S, N, A, U \), using the Cobb-Douglas (CD) production function \( {M}^i{\left({a}_t{N}_t^i\right)}^{1-{\alpha}^i}{\left({K}_t^i\right)}^{\alpha^i}, i= S, N, A, U \), to produce southern (northern) EMU aggregate output \( {X}_t^S\left({X}_t^N\right) \), Asia’s aggregate output Y t and U.S. aggregate output Z t , where M i > 0 ,  i = S , N , A , U denote total factor productivity in EMU’s South (North), in Asia and in the U.S.A., respectively. a t is the common labor productivity and 0 < α i < 1 , i = S , N , A , U with α U ≈ α N < α S < α A are the capital production shares in EMU South, EMU North, Asia and in the U.S.A.

One-period profit maximization by firms in EMU’s South (North), in Asia and in the U.S.A. implies the following FOCs:

$$ {w}_t^i=\left(1-{\alpha}^i\right){M}^i{a}_t{\left({K}_t^i/{a}_t{N}_t^i\right)}^{\alpha^i}, i= S, N, A, U, $$
(1)
$$ {q}_t^i={\alpha}^i{M}^i{\left({K}_t^i/{a}_t{N}_t^i\right)}^{\alpha^i-1}, i= S, N, A, U, $$
(2)

whereby \( {w}_t^i, i= S, N, A, U \) denotes the real wage rate in each region and each country. \( {q}_t^i, i= S, N, A, U \) denotes real unit capital user costs in each region and each country i = S , N , A , U.

As usual in a Diamond (1965) type OLG framework, two generations of homogeneous individuals overlap in each period t. At date t, a new generation of size \( {L}_t^i \) enters the economy of country (region) i = S , N , A , U. For simplicity we assume that the population growth factors of all countries (regions) are identical and equal to G L. In view of the empirically rather similar GDP growth rates in southern and northern EMU countries (Fagan and Gaspar 2008), we assume that the respective growth factors of labor productivities \( {G}^{a^S} \) and \( {G}^{a^N} \) are equal in EMU’s South and North, an assumption which also applies rather well to the U.S.A., but rather less so to current-account surplus countries like China, India and other Asian countries. However, taking account of the catch-up growth component in emerging countries’ GDP growth rates, the simplifying assumption \( {G}^{a^S}={G}^{a^N}={G}^{a^U}={G}^{a^A}={G}^a \) seems acceptable. This implies that the natural growth factor G n = G a G L is the same in all countries.

Each generation lives for two periods, working during the first when young, and retiring in the second when old. The choice variables of each generation, when young, are denoted by superscript 1, and, when old, they are denoted by superscript 2. For each member of the generation entering the economy in period t, the supply of labor to firms is wage-inelastic since households attribute no value to leisure.

In order to describe the optimization problems of households more specifically, the institutional framework regarding international transactions across the three countries and across EMU core and periphery is now addressed. Regarding the three countries, we assume that each country has its own currency and that before the inception of the EMU, the southern and northern EMU member countries had their own currency, too. To mimic the period before the introduction of the common currency in 1999, we follow Gourinchas and Jeanne (2006), as well as Fagan and Gaspar (2008), and assume that before 1999, EMU’s South and North were financially autarkic. In contrast to the de-facto financial relationships among subsequent EMU countries, Asia and the U.S. existed before euro inception, so we also assume financial autarky for Asia and the U.S. in the pre-euro period. In contrast to financial autarky, we do, however, allow for trade relations later among EMU, Asia and U.S. during the pre-euro period, albeit on a moderate and balanced scale, thus mimicking mainly Japanese trade linkages vis-à-vis later EMU countries. The U.S., China and India did not play any important role in international trade during the pre-euro period.

Completely nominal, and to a lesser extent, real interest convergence across EMU’s South and North after the euro launch signifies financial integration across EMU’s South and North. This finding is portrayed in our intertemporal equilibrium model in line with Fagan and Gaspar (2008) as an equality of real interest rates of southern and northern EMU countries along the intertemporal equilibrium path. While by no means as complete as that within EMU, there is also, as Fig. 1 demonstrates, some real interest convergence or financial integration across Asia and the U.S.A. in the early 2000s. This supports our rather strong modeling assumption that after the euro launch, an uncovered parity condition, in terms of real interest rates, held across both Asia and the U.S. In line with Chen et al. (2013), internal investors from outside EMU invested their wealth in northern EMU financial assets. We also assume an uncovered real interest parity condition between the U.S. and EMU. In other words, after euro inception, financial integration prevailed worldwide but not as strictly as within the EMU.

In order to work out the consequences of intra-EMU, Asian and U.S. financial integration and the trade developments of EMU vis-à-vis non-EMU countries as clearly as possible, the optimization problems of (younger) households and firms as well as the market clearing conditions are now described separately for the cases of financial autarky and intra-EMU, Asian and U.S. financial integration.

Pre-Euro and Asian-U.S. Financial Autarky

To facilitate the modeling of the pre-euro situation as financial autarky, we first recall that southern EMU real interest rates were sizably larger than the corresponding northern rates. Second, in the 1990s EMU South (except Portugal) did not run large current account deficits (as a ratio of GDP). Hence, our modeling assumes that in the pre-euro period both the current account and the net foreign asset position of EMU South and North was zero. In contrast, in the 1990s, Asia (including oil exporters) ran current account surpluses (as a percent of GDP) roughly equivalent in size to the current account deficit of the U.S. However, since at this time the U.S. net foreign asset position was only moderately negative, and China and other emerging Asian countries did not contribute much to the imbalance, we assume that the U.S. and Asia were financially autarkic, just as the later EMU South and North were. Third, in contrast to the tremendous post-crisis accumulation of public debt, particularly in southern EMU, in Japan and in the U.S. in the 1990s and 2000s (up to 2008), the average debt to GDP ratios for EMU periphery, EMU core, and the U.S.A. remained constant over time or even receded slightly. In Asia (with the exception of Japan) public debt to GDP ratios decreased, and remained far below the EMU and U.S. ratios. We also assume that the (un-weighted) average of government debt to GDP ratios in Asia (including Japan) remains constant over time. Additionally, as Fig. 3 in Farmer (2014, p. 6) shows, after 1993 the personal saving rate in EMU South was lower than in EMU North. From Fig. 2 we know that Asia’s personal saving rate is significantly higher than the corresponding northern EMU rate, while the U.S. personal saving rate is slightly below the southern EMU personal saving rate.

In line with Chen et al. (2013) we accept that merchandise trade between EMU’s North and South was relatively modest after euro launch. We assume for the sake of simplicity that the same composite commodity is produced in North and South. Thus, while younger households in EMU South (North) cannot choose between consumption of domestic and northern (southern) commodities, they could buy Asian and U.S. goods in addition to the domestically produced good even before the euro launch.

Against this empirical background, the intertemporal utility maximization problem in EMU’s South later before euro inception (financial autarky) reads as follows:

$$ \begin{array}{l} \max \to {\zeta}^x \ln {x}_t^{S,1}+{\zeta}^y \ln {y}_t^{S,1}+{\zeta}^z \ln {z}_t^{S,1}+{\beta}^S\left({\zeta}^x \ln {x}_{t+1}^{S,2}+{\zeta}^y \ln {y}_{t+1}^{S,2}+{\zeta}^z \ln {z}_{t+1}^{S,2}\right)\hfill \\ {}\kern1.2em \mathrm{s}.\mathrm{t}.:\hfill \\ {}\kern1.2em (i)\kern0.48em {x}_t^{S,1}+\left(1/{e}_t^A\right)\;{y}_t^{S,1}+\left(1/{e}_t^U\right)\;{z}_t^{S,1}+{s}_t^S={w}_t^S\left(1-{\tau}_t^S\right),\mathrm{with}\ {s}_t^S\equiv {K}_{t+1}^{S, S}/{L}_t+{B}_{t+1}^{S, S}/{L}_t,\hfill \\ {}\kern1.2em \left( i i\right)\kern0.36em {x}_{t+1}^{S,2}+\left(1/{e}_{t+1}^A\right){y}_{t+1}^{S,2}+\left(1/{e}_{t+1}^U\right){z}_{t+1}^{S,2}={q}_{t+1}^S\left({K}_{t+1}^{S, S}/{L}_t\right)+\left(1+{i}_{t+1}^S\right)\left({B}_{t+1}^{S, S}/{L}_t\right).\hfill \end{array} $$

Here, 0 < β S ≤ 1 denotes the time discount factor of the (later) EMU’s southern younger generation, ζ k , k = x , y , z  with ζ x + ζ y + ζ z = 1 represents the utility elasticity of the consumption of good, k, \( {x}_t^{S,1} \) is the consumption per capita of the commodity produced in EMU’s South acquired at unit relative price, \( {y}_t^{S,1} \) is South’s consumption of the Asian good bought at the relative price of \( 1/{e}_t^A \), and \( {z}_t^{S,1} \) is southern consumption of the U.S. good acquired at the relative price of \( 1/{e}_t^U \). \( {e}_t^A \) denotes the units of Asian goods per unit of EMU goods (EMU terms of trade vis-à-vis Asia), while \( {e}_t^U \) portrays the units of U.S. goods per unit of EMU goods (EMU terms of trade vis-à-vis U.S.A.). \( {s}_t^S \) is South’s per capita savings, \( {\tau}_t^S \) denotes region South’s flat wage tax rate, \( {x}_{t+1}^{S,2} \) (\( {y}_{t+1}^{S,2},{z}_{t+1}^{S,2} \)) is old-age consumption per capita of the commodity produced in the South (Asia, U.S.A.), \( {K}_{t+1}^{S, S}/{L}_t^S \) is real capital produced in EMU South which the South’s younger households want to hold at the beginning of the retirement period, \( {B}_{t+1}^{S, S}/{L}_t^S \) stands for EMU South government bonds which South’s younger household wants to hold at the beginning of its retirement period, and \( {i}_{t+1}^S \) denotes the real interest rate on southern EMU government bonds. In line with pre-crisis empirical reality, the southern EMU young household invests its savings only in domestic real capital and government bonds. Constraint (i) depicts the working period budget constraint while constraint (ii) represents the retirement period budget constraint.

Analogously, the intertemporal utility maximization problem of the typical northern EMU household reads as follows:

$$ \begin{array}{l}\operatorname{Max}\to {\zeta}^x \ln {x}_t^{N,1}+{\zeta}^y \ln {y}_t^{N,1}+{\zeta}^z \ln {z}_t^{N,1}+{\beta}^N\left({\zeta}^x \ln {x}_{t+1}^{N,2}+{\zeta}^y \ln {y}_{t+1}^{N,2}+{\zeta}^z \ln {z}_{t+1}^{N,2}\right)\hfill \\ {}\kern2.16em \mathrm{s}.\mathrm{t}.:\hfill \\ {}\kern2.16em (i)\;{x}_{t\;}^{N,1}+\left({y}_t^{N,1}/{e}_t^A\right)+\left({z}_t^{N,1}/{e}_t^U\right)+{s}_t^N={w}_t^N\left(1-{\tau}_t^N\right),{s}_t^N\equiv \left({K}_{t+1}^{N, N}/{L}_t^N\right)+\Big({B}_{t+1}^{N, N}/{L}_t^N,\hfill \\ {}\kern2.16em \left( i i\right)\;{x}_{t+1}^{N,2}+\left({y}_{t+1}^{N,2}/{e}_{t+1}^A\right)+\left({z}_{t+1}^{N,2}/{e}_{t+1}^U\right)={q}_{t+1}^N\left({K}_{t+1}^{N, N}/{L}_t^N\right)+\left(1+{i}_{t+1}^N\right)\left({B}_{t+1}^{N, N}/{L}_t^N\right).\hfill \end{array} $$

Here, \( {x}_t^{N,1} \) (\( {y}_t^{N,1} \),\( {z}_t^{N,1} \)) stands for the purchases of later EMU (Asian, U.S.) goods by EMU North young households, and \( {s}_t^N,{\tau}_t^N,{K}_{t+1}^{N, N},{B}_{t+1}^{N, N} \) is interpreted in a similar fashion for the corresponding variables in EMU South.

The typical Asian young household solves the following optimization problemFootnote 2:

$$ \begin{array}{l}\operatorname{Max}\to {\zeta}^x \ln {x}_t^{A,1}+{\zeta}^y \ln {y}_t^{A,1}+{\zeta}^z \ln {z}_t^{A,1}+{\beta}^A\left({\zeta}^x \ln {x}_{t+1}^{A,2}+{\zeta}^y \ln {y}_{t+1}^{A,2}+{\zeta}^z \ln {z}_{t+1}^{A,2}\right)\hfill \\ {}\kern2.16em \mathrm{s}.\mathrm{t}.:\hfill \\ {}\kern2.16em (i)\;{e}_t^A\;{x}_{t\kern0.48em }^{A,1}+{y}_t^{A,1}+\left({e}_t^A/{e}_t^U\right){z}_t^{A,1}+{s}_t^A={w}_t^A\left(1-{\tau}_t^A\right),{s}_t^A\equiv \left({K}_{t+1}^{A, A}/{L}_t^A\right)+\left({B}_{t+1}^{A, A}/{L}_t^A\right),\hfill \\ {}\kern2.16em \left( i i\right)\;{e}_{t+1}^A{x}_{t+1}^{A,2}+{y}_{t+2}^{A,2}+\left({e}_{t+1}^A/{e}_{t+1}^U\right){z}_{t+1}^{A,2}={q}_{t+1}^A\left({K}_{t+1}^{A, A}/{L}_t^A\right)+\left(1+{i}_{t+1}^A\right)\left({B}_{t+1}^{A, A}/{L}_t^A\right).\hfill \end{array} $$

Here, \( {x}_t^{A,1} \) stands for the purchases (= consumption) of later EMU goods by Asian young households at the relative price of \( {e}_t^A \), while the purchase of U.S. products by Asian young households occurs at the relative price \( {e}_t^A/{e}_t^U \), i.e. units of Asian products per unit of U.S. goods. All other variables may be interpreted similarly to those in the EMU South’s young household optimization problem.

Finally, the typical U.S. young household faces the following optimization problem:

$$ \begin{array}{l}\operatorname{Max}\to {\zeta}^x \ln {x}_t^{U,1}+{\zeta}^y \ln {y}_t^{U,1}+{\zeta}^z \ln {z}_t^{U,1}+{\beta}^U\left({\zeta}^x \ln {x}_{t+1}^{U,2}+{\zeta}^y \ln {y}_{t+1}^{U,2}+{\zeta}^z \ln {z}_{t+1}^{U,2}\right)\hfill \\ {}\kern2.16em \mathrm{s}.\mathrm{t}.:\hfill \\ {}\kern2.16em (i)\;{e}_t^U\;{x}_{t\kern0.48em }^{U,1}+\left({e}_t^U/{e}_t^A\right){y}_t^{U,1}+{z}_t^{U,1}+{s}_t^U={w}_t^U\left(1-{\tau}_t^U\right),{s}_t^U\equiv \left({K}_{t+1}^{U, U}/{L}_t^U\right)+\left({B}_{t+1}^{U, U}/{L}_t^U\right),\hfill \\ {}\kern2.16em \left( i i\right)\;{e}_{t+1}^U\;{x}_{t+1\kern0.48em }^{U,2}+\left({e}_{t+1}^U/{e}_{t+1}^A\right){y}_{t+1}^{U,2}+{z}_{t+1}^{U,2}={q}_{t+1}^U\left({K}_{t+1}^{U, U}/{L}_t^U\right)+\left(1+{i}_{t+1}^U\right)\left({B}_{t+1}^{U, U}/{L}_t^U\right).\hfill \end{array} $$

Here, \( {x}_{t\kern0.48em }^{U,1} \) stands for U.S. young household’s purchases of the EMU product while \( {e}_t^U/{e}_t^A \) now indicates the units of the U.S. product, per unit of the Asian product which equals the relative price of U.S. consumption for the Asian good, \( {y}_t^{U,1} \).

The government of each country (region) i = S , N , A , U taxes labor income and uses revenues from additional borrowing to finance interest costs on existing government debt and government expenditures. The government budget constraint of country (region) i reads as followsFootnote 3:

$$ {B}_{t+1}^i-{B}_t^i+{\tau}_t^i{w}_t^i{L}_t={i}_t^i{B}_t^i+{\Gamma}_t^i, i= S, N, A, U, t=0,1,2,\dots, $$
(3)

where \( {\Gamma}_t^i \) denotes real government expenditures and \( {B}_t^i \) is the level of real government debt in country (region) i = S , N , A , U at the beginning of period t. In line with Diamond (1965), we assume that government expenditures are unproductive.

In addition to the restrictions imposed by household and firm optimization and by the above government budget constraints, markets for labor have to clear in all countries (regions) and in all periods.

$$ {N}_t^i={L}_t^i, i= S, N, A, U, t=0,1,2,\dots $$
(4)

Since the asset markets are competitive, transaction and adjustment costs do not occur and no risk (aversion) prevails, the following no-arbitrage condition (national Fisher equation) holds in all countries (regions):

$$ 1+{i}_{t+1}^i={q}_{t+1}^i+1-\delta, i= S, N, A, U,\kern0.36em t=0,1,2,\dots, $$
(5)

whereby 0 < δ ≤ 1 depicts the common fixed depreciation rate of private capital (period by period) in country (region) i.

The asset market clearing conditions in all countries (regions) are:

$$ {L}_t^i{s}_t^i={K}_{t+1}^i+{B}_{t+1}^i, i= S, N, A, U,\kern0.36em t=0,1,2,\dots, \kern0.5em \mathrm{and} $$
(6)
$$ {B}_t^i={B}_t^{i, i},{K}_{t+1}^i={K}_{t+1}^{i, i}, i= S, N, A, U,\kern0.36em t=0,1,2,\dots $$
(7)

Finally, the product markets in EMU, Asia and U.S. clear for all t = 0 , 1 , 2 , … according to the following conditions:

$$ \begin{array}{l}{X}_t^S+{X}_t^N={L}_t{x}_t^{S,1}+{L}_{t-1}{x}_t^{S,2}+{\Gamma}_t^S+{K}_{t+1}^S+{L}_t{x}_t^{N,1}+{L}_{t-1}{x}_t^{N,2}+{\Gamma}_t^N+{K}_{t+1}^N+{L}_t^A{x}_t^{A,1}+{L}_{t-1}^A{x}_t^{A,2}\hfill \\ {}+{L}_t^U{x}_t^{U,1}+{L}_{t-1}^U{x}_t^{U,2},\hfill \end{array} $$
(8)
$$ {Y}_t={L}_t^A{y}_t^{A,1}+{L}_{t-1}^A{y}_t^{A,2}+{\Gamma}_t^A+{K}_{t+1}^A+{L}_t{y}_t^{S,1}+{L}_{t-1}{y}_t^{S,2}+{L}_t{y}_t^{N,1}+{L}_{t-1}{y}_t^{N,2}+{L}_t^U{y}_t^{U,1}+{L}_{t-1}^U{y}_t^{U,2}, $$
(9)
$$ {Z}_t={L}_t^U{z}_t^{U,1}+{L}_{t-1}^U{z}_t^{U,2}+{\Gamma}_t^U+{K}_{t+1}^U+{L}_t{z}_t^{S,1}+{L}_{t-1}{z}_t^{S,2}+{L}_t{z}_t^{N,1}+{L}_{t-1}{z}_t^{N,2}+{L}_t^A{z}_t^{A,1}+{L}_{t-1}^A{z}_t^{A,2}. $$
(10)

In order to be able to model the fact of time-stationarity of country (region) i’s public debt to GDP ratios between 1999 and 2008, we transform total outstanding government debt in country (region) i’s government budget constraint into debt to GDP ratios. This is achieved by dividing both sides of (3) by X t   for  i = S , N, by Y t   for i = A, by Z t   for i = U, and by defining the debt to GDP ratios as \( {b}_t^i={B}_t^i/{X}_t^i, i= S, N \), \( {b}_t^A={B}_t^A/{Y}_t \), \( {b}_t^U={B}_t^U/{Z}_t \) we obtain for country i:

$$ {G}_t^{X, i}{b}_{t+1}^i=\left(1+{i}_t^i\right){b}_t^i+{\gamma}_t^i-{\tau}_t^i\left(1-{\alpha}^i\right),{G}_t^{X, i}\equiv {X}_{t+1}^i/{X}_t^i,{\gamma}_t^i\equiv {\Gamma}_t^i/{X}_t^i,{w}_t^i{L}_t/{X}_t^i=1-{\alpha}^i, i= S, N, $$
(11)
$$ {G}_t^Y{b}_{t+1}^A=\left(1+{i_t}^A\right){b_t}^A+{\gamma_t}^A-{\tau_t}^A\left(1-{\alpha}^A\right),{G}_t^Y\equiv {Y}_{t+1}/{Y}_t,{\gamma_t}^A\equiv {\Gamma_t}^A/{Y}_t,{w_t}^A{L}_t^A/{Y}_t=1-{\alpha}^A, $$
(12)
$$ {G}_t^Z{b}_{t+1}^U=\left(1+{i_t}^U\right){b_t}^U+{\gamma_t}^U-{\tau_t}^U\left(1-{\alpha}^U\right),{G}_t^Z\equiv {Z}_{t+1}/{Z}_t,{\gamma_t}^U\equiv {\Gamma_t}^U/{Z}_t,{w_t}^U{L}_t^U/{Z}_t=1-{\alpha}^U. $$
(13)

Dividing the asset market clearing condition (6) on both sides by \( {X}_t^i, i= S, N \), and using the definition of the capital output ratio \( {v}_t^i\equiv {K}_t^i/{X}_t^i, i= S, N \), (6) can be rewritten as follows:

$$ {G}_t^{X, i}{b}_{t+1}^i+{G}_t^{X, i}{v}_{t+1}^i={L}_t{s}_t^i/{X}_t^i={\sigma}^i\left(1-{\alpha}^i\right)\left(1-{\tau}_t^i\right),{\sigma}^i\equiv {\beta}^i/\left(1+{\beta}^i\right), i= S, N. $$
(14)

In view of the C-D production function, and noting \( {G}_t^{X, i}={\left({K}_{t+1}^i\right)}^{\alpha^i}{\left({a}_{t+1}{L}_{t+1}\right)}^{1-{\alpha}^i}/{\left({K}_t^i\right)}^{\alpha^i}{\left({a}_t{L}_t\right)}^{1-{\alpha}^i} \) \( =\left({a}_{t+1}{L}_{t+1}\right)/\left({a}_t{L}_t\right){\left({K}_{t+1}^i/{a}_{t+1}{L}_{t+1}\right)}^{\alpha^i}/{\left({K}_t^i/{a}_t{L}_t\right)}^{\alpha^i}, i= S, N \), it turns out that \( {G}_t^{X, i}={G}^n{\left({v}_{t+1}^i/{v}_t^i\right)}^{\alpha^i/\left(1-{\alpha}^i\right)} \).

Acknowledging that pre-crisis public debt to GDP ratios in all countries remained roughly constant over time, we assume time-stationary public debt to GDP ratios

$$ {B}_t^i/{X}_t^i={B}_{t+1}^i/{X}_{t+1}^i={b}^i,{b}^i>0, i= S, N,{B}_t^A/{Y}_t={B}_{t+1}^A/{Y}_{t+1}={b}^A,{b}^A>0,{B}_t^U/{Z}_t={B}_{t+1}^U/{Z}_{t+1}={b}^U,{b}^U>0. $$
(15)

Moreover, we assume time-stationary government expenditure shares:

$$ {\gamma}_t^i={\gamma}_{t+1}^i={\gamma}^i,\forall t,0<{\gamma}^i<1, i= S, N, A, U. $$
(16)

The government budget constraints, (11–13) together with (15) and (16) yield \( 1-{\tau}_t^i \) as follows:

$$ \begin{array}{l}1-{\tau}_t^i=\frac{1-{\alpha}^i-{\gamma}^i}{1-{\alpha}^i}+\frac{b^i}{1-{\alpha}^i}\left[{G}_t^{X, i}-\left(1+{i}_t^i\right)\right],\kern0.36em i= S, N,1-{\tau}_t^A=\frac{1-{\alpha}^A-{\gamma}^A}{1-{\alpha}^A}+\frac{b^A}{1-{\alpha}^A}\left[{G}_t^Y-\left(1+{i}_t^A\right)\right],\hfill \\ {}1-{\tau}_t^U=\frac{1-{\alpha}^U-{\gamma}^U}{1-{\alpha}^U}+\frac{b^U}{1-{\alpha}^U}\left[{G}_t^Z-\left(1+{i}_t^U\right)\right].\hfill \end{array} $$
(17)

Using the Cobb-Douglas production function it is easily seen that

$$ \begin{array}{l}{K}_t^i/{X}_t^i\equiv {v}_t^i=\left(1/{M}^i\right){\left[{K}_t^i/\left({a}_t{N}_t^i\right)\right]}^{1-{\alpha}^i}, i= S, N,{K}_t^A/{Y}_t^A\equiv {v}_t^A=\left(1/{M}^A\right){\left[{K}_t^A/\left({a}_t{N}_t^A\right)\right]}^{1-{\alpha}^A},\hfill \\ {}{K}_t^U/{Y}_t^U\equiv {v}_t^U=\left(1/{M}^U\right){\left[{K}_t^U/\left({a}_t{N}_t^U\right)\right]}^{1-{\alpha}^U}.\hfill \end{array} $$

Thus, the FOC for profit-maximizing capital service input (2) can be equivalently written as follows:

$$ {\alpha}^i/{v}_t^i={q}_t^i={i}_t^i+\delta, i= S, N, A, U. $$
(18)

In order to simplify the algebra, we assume δ = 1. Then, acknowledging (18) in (17) and considering \( {G}_t^{X, i}={G}^n{\left({v}_{t+1}^i/{v}_t^i\right)}^{\frac{\alpha^i}{1-{\alpha}^i}}, i= S, N\kern0.24em \left({G}_t^Y={G}^n{\left({v}_{t+1}^A/{v_t}^A\right)}^{\frac{\alpha^i}{1-{\alpha}^i}},{G}_t^Z={G}^n{\left({v}_{t+1}^U/{v_t}^U\right)}^{\frac{\alpha^i}{1-{\alpha}^i}}\right) \) yields:

$$ \left(1-{\tau}_t^i\right)\left(1-{\alpha}^i\right)=1-{\alpha}^i-\gamma +{b}^i{G}^n{\left({v}_{t+1}^i/{v}_t^i\right)}^{\alpha^i/\left(1-{\alpha}^i\right)}-{\alpha}^i{b}^i/{v}_t^i,\kern0.36em i= S, N, A, U. $$
(19)

The intertemporal equilibrium dynamics of the capital-output ratio in all countries (regions) is obtained by inserting (19) into (14):

$$ {\left({v}_{t+1}^i\right)}^{1/\left(1-{\alpha}^i\right)}+{b}^i\left(1-{\sigma}^i\right){\left({v}_{t+1}^i\right)}^{\alpha^i/\left(1-{\alpha}^i\right)}=\left({\sigma}^i/{G}^n\right)\left[1-{\alpha}^i-{\gamma}^i-\left({\alpha}^i{b}^i\right)/{v_t}^i\right]{\left({v_t}^i\right)}^{\alpha^i/\left(1-{\alpha}^i\right)}, i= S, N, A, U. $$
(20)

As usual, a steady-state intertemporal equilibrium is defined as a fixed point of the difference equation in (20): \( {v}_{t+1}^i={v}_t^i={v}^i, i= S, N, A, U \). Proposition 1 provides the existence conditions.Footnote 4

Proposition 1

(Existence of steady state solutions in country (region) i)

Suppose that \( 0<{b}^i\le {\overline{b}}^i<{\beta}^i\left(1-{\alpha}^i-{\gamma}^i\right)/{G}^n, i= S, N, A, U \) while \( {\overline{b}}^i \) solves β i(1 − α i − γ i) \( -{G}^n{\overline{b}}^i \) \( =2\sqrt{\alpha^i{\beta}^i\left(1+{\beta}^i\right){G}^n{\overline{b}}^i} \) . Then, there are exactly two strictly positive steady state solutions:

$$ {}_1 v_2^i={\left(2{G}^n\right)}^{-1}\left\{\left(1-{\alpha}^i-{\gamma}^i\right){\sigma}^i-\left(1-{\sigma}^i\right){b}^i{G}^n\mp \sqrt{{\left[\left(1-{\alpha}^i-{\gamma}^i\right){\sigma}^i-\left(1-{\sigma}^i\right){b}^i{G}^n\right]}^2-4{\alpha}^i{b}^i{G}^n{\sigma}^i}\right\}. $$
(21)

Since there are two steady-state solutions, (local) dynamic stability also needs to be investigated. This is done in proposition 2.Footnote 5

Proposition 2

(Dynamic stability of steady state solutions in country (region) i)

Suppose that \( 0<{b}^i<{\overline{b}}^i, i= S, N, A, U \) . Then, the steady-state solution \( {v}_1^i \) in (21) is asymptotically unstable while the steady-state solution \( {v}_2^i \) in (21) is asymptotically stable.

Knowing that the larger steady state solution in (21) is asymptotically stable, we use it to attribute the empirically observed pre-euro North-South, Asian and U.S. differences with respect to the real interest rates to EMU North-South, Asian and U.S. differences regarding fundamentals, including private saving rates, government expenditure ratios, capital production shares and government debt to GDP ratios. To this end, we first try to find out how the fundamental parameters impact the steady-state value of the capital-output ratio in (21). Second, we need information about the magnitudes of the saving rates, capital production shares, government expenditure quotas and public debt to GDP ratios in pre-EMU South and North, in Asia and in the U.S. Comparing pairwise the right-hand sides of (21) we are led to the following proposition.

Proposition 3

(Properties of financial autarky parameter sets)

Suppose that \( {b}^i<{\overline{b}}^i,\kern0.36em i= S, N, A, U \) and for simplicity b S = b N = b A = b U . If α S > α N , γ S ≥ γ N and σ S < σ N , then \( {v}_2^S<{v}_2^N \) implies i S > i N . Moreover, if α A > α U , γ A ≥ γ U and σ U < σ A , then \( {v}_2^U<{v}_2^A \) implies i U > i A .

The second step is to ensure that the assumptions behind proposition 3 are empirically warranted with respect to conditions prevailing in the three countries and two regions in the late 1990s. Both α S > α N and α A > α U are empirically warranted since capital production shares are larger in less developed countries and both the southern EMU and Asian countries are less developed (lower GDP per capita) than the northern EMU countries and the U.S. China, itself among the Asian countries, is a prominent empirical example of capital production share being higher in emerging than in more advanced countries, Bai and Qian (2010) on the high Chinese capital production share of nearly 50%, and Caselli and Feyrer (2007) on the much lower U.S. capital production share of 30%. In view of the empirical evidence provided by Figs. 2 and 3 in Farmer (2014, p. 6), it is natural to assume that σ S < σ N and σ U < σ A, i.e. that the saving rate of the southern EMU, is less than that of the northern EMU, and that the U.S. saving rate is smaller than the Asian saving rate.

Proposition 3 says that the relatively high capital production share and the low saving rate in EMU South imply under financial autarky that the steady-state capital output ratio in EMU South is lower than in EMU North, and is associated with a higher real interest in EMU South than in EMU North. Analogously, the significantly lower U.S. saving rate compared to the Asian saving rate implies, in spite of a higher Asian capital production share, a lower capital output ratio and a higher real interest rate in autarky. These claims are intuitively plausible. A low saving rate implies, for a given capital output ratio, low savings thus driving the capital output ratio down to ensure asset market clearing. The capital output ratio is also depressed by a relatively high capital income share since this implies a relatively low labor income share associated with low per capita savings. Due to decreasing marginal productivity of capital, the lower capital output ratio is associated with a higher interest rate.

Not surprisingly, under financial autarky the ratio of the net foreign asset position to GDP in country i = S , N , A , U defined as ϕ i = σ i[1 − α i − γ i − (α i b i)/v i] − G n[v i + b i(1 − σ i)] is zero. Using the budget constraints of young and old households plus the zero-profit and market clearing conditions, one can show that in steady state the current account to GDP ratio denoted as ca i , i = S , N , A , U and the trade balance to GDP ratio denoted as tb i , i = S , N , A , U are related to the respective net foreign asset to GDP ratio as follows: ca i = [(G n − 1)/G n]ϕ i and tb i = {[G n − (1 + i)]/G n}ϕ i. Clearly, both the current account and the trade balance to GDP ratio are zero in all countries (regions). Note, however, that balanced trade between EMU, Asia and the U.S.A. does not mean no trade at all. On the other hand, zero net foreign asset positions mean that no international borrowing and lending takes place in spite of the interest rate differential across countries. Obviously, the costs associated with shifting capital from the low-yielding EMU North and Asia, to the profitable EMU South and U.S.A., are prohibitively large. When modeling the advent of the common currency in Europe and financial integration between Asia and the U.S.A., we assume that these international capital mobility costs, i.e. the costs associated with exchange rate fluctuations in pre-euro countries, are completely removed overnight, while the structural parameters of all economies remain as assumed in proposition 3.

International Equilibrium under Intra-EMU and Asian-U.S. Financial Integration

To mimic the financial integration arising through the set-up of the EMU and the Asian-U.S. financial integration, we assume in line with the findings of Chen et al. (2013) that northern EMU invests its savings in southern physical capital and government bonds, that Asia buys U.S. government bonds, and that the U.S.A. purchases northern EMU government bonds without incurring any transaction costs. However, also in line with empirical data, we assume that the southern EMU young household does not buy northern real capital, northern government bonds, or Asian or U.S. assets.

Thus, the intertemporal optimization problem of the southern young household under financial integration is the same as under financial autarky. Analogously, the intertemporal utility maximization problem of the typical northern EMU household under financial integration is essentially similar to that under financial autarky with the exception of the investment of northern savings per capita and the old-age budget constraint which read now as follows: \( {s}_t^N\equiv {K}_{t+1}^{N, N}/{L}_t^N+{K}_{t+1}^{N, S}/{L}_t^N+{B}_{t+1}^{N, N}/{L}_t^N+{B}_{t+1}^{N, N}/{L}_t^N\;\mathrm{and}\ {x}_{t+1}^{N,2}+{y}_{t+1}^{N,2}/{e}_{t+1}^A+{z}_{t+1}^{N,2}/{e}_{t+1}^U={q}_{t+1}^N\left({K}_{t+1}^{N, N}/{L}_t^N\right)+ \) \( {q}_{t+1}^S\left({K}_{t+1}^{S, N}/{L}_t^N\right)+\left(1+{i}_{t+1}^N\right)\left({B}_{t+1}^{N, N}/{L}_t^N\right)+\left(1+{i}_{t+1}^S\right)\left({B}_{t+1}^{S, N}/{L}_t^N\right) \). Here, \( {K}_{t+1}^{S, N}/{L}_t \) and \( {B}_{t+1}^{S, N}/{L}_t \) denote the respective stocks of southern real capital and government bonds which the northern EMU young household wants to hold at the beginning of period t + 1. Since physical capital and government bonds in each EMU region are perfectly substitutable, the following international Fisher equation (real international interest parity condition) holds in addition to the national Fisher eqs. (5):

$$ 1+{i}_{t+1}^S=1+{i}_{t+1}^N. $$
(22)

Under financial integration the typical Asian young household essentially faces the same problem as under financial autarky. Now, however, the use of per-capita savings and the old-age budget constraint read as follows: \( {s}_t^A\equiv {K}_{t+1}^{A, A}/{L}_t^A+{B}_{t+1}^{A, A}/{L}_t^A+{e}_t^A/{e}_t^U{B}_{t+1}^{U, A}/{L}_t^A,{e}_{t+1}^A{x}_{t+1}^{A,2}+{y}_{t+2}^{A,2}+{e}_{t+1}^A{z}_{t+1}^{A,2}/{e}_{t+1}^U={q}_{t+1}^A{K}_{t+1}^{A, A}/{L}_t^A+\left(1+{i}_{t+1}^A\right)\left({B}_{t+1}^{A, A}/{L}_t^A\right)+\left(1+{i}_{t+1}^U\right)\left({e}_{t+1}^A/{e}_{t+1}^U\right)\left({B}_{t+1}^{U, A}/{L}_t^A\right). \) Here, \( {B}_{t+1}^{U, A}/{L}_t^A \) denotes the stock of U.S. government bonds which the Asian young household wants to hold at the beginning of period t + 1. In line with pre-crisis reality the Asian young household does not hold EMU government bonds. Analogously, savings per capita and the old-age budget constraint of the typical U.S. young household are as follows: \( {s}_t^U\equiv {K}_{t+1}^{U, U}/{L}_t^U+{B}_{t+1}^{U, U}/{L}_t^U+{e}_t^U\left({B}_{t+1}^{N, U}/{L}_t^U\right) \) and \( {e}_{t+1}^U\;{x}_{t+1\kern0.48em }^{U,2}+\left({e}_{t+1}^U{y}_{t+1}^{U,2}\right)/{e}_{t+1}^A+{z}_{t+1}^{U,2}={q}_{t+1}^U\left({K}_{t+1}^{U, U}/{L}_t^U\right)+\left(1+{i}_{t+1}^U\right)\left({B}_{t+1}^{U, U}/{L}_t^U\right)+\left(1+{i}_{t+1}^N\right){e}_{t+1}^U\left({B}_{t+1}^{N, U}/{L}_t^U\right). \) In line with pre-crisis empirical reality, the U.S. young household holds only northern EMU government bonds.

In order to ensure arbitrage-free terms of trade, the following international real interest parity conditions in addition to (22) ought to hold:

$$ 1+{i}_{t+1}^A=\frac{e_{t+1}^A}{e_t^A}\left(1+{i}_{t+1}^N\right),\forall t=0,1,2,\dots, $$
(23)
$$ 1+{i}_{t+1}^U=\frac{e_{t+1}^U}{e_t^U}\left(1+{i}_{t+1}^N\right),\forall t=0,1,2,.\dots $$
(24)

The markets for southern and northern EMU, Asian and U.S. real capital clear according to:

$$ {K}_{t+1}^S={K}_{t+1}^{S, S}+{K}_{t+1}^{S, N},{K}_{t+1}^N={K}_{t+1}^{N, N},{K}_{t+1}^A={K}_{t+1}^{A, A},{K}_{t+1}^U={K}_{t+1}^{U, U}, t=0,1,2.\dots $$
(25)

The markets for southern and northern EMU, Asian and U.S. government bonds clear according to:

$$ {B}_{t+1}^S={B}_{t+1}^{S, S}+{B}_{t+1}^{S, N},{B}_{t+1}^N={B}_{t+1}^{N, N}+{B}_{t+1}^{N, U},{B}_{t+1}^A={B}_{t+1}^{A, A},{B}_{t+1}^U={B}_{t+1}^{U, U}+{B}_{t+1}^{U, A}, t=0,1,2.\dots $$
(26)

The real interest parity (22) and the open real interest parity conditions (23) and (24) ensure that the worldwide amount of savings equals the worldwide supply of assets from the southern and northern EMU, Asia and the U.S. Thus:

$$ {L}_t{s}_t^S+{L}_t{s}_t^N+\frac{L_t^A{s}_t^A}{e_t^A}+\frac{L_t^U{s}_t^U}{e_t^U}={K}_{t+1}^S+{K}_{t+1}^N+{B}_{t+1}^S+{B}_{t+1}^N+\frac{K_{t+1}^A+{B}_{t+1}^A}{e_t^A}+\frac{K_{t+1}^U+{B}_{t+1}^U}{e_t^U}, t=0,1,2,.\dots $$
(27)

Finally, the product market clearing conditions are the same as under financial autarky.

Combining the solutions to the optimization problems of households and firms as well as the market-clearing conditions, the intertemporal equilibrium dynamics can be derived (Farmer and Ban 2014, pp. 22-25). It turns out that the intertemporal equilibrium dynamics consist of six non-linear first-order difference equations which can be used to determine the following six dynamic variables: \( {v}_t^S,{v}_t^N,{v}_t^A,{v}_t^U, \) \( {e}_t^A,{e}_t^U \).

In a steady state with \( {v}_{t+1}^S={v}_t^S={v}^S,{v}_{t+1}^N={v}_t^N={v}^N,{v}_{t+1}^A={v}_t^A={v}^A,{v}_{t+1}^U={v}_t^U={v}^U,{e}_{t+1}^A={e}_t^A={e}^A \) and \( {e}_{t+1}^U={e}_t^U={e}^U \), the system of first-order difference equations collapses onto an a-temporal system of six steady-state equations which can be used to determine the aforementioned six variables. Farmer and Ban (2014, pp. 25-26) show in their Proposition 4 that upper limits on public debt to GDP ratios in all countries similar to those in Proposition 1, ensure the existence of two non-trivial steady-state solutions for the northern EMU capital output ratios v N. Through the international real interest parity conditions v S = (α S/α N)v N , v A = (α A/α N)v N and v U = (α U/α N)v N, the capital output ratios of southern EMU, Asia and the U.S.A. are determined, while the EMU terms of trade with respect to Asia, e A, and with respect to the U.S.A., e U, follow from steady-state versions of the worldwide savings-investment equality (27) and ratios of the goods’ market-clearing conditions (8)-((10). Farmer and Ban (2014, p. 26) show, moreover, that for a broad set of structural and policy parameters the larger steady-state solution with respect to v N is saddle-point stable, while the smaller steady state is saddle-point unstable.

Financially Integrated versus Financially Autarkic Steady State

Knowing that under financial integration the larger steady-state solution is dynamically stable, proposition 4 can then be used to provide an answer to the main question of whether financial integration (i.e. the convergence of northern and southern EMU real interest rates and the presence of real open interest parity conditions across EMU, Asia and U.S.A.), contributes to the divergence of southern and northern EMU, Asia’s and U.S. trade balances, current account balances and net foreign asset positions.

Proposition 4

(Trade balance, current account and net foreign asset position effects of EMU and Asian-U.S. financial integration)

Suppose that the assumptions of proposition 3 hold, i.e. the southern EMU financial autarky (FA) interest rate, (i S)FA , is larger than the northern EMU financial autarky interest rate, (i N)FA , and the Asian financial autarky interest rate, (i A)FA is larger than the U.S. autarky interest rate (i U)FA . Suppose, moreover, that the structural and policy parameters of the three-country-three-good OLG model economy are such that in the financially integrated (FI) steady state the natural growth factor G n is larger than the common real interest rate, i FI . Then, the southern EMU and U.S. trade balance, current account and net foreign asset position to GDP ratios are negative, while the respective northern EMU and Asian ratios become larger than zero, i.e. (tb S)FI < 0 , (ca S)FI < 0 , (ϕ S)FI < 0  and (tb U)FI < 0 , (ca U)FI < 0 , (ϕ U)FI < 0 while (tb N)FI > 0 ,  (ca N)FI > 0 ,   (ϕ N)FI > 0 and (tb A)FI > 0 , (ca A)FI > 0 , (ϕ A)FI > 0.

Proof

By assumption, we have (i S)FA > (i N)FA  and (i U)FA > (i A)FA. Thus, 1 + (i S)FA =α S/(v S)FA > 1 + (i N)FA = α N/(v N)FA and 1 + (i U)FA = α U/(v U)FA > 1 + (i A)FA = α A/(v A)FA. Financial integration means that the difference between the southern and northern EMU, and between Asian and U.S. autarky interest rates diminishes as the southern EMU and the U.S. interest rate decline, and as the northern EMU and Asian interest rates rise. Due to the decreasing marginal productivity of capital, the decline in southern EMU and U.S. interest rates is associated with a rise in southern EMU and U.S. capital output ratios, and with a fall in northern EMU and Asian ratios. Recalling the definition of country’s i net foreign asset position in steady state as ϕ i(v i) ≡ σ i(1 − α i − γ i − α i b i/v i) − G n[v i + b i(1 − σ i)], differentiation of ϕ i with respect to v i yields ϕ i′(v i) = α i σ i b i/(v i)2 − G n. From proposition 2 in Farmer (2014) we know that there is a small neighborhood for country i’s autarky steady state with the larger capital output ratio, \( {v}_2^i \), in which \( {\phi}^{i\prime}\left({\left({v}_2^i\right)}^{FA}\right)<0 \) holds. Hence, country i’s net foreign asset position deteriorates with a rising capital output ratio, and improves with a declining capital output ratio. Since at the autarky value of \( {v}_2^i \) country i’s net foreign asset position is zero, and since the net foreign asset position of country i declines with rising capital output ratio at \( {\left({v}_2^S\right)}^{FI} \) and at \( {\left({v}_2^U\right)}^{FI} \), the southern EMU and U.S. net foreign asset positions are smaller than zero, i.e. \( {\phi}^S\left({\left({v}_2^S\right)}^{FI}\right)<0 \) and \( {\phi}^U\left({\left({v}_2^U\right)}^{FI}\right)<0 \). At the same time, at \( {\left({v}_2^N\right)}^{FI} \) and \( {\left({v}_2^A\right)}^{FI} \), the northern EMU and the Asian net foreign asset positions must be larger than zero, i.e. \( {\phi}^N\left({\left({v}_2^N\right)}^{FI}\right)>0 \) and \( {\phi}^A\left({\left({v}_2^A\right)}^{FI}\right)>0 \). Due to the steady state relationship of the trade balance and the current account balance with respect to the net foreign asset position, i. e. (tb i)FI = {[G n − (1 + i FI)]/G n}(ϕ i)FI and (ca i)FI =[(G n − 1)/G N](ϕ i)FI, and given the assumption of dynamic inefficiency (G n > 1 + i FI), southern EMU and U.S. trade and current balances become negative, while northern EMU and Asian trade and current account balances become positive.

A Numerical Illustration

Before concluding, a numerical specification of our three-country OLG is used to illustrate both its explanatory power and limitations. The following parameter values are chosen such that the model is able to roughly reproduce the main findings listed under financial autarky, and to accord with the assumptions in the earlier propositions presented. G n = 2,ζ x = 1/2 , ζ y = 1/4 , ζ z = 1/4 , β s = 0.45 , β N = 0.5 , β A = 0.6 , β U = 0.42 , α S = 0.17 , α N = 0.16, α A = 0.18 , α U = 0.16 , γ S = 0.17 , γ N = 0.2 , γ A = 0.18 , γ U = 0.15 , M S = 1 , M N = 1.5 , M A = 1 , M U= 1.5 , L S = L N = 85 , L A = 1300 , L U = 1350 , b S = 0.027 , b N = 0.023 , b A = 0.015 , b U = 0.025.

Table 1 reports the steady state values of the main endogenous variables in EMU South, EMU North, Asia, and in the U.S. under financial autarky (for the 1990s).

Table 1 Main endogenous variables in the EMU South, EMU North, in Asia and in the U.S. (calculated on a yearly basis) under financial autarky for the 1990s
Full size table

Note that the yearly real interest rates in EMU South, North, Asia and the U.S. exhibited in Table 1 are not too far from the real interest rates in the late 1990s (Farmer 2014, p. 5, Figures 1 and 2). Moreover, the assumption of financial autarky which implies zero current account and net foreign asset to GDP ratios for EMU South, EMU North, Asia and U.S. is roughly in accordance with the empirical data for the late 1990s, as can be seen from Figs. 3 and 4, (Farmer 2014, p. 7), Figure 5, and in Farmer (2016, p. 387, Figure 2).

Comparing the results in Table 2 to those in Table 1 reveals both satisfactory and non-satisfactory data. Regarding the satisfactory results, first we observe, through financial integration (equalization of real interest rates across the EMU, Asia and U.S.), the capital output ratio both in the EMU South and U.S. increases while it decreases in the EMU North and in Asia in line with empirical observations. Second, the common real interest rate is significantly lower than the autarky real interest rate in EMU South and in U.S. and higher than the autarky real interest rate in EMU North and Asia, also in line with empirical findings. Third, the net foreign asset to GDP ratios, exhibited in the fifth column of Table 2, are rather close to those previously reported in Farmer (2014, p. 7, Figure 5) and in Farmer (2016, p. 387, Figure 2).

Table 2 Main endogenous variables in the EMU South, EMU North, in Asia and in U.S.A. (calculated on a yearly basis) under financial integration (1999–2008)
Full size table

Regarding the unsatisfactory results, we observe from Table 2 that the current account to GDP ratios are too small in comparison with Figs. 3 and 4. This is particularly true with respect to the U.S. current account to GDP ratio.

Summary and Conclusion

This paper explores, within a three-good, three-country OLG model with production, capital accumulation and public debt, the convergence of high real interest rates towards lower rates and the emergence of external imbalances between both EMU core and periphery, and between Asia and the U.S., for the period between post inception of the common currency and onset of the global financial crisis in 2008. It also models the pre-euro situation and Asian-U.S. financial relations in the 1990s in terms of financial autarky, and the intra-EMU and the Asian-U.S. financial linkages in the 2000s in terms of financial integration, characterized by convergence of real interest rates across EMU, Asia and the U.S.

At steady states under conditions of financial autarky, a lower saving rate, a higher capital production share, and a higher debt to GDP ratio in EMU South were shown to comply with the empirical discrepancy between southern (high) and northern (low) EMU real interest rates and zero external imbalances across EMU South and EMU North before the advent of the common currency. Similarly, a much lower U.S. saving rate compared to the Asian saving rate, together with a relatively higher U.S. public debt to GDP ratio, was associated with a higher U.S. real interest rate compared to Asia, in spite of the relatively higher Asian capital production share prevailing before Asian-U.S. financial integration beginning in the 2000s.

After the inception of the common currency, free real capital mobility among EMU South and North led northern EMU households facing initially relatively high southern EMU interest rates to invest their wealth in southern EMU housing and residential objects. Free financial capital mobility after the East-Asian currency crises led Asian households facing initially relatively high U.S. interest rates to buy U.S. government bonds. As a consequence, southern EMU and U.S. interest rates fell, and northern EMU and Asian interest rates rose. Simultaneously, southern EMU and U.S. capital output ratios increased, while northern EMU and Asia’s capital output ratios decreased, inducing a negative net foreign asset position in (relatively low saving) southern EMU and in the U.S., and a positive net foreign asset position in (relatively high saving) northern EMU and Asia.

Associated with the southern EMU and U.S. net foreign debtor position, the southern EMU and U.S. current account became negative due to the higher interest payments needed on net foreign debts while the opposite held true with respect to the northern EMU and Asia’s current account surplus. In addition, southern EMU and U.S. current account deficits also occurred due to trade balance deficits as a result of increased (net) imports from Asia, while northern EMU and the Asian trade balances turned positive as a result of increased net exports to Asia and to the U.S., conforming to Chen et al. (2013). However, southern EMU and U.S. trade balance deficits vis-à-vis net foreign debts, and northern EMU and Asia’s trade balance surpluses vis-à-vis net foreign credits, can only emerge under conditions of dynamic inefficiency in the world economy.

In our large, open model, economy dynamic inefficiency does not result from the assumptions employed, but from the impact of high saving rates in Asia and in northern EMU in comparison to the low saving rates in the U.S. and southern EMU economies, together with the impact of the further international differences in capital production shares, government expenditure and public debt ratios as stated in proposition 3. High Asian saving rates together with the other international differences in structural and policy parameters, led, via the dynamic inefficiency of the whole economic system, to the empirically observed trade balance surpluses of northern EMU and of Asia, as well as to the trade balance deficits of southern EMU and of the U.S. Thus, once the intensified trade linkages of EMU South and North vis-à-vis Asia after the euro launch are taken into account, and once the high Asian saving rates following from the East-Asian currency crises are considered, we conclude that a more correct modeling of pre-crisis intra-EMU external imbalances triggered by euro-related financial integration requires that the financial integration between Asia and the U.S.A. also be taken into account. However, future research will demonstrate whether this conclusion remains true if more general utility and production functions than our logarithmic utility and Cobb-Douglas production function are used to derive our main Proposition 4.