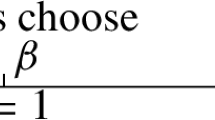Introduction

Early literature on strategic team behavior has considered teams’ decisions as optimal and proceeded to analyze how those choices are affected by rule changes.Footnote 1 More recently, there has been an increase in research about whether a team’s and athletes’ behavior are in fact consistent with predictions from game theoretical models. Divergence from optimal play has been documented with explanations often deriving from cognitive psychology. Cohen-Zada et al. (2017) showed that professional tennis players underperform at the most important junctures of the match, explaining it as the phenomenon of choking under pressure. Also using data from tennis, Cohen-Zada et al. (2018) showed that the order of actions in a tiebreaker game has an important effect in eliminating the ahead-behind asymmetry. Bar-Eli et al. (2007) documented that goalkeepers in soccer penalty kicks have a strong propensity to jump and avoid staying at the center of the goal, demonstrating an action bias.

With more focus on coaches’ strategies, Lefgren et al. (2015) found outcome bias in their study of decision making in professional basketball. They showed that coaches in the National Basketball Association (NBA) change their starting lineup more often after narrow losses than after narrow wins. That is indicative of their decisions being evaluated more favorably in light of a positive outcome than a negative outcome leading to a stronger reaction even if facing similar circumstances. Meier et al. (2023) extended their analysis and confirmed that result for women’s professional basketball, men’s and women’s college basketball, and the National Football League (NFL). In literature with a stronger theoretical component, Romer (2006) used the NFL to examine a team’s decision whether to kick the ball on fourth down or try to obtain a first down instead. After calculating the expected value in each situation, he concluded that in most cases teams would maximize their probability of winning the game by going for a first down, but instead almost always kick the football. In the analysis, only two possible strategies were considered and team heterogeneity was not allowed. Finally, Santos (2014) presented a model where the strategy set allowed for a continuum of possible choices, while still including asymmetric considerations among teams. However, in his model there were only two periods in the analysis, thus leading to the unrealistic scenario where coaches are only making decisions at two different moments in a game. Santos used the model to show that soccer coaches appear to adopt more defensive strategies than optimal.

The current paper presents a model that permits evaluation of the impact of different team strategies (behavior) on the expected game results (outcome). Comparing those model predictions to those observed from coaches in real life scenarios permits determination of whether these highly paid professionals are deciding optimally or if instead their decisions are not rationalizable. The model proposed can be applied to nearly every sport, and allows for a richer dynamic element in the analysis compared to the work of Santos (2014). Coaches can make decisions at any possible number of moments in the game (T), not just two. Team and game characteristics, such as where the game is played (home or away), and the strength of the teams involved (their quality) are also included in the analysis. Finally, the set of possible coaching strategies is a continuum of alternative choices and not restricted to just two as in Romer (2006). Those three conditions mimic more realistically the setting that sports’ coaches face during games, and thus provide the proper framework to then evaluate whether those coaches’ decisions are optimal or not.

Model

There are two risk-neutral teams (\(i,-i\)) whose objective is to maximize the number of points obtained in each match. Teams get \(x\) points per victory, \(z\) when they draw and 0 if they lose. Teams’ choice variable is the degree of offensive play they will present in each period of the game (\({\theta }_{t}^{i}\)), where \(t\in \left\{\mathrm{1,2},...,T\right\}\) denotes the period of the game.Footnote 2 Let \(\theta \in \theta\) be a compact set. Denote \({S}_{t}^{i}\) as the number of goals/points team (\(i\)) scores in period (\(t\)), with \(S\in P = \left\{-\widehat{P},...,-\mathrm{1,0},1,...,\widehat{P}\right\}\) where \(\widehat{P}\) is the maximum number of goals/points scored or conceded per period. Let \({\Delta }_{t} \in P\) identify the point difference at the beginning of period \(t\). If \({\Delta }_{t}>(<) 0\), team \(i(-i)\) is leading the score, and both teams are tied if \({\Delta }_{t}=0\). When the game begins with a tie, \({\Delta }_{1}=0\) but for any other period of the game \({\Delta }_{t}={S}_{t-1}^{i}-{S}_{t-1}^{-i}+ {\Delta }_{t-1}\). There are many possible events in each half depending on the number of points scored by each team. The outcomes \(\left({S}_{t}^{i} - {S}_{t}^{-i}\right)\) depend on the degree of offensive play each team chooses in each period since the probabilities of scoring points are affected by those decisions. Let \({\gamma }_{t}^{i}\left(S|X\right)\) be the probability that team \(i\) scored \(S\) points in period \(t\), given a vector of independent variables \(X\). These variables are the strategy pair \(\left({\theta }^{i},{\theta }^{-i}\right)\), each team’s quality \(\left({Q}^{i},{Q}^{-i}\right)\), and a dummy H that distinguishes the team playing at home from the one playing away. \(X\) does not include the current game result \({\Delta }_{t}\) or considerations about the time left to play in the game (\({\gamma }_{1}\left(S|X\right)={\gamma }_{2}\left(S|X\right)=...={\gamma }_{T}\left(S|X\right)\) for the same X). The underlying explanation is that the current result and time left to play in the game already influence the coaches' strategy decision (\(\theta\)), which in turn will affect the probability of scoring S points. However, equal strategy pairs affect the probabilities in the same way.

The timing of the game is the following. In the beginning of the game, teams are obviously tied (\({\Delta }_{1}=0\)) and they choose their strategy for the period \(({\theta }_{1}^{i},{\theta }_{1}^{-i})\). During the first period of the game, \({\Delta }_{2}={S}_{1}^{i} - {S}_{1}^{-i}\) occurs. At the beginning of the second period, teams choose \(({\theta }_{2}^{i},{\theta }_{2}^{-i}|{\Delta }_{2})\). Note that the strategies chosen for the second period are contingent upon which team is leading and on the point difference as well. Subsequent periods follow as period 2 did. During \(t-1,\) (\({S}_{t-1}^{i} - {S}_{t-1}^{-i})\) is revealed and \({\Delta }_{t}={S}_{t-1}^{i} - {S}_{t-1}^{-i}+ {\Delta }_{t-1}\) will summarize the score of the game at the beginning of the next period \(t\). Coaches then choose \(({\theta }_{t}^{i},{\theta }_{t}^{-i}|{\Delta }_{t})\). In the last period (T), \({(S}_{T}^{i} - {S}_{T}^{-i})\) is revealed and that marks the end of the game. The winning team collects the payoff \(x\), while the losing team gets 0. They both get \(z\) in the event of a tie. This game is solved using a sub-game perfect equilibrium concept, by the process of backward induction.Footnote 3

Last Period (T)

To ease notation, let \(Y\, C \, X\) summarize \(\left(H,{Q}^{i},{Q}^{-i}\right)\) in the list of independent variables. Also let \({W}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right)\) define the probability that team i outscores the opponent -i at the end of the game given a point difference at the beginning of the last period (\({\Delta }_{T})\). Formally,

$$\begin{array}{c}{W}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right)= \\ \sum_{\left\{{S}_{T}^{i},{S}_{T}^{-i}\right\}:{S}_{T}^{i}\pm {\Delta }_{T}>{S}_{T}^{-i}}\left[{\gamma }_{T}^{i}\left({S}_{T}^{i}|{\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}},Y\right).{\gamma }_{T}^{-i}\left({S}_{T}^{-i}|{\theta }_{T}^{-i,-{\Delta }_{T}},{\theta }_{T}^{i,{\Delta }_{T}},Y\right)\right]. \end{array}$$
(1)

Denote \({V}_{t}^{i}\) the value function of team i at the beginning of period t. The value functions depend on Y, and are also contingent upon whether team i is leading the score or not, and by how much the goal difference is (both summarized by \(\Delta\)). The value functions for the last period of the game are given by:

$$\begin{aligned}{V}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right) &=x.{W}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right)+0.{W}_{T}^{-i}\left({\theta }_{T}^{-i,{-\Delta }_{T}},{\theta }_{T}^{i,{\Delta }_{T}}|{\Delta }_{T},Y\right) \\&\quad + z.\left(1-{W}_{T}^{i}\left(.\right)-{W}_{T}^{-i}\left(.\right)\right).\end{aligned}$$
(2)

Formally, define a period T Nash Equilibrium (NE) by:

Definition 1

In a game between two teams under an environment described by Y, and for each \({\Delta }_{T}\), a strategy pair \(({\theta }_{T}^{i,\Delta },{\theta }_{T}^{-i,-\Delta })\) constitutes a period T NE if for each team i, \({V}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right)\ge {V}_{T}^{i}\left({\theta }_{T}^{i,{\Delta }_{T}{\prime}},{\theta }_{T}^{-i,-{\Delta }_{T}}|{\Delta }_{T},Y\right)\) for all \({\theta }_{T}^{i,{\Delta }_{T}{\prime}}\in \theta .\) 

Periods T-1,…,1

Having solved the NE for the last period of the game, proceed by backward induction to determine the equilibrium strategy for the previous period (and repeat the procedure all the way back to period 1). Similar to the last period problem, the NE can be found at the intersection of the reaction functions of both teams. For each strategy of the opponent, pick the strategy that maximizes the expected number of points at the end of the match. The value functions for any period \(t\ne T\) are given by:

$$\begin{aligned}{V}_{t}^{i}\left({\theta }_{t}^{i,{\Delta }_{t}},{\theta }_{t}^{-i,-{\Delta }_{t}}|{\Delta }_{t},Y\right)&= \sum\nolimits_{\left\{{S}_{t}^{i},{S}_{t}^{-i}\right\}\; \in\; P\;\times\; P}\left[{\gamma }_{t}^{i}\left({S}_{t}^{i}|{\theta }_{t}^{i,{\Delta }_{t}},{\theta }_{t}^{-i,-{\Delta }_{t}},Y\right).{\gamma }_{t}^{-i}\left({S}_{t}^{-i}|{\theta }_{t}^{-i,-{\Delta }_{t}},{\theta }_{t}^{i,{\Delta }_{t}},Y\right)\right] . \\& \quad{V}_{t+1}^{i}\left({\theta }_{t+1}^{i,{\Delta }_{t+1}},{\theta }_{t+1}^{-i,-{\Delta }_{t+1}}|{\Delta }_{t+1},Y\right)\end{aligned}$$
(3)

where \({V}_{t+1}^{i}\left({\theta }_{t+1}^{i,{\Delta }_{t+1}},{\theta }_{t+1}^{-i,-{\Delta }_{t+1}}|{\Delta }_{t+1},Y\right)\) for each team is found by using the t+1 period optimal strategy pair. Formally, the NE for period t is:

Definition 2

In circumstances summarized by Y, and for each \({\Delta }_{t}\), a strategy pair \(({\theta }_{t}^{i,\Delta },{\theta }_{t}^{-i,-\Delta })\) is a NE in period t if, for each team i, \({V}_{t}^{i}\left({\theta }_{t}^{i,{\Delta }_{t}},{\theta }_{t}^{-i,-{\Delta }_{t}}|{\Delta }_{t},Y\right)\ge {V}_{t}^{i}\left({\theta }_{t}^{i,{\Delta }_{t}{\prime}},{\theta }_{t}^{-i,-{\Delta }_{t}}|{\Delta }_{t},Y\right)\) for all \({\theta }_{t}^{i,{\Delta }_{t}{\prime}}\in \theta .\) 

There are two ways to proceed and solve the model. One, is to make assumptions regarding the behavior of the probability functions with respect to the strategies. Specifically, assume that \({\gamma }^{i}\left({S}^{i}|{\theta }^{i},{\theta }^{-i},H,{Q}^{i},{Q}^{-i}\right)\) is concave in \({\theta }^{i}\) and convex in \({\theta }^{-i}\). First order conditions could then be used to find reduced form solutions. The other method is instead to adopt a numerical and less restricted approach. Estimate the empirical probabilities \({\gamma }^{i}\) from the data directly, and use them in the model. Calibrate the model (x, z, \(\widehat{P}, T\)), define the possible strategy set \(\theta\), and for each Y (playing at home/away, different team and opponent quality measures), find the optimal \(({\theta }_{t}^{i,{\Delta }_{t}},{\theta }_{t}^{-i,{-\Delta }_{t}})\). Next, an application to the theoretical model is applied that illustrates the recursive method used to solve this model.

Applications to the National Hockey League (NHL)

To illustrate how to solve the model, a game between two teams in the NHL is considered. Choose teams that are evenly matched in their quality, making the home/away factor the discriminating variable in Y.Footnote 4 As per current NHL rules, there are 3 periods in the game with the winning team collecting 2 points, and 0 for the one that loses the game. If tied at the end of the third period, both teams play an extra fourth period (overtime) with the same rewards for winning and losing the game. If still tied at the end of overtime, there is a penalty shootout game where again 2 points are awarded to the winning team, and 1 to the losing opponent. It is assumed that each team collects 1.5 points in the shootout, the average of the empirical probabilities of 50% chance of winning (2 points) and 50% of losing the game (1 point). To capture this reward system and duration of the NHL game, let T = 4, x = 2 and z = 1.5. Set the strategy set of possible coaching decisions during each of the periods in the game to be \(\theta =\{0.2, 0.5, 0.8\}\). Consider that each team can score 1 or 0 goals in any single period of the game (\(\widehat{P}=1\)). In this game (and any game in the NHL), teams are tied at the beginning of the first and fourth (overtime) periods, but they might be ahead, tied, or losing the game at the start of the second and third period. The exercise is then to find the optimal strategies for the fourth period \(({\theta }_{4}^{i},{\theta }_{4}^{-i})\), the third period conditional on the result at the end of the second \(({\theta }_{3}^{i,\Delta },{\theta }_{3}^{-i,-\Delta })\) for all \(\Delta =\{-2, -1, 0, 1, 2\}\), and also to find the optimal strategies for the second period conditional on the result at the end of the first \(({\theta }_{2}^{i,\Delta }, {\theta }_{2}^{-i,-\Delta })\) for all \(\Delta =\{-1, 0, 1\}\), and finally the optimal strategies for the first period \(({\theta }_{1}^{i}, {\theta }_{1}^{-i})\). In total, 8 optimal strategy pairs are sought.

The game is solved by backward induction. Starting with the overtime period, use Eq. (2) for the home team, replace all possible \({\theta }^{i}\) for each \({\theta }^{-i}\), and choose the one yielding the maximum expected value for the home team (the probability values \({W}^{i}\) and \({W}^{-i}\) that are necessary to solve this equation are found by replacing in Eq. (1) each of the strategy pairs being evaluated). That results in a best-response function of the home team to each of the opponent’s possible \({\theta }^{-i}\). The same is done for the away team, but with reversed roles in Eqs. (1) and (2). The intersection of both reaction functions results in the NE for the last period. Repeat the procedure for periods 3 and 2, and for each \(\Delta\) at the beginning of the corresponding period, to find each solution pair contingent on each possible game scenario. For each of the cases, evaluate value functions in Eq. (2) using the optimal strategy pair for the following period (that was just found in the previous iterative step), and replace them in Eq. (3) to find the best response functions for each team in that period. Once again, the NE will be found from the intersection of both reaction functions. The optimal solution for period 1, also follows the same steps with the nuance that there is only one game scenario (\(\Delta =0\)) since teams are always tied at kickoff. Table 1 shows the per-period probability of scoring a goal for either team. Figure 1 illustrates the best-response functions for both teams in different scenarios of the game.

Table 1 Per-period scoring probabilities in a National Hockey League game
Full size table
Fig. 1
figure 1

Teams’ best-response functions (1st, 2nd, 3rd, and 4th periods)

Full size image

The 8 NE solution pairs that solve this game are presented in Table 2 (fourth column in panel B). The optimal solutions to this game provide a clear indication of whether coaches should adopt defensive or offensive strategies during a game in the NHL, and how these depend on the current period and score of the game. It can be concluded that both teams should choose to attack when behind in the score, and defend if ahead (independently if it is the start of the second or the third period of the game). When tied, teams should play defensively with the exception of the strongest (home) team at the start of the match.

Table 2 Nash Equilibrium solutions to the National Hockey League game
Full size table

A second very interesting application of the model, is to see how these optimal model predictions would change with a different point system or a change in the rules of the sport. One can study how team strategic behavior is affected when there is a change in the incentives. This analysis can guide policy for those in charge of the NHL, and help to male changes that affect the sport in a positive way. Fans enjoy offense and watching goals, and this exercise can yield clear predictions on whether that can be achieved in a different setting.

To that end, four alternative specifications are considered. The first test is how optimal decisions would change when removing the overtime period and replacing it with 1 point awarded to each team. This is the conventional method used in other sports, such as soccer. Specifications 2 and 3 also assume removal of the fourth period in the game and test what would happen if the incentives to win the game increased disproportionately to those in the event of a tie (to three and four points, respectively). The last specification considers keeping the overtime period, but removing the one-point reward that teams losing the penalty shootout currently receive. The point system under each of the specifications is summarized in Table 2 (panel A), and the resulting NE strategy pairs can be found in the last four columns on Table 2 (panel B).

In all scenarios considered, teams should still attack the most when behind in the score, and defend when ahead. However, there are differences in teams’ strategic behavior for the cases when teams are tied at the beginning of the period. When removing the overtime period, the home team now also chooses to attack the most at the beginning of the second and third periods of the game, while in the current system the home team was choosing to defend. Further increasing the rewards of a win (3 points), also leads the away team to play more offensively when tied at the start of the (what is now the last) third period. If the rewards of a victory are increased even further (to 4 points), then the away team will choose to play more offensively if tied in the beginning of the second period as well. Finally, not rewarding a point to the losing team at the shootout, makes the home team choose the most offensive style of play when tied, independent of the match period. In conclusion, all the specifications considered could potentially lead to more attacking behavior in the NHL.

Conclusion

This article presented a model that investigates the strategic choice between offense and defense. The model is purposeful in that it evaluates whether the observed coaches’ strategic decisions are optimal. In any of the major sports, coaches are very well paid, particularly those in the top teams. Model predictions facilitate investigation of whether the coaches’ decision to play defensively or offensively is or is not rationally justified.Footnote 5 The fact that the model has rich dynamics permits evaluation of different moments of the game, and how those decisions can/should change with the current score and time left to play. Consideration of team and game characteristics (playing at home or away, and each team’s quality), makes the exercise realistic in that different game scenarios can be contemplated.

The model’s potential was explored using the NHL. Under current rules and the existing point system in the league, optimal coaching strategies are found for different scenarios in a game. It is shown that teams should choose to play defensively when ahead in the score, and attack when behind. In the event the game is tied at the beginning of the second, third, or fourth (overtime) periods, both teams should play defensively, while at the start of the game (tied game, first period), the home team should attack and the away team should defend. Secondly, the impact of alternative rule and point systems in the sport was tested. The results indicate that removing the overtime period, disproportionally increasing the rewards for a win, or removing the point currently awarded to the team that loses the shootout at the end of overtime, would all lead to the adoption of more offensive strategies during the game. That is an outcome definitely aligned with fan interest and team revenue.

One interesting next step in this research would be to use the model to find the optimal rule (point system) in a specific sport. For instance, using the NHL example presented in the paper, an appropriate welfare function can be used to capture fans’ preferences (balanced between more goals and competitiveness in the game). Then, from a planner’s perspective, the impact of different x, z point combinations on teams’ behavior and consequently welfare, could be studied and the optimal rule found. A second possible extension of this work would be to apply the model to situations where there are known, finite periods of interaction between the players/teams. The recursive solution method used to solve the model also relies on (T) being known. It would be interesting to consider a setting where there is an unknown/infinite number of moments where the players or teams are making strategic decisions.