Abstract
Recently, studies with different methods (computable general equilibrium models, dynamic stochastic general equilibrium models, structural gravity equations) evaluated the European Union’s Single Market. The problem with all these studies is that they use complex models with datasets that are not always replicable. This paper demonstrates that even a simple model of the European Union can capture the most important effects of European economic integration: the European Union’s Single Market, the introduction of the Euro, and the following European Union enlargements. A simple European Union model, built with the publicly available program, EViews, serves this purpose. The dataset is also freely available from the European Commission. This makes the model results replicable. Evaluation of Austrian membership in the European Union is in the foreground of the analysis with the simple European Union model, followed by the next steps of integration, such as the introduction of the Euro and the big European Union enlargements. However, this prototype model is also able to estimate the integration effects of other European Union member states.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In the context of the discussion about Brexit and the 25th anniversary of the creation of the Single Market (SM) of the European Union (EU), studies examined the importance of the SM for trade, growth, and welfare of the EU member states. Except for one study (Andersen et al., 2019), all concluded that EU’s SM increased trade, welfare, and growth. They use the most advanced and complex methods, either in the form of computable general equilibrium (CGE) models, dynamic stochastic general equilibrium (DSGE) models or through the application of structured gravitational equations. As valuable as these studies are, they are not very transparent and replicable.
The purpose of this paper is to develop a simple EU model that uses easily available data, and is replicable in EViews. Firstly, a short literature overview shows the most recent attempts to evaluate the EU’s SM. Then a simple 10-equation EU model is developed, covering the most essential EU integration effects: (a) trade effects, resulting from participating in the EU’s SM, the introduction of the Euro and the grand EU enlargement, (b), the competition effects, (c) the impact of the net budget position vis à vis the EU budget, and lastly (d) the resulting growth effect of European integration. The study concludes with the application of this prototype EU model for Austria and a selected number of EU member states (MS): founding members and new MS which joined the EU later and which are Euro or non-Euro countries.
Literature Overview
Many studies evaluated ex ante the deepening steps of European integration, starting with the EU’s Single Market in 1993, creation of the Economic and Monetary Union (EMU) in 1999 with the introduction of the Euro in 2002, and possible effects of the grand enlargement of the EU, starting in 2004. Fewer studies cared about the outcome of these fundamental integration steps. This review describes only briefly the most important recent studies which primarily deal with the impact of the EU’s Single Market.Footnote 1 Similar to the ex-ante studies, those done ex post also applied a variety of methods: model-based studies and econometric analyses. Whereas the model-based ex post evaluations of the EU’s Single Market found that the growth effects for trade and gross domestic product (GDP) are positive, econometric studies (e.g., Andersen et al., 2019) found no significant effect of European integration on economic growth.
Econometric Approach
London Economics (2017) used an econometric model to measure the impact of the EU’s Single Market. It provides an estimate by relating five variables of interest to the summary indicator of Single Market integration, constructed using 17 different indicators. The five variables of interest are: (1) GDP (measured by GDP per capita), (2) household consumption (measured by household consumption per capita), (3) employment (measured by the employment rate), (4) productivity (measured by total factor productivity growth), and (5) investment (measured by gross fixed capital formation). London Economics (2017) estimated its model for all EU Member states for the period 1995 to 2015 (except for Croatia, Malta, and Luxembourg). Overall, the results suggest that Single Market integration since the completion of the Single Market Plan (SMP) had a direct, positive, and statistically significant impact on the growth of per capita GDP, per capita consumption and employment, and total factor productivity. While the Single Market had no direct impact on investment, the growth of Single Market integration still had an indirect effect. GDP increased, in turn stimulating investment. The resulting estimates show that EU GDP per capita is 1.0% higher than it would have been without an increase in integration since 1995. Moreover, there are almost 1.9 million additional jobs. If the beginning of the Single Market had started already in 1990 (i.e., pre-Single Market), then the impact of the Single Market would have been even greater. GDP per capita would then have been 1.7% higher.
The longer a country is a member of EU’s Single Market, the higher are the growth effects. As a result (London Economics, 2017, p. 35, 37), the impact of Single Market integration on GDP per capita in 2015 since the completion of the Single Market (in 1993) or since the accession of new member states was highest in Austria (+ 1,7%) and lowest in Greece (-0,3%). The incumbent Germany increased its level of GDP per capita by 1,6%. The Czech Republic (+ 0,8%) had the best performance of the new member states after the grand EU enlargement in 2004. The countries which only entered the EU in 2007, like Bulgaria (+ 0.02%) and Romania (+ 0.1%), could not yet profit from EU accession.
New Quantitative Trade Model
Felbermayr et al. (2018) conducted simulation experiments that shed light on the economic benefits arising from various steps of European integration. Hence, they simulated the economic consequences of “undoing Europe”. For this purpose, they used the ifo trade model, a CGE model, termed in the literature as a new quantitative trade model (NQTM). The model features 43 countries and 50 goods and services sectors with data from the World Input–Output Database (WIOD) over the period 2000–2014. “Undoing Europe” was simulated by looking at seven different counterfactual scenarios: (1) the collapse of the European Customs Union (tariff-free trade replaced by most favored nation (MFN) tariffs), (2) dismantling the European SM, (3) dissolution of the Eurozone, (4) breakup of the Schengen Agreement, (5) undoing all regional trade agreements (RTAs) with third countries, (6) complete collapse of all European integration steps, (7) complete EU collapse including the termination of fiscal transfers.
Overall, the largest losses of income per capita in the base year 2014 would result from the dissolution of the SM which is at the heart of EU integration (Felbermayr et al., 2018, p. 24). The complete collapse of all EU integration steps would have significant welfare losses. Income per capita of the EU28 would shrink by 10.2%, but heterogeneity would exist across countries. Luxembourg (-23.3%) would suffer the most, followed by Malta (-17.8%) and the new EU Member states, which acceded the EU in 2004 like Hungary (-14.2%) and the others in the range of around -11%. From the three EU newcomers in 1995, Austria (-6.2%) would suffer from the end of the EU more than Finland (-3.8%) and Sweden (-4.2%). Germany (-5.2%) would lose less than the EU on average.
Dynamic Stochastic General Equilibrium Model
In’t Veld (2019) evaluated the macroeconomic benefits of the EU’s SM by applying the European Commission’s QUEST DSGE model. The model used in this simulation exercise is a multi-country version of the QUEST model. QUEST is a structural macroeconomic model, derived from micro-principals of dynamic intertemporal optimization. It distinguishes between a tradable and non-tradable sector, both importing intermediate goods, and models bilateral trade flows of traded goods. In’t Veld (2019) only reported long-run effects. In’t Veld (2019) simulated two counterfactual scenarios, which should capture the non-SM effects:
The first scenario examined the effects of trade barriers. In the SM simulation, the author added MFN tariffs and non-tariff barriers (NTB), although at the start of the SM the EU had already eliminated the MFN tariffs in intra-EU trade. The increase in trade costs of around 13% reduced intra-EU trade (intra-EU imports) by 20–30%, while total imports fell by about 20%. The decrease in imports was larger than that in exports. The increase in trade costs not only affected trade flows but also had a direct impact on domestic demand and hence on GDP (in the long run -6.6% for EU28). In the QUEST model, lower GDP was mostly a productivity effect, which is the result of lower investment.
The second scenario examined the effects of lower competition. Greater trade openness of the SM increased competition and lowered prices, and the re-establishment of trade barriers (as in first scenario) is likely to reduce competitive pressures. If one assumes that the undoing of the SM would lead to an increase of mark-ups in manufacturing by 26% (no effect in the services sectors), real GDP of EU28 would be lower by 2.1%.
Summing up the results of these two scenarios gives the total long-run effects of the counterfactual non-SM (In’t Veld, 2019, p. 814). Real GDP in EU28 would be lower by 8.7%. The effects differ from country to country. The biggest losses would occur in Luxembourg (-20.5%), followed by Slovakia (-19.3%), the Czech Republic (-18.5%), Belgium (-18%) and Hungary (-16.5%). Austria (-11.8%) would suffer more than Finland and Sweden (both -7.7%). The large incumbent member states, like France (-7.1%), Germany (-7.9%) and Italy (-6.8%), would lose less than the EU on average.
In’t Veld’s (2019) estimates are comparable to those of Mayer et al. (2019) and Felbermayr et al. (2018), who used gravity trade models to estimate the trade and welfare effects from European integration. Mayer et al. (2019) reported large trade effects and welfare losses for the EU of up to 5½%. Felbermayr et al. (2018) reported income per capita effects for their SM disintegration scenario that are on average around 6.4% for the EU28. While the country ranking in these two studies showed strong similarities to those of In’t Veld (2019), their welfare or income per capita effects were lower than the GDP effects of In’t Veld (2019). Part of this difference is due to the competition effects included in the results of In’t Veld (2019), but not included in the two other studies.
Computable General Equilibrium Models
Mion and Ponattu (2019) applied a CGE trade model to study the economic benefits of the EU’s SM for countries and regions across Europe. The model captures the impact of the trade boosting effects of the SM on productivity, markups, product variety, welfare, and the distribution of population across European countries and regions. The CGE model includes ingredients such as costly trade, love of variety, heterogeneous firms, labor mobility as well as endogenous markups and productivity. The authors used data on trade in goods (services) from the COMTRADE (ITS) database provided by the United Nations (Eurostat) for the period 2010–2016. The simulations were conducted for EU countries and European regions (283 NUTS2 regions), and for 14 other countries of the Organisation for Economic Co-operation and Development (OECD) and BRIC (Brazil, Russia, India, and China) trading partners.
The long-run country results (Mion & Ponattu, 2019, p. 12) showed that the SM provides higher welfare, higher productivity, and lower markups to all its members while at the same time countries outside the SM are actually (slightly) worse off because of the existence of the common market. The country results showed considerable heterogeneity. Overall, the long-run (in the period 2010–2016) welfare (income per capita) gains due to EU’s SM, were highest in Belgium (+ 4.4%) and Luxembourg (+ 4.3%), followed by the Czech Republic (+ 4.0%), Austria and Slovenia (each + 3.9%). Finland (+ 2.5%) and Sweden (+ 2.8%) could profit less from EU accession. The large incumbent EU member states, like France (+ 3.1%), Italy (+ 2.8%) and Germany (+ 2.7%) ranked in the middle of welfare benefits of the EU.
Our own simulations of an “Undoing the EU” scenario are comparable to those of In’t Veld (2019). The simulations with a CGE model, were executed with the CGEBox of Britz (2019) and Britz and Van der Mensbrugghe (2018). Version 10 of the Global Trade Analysis Project (GTAP) database (2014) is based on data from 2014. The model consists of 20 sectors and 20 countries. In contrast to In’t Veld (2019), this model simulates the “Undoing the EU” with only one scenario, namely the re-introduction of non-tariff measures (NTMs) between the EU member states. The elimination of NTMs constitutes the core of EU’s SM, starting in 1993. The problem with the implementation of NTMs is that they are only rough estimates. The most recently estimated NTMs stem from Arriola et al. (2020). The re-introduction of NTMs leads to a reduction in trade and economic growth. Intra-EU trade would shrink by 18% (Armington version) to 27% (Melitz version).Footnote 2 This translates into a medium-run reduction of real GDP in EU28 by 0.5% (Armington) to 2.8% (Melitz). Ireland would be the big loser: GDP loss of 1.2% to 8%. Austria would lose disproportionally (-0.8% to -4.9%); Finland (-0.6% to -3.3%) and Sweden (-0.7% to -3.4%). The GDP losses are lower in these simulations than those of In’t Veld (2019) mainly because this model does not re-introduce MFN tariffs. Due to the completion of the EU’s customs union in the 1960s, MFN tariffs no longer exist in the case of intra-EU trade.
An Outlier
Andersen et al. (2019) evaluated the contribution of EU membership to economic growth. Asking the question whether it was worthwhile joining the EU to trigger prosperity, they econometrically regressed economic growth (annual growth rate of real GDP per capita) to a dummy variable for EU membership (taking the value of 1) with different databases (OECD, Penn World Tables (PWT), World Development Indicators (WDI)) for periods since 1960 with and without the crises years (financial crisis 2009, Euro crisis 2010) and various econometric panel approaches (with and without considering convergences or catch-up effects). Lastly, the authors (Andersen et al. (2019), p. 233) concluded that “this paper has been unable to reject the null hypothesis that ‘EU membership has zero impact on economic growth’”. In evaluating 25 years of the EU’s SM, Breuss (2020b, p. 329) came to a contrary conclusion. Using smart EU indicators and regressing these to real GDP per capita resulted in a significant impact of EU integration on EU’s economic growth. Accordingly, EU28 could increase real GDP per capita since 1993 by 0.5% per year, in the whole period of European integration (1958–2019) only by 0.3% per year.
In its own way the Anderson et al. study underlined the so-called EU integration puzzle. This means that it is difficult to explain why the EU (despite a steady deepening of integration since World War II) could not achieve higher economic growth than the United States (U.S.). This contradicts all predictions of the various integration theories and most ex-ante studies evaluating the growth-enhancing effect of EU integration, especially those of EU’s SM.
The Model
One of the major features of such integration studies is that they need overly complex and often large trade or DSGE models or highly sophisticated econometric techniques. Furthermore, they use various kinds of databases, not always available for all researchers. The most significant caveat of these studies is that they are not easily replicable.
The following simple 10-equation EU integration model aims at filling the gap of these caveats:Footnote 3
-
1.
It features the major impact factors of EU integration on trade and GDP growth: trade effects of EU’s SM, EMU/Euro, and EU enlargement since 2004, net position vis à vis the EU budget (neglected by most previous studies), more competition in EU’s SM, and growth effects on GDP via an increase in total factor productivity (TFP).
-
2.
It encompasses these integration effects in a simple macroeconomic model in EViews with ten equations.
-
3.
This study only uses two easily accessible databases: the annual macroeconomic (AMECO) database (European Commission, 2022a) and the budget data of the European Commission (2022b).
-
4.
This simple prototype model of EU integration, estimated in EViews, evaluates Austria’s EU accession.Footnote 4 However, his prototype model is easily reproducible and applicable to other EU Member states, be they incumbents (like Germany) or newcomers in the 1995 enlargement (Austria, Finland, and Sweden) and those during the last grand EU enlargement in 2004 (like Hungary), and for EU member states with and without the Euro.
The results of this study are replicable because the applied model (EViews) is transparent, and the databases used are freely and easily accessible.
In the spirit of Luhmann (1997), this is an attempt to reduce the complexity of the European integration process. European integration is a multidimensional and multidisciplinary project. It has political, legal, and economic dimensions. When trying to evaluate the economic effects of European integration, one simply hides the other dimensions. Nevertheless, even the economic dimension is complex enough. Therefore, this study isolates the major features of possible economic impacts of being a member of the EU. Four effects are essential to evaluate the impact of EU integration.
One of the major features are the trade effects of the SM. The latter should also have contributed to more competition. Because the EU is composed very heterogeneously, EU member states are either net recipients (poor countries) or net payers to the EU budget (rich countries). Finally, according to integration theory, EU membership should also lead to prosperity, measured by the growth of GDP or GDP per capita.
Trade Effects
The first and essential impacts of European economic integration are the trade creation effects. This started in 1968 with the formation of the EU Customs Union, eliminating bilateral tariffs between EU member states. The creation of the EU’s SM in 1993 reinforced trade creation by eliminating NTMs in intra-EU trade. All previously reviewed studies that evaluated the economic impact of the EU’s SM concluded that intra-EU trade increased. However, this was done by applying a vast variety of methods. Either they re-introduced MFN tariffs and NTMs in their models and in CGE simulations (Felbermayr et al., 2018; Mion & Ponattu, 2019; In’t Veld, 2019) or EU membership was captured with a dummy variable in structural gravity trade models (Oberhofer, 2019).
In the following, the trade impact of the EU’s SM is in the foreground. Therefore, tariffs do not play a role, because they did not exist before 1993. To detect the possible trade effects, the major factor of trade costs is NTMs. Ideally, one would like to know the exact size of the NTMs which could then be eliminated, not all at once but gradually, starting with the inception of the SM. Unfortunately, the NTMs are very heterogenous between EU member states and differ from sector to sector. Therefore, exact figures are not available. There are various attempts to estimate NTMs. However, they vary from study to study. Also, the authors reviewed herein used various sources of estimations of NTMs. Therefore, a comparison is not possible.
To get around these problems, let the data speak for itself. This model uses dummy variables to capture the trade costs which gradually decline once a country participates in EU’s SM. Furthermore, this model measures the impact of SM participation in intra-EU trade. The data for intra-EU trade (exports and imports of an EU member state going to or coming from the EU) are available from the AMECO database (European Commission, 2022a).
Intra-EU exports of goods (free on board (FOB); billion EUR in current prices) of EU member state (i) in time (t)
depend (positively) on the EU dummies. The three dummies (SM, €, EL) reflect the three fundamental regime changes of the EU since the early 1990s. \(SM\) stands for the creation of EU’s Single Market in 1993. For EU member states that joined the EU later, the SM dummy starts in the year of EU accession. For incumbent member states like Germany, the SM dummy takes the value of 1 from 1993 to 2022. € is the dummy for the creation of EMU in 1999 and introduction of the euro in 2002. The € dummy takes the value of 1 from 1999 to 2022. The last big regime changes and the concurrent extension of the EU’s SM was the grand EU enlargement, starting in 2004. The EL dummy gets the value of 1 from 2004 to 2022.
Intra-EU imports of goods (FOB; billion EUR in current prices) of EU member state (i), in time (t), \({M}_{EUi}\), are modeled similarly to the intra-EU exports:
All equations of this EU integration model (except those for the net budget position) were estimated with EViews in logarithms. All other equations included one lagged endogenous variable to capture all factors other than EU integration (Online Supplemental Appendix). This gives the model a dynamic feature.
An essential point in correctly capturing the EU effect via the EU dummy is the timing. The integration process of the completion of the SM, creation of the EMU with the introduction of the Euro and enlargement of the EU’s SM by the grand enlargement of the EU from 15 to 28 member states took time. Therefore, the three dummies for the three regime changes of the EU integration were coded as ones over the whole period.
Total exports of EU member state (i), in time (t),
depend on the estimated intra-EU exports. The plus sign ( +) indicates the expected direction of the influence of the explanatory variable.
Similarly, the total imports of EU member state (i) in time (t) are
They depend on the estimated intra-EU imports. Of course, in both equations the intra-EU trade has a positive impact on total trade. From total trade, one can calculate the trade balance, \({TB}_{it}= {X}_{totit}- {M}_{totit}\).
Competition Effects
The creation of the EU’s SM should have had an impact on competition. Greater trade openness (increased intra-EU trade) increased competition and lowered prices. Firms lost the market power to markup their prices over marginal costs, which had a positive impact on output. According to the study by Badinger (2007) markups went up in most service industries of the EU’s SM since the early 1990s, confirming the weak state of the SM for services, and provoked an additional liberalization program of services in the EU.Footnote 5 However, in the manufacturing sectors, markups declined on average by 26%. In’t Veld (2019, p. 812) used this figure in his counterfactual simulations of the impact of the non-SM. There are recent studies by the European Commission (Cai et al., 2020, p. 12), demonstrating that EU’s strict competition policy had a considerable impact on GDP. The authors used the European Commission’s QUEST III model to evaluate the macroeconomic impact of competition policy enforcement. Accordingly, prices (GDP deflator) decreased by 0.2 percentage points (ppts) after five years and real GDP increased by 0.3 ppts (see also an overview of similar studies by Ilzkovitz & Dierx, 2021).
With a political economy model of market regulation, Gutiérrez and Philippon (2018) showed that countries in a SM (like those of the EU) willingly promote a supranational regulator that enforces free markets beyond the preferences of any individual country. European institutions (the European Commission) are more independent and enforce competition more strongly than any individual country ever did. Countries with ex-ante weaker institutions benefit more from the delegation of competition policy to the EU level. Over the last two decades, U.S. markets have gradually become less competitive. Today, European markets are more competitive than those in the U.S., which invented modern antitrust in the late nineteenth and early twentieth century. By 1950, it was clear to most observers that American markets were more competitive that European ones. The creation of the EU’s SM with its fierce competition policy was the turning point (European Commission, 2022c).
In this simple integration model, EU dummy variables for being a member of EU’s SM capture the competition or markup effects. Accordingly, entering the EU’s SM leads to a flattening of consumer price inflation. The Harmonized Index of Consumer Prices (HICP) of EU member state (i) in time (t),
depends (negatively) only on the EU dummy representing the EU’s SM \(.\) In the simulations, they have the suffix “MUP” for markup. The GDP deflator,\({P}_{GDPit}\), depends on consumer prices:
Net Budget Position
The EU is a solidarity community. The Treaty of the EU (TEU) states in Article 3 that “It shall promote economic, social and territorial cohesion, and solidarity among Member states.”. To fulfil this objective a redistribution mechanism has been established in the Treaty on the Functioning of the European Union (TFEU) under Title XVII: Economic, Social and Territorial Cohesion. Via specific financial instruments, the rich EU member states finance the poor ones.
Practically, all studies reviewed herein neglect the budgetary aspect of EU integration. In fact, the impact of the net position of the EU member states is considerable: negative in the incumbent rich countries and positive in the new member states in Eastern Europe.
Data from the European Commission (2022b) on the net position of its member states (operating budgetary balances) show that, e.g., Germany is the largest net payer into the EU budget (14.3 bn EUR in 2019). Over the period 1992–2018, Germany’s net contribution to the EU budget amounted to 0.4% of its gross net income (GNI). On the other side, Poland was the biggest net receiver from the EU budget (12.0 bn EUR in 2019), followed by Hungary (5.1 bn EUR). In the period 2004–2018, Hungary received regional transfer income from the EU budget amounting to 3% of its GNI (Poland 2% of GNI).
The following definition (identity) serves to evaluate the effect of the net budgetary position vis à vis the EU budget on real GDP:
Real GDP (\({GDP}_{it}\)) is corrected by the real net position vis à vis the EU budget (\({NETEU}_{it}/{P}_{GDPit}\)) and results in a net budget position adjusted real GDP (\({GDP}_{neteuit}\)).
Growth Effects
Finally, the trade effects translate into growth effects. Most theories on economic integration (Baldwin & Venables, 1995; Kohler, 2004) postulate a growth effect of integration, primarily via more investment, stimulating productivity (In’t Veld, 2019, p. 811).
In this reduced form model, the assumption is that more openness (increase of exports plus imports) stimulates productivity. The latter is the major driver for GDP growth.
Total factor productivity (\({TFP}_{it}\)) of the EU member states (i) in time (t) increases when the trade volume (trade openness) increases. The latter is a consequence of deeper integration into the EU’s SM:
TFP positively stimulates real GDP (\({GDP}_{it}\)) of the EU member states (i) in time (t). However, inflation measured by the GDP deflator exerts a negative influence on real GDP:
Finally, welfare measured by GDP per capita (\({GDP}_{pcit}\)), nominal in 1000 PPS) is determined by the development real GDP:
The signs ( ±) indicate the expected direction of influence of the explanatory variables. This 10-equation model captures two major ingredients of European integration. The growth or GDP effects are endogenous via the trade and competition effects. One obtains the overall impact of European integration on Austria’s real GDP by adding the net position vis à vis the EU budget. The estimated equations for the Austrian EU integration model are in the Online Supplemental Appendix.
Integration Scenarios and Results
The simple Austrian EU integration model permits simulation of the following integration scenarios: Trade, competition, EU budget and growth. The trade effects of participation in the EU’s SM (in the case of the EU accession in 1995) is captured in Eqs. (1) and (2) with the three dummy variables: SM (EU95 for EU accession in 1995), € (EU99 for participation in the EMU/Euro in 1999) and EL (EU04 for the grand EU enlargement, starting in 2004). As mentioned earlier, the three EU dummy variables take a value of one over the whole period of integration (1995 to 2022). The counterfactual scenario assumes that the respective EU dummies are equal to zero. The trade integration effects are the results of the comparison of the baseline (actual) development of intra-EU trade (competition, EU budget) with the counterfactual simulated trade development.
Competition: The SM dummy variable for the EU’s SM (EU95MUP for mark-up) in the consumer price Eq. (5) captures the competition effect of participation in the EU’s SM. The procedure for the respective counterfactual scenario is the same as for the trade effects.
EU budget: Eq. (7) defines the influence of the net budget position vis a vis the EU budget impact on real GDP. \({NETEU}_{it}\) contains the actual net payments of Austria to the EU budget. In the counterfactual scenario, this variable is simply set to zero.
Growth: Including the trade effects into the TFP Eq. (8) and the competition effects into the GDP Eq. (9) delivers the growth effects of EU integration. To derive the total GDP effects, the model also adds net position vis a vis the EU budget. The growth effects of EU integration, trade (participation in EU’s SM and in EMU/Euro), competition, and net budget effects, are then the result of the comparison of the baseline scenario (actual development of real GDP) with the simulated counterfactual scenarios (if no EU accession had taken place).
Results for Austria
In general, the results of the present simple EU integration model are comparable but a bit lower than those of previous estimates of the integration effects of Austria's EU membership. This may be the outcome of fewer interdependencies than in more complex models. Overall, Austria’s EU membership (simulated over the period 1995–2022) resulted in 0.47% additional annual growth of real GDP (Table 1).Footnote 6 The nominal total Austrian exports increased between 1995 and 2022 by 166% (or by 6% per year). Total imports improved by 143% (or 5% per year; Table 2). The competition effect of participating in EU’s SM did not add up much to the overall result (Table 1). As a net payer into the EU budget, the transfer system of the EU reduced Austria’s GDP.
The greatest annual growth effect of joining the EU’s SM comes from the trade effects (+ 0.44%; Table 1). However, Austria profited as a member of the European Free Trade Association (EFTA) since 1973 and of the European Economic Area (EEA) since 1994 before the creation of the SM. The Free Trade Agreements between the EC and the EFTA in 1973 (which led to a free trade area for industrial goods in Europe since 1977) and the EEA membership in 1994 already led to a free trade area in Europe. The accession to the EU and associated entry into the SM in 1995 did not immediately contribute much to the increase in intra-EU trade. The reason is that the SM led only to a gradual elimination of the remaining NTMs. Nevertheless, the model estimates a cumulative increase of intra-EU exports by 39% and of intra-EU imports of 31%, which resulted in a positive trade balance effect because the total exports and imports also developed comparably (Table 1). The trade effects of introducing the Euro and that of the grand EU enlargement in 2004 were even higher than joining the EU in 1995 (Table 1). Summarizing the three integration steps, total intra-EU exports increased by 144%, intra-EU imports by 118%, resulting in a cumulative improvement of the trade balance of 2.7% of GDP since 1995.
Participation in the EU’s SM should have led to pressure on monopoly power and an increase in competition. In fact, the model simulations show that consumer prices decreased by 1.2% per year since 1995 (Table 1).
Austria’s EU membership led to a cumulative increase of real GDP (at 2015 prices) since 1995 by 47 bn EUR (or 2 bn per year) or over 13 percentage points (Table 1 and Fig. 1). Austria’s welfare measured by GDP per capita (in PPS) improved cumulatively by 5,100.

Source: Own simulations with the Austrian EU integration model (Online Supplemental Appendix), using data from AMECO database (European Commission, 2022a) and European Commission (2022b). Note: Cumulative changes are deviations from the baseline with no EU membership
Austria in EU: 1995–2022 – Total integration level effects.
The aim was to keep the present model slim. Nevertheless, it would be easy to add equations, e.g., representing the labor market, to the ten equations in the simple EU model. This is done by adding a simple equation for total employment (EE = f(GDP)) and for the unemployment rate (Okun’s law: \(\Delta\) U = f(GDP%). As a result, Austria’s EU membership since 1995 should have added 321,000 persons to total employment (or an annual increase of 0.26%). The unemployment rate should have been reduced cumulatively since 1995 by 0.1 ppts.
Level Versus Growth-Rate Effects
The studies mentioned in the literature review did not address the important question of whether EU integration leads only to a level or also to a growth rate effect of GDP. Representatives of the endogenous growth theory (e.g., Romer, 1990) postulated that economic integration via economies of scale lead to a permanent steady-state growth effect of GDP. Accordingly, larger countries grow faster than smaller ones. Doubling the size of an economy (or doubling the size of the domestic market or those of the EU’s SM) would, therefore, double the steady-state growth rate of GDP. Jones (1995) and others sharply criticized this approach. In an evaluation of 25 years of the EU SM using a growth equation, Breuss (2020b) rejected the idea of a permanent growth rate effect through EU integration.
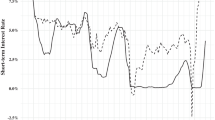
Figure 1 represents the cumulative changes of real GDP or level effects of European integration. The changes are deviations from the baseline with no EU membership. These impulse-response representations are the result of the simulation of the previously-described economic integration effects with the simple EU model.
Level Effects
Figure 1 shows the level effects of Austria’s EU integration, overall and for the separate integration steps. After each integration step (EU accession in 1995, EMU participation in 1999 and EU enlargement in 2004) the EU dummy variables lead to a jump in the levels of real GDP which then flatten out in the absence of further integration steps. Due to the specification of the EU dummies, the overall picture of the cumulative increase of real GDP resembles a logistic function.
Growth-Rate Effects
Figure 2 depicts the GDP growth rate effects of Austria’s EU integration. As can be seen, they are only short-lived. Each of the three major new integration steps (EU accession, EMU/Euro, and EU enlargement) led only to a temporary increase of the growth rate of real GDP. Also, the sum of the growth rate performance of all integration steps reflects this pattern. After the initial integration impact, the growth rate declines until another integration impulse might arise. Hence, the simple EU model does not confirm Romer’s (1990) postulation of a steady-state or permanent growth-rate effect of economic integration.
Austria in EU: 1995-2022 – Total integration growth rate effects. Source: Own simulations with the Austrian EU integration model (Online Supplemental Appendix), using data from AMECO database (European Commission, 2022a) and European Commission (2022b). Note: The annual growth rates are deviations from the baseline with no EU membership
Results for Selected EU Member States
Now, the simple 10-equation-prototype EU integration model for Austria (Online Supplemental Appendix) is applied to a selected number of EU member states with differing histories of EU membership. This exercise is done for three EU founding member states (France, Germany, and Italy) with the Euro, three countries of the 1995 EU enlargement (Austria and Finland with the Euro and the non-Euro country Sweden), three countries of the 2004 enlargement (the non-Euro countries Hungary and Poland, and Slovakia with the Euro), and Bulgaria without the Euro, joining the EU in 2007.
The studies reviewed earlier are mostly static as far as they do not differentiate between the timing of EU accession. They even ignore the fact that not all EU member states have introduced the Euro. The simple EU model can differentiate in these respects between the EU MS. Figure 3 illustrates the timing of the selected EU member states concerning their EU membership, again shown as level effects. Whereas the three founding members (France, Germany and Italy) entered the EU’s SM right at the start in 1993, their cumulative GDP integration effects also began to materialize after that date. The next new EU member states (Austria, Finland, and Sweden) joined the EU and hence the SM in 1995 and the integration effects began to take off. Accordingly, Finland and Sweden increased cumulatively their GDPs more than Austria. The new member states of the next EU enlargements in 2004 (Hungary, Poland, and Slovakia) and 2007 (Bulgaria), therefore, had less time to profit from EU integration.
The timing of the total integration level effects of selected EU MS. Source: Own simulations with separately estimated EU models for each of the above EU MS according to the Austrian EU integration model (Online Supplemental Appendix) using data from AMECO database (European Commission, 2022a) and European Commission (2022b). Note: The cumulative changes are deviations from the baseline with no EU membership
The results of the simulations in Table 2 show that, of the three founding EU member states, Italy (+ 1.3% more real GDP per year) profited more than the two other countries (France + 0.3%, Germany + 0.5%). However, the trade effect of participation in EU’s SM was greatest in Germany. Whereas the competition effect of the SM was positive in Germany and Italy, it was negative in France and dampened the overall growth effect.
1995 was the year of the last EU enlargement by rich countries when Austria, Finland and Sweden joined the EU. However, only the first two also introduced the Euro. Contrary to earlier studies (Breuss, 2020a; Oberhofer, 2019) that showed higher GDP effects of EU accession for Austria than for Finland and Sweden, this study identifies the highest growth effects in Finland and Sweden (each an increase of annual GDP growth of 1.2%). However, the trade effects are higher in Austria (Table 2).
Of the new EU member states covered in this study, Slovakia appears to have performed best. This is also a consequence of the introduction of the Euro. As far as the intra-EU trade is concerned, Bulgaria could profit more than the other member state. The problem with the simple EU model is that it is less stable for countries that have recently joined the EU (like Bulgaria, Rumania, and Croatia) and which also did not yet introduce the Euro. The model then only works with the membership dummy and can only capture a short period of EU membership.
Conclusions
The simple EU integration model presented herein captures the major features of economic EU integration (trade effects, competition effects and budgetary effects). Most comprehensive EU studies that use complex models with a variety of databases are not easily replicable. In contrast, this model, developed in EViews, uses readily available data. Therefore, replication of the model is possible. First, the simple EU model is sufficient for the evaluation of Austria’s EU membership. This prototype model is also capable of evaluating the EU integration effects of selected EU member states. It is flexible enough to deal with the complex EU history of the respective EU member states. Three of them are founding member states, The other countries became EU members later with and without introducing the Euro.
Notes
Badinger and Breuss (2011) provided an overview of studies that quantify the effects of Post-War economic integration.
The CGEBox permits simulation of the GTAP model in both Armington and Melitz versions. The Armington model is based on the premise that each country produces a different good and consumers would like to consume at least one of each country’s goods. The Melitz version considers firm heterogeneity, firm entry and exit in the industry as a whole, specific trade linkages, and love-of-variety effects by different agents, resulting in monopolistic competition.
The following simple EU model is a more compact version of the macroeconomic model evaluating the economic impact of 25 years of Austria’s EU membership developed by Breuss (2020a). The latter, also estimated in EViews, is more elaborate.
The EViews program and the dataset for Austria are available from the author on request.
After a long discussion, the EU finished the Services Directive (2006/123/EC), which was adopted in 2006 and implemented by all EU countries in 2009. The European Commission is now working with EU countries to further improve the single market for services (https://ec.europa.eu/growth/single-market/services/services-directive_en). A recent evaluation (Wolfmayr & Pfaffermayr, 2022) showed that not all the potentials of intra-EU services trade have been lifted.
More comprehensive evaluations of Austria ‘s EU membership show higher real GDP effects. Oberhofer (2019) with a structural gravity model approach (plus an input–output model ADAGIO) found that 20 years of EU membership (1995–2014) resulted in an annual real GDP growth of 0.7% and 40% more trade. Breuss (2020a) with a more extensive integration macro-model, found that 25 years of Austria’s EU membership resulted in additional real GDP growth of 0.8% per year.
References
Andersen, T. B., Barslund, M., & Vanhuysse, P. (2019). Join to Prosper? An Empirical Analysis of EU Membership and Economic Growth, KYKLOS, 72(2), 211–238.
Arriola, C., Benz, S., Mourougane, A., & van Tongeren, F. (2020). The trade impact of UK’s exit from the EU Single Market, OECD Economics Department Working Papers, No 1631. Retrieved November 18, 2020, from https://www.oecd.org/officialdocuments/publicdisplaydocumentpdf/?cote=ECO/WKP(2020)39&docLanguage=En
Badinger, H. (2007). Has the EU’s Single Market Programme Fostered Competition? Testing for a Decrease in Mark-up Ratios in EU Industries. Oxford Bulletin of Economics and Statistics, 69(4), 497–519.
Badinger, H., & Breuss, F. (2011). The Quantitative Effects of European Post-War Economic Integration. In M. N. Jovanovic (Ed.), International Handbook on the Economics of Integration, Volume III: Factor Mobility (pp. 285–315). Edward Elgar.
Baldwin, R., & Venables, A. J. (1995). Regional Economic Integration. VolIn G. M. Grossman & K. Rogoff (Eds.), Handbook of International Economics (Vol. III, pp. 1597–1644). Elsevier Science B.V.
Breuss, F. (2020a). 25 years of Austria’s EU membership, OeNB-SUERF 47th Economic Conference 2020a, 51–61. Retrieved August 29, 2022, from https://www.oenb.at/Termine/2020a/2020a-09-21-oenb-suerf-workshop.html
Breuss, F. (2020b). Die Europäische Union als Prosperitätsgemeinschaft („The European Union as a community of prosperity“), in: P.-C. Müller-Graff (Hrsg.), Kernelemente europäischer Integration (“Core Elements of European Integration”), Schriftenreihe des Arbeitskreises Europäische Integration e.V., Band 100. Berlin, 2020b, 301–336.
Britz, W. (2019). CGEBox—a flexible and modular toolkit for CGE modelling with a GUI, University of Bonn, Bonn: https://www.ilr.uni-bonn.de/em/rsrch/cgebox/cgebox_GUI.pdf. November 2019. Website: CGEBox, a CGE toolbox with a Graphical User Interface. Retrieved August 29, 2022, from https://www.ilr.uni-bonn.de/em/rsrch/cgebox/cgebox_e.htm
Britz, W., & Van der Mensbrugghe, D. (2018). CGEBox: A Flexible, Modular and Extendable Framework for CGE Analysis in GAMS Journal of Global Economic Analysis, 3(2), 106–177.
Cai, M., Canton, E., Cardani, R., Dierx, A., Di Dio, F., Pataracchia, B., Pericoli, F., Ratto, M., Rocchi, P., Rueda Cantuche, J., Simons, W., & Thum-Thysen, A. (2021). Modelling the macroeconomic impact of competition policy: 2020 update and further development, European Commission, Brussels, 2021 (With the contribution of Fabienne Ilzkovitz (ULB)). https://competition-policy.ec.europa.eu/system/files/2022-03/kdaq22001enn_macroeconomic_impact_of_competition_policy_2021.pdf. Accessed 29 Aug 2022
European Commission. (2022a). AMECO database. European Commission, Economy and Finance. https://economy-finance.ec.europa.eu/economic-research-and-databases/economic-databases/ameco-database_en. Accessed 29 Aug 2022
European Commission. (2022b). Operating budgetary balances. https://ec.europa.eu/info/publications/operating-budgetary-balance-gni_en. Accessed 29 Aug 2022
European Commission. (2022c). Competition Policy. https://competition-policy.ec.europa.eu/index_en
Felbermayr, G., Gröschl J., & Heiland, I. (2018). Undoing Europe in a New Quantitative Trade Model, ifo Working Papers 250. https://www.ifo.de/DocDL/wp-2018-250-felbermayr-etal-tarde-model.pdf. Accessed 29 Aug 2022
GTAP database. (2014). Global Trade Analysis Project. https://www.gtap.agecon.purdue.edu/. Accessed 29 Aug 2022
Gutiérrez, G., & Philippon, T. H. (2018). How European Markets became free: a study of institutional drift, NBER Working Paper Series, No. 24700, Cambridge, MA, June 2018. https://www.nber.org/system/files/working_papers/w24700/w24700.pdf. Accessed 29 Aug 2022
In’t Veld, J. (2019). The economic benefits of the EU Single Market in goods and services, Journal of Policy Modeling, 41(5, September-October), 803–818.
Ilzkovitz, F., & Dierx, A. (2021). Ex-post economic evaluation of competition policy: The EU experience, VOXEU_CEPR, 27 August 2020. Retrieved August 29, 2022, from https://voxeu.org/article/ex-post-economic-evaluation-competition-policy-eu
Jones, C. I. (1995). Time Series Tests of Endogenous Growth Models. The Quarterly Journal of Economics, 110(2), 495–525.
Kohler, W. (2004). Eastern enlargement of the EU: a comprehensive welfare assessment, Journal of Policy Modeling, 26(7), 865–888.
London Economics. (2017). The EU Single Market: Impact on Member States. Study commissioned by the American Chamber of Commerce to the EU (AmCham), London, 2017. http://www.amchameu.eu/sites/default/files/amcham_eu_single_market_web.pdf. Accessed 29 Aug 2022
Luhmann, N. (1997). Die Gesellschaft der Gesellschaft "The Society of Society“. Berlin, Germany: Suhrkamp-Verlag.
Mayer, T., Vicard, V. & Zignago, S. (2019). The cost on non-Europe, revisited, Economic Policy, 34(98), 145–199.
Mion, G., & Ponattu, D. (2019). Estimating economic benefits of the Single Market for European countries and regions, Policy Paper, Bertelsmann Stiftung. Gütersloh. https://www.bertelsmann-stiftung.de/fileadmin/files/BSt/Publikationen/GrauePublikationen/EZ_Study_SingleMarket.pdf. Accessed 29 Aug 2022
Oberhofer, H. (2019). Die Handelseffekte von Österreichs EU-Mitgliedschaft und des Europäischen Binnenmarktes ("The trade effects of Austria’s EU membership and the Common Market“). WIFO-Monatsberichte, 92(12), 883–890. https://www.wifo.ac.at/jart/prj3/wifo/resources/person_dokument/person_dokument.jart?publikationsid=62250&mime_type=application/pdf
Romer, P. M. (1990). Endogenous Technological Change, Journal of Political Economy, 98(5, Part 2), S71-S102.
Wolfmayr, Y., & Pfaffermayr, M. (2022). The EU Services Directive: Untapped Potentials of Trade in Services, FIW-Research Reports No. 03.https://fiw.ac.at/fileadmin/Documents/Publikationen/Studien2022/FIW_RR_03_2022_EU_Services_Directive.pdf. Accessed 29 Aug 2022
Funding
Open access funding provided by Vienna University of Economics and Business (WU).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Breuss, F. In Search of the "Right" Integration Effects: From Complex to Simple Modeling. Atl Econ J 50, 99–118 (2022). https://doi.org/10.1007/s11293-022-09751-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11293-022-09751-8