Introduction

Minimum wages have seen a remarkable return to the spotlight in 2015/2016, with the introduction of minimum wages in Germany and announcements of substantial minimum wage hikes in the UK and Japan. In this context, two questions become ever more relevant to policymakers: What are the benefits and costs of minimum wages? The first question produced a plethora of papers that agree that minimum wages decrease inequality but disagree on the size of this effect (e.g. Neumark and Wascher 2006; Manning 2003).

In contrast, the discussion of minimum wage costs yields strong disagreement. Empirical papers point to negative, positive or insignificant minimum wage effects on employment. The following analysis aims to tackle this question, where the focus is youth employment. The reason for the restriction to the younger age class is twofold. Firstly, the soaring youth unemployment in post-crisis Europe has become a pressing issue to policymakers. Secondly, minimum wages should have a more pronounced impact on young workers, since they are more likely to work in low-skill sectors (Manning 2003).

The present paper employs a fixed-effects panel data model covering 19 Organisation for Economic Cooperation and Development (OECD) member countries in order to estimate a nonlinear relationship between minimum wages and youth employment. In particular, it will be shown that the minimum wage effect on youth employment varies with labour market institutions. The motivation for considering nonlinearities follows Coe and Snower’s (1997) hypothesis that institutions form synergies in their interactions.

In the context of minimum wages, this hypothesis has only been thoroughly examined by Neumark and Wascher (2004). However, Neumark and Wascher’s paper suffers from the low quality of institutional variables. The present research paper employs better institutional and control variables as well as a larger number of observations. In doing so, significant negative synergies are estimated between minimum wages and institutions that enforce labour market rigidity such as unemployment benefits and union density, while a positive synergy is found with active labour market policies that constitute training for the unemployed.

Two key conclusions follow. Firstly, many minimum wage panel data models are misspecified as they omit the interactive term with labour market institutions, which might account for some of the discrepancy in empirical evidence. Secondly, policymakers need to consider the institutional setting faced before adjusting minimum wages. This paper suggests that minimum wage raises in rigid markets will depress youth employment particularly strongly.

Theoretical Background and Empirical Evidence

Economic Theory

Basic neoclassical theory suggests that, in a competitive labour market, minimum wages (MWs) above the efficient level will depress employment by decreasing labour demand. This effect will be more detrimental in low-skill sectors where MWs are binding. Given that young workers tend to work in such sectors, MWs lead to higher youth unemployment following this theory (Neumark and Wascher 2008).

However, more recent models dispute the validity of the neoclassical prediction. For instance, job search costs can engender monopsonistic markets in which firms can set wages below the competitive level without losing workers (Burdett and Mortensen 1998). In such a setting MWs can increase employment by limiting employers’ bargaining power (Manning 2003).

The implicit theoretical foundation of the following analysis diverges from both these theories. Firstly, it builds upon the distinction between supply and demand side effects as proposed by Brown et al. (2014). The authors argue that MWs raise labour supply by increasing the return on working, but depress labour demand through elevating costs faced by firms. Hence, the overall effect is ambiguous, but can potentially be investigated in greater detail by examining labour market institutions, broadly defined as the policies and conventions that determine the costs, flexibility and incentives of employment (Betcherman 2012). Coe and Snower (1997) argue that MWs can create synergy effects with other labour market institutions with respect to employment. In particular, the authors argue that institutions that make labour markets rigid, such as unemployment benefits, can aggravate the negative effect of MWs. This theory of policy complementarities or synergies will be empirically tested.

Review of Empirical Evidence

Empirical research with regards to the minimum wage effect on youth employment is rich but inconclusive. Earlier papers tend to confirm the neoclassical prediction of negative effects. For instance, Brown et al. (1982) find that a 10% increase in MWs decreases U.S. teenage employment by 1–3% in a time series study, which is confirmed in a later study by Neumark and Wascher (1992) for 16–24 year-olds for a U.S. panel dataset.

This consensus view was first challenged by Card and Krueger (1994). Using the 1992 New Jersey MW increase as a natural experiment, the authors found significant employment growth for restaurant employees in New Jersey compared to a control group in Pennsylvania. While this paper was criticised inter alia for the control group used (Neumark and Wascher 2006), it heralded the emergence of more papers questioning the former consensus. For instance, Dickens et al. (1998) rejected the null-hypothesis that MWs in the UK depress employment, while Christl et al. (2017) found positive employment effects for small MW increases.

Following Coe and Snower’s (1997) theory, the present paper argues that some of the conflicting evidence can be resolved by analysing policy complementarities. The first attempt to do so was conducted by Neumark and Wascher (2004), who found negative synergies between MWs and restrictive labour market policies in a panel analysis of 17 OECD countries. However, when analysing different groups of countries directly, the authors found that MWs have the most detrimental effect in liberal countries, which partially contradicts their former results. Another limitation is the reliance on time-invariant institutional variables. Despite the many questions that remain open after Neumark and Wascher’s analysis, few papers aimed to clarify the results and any synergies were at best included as an aside, if at all (Dolton and Bondibene 2011; Christl et al. 2017; Addison and Ozturk 2010). Hence, it is the aim of this research paper to dissolve some of the controversy discussed above by explicitly investigating potential synergy effects.

Data and Methodology

Data

The analysis is based on an unbalanced panel dataset of 19 OECD countries spanning the time frame 1985–2013, drawn from the OECD Labour Force Statistics and Minimum Wage Databases.Footnote 1 The dependent variable is the youth employment rate, defined as the ratio of the working population to the total population of 15–24 year olds.Footnote 2

The minimum wage variable is defined as the ratio of the minimum to median wage, dubbed the Kaitz index (KI). The KI can be interpreted as the relative price of unskilled to skilled labour. The median rather than mean wage is used in the denominator such that the KI does not change with the distribution of income.

The core of the analysis rests on the following four institutional variables, which are used to test Coe and Snower’s (1997) hypothesis of institutional complementarities:

  • The Employment Protection Index measures the costs of hiring and firing. It is constructed by the OECD based on eight items including severance pay and length of notice before firing. The indicator takes values between zero and six and is higher with stricter employment protection.

  • Union density is defined as the proportion of wage and salary earners covered by a union. This serves to approximate the bargaining power of incumbent workers (insiders).

  • Active labor market policies are designed to increase the competitiveness of unemployed workers and are measured as government expenditure as a proportion of GDP.Footnote 3

  • Unemployment benefit generosity is estimated by the OECD and defined as benefits received by an average production worker as a percentage of previous earnings.

Three control variables are used in all specifications. Firstly, the unemployment rate of 25–64 year-olds, harmonised by the OECD for better international comparability, is used as a labour demand control. Secondly, the number of 15–24 year olds as a proportion of the total working-age population serves as a supply-side control. Finally, purchasing power parity (PPP)-adjusted logged gross domestic product (GDP) per capita measures average worker productivity.

Methodology

The model specification is as follows:

$$ {emp}_{i t}=\beta {mw}_{i t-1}+{\mathbf{I}}_{\mathbf{it}}^{\mathrm{T}}\uppsi +{mw_{i t-1}}^{\ast }{\mathbf{I}}_{\mathbf{it}}^{\mathrm{T}}\Phi +{\mathbf{X}}_{\mathbf{it}}^{\mathrm{T}}\Theta +{\tau}_t+{\partial}_i+{\varepsilon}_{i t} $$

where emp it is the youth employment rate; mw it − 1 is the lagged minimum wage variable; \( {\mathbf{I}}_{\mathbf{it}}^{\mathrm{T}} \) is the transposed vector of institutional variables and ψ is the corresponding coefficient vector; \( {\mathbf{X}}_{\mathbf{it}}^{\mathrm{T}} \) are control variables; τ t are year dummies; and ∂ i are country fixed effects. The interactive coefficients between MWs and the institutions contained in the coefficient vector Φ are at the core of the analysis, as they capture Coe and Snower’s (1997) hypothesis of synergies.

MWs enter the regression in lagged form, as this is a way to break the potential two-way causality between MWs and employment: Governments might alter MWs in response to changes in employment levels. For similar reasons, unemployment benefits are lagged. In contrast, the remaining variables are included contemporaneously as they are unlikely to be endogenous to youth employment.Footnote 4

Note that while MWs are not exogenous to employment levels, they are likely to be conditionally exogenous. First, the inclusion of labour supply and demand variables already controls for how governments adjust MWs after employment shocks. Fixed effects further control for time-invariant characteristics that determine how different countries set MWs, which can include legislative and cultural reasons. This should strip out most non-random factors from the error term that simultaneously influence employment rates and MWs.

For these reasons, while an instrumental variable (IV) approach would certainly lend further credibility to the results, it does not seem to be necessary. Moreover, a convincing instrument has yet to be found. The most notable attempt was made by Dolton and Bondibene (2011) who instrument MWs with an index capturing how “left” a government is. However, the political orientation of governments is determined by voter preferences that are related to employment, which makes this method share the bias that it is trying to counteract.

Finally, note that country-clustered robust standard errors are employed, which control for unknown forms of serial correlation and heteroscedasticity (Wooldridge 2010). Failing to account for these factors can lead to downward-biased standard errors and the over-rejection of the null-hypotheses (Angrist and Pischke 2009).

Main Results and Cross-Country Analysis

Regression Results

Regression results are summarised in Table 1, whereby institutional variables were standardised by subtracting the mean and dividing by the standard deviation (s.d.) for greater comparability. The results indicate that MWs generally depress youth employment. At average institutional characteristics, the elasticity of the youth employment rate with respect to MWs is −0.24 (column 2), similar to Neumark and Wascher’s (2004) estimate of −0.16. More importantly, however, there is strong evidence for synergies in labour market institutions as three of the four interactive variables produce significant results. Since this forms the core hypothesis of the paper, each interaction is discussed in turn below.

Table 1 Regression results
Full size table

First, looking at the initial model specification (column 1), the interaction of MWs with employment protection is insignificant at 5%. This is not surprising following Bentolila and Bertola’s (1990) model of hiring and firing costs, which stresses that employment protection has two opposing effects. On the one hand, a firm’s inability to ascertain the productivity of prospective workers becomes more costly under high firing costs, to which firms respond with decreased hiring. However, it simply becomes harder to fire workers under high protection. Here it seems that these effects offset each other, rendering the interaction insignificant. Therefore this interaction will be omitted, yielding the preferred model in column 2.

Second, unemployment benefits produce significant negative synergies with MWs. Note that high benefits decrease the opportunity cost of unemployment, depressing the labour supply. Hence, in a high unemployment benefit regime, MWs fail to motivate workers to seek labour while increasing labour costs faced by firms.

Third, high union density also leads to a significantly aggravated minimum wage effect. Note that unions advocate for the protection of the workplace of insiders at the expense of job opportunities for outsiders (Kawaguchi and Murao 2014). Hence, when MWs are raised the jobs of non-unionised workers are disproportionately at risk. Now, young workers are less likely to be represented by unions, both because they have little knowledge of how unions work and because they are hardly targeted by unions (Keune 2015; Checchi and Nunziata 2011). Hence, MW effects on youth employment are worse under high union density.

In contrast, MWs interacting with active labour market policies (ALMPs) generate positive synergies. Recall that ALMPs primarily consist of training programmes for the unemployed. Hence, higher government expenditure on ALMPs should lead to a more productive and more motivated pool of job-seekers, providing employers with more suitable job applicants and decreasing labour market frictions. Furthermore, Scarpetta (1996) argues that ALMPs draw discouraged workers back into the labour force. Hence, under high ALMPs a raise in MWs increases the incentive to seek jobs while not substantially burdening employers who face more productive and better matching job applicants, leading to a positive synergy.

These results illustrate the importance of accounting for synergies between MWs and institutions. Hence, panel data models which omit interactive terms are misspecified and can lead to biased MW estimates. In the present discussion, omitting interactive terms (last column) leads to an estimated elasticity of youth employment to MWs of −0.36, much larger than that of the preferred model at average characteristics.

It also follows that policymakers cannot view MWs in isolation from other institutions. In particular, the results imply that unionisation and unemployment benefits should be viewed as policy substitutes to MWs, as they aggravate the negative demand side effect while depressing the positive supply side effect of MWs. The implication of these complementarities across different countries will be discussed in greater detail.

Cross-Country Analysis

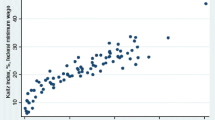
The analysis thus far suggests that the ideal setting for MWs consists of low unemployment benefits, low union density and high ALMPs. However, a country with these characteristics does not exist in practice. This is evident in Fig. 1, which plots countries according to their mean expenditure on ALMPs (y-axis) and a labour market fluidity index consisting of the mean union density and unemployment benefits (x-axis).Footnote 5 A high value of this index indicates a fluid labour market, i.e. low unemployment benefits and union density. Two similarly-sized camps of countries can be distinguished in Fig. 1: free-market economies with low ALMPs and low unemployment benefits or unionisation appear in the bottom right corner, while interventionist economies are positioned on the top left.

Fig. 1
figure 1

Classification of countries by mean expenditure on active labor market policies (ALMPs) and labor market fluidity. Data source: OECD Labour Force Statistics and Minimum Wage Databases; Nickell (2006); Gwartney et al. (2014); own calculations. The data spans the time period 1985–2013; for more details refer to online supplemental Appendix Table 1

Full size image

For the purpose of analysis, these two camps are again subdivided into two groups each. Group 1 consists of the most fluid markets (former soviet satellite states and Korea). Group 2 comprises the remaining free-market economies and consists mainly of traditionally liberal Anglo-Saxon economies. Interventionist countries subdivide into those with moderate and those with high market rigidity (groups 3 and 4, respectively).

Given this distribution of countries, a relevant policy question lies in assessing the cost of MWs across the two country types. An indicative answer to this question is provided in Tables 2 (groups 1 and 2) and 3 (groups 3 and 4), which show the implied marginal effects of MWs when plugging each country’s mean institutional characteristics into the preferred model of Table 1. The differences in predicted effects are striking. For the most restrictive countries (group 4), a one percentage point (p.p.) increase in MWs on average decreases the youth employment rate by a substantial 0.64 p.p, despite their high ALMPs. Meanwhile, for the most fluid labour markets (group 1) the effect is insignificant or even marginally positive, regardless of the low ALMPs. Hence, with the exception of France and Spain who have extremely high expenditures on ALMPs and are only moderately rigid, the model predicts interventionist countries to suffer more from MWs. This indicates that labour market rigidity as captured by unionisation and unemployment benefits is the defining factor determining the effect of MWs on youth employment.

Table 2 Implied marginal effect (ME) of minimum wages (MWs), free-market countries
Full size table
Table 3 Implied marginal effect (ME) of minimum wages (MWs), interventionist countries
Full size table

In order to confirm this hypothesis, the marginal effect across country types was directly estimated by allowing the slope of MWs to differ between free-market (groups 1 and 2) and interventionist (groups 3 and 4) countries as indicated by the model below:

$$ {emp}_{i t}=\beta {mw}_{i t-1}+{\mathbf{I}}_{\mathbf{it}}^{\mathrm{T}}\uppsi +\gamma {mw_{i t-1}}^{\ast }{ i ntervention}_i+{\mathbf{X}}_{\mathbf{it}}^{\mathrm{T}}\Theta +{\tau}_t+{\partial}_i+{\varepsilon}_{i t} $$

where intervention i takes the value 1 for interventionist countries and 0 otherwise, while the other variables remain as before. The estimated marginal effects are reported in Table 4 and show that the marginal MW effect on youth employment is insignificant at 5% for free-market but significant and negative for interventionist economies.

Table 4 Estimated marginal effect of minimum wages free-market versus interventionist countries
Full size table

Figure 2 summarises the policy implications of this section by plotting the implied marginal effect of minimum wages at each country’s mean institutional characteristics against labour market fluidity. Three simple policy lessons follow. Firstly, raising MWs in fluid labour markets should depress youth employment relatively mildly, if at all. Secondly, high economic costs of MWs in moderately rigid labour markets can be avoided by employing suitable ALMPs (France and Spain). Thirdly, this solution is not viable if labour markets are too rigid. Note that these conclusions oppose Neumark and Wascher (2004) where free-market countries were found to suffer more from MW increases.

Fig. 2
figure 2

Marginal effect of minimum wages (MWs) by labor market fluidity. Data source: OECD Labour Force Statistics and Minimum Wage Databases; Nickell (2006); Gwartney et al. (2014); own calculations. The data spans the time period 1985–2013; for more details refer to online supplemental Appendix Table 1

Full size image

Robustness Checks

Panel data studies in minimum wage research share two key characteristics: they comprise short time periods of few countries and rely on unbalanced datasets. This can bias both standard errors and coefficients. Nevertheless, these problems were not discussed in previous studies and are therefore addressed below.Footnote 6

Firstly, an unbalanced dataset is problematic if observations are missing non-randomly, since then data are selected based on unobservable characteristics, potentially biasing coefficients (Wooldridge 2010). This could be a problem in the present case as fewer observations are associated with less-developed countries. Now, it cannot be reasoned economically whether this panel imbalance will necessarily bias the interactive variables. This would occur if synergies work differently in countries with missing observations, for which there is no obvious reason. In order to examine whether the imbalance poses a problem, the analysis was repeated using a balanced subsample covering 2/3 of observations (Table 5, column 3). Note that the interactive coefficients are less than 1 standard error away from the original ones and remain significant. This does not rule out bias when using the full sample, but indicates that any bias is probably negligible.

Table 5 Main robustness checks
Full size table

Secondly, the small number of countries in the study is a potential problem for clustered standard errors as these are only consistent when the number of clusters approaches infinity (Angrist and Pischke 2009). A breach of this asymptotic condition can lead to downward-biased standard errors, as shown in Monte Carlo studies by Cameron et al. (2008). The authors recommend bootstrapping methods to counter this problem, since they constitute an asymptotic refinement and can decrease biases in finite samples. Essentially, bootstrapping works by drawing a large number of subsamples (with replacement) from the original data, estimating coefficients for each subsample and calculating standard errors based on the distribution of these coefficients (Angrist and Pischke 2009).Footnote 7 This method was adopted in column 2. Indeed, standard errors increase but the coefficients of the interactive variables remain significant, albeit the interaction with unemployment benefits is only at the 10% significance level. This indicates that the results are moderately robust to the problem of limited clusters, but availability of institutional data for more countries would solve this issue more thoroughly.

Conclusion and Limitations

Consistent with Coe and Snower’s (1997) hypothesis, MWs have been found to generate synergies with labour market institutions. In particular, restrictive institutions such as high union density and high unemployment benefits aggravate the negative impact of MWs, while active labour market policies create a positive synergy with MWs.

Two main conclusions follow. Firstly, the interactions between MWs and other labour market institutions are omitted relevant variables in many studies. This model misspecification could at least partially explain the large discrepancy in empirical results in the MW literature. Secondly, policymakers have to consider possible complementary effects when altering MW policies. In particular, the analysis indicates that MWs can be very costly in rigid labour markets with high union density and generous unemployment benefits.

There are some important limitations to the present analysis. First, only four institutional variables are incorporated and although the sample size exceeds that of most previous studies, data availability remains a problem. Moreover, while the low number of countries under analysis and the panel imbalance have been examined in robustness checks, these issues can only be fully resolved by incorporating more countries into the analysis.

Second, although there are reasons to believe that MWs are conditionally exogenous given suitable controls and fixed effects, a valid IV estimation would greatly improve the credibility of the analysis. This is an area with a large scope for improvement in MW research.

Last and perhaps most importantly, the economic costs of MWs are only one side of the token. Policymakers might be willing to sacrifice even large levels of employment in order to reap the benefits of MWs in the form of decreased wage inequality. However, whether the benefits of MWs exceed the costs remains a political and not economic debate. Nevertheless, this paper highlights that the costs can be very high in some settings in which MWs should be applied with caution.