Introduction

On the one hand, Leamer (2007) notes that eight out of ten post-war recessions in the U.S. were preceded by shocks to the housing sector. This number rises to nine, when we include the recent “Great Recession”. In this regard, Nyakabawo et al. (2015) stress the importance of housing prices shocks in particular. On the other hand, Hamilton (2008) indicates that nine of ten recessions in the U.S. since World War II have been preceded by an increase in oil prices. Interestingly, Hamilton (2009) even goes as far as arguing that a large proportion of the recent downturn in the U.S. gross domestic product (GDP) during the “Great Recession” can also be attributed to the oil price shock of 2007-2008. In this regard, Kaufmann et al. (2011) identified a significant long-run (cointegrating) relationship between household expenditures on energy and U.S. mortgage delinquency rates, and hence, postulate a direct role for energy prices in the 2008 financial crisis. In addition, Breitenfellner et al. (2015) analysed, using conditional logit models, the role played by energy inflation as a determinant of downward corrections in housing prices, based on a dataset 18 Organisation for Economic Co-operation and Development (OECD) economies spanning four decades. The authors provided strong evidence that increases in energy price inflation raised the probability of such corrective periods taking place.

Given this, an important research question is to analyse the many channels underlying the relationship between housing and oil prices:Footnote 1 (i) Oil price hikes adversely affect economic growth (as discussed above), and thus, dampen the demand for housing, and reduce the price; (ii) However, oil price increases are likely to increase construction and operational building costs, which might result in a decline in the supply of housing, thus pushing price up; (iii) If there is a tightening of monetary policy to curb the pressure induced by oil price increases on headline inflation, this is likely to withdraw liquidity from the housing market and hence, reduce housing prices through a fall in demand; (iv) However, if housing is used as an inflation-hedge, the inflationary-effect of oil prices might increase housing demand and hence, raise prices; (v) An increase in oil returns might also be associated with moving funds into the oil market at the expense of investment in housing as an asset, thus reducing price. So in summary, though an increase in oil price could either increase or decrease housing prices, depending on the strengths of the various channels, it is more likely that the negative impact is likely to dominate on average. Such a presumption has to do with the economy-wide negative impact generally associated with oil price hikes. But this remains to be empirically verified.

Against this backdrop, our paper investigates the time-varying interdependence between real housing returns and real oil returns for the U.S. economy over the annual period of 1859–2013, allowing for a set of control variables (economic growth, inflation and the interest rate) that are known to affect both these markets (Breitenfellner et al. 2015). Specifically, we construct time-varying measures of correlations between real housing market returns and real oil price returns based on the dynamic conditional correlation generalised autoregressive conditional heteroskedasticity (DCC-GARCH) model of Engle (2002). Taking into account both time variation and conditional heterogeneity in correlations, the proposed measure has several advantages compared to other commonly used indicators. For instance, it is able to distinguish negative correlations due to single episodes, synchronous behavior during stable years and asynchronous behavior in turbulent years. Unlike rolling windows, an alternative way to capture time variability, the proposed measure does not suffer from the so-called “ghost features,” as the effects of a shock are not reflected in n consecutive periods, with n being the window-span. In addition, under the proposed approach there is neither need to set a window span, nor loss of observations, nor is there a requirement for subsample estimation. To the best of our knowledge this is the first paper to analyse the time-varying relationship between real housing returns and real oil returns covering over 150 years of U.S. history, with the start date corresponding to beginning of the modern era of the petroleum industry with the drilling of the first oil well in the U.S. at Titusville, Pennsylvania in 1859.Footnote 2

At this stage, it is important to indicate the reasons behind our preference to use a DCC-GARCH approach rather than a time-varying vector autoregressive (VAR) method. First, as it is well-known, identifying shocks in a VAR would require us to order the variables. However, at an annual frequency, it is difficult to postulate which variable should be ordered first, i.e. is believed to be more exogenous. Of course, one could use various orderings and check for the robustness of the results. But then again, this would not guard against the possibility that the degree of exogeneity over such a long-span of data did not vary over time. An alternative approach would have been to use sign-restricted time-varying VAR, but this would take away from us the very essence of our exercise of deciphering the correlation between these two variables, which as indicated in the paper could be either positive or negative. In other words, one could not have, without doubt, imposed a theory-based sign either. Keeping these issues in mind, we decided to resort to a DCC-GARCH approach, which provides us with a time-varying correlation between these two variables accounting for heteroscedastic disturbances, without having to worry about the ordering of variables or sign-restrictions in a VAR model. Having said this, one limitation of our approach, given the long time-span of data, is our inability to control for other important variables (like macroeconomic and demographic) which are likely to affect both real housing and oil returns.Footnote 3 In such a multivariate setting, a VAR approach is preferable, as it also allows us to analyze the importance of the other variables (shocks) in the relationship between housing prices and oil price. Nevertheless, given that our concern is a time-varying analysis of correlation between these two variables, the DCC-GARCH framework can be considered most appropriate in the context of our study. The results of the empirical analysis reveal that comovements between housing and oil market returns are consistently negative over time, apart from periods of U.S. recessions during the 19th century, wherein correlations are positive.

Methodology

In order to examine the evolution of co-movements between real housing returns and real oil returns, we obtain a time-varying measure of correlation based on the dynamic conditional correlation (DCC) model of Engle (2002).

Let \(y_{t}=[y_{1t},y_{2t}]^{\prime }\) be a 2×1 vector comprising the real housing returns and real oil returns. The conditional mean equation of the model is then represented by:

$$ A(L)y_{t}=B(L)x_{t}+\varepsilon_{t}, \text{~ where ~} \varepsilon_{t}|{\Omega}_{t-1}\sim N(0,H_{t}), \text{~ and ~} t=1,...,T $$
(1)

where A and B are matrices of endogenous and exogenous variables, respectively, L the lag operator and ε t is the vector of innovations based on the information set, Ω, available at time t−1. The ε t vector has the following conditional variance-covariance matrix:

$$ H_{t}=D_{t}R_{t}D_{t}, $$
(2)

where \(D_{t}=diag{\sqrt {h_{it}}}\) is a 2×2 matrix containing the time-varying standard deviations obtained from univariate GARCH(p,q) models as:

$$ h_{it}=\gamma_{i}+\sum\limits_{p=1}^{P_{i}}\alpha_{ip}\varepsilon^{2}_{it-ip}+\sum\limits_{q=1}^{Q_{i}} \beta_{iq}h_{iq-q}, \text{~ ~} \forall i=1,2. $$
(3)

The DCC(M,N) model of Engle (2002) comprises the following structure:

$$ R_{t}=Q^{*-1}_{t}Q_{t}Q^{*-1}_{t}, $$
(4)

where:

$$ Q_{t}=(1-\sum\limits_{m=1}^{M}a_{m}-\sum\limits_{n=1}^{N}b_{n})\bar{Q}+\sum\limits_{m=1}^{M}a_{m} (\varepsilon^{2}_{t-m})+\sum\limits_{n=1}^{N}b_{n}Q_{t-n}. $$
(5)

\(\bar {Q}\) is the time-invariant variance-covariance matrix retrieved from estimating Eq. 3, and \(Q_{t}^{*}\) is a 2 ×2 diagonal matrix comprising the square root of the diagonal elements of Q t . Finally, \(R_{t}={\rho _{ij}}_{t}=\frac {q_{ij,t}}{\sqrt {q_{ii,t}q_{jj,t}}}\) where i,j=1,2 is the 2×2 matrix comprising the conditional correlations and which are our main focus.

Data

We use annual data, covering the period 1859-2013. Data for real GDP, Winans International nominal housing prices index for new homes, and West Texas Intermediate (WTI) oil prices are extracted from the Global Financial Database (GFD) (2015) database. The stock price index data come from GFD (2015), and the gold and silver price index data from Kitco (2015). The Consumer Price Index (CPI) used to deflate the housing, oil, stock, gold and silver prices to obtain the corresponding real values, is obtained from the website of Sahr (2015). The data on the short-term interest rate is obtained from Homer and Sylla (2005) over 1859-1870, and thereafter from the online data segment on the website of Shiller (2015). Barring the interest rate, all variables are converted to their growth rate forms (by taking the first difference of their natural logarithms) to ensure mean-reversion required for our DCC approach.Footnote 4 Given this, we lose one observation, and our effective sample covers the period of 1860–2013.

Empirical Findings

Table 1 reports the estimation results of the three bivariate DCC models. Panels A and B present the conditional mean and variance results, respectively, while Panel C contains the LjungBox Q-Statistics on the standardized and squared standardized residuals, respectively, up to 12 lags. The choice of the lag length of the autoregressive (AR) process of the conditional mean is based on the Akaike information criterion (AIC) and Schwarz Bayesian information criterion (BIC) and serves to remove any serial correlation in the standardized residuals. GDP growth, inflation and interest rates are also included in the conditional mean.

Table 1 Estimation results of DCC-GARCH model of real housing and oil returns, period: 1859–2013
Full size table

According to the results in returns in Table 1, we observe that increased economic growth leads to positive real housing returns and real oil returns, while increases in the inflation rate leads to negative real housing returns and increased real oil returns. Increases in the interest rate reduce real housing returns, but affect real oil returns positively. Barring the last result of the effect of the interest rate on the real oil returns, all results conform with the theory of housing and oil markets as discussed in the extant literature. The fact that a positive interest movement leads to an increase in real oil returns could be due to the fact that while nominal returns on both oil and inflation fell, the latter declined more. This line of reasoning makes sense, given that in the early part of the sample, the oil market was very volatile as it developed, and then from 1919 to 1976 the WTI oil price was administered. Moreover, a rise in real gold returns is associated with increased real housing returns and real oil returns, while a rise in real stock returns and real silver returns is associated with increased real housing returns and real oil returns, respectively. Interestingly, we observe that real oil returns take time to impact the real housing returns, in the sense that the second lag of real oil returns is more important than the first lag, both economically and significantly. This indicates that, on average, oil price movements take time to affect housing prices. The statistical significance of a and b coefficients (see panel B) suggests that dynamic correlations are indeed time-varying, and the model is well specified (as can be seen from panel C).

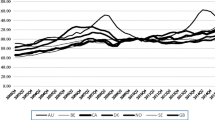
In Fig. 1, we present the corresponding dynamic conditional correlations of the model estimated in Table 1, along with their 90 % confidence intervals. The time-varying correlations between real housing and oil returns are consistently negative over time, apart from several recessions the U.S. economy experienced in the 19th century (i.e. 1865–67, 1874–78, 1896 and 1899–1900), wherein correlations become positive. During the 20th and 21st centuries, however, dynamic correlations between real housing and oil returns are consistently negative.Footnote 5 The fact that there is some evidence of positive correlation between real oil returns and real housing returns in the early part of the sample, especially during the recessionary episodes, indicates that, during these periods of recession, housing was probably acting as an inflation hedge to oil price increases which was the likely source of the recession in the first case. In addition, higher oil prices could have also resulted in higher construction costs and hence, higher housing prices as well. However, as both markets developed obtained financing and became more liquid, the more the standard negative correlation between real oil and housing returns was observed due to growth, monetary policy (liquidity), and investment channels, as discussed in the introduction.Footnote 6

Fig. 1
figure 1

Dynamic conditional correlations between real house returns and real oil returns. Note: Shading areas denote U.S. recessions as defined by the National Bureau of Economic Research (NBER) business cycles dating committee. Dotted lines denote the 90 % upper and lower confidence intervals. Source: Authors’ calculations based on data from Homer and Sylla (2005), GFD (2015), Kitco (2015), Sahr (2015) and Shiller (2015)

Full size image

Conclusion

In this study, we examine the dynamic comovements between housing and oil market returns in the U.S. over the period 1859–2013. Our empirical analysis reveals that comovements between housing and oil market returns are consistently negative over time, apart from periods of U.S. recessions during the 19th century, wherein correlations are positive. Moreover, we find that increased economic growth leads to positive real housing returns and real oil returns, while increases in inflation and interest rates lead to negative real housing returns and increased real oil returns, respectively. In addition, increased real gold returns lead to increased real housing returns and real oil returns, while a rise in real stock returns and real silver returns is associated with increased real housing returns and real oil returns, respectively. Using historical data comes at costs such as the quality of data, as well as its availability. However, we have guarded against these two issues by using data from reliable historical data sources, namely the Global Financial database and www.kitco.com. In addition, to avoid any bias due to missing variables, we have attempted to control for as many related variables as possible (contingent on data availability), that allows us to capture the theoretical channels relating real oil and housing returns. But, indeed, some influences from other important macroeconomic variables, like unemployment, and demographic variables, like fertility, are likely to be missing from our analysis. As part of future research, it would be interesting to extend our analysis by using a sign-restricted time-varying VAR model, which will allow us to identify the oil shocks properly, given that Kilian (2009) indicates that not all oil shocks are alike. We can also study the dynamic impact of oil shocks on housing prices over time using impulse responses functions.Footnote 7 This would, however, mean that we will need to use a shorter sample period, since the variables used to identify various oil shocks (supply, demand and precautionary), are only available post-World War II.