Introduction

Almost a century ago, Elton (1927) first explicitly defined the concept of the ‘food chain’, which is the simplest subset in a complex trophic network comprising numerous prey–predator relationships (Lindeman 1942; Hutchinson 1959). Since then, food web studies have been one of the central themes in ecology (their detailed history is reviewed in elsewhere, e.g., Layman et al. 2015). The food web is highly related to governing energy flows, driving population dynamics, concentrating toxic substances, and facilitating rapid evolution (Winemiller 1990; Kondoh 2003; Yoshida et al. 2003; Kelly et al. 2007). However, holistic descriptions of the food web are generally associated with considerable difficulties, such as the unlimited increase of prey–predator links with greater investigation effort (e.g., Polis 1991).

A food web can be described in at least three ways: as a connectedness web; energy flow web; and functional web (Paine 1980). Although the functional web cannot be tested without experimental manipulation of species (Paine 1980), the other two webs can be investigated by natural observation. The connectedness web, or the binary or qualitative web, describes the food web with nodes and links, with the main focus on population dynamics and inter-species competition for resources (Thompson et al. 2012). The connectedness web regards trophic networks as a collection of visible prey–predator relationships. In contrast, the energy flow web puts more emphasis on biomass transfer and productivity in a trophic network (Thompson et al. 2012). The energy flow web aims to quantify and integrate the degree to which biomass is transferred from one trophic unit (e.g., species) to another. Hereafter, this paper uses the viewpoint of the energy flow web.

The concept of a ‘trophic level’ (TL) is useful to describe both the connectedness web and energy flow web. The TL is a natural number, which starts from autotrophs (TL = 1) and corresponds with an animal’s feeding guild such as herbivore (TL = 2) and carnivore (TL ≥ 3). Animals that belong to the same TL are composed of biomass that has experienced an equal number of trophic transfers originating from their basal resources. The TL also corresponds well with the concept of a discrete consumer classification (e.g., primary consumer, TL = 2 and secondary consumer, TL = 3), which is usually applied to the food chain where an animal exclusively feeds on a diet that belongs to a single TL (Lindeman 1942; Hutchinson 1959). In contrast, the ‘trophic position’ (TP) is not always a natural number, as it reflects the average number of times that the biomass in an animal has been transferred through trophic pathways. For example, the TP of animals that get 50% of their energy from TL = 1 and 50% from TL = 2 is 2.5. In most natural settings, animals do not belong to a single TL, but show a unique TP, implying that they have more than one channel of trophic inflow (i.e., omnivores, Cummins et al. 1966; Thompson et al. 2007).

The stable isotopic compositions of nitrogen (δ15N) and carbon (δ13C) in the bulk tissues in organisms are known to be a good measure of their TP and food sources, respectively, which are crucial for understanding the food web structure (e.g., DeNiro and Epstein 1978; Minagawa and Wada 1984; Peterson and Fry 1987; Tayasu 1998; Vander Zanden et al. 1999; Post 2002). Over the past four decades, the δ15N and δ13C analysis has advanced greatly and has contributed to testing a number of ecological theories in food web science. Most of these advances also have important linkages with other disciplines, such as geochemistry and archaeology, where several new tools such as heavy element stable isotopes, radioisotopes, and compound-specific isotopes, have recently emerged. In particular, compound-specific nitrogen isotope analysis of amino acids (CSIA-AA) may be as a promising tool to estimate more precisely and accurately the TP of animals than the bulk stable isotope analysis (BSIA) (McClelland and Montoya 2002; Chikaraishi et al. 2007; McCarthy et al. 2007; Popp et al. 2007). However, the CSIA-AA methodology is still in its infancy, and there is a vast expanse of research field in trophic ecology to be addressed with this promising tool.

The aim of this paper is to review the potential of the CSIA-AA methodology for estimating not only TP, but also the diet sources of animals, with special emphasis on the physiological and ecological mechanisms of the trophic transfer. In particular, I propose three specific topics that may be addressed through the CSIA-AA technique: integrated trophic position, trophic transfer efficiency, and source mixing model. Finally, a guideline for data interpretation is shown to facilitate popularization of CSIA-AA into the future ecological community.

BSIA and CSIA-AA for TP estimation

Table 1 summarizes the BSIA and CSIA-AA methodologies for estimating the TP of animals in natural food webs. Detailed comments on the analytical procedures and biochemical basis for both methods is beyond the scope of this paper, and is holistically overviewed in elsewhere (e.g., Wada et al. 2013; Ohkouchi et al. 2015, 2017; McMahon and McCarthy 2016). In this paper, only the three most critical features of both the methods in the context of food web science were highlighted, as follows.

Table 1 Comparisons of BSIA and CSIA-AA for estimating the trophic position (TP) of animals
Full size table

Isotopic variation

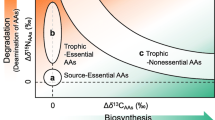
To estimate the TP of an animal, BSIA always requires isotope data for both the animal and its diet(s) (Table 1). This is because there is a large spatiotemporal variation in both the δ15N and δ13C of baselines (i.e., inorganic sources) that is reflected in primary producers and is propagated along the trophic pathways (Post 2002). Such variation sometimes exceeds the isotopic fractionation between the animal and its diet (hereafter, the trophic discrimination factor, TDF). To normalize isotopic variations in primary producers among different ecosystems, an internal offset is involved in the equation by incorporating the δ15N of the resource. In contrast, CSIA-AA does not need to characterize any diet source data to estimate the TP of the focal animal, because the TP value is represented as an offset between the δ15N values of glutamic acid (δ15NGlu), which increase considerably with TL, and phenylalanine (δ15NPhe), which remain unchanged during trophic transfer, in the animal (Table 1) (Chikaraishi et al. 2009).

Trophic discrimination

One of the most fundamental assumptions of both the BSIA and CSIA-AA methodologies for estimating TP is a constant TDF (Table 1). The TDF values of bulk δ15N (3.4 ± 1.0‰, Post 2002) and δ15NGlu (8.0 ± 1.2‰, Chikaraishi et al. 2009) are vital to estimate precisely and accurately the TP of animals. Both BSIA and CSIA-AA acknowledge that this isotopic fractionation primarily occurs during deamination or transamination of amino acids (Minagawa and Wada 1984; Chikaraishi et al. 2009). In animal metabolisms, digested protein is hydrolyzed into peptide, which is composed of a few amino acids. Among the 20 biogenic amino acids, glutamic acid plays a key biochemical role in making a variety of different molecules. One of the first steps of its catabolism is transamination with oxaloacetic acid to make aspartic acid catalyzed by glutamic-oxaloacetic transaminase (GOT) (Macko et al. 1986; Miura and Goto 2012). During this enzymatic reaction, the 15N-depleted amino group (–NH2) in the substrate (i.e., glutamic acid) is preferentially transferred into the product (i.e., aspartic acid) relative to the amino group enriched in 15N. Based on the Rayleigh fractionation model, this isotopic discrimination increases with the decreasing substrate with the isotopic fractionation factor of α, which is determined by a controlled enzymatic experiment. Goto et al. (2018) surmised that the transamination of glutamic acid has the α value of 0.9938 ± 0.0005 in vitro, and back-calculated that a 28% of glutamic acid should be converted to aspartic acid to realize an 8.0‰ TDF in the δ15NGlu (Table 1), with the assumption that GOT reaction is dominant in glutamic acid metabolism. These results also indicate that at least 72% of glutamic acid is catabolized to make α-ketoglutamic acid (i.e., carbon skeleton) and is dedicated to producing metabolic energy. It should be noted that the δ15NGlu value is controlled not only by GOT reaction, but also by other deamination/transamination reactions and de novo synthesis (Yamaguchi et al. 2017).

Source mixing

BSIA is highly sensitive to the mixing proportions of multiple resources with different isotopic compositions (Table 1). When the focal consumer is supported by more than one resource, BSIA needs δ15N data for all basal resources (if their TPs are known) that should be weighted by contribution of each resource in the consumer’s biomass. The δ13C value of the bulk tissues of organisms is often used to partition the diet sources contributing to the consumer of interest (e.g., Vander Zanden and Rasmussen 2001; Post 2002). On the other hand, a uniform profile in δ15NGlu and δ15NPhe for basal resources (i.e., β: + 8.4 ± 1.6‰ for vascular plants, e.g., terrestrial baseline; and − 3.4 ± 0.9‰ for non-vascular plants, e.g., aquatic baseline) is reported in CSIA-AA (Chikaraishi et al. 2010). Therefore, the common equation for CSIA-AA in Table 1 must be corrected with adjusted β only when both terrestrial and aquatic baselines are mixed in diet sources.

Future applications using CSIA-AA

In the previous sections, I briefly overviewed critical features of BSIA and CSIA-AA, and the potential of CSIA-AA for food web studies. Many ecologists have been less familiar with GC-C-IRMS than EA-IRMS, the latter of which enables a high throughput and large scale analysis. However, in addition to the three advantages mentioned above, the nitrogen amount required for CSIA-AA is approximately three-orders of magnitude smaller than that for BSIA, with a comparable analytical error (0.2–0.3 units) in the resulting TP estimate (Table 1). The question then arises, what can we explore in nature using this promising tool? How can we contribute to further development of isotope ecology? Below I identify some challenges which need to be addressed when using CSIA-AA in near future.

Integrated trophic position (iTP)

The advantage that CSIAA-AA does not need isotopic data from diet sources enabled Ishikawa et al. (2017a) to propose a new index named the integrated trophic position (iTP). The iTP is defined as the TP of a composite biomass of all organisms inhabiting a given area or space, as follows:

$${iTP = }\mathop \sum \limits_{i = 1}^{n} \left( {TP_{i} \times \frac{{B_{i} }}{{B_{T} }}} \right),$$
(1)

where TPi is the TP of species i, and Bi and BT are the biomass of species i and the total biomass of the focal community per unit area or space, respectively. The iTP is analogous with a multi-trophic ecosystem function, because a higher iTP indicates that basal resources are more effectively transferred to the top of the biomass pyramid. The iTP of macroinvertebrate communities in stream ecosystems was simply determined by their composite value of δ15NGlu and δ15NPhe, with no resource data, and ranged from 2.39 to 2.79 (Ishikawa et al. 2017a).

The iTP of stream macroinvertebrates was negatively correlated with species diversity, suggesting that biomass flow through trophic pathways decreased in more diverse communities (Ishikawa et al. 2017a). Similar patterns have been reported from ocean ecosystems (community average δ15N vs. species richness, Jennings et al. 2002) and lake ecosystems (food chain length: FCL vs. the number of endemic species, Doi et al. 2012). There are two possible hypotheses explaining this pattern (Fig. 1). First, the variance in edibility hypothesis predicts that inedible species will be more dominant in a more diverse community, which reduces biomass transfer through trophic pathways (Hillebrand and Cardinale 2004; Duffy et al. 2007). Second, the trophic omnivory hypothesis predicts that the TP of predators will decrease by increasing their omnivory in a more diverse community (Bruno and O’Connor 2005; Duffy et al. 2007). A comparison of the iTP with the TP of top predators (i.e., FCL) from multiple food webs may be useful to test the above two hypotheses. The FCL should be less sensitive to species diversity under the variance in edibility hypothesis, because the addition of inedible species does not interfere with biomass transfer from basal resources to top predators, whereas it does decrease the iTP. By contrast, the trophic omnivory hypothesis predicts that both the FCL and iTP should decrease with the decreasing TP of top predators in a more diverse community. Moreover, Kato et al. (2018) recently proposed three novel indices for food web diversity, which is based on reallocation of biomass from complex food webs to a simple food chain (Kato et al. 2018). Among their three indices, diversity of TL to which a species belongs (i.e., DR) is essentially related to the trophic omnivory hypothesis. Future research on the iTP should test the universality of the negative relationship with biodiversity and synthesize its relationship with other indices such as FCL or DR.

Fig. 1
figure 1

Modified from Ishikawa et al. (2017a)

Two possible mechanisms behind the negative relationships between biodiversity (as indicated by species richness) and the integrated trophic position (iTP) in stream food webs. a The variance in edibility hypothesis predicts that the biomass of inedible prey increases as the total number of species increases. b The trophic omnivory hypothesis predicts that the TP of top predators decreases by feeding on prey that belong to more than one TL as the total number of species increases. In biomass view, the width of grey bars indicates the biomass of each trophic level (layer).

Full size image

The iTP index may also be expanded to other disciplines, including fisheries science and demography. For instance, Pauly et al. (1998) revealed that the average TP value of commercial marine fish has declined from 3.3 to 3.1 since the 1970s, due to overexploitation of fish with high TP values. In contrast, the global mean TP value of human beings has gradually increased from 2.15 to 2.2 since the 1970s, suggesting that our food preference has shifted slightly from herbivorous to carnivorous diets during the last half century (Bonhommeau et al. 2013). Because these TP values were estimated from stomach contents or published databases, the observed variation might be different from that based on the stable isotope analysis, which takes account of energy flow along trophic pathways. Therefore, it may be interesting to explore the iTP of fisheries landings and human beings using CSIA-AA. This will be useful as fundamental information to predict the maximum population size of both animals and human beings on the Earth, under the constraint conditions of resource production, energy transfer efficiency, and ongoing biodiversity loss.

It should be noted the iTP estimation relies on two important assumptions, although it has not been applied yet by other researchers since Ishikawa et al. (2017a). First, the TDF is assumed as a constant (Table 1) (Chikaraishi et al. 2009). As mentioned in the section “Trophic discrimination”, the TDFGlu value depends on both the enzymatic (e.g., GOT) activity and the total flux of catabolized glutamic acid. Some recent studies have suggested a potentially considerable variation in TDFGlu across a variety of organisms (e.g., McMahon and McCarthy 2016). However, a rigorous controlled feeding experiment using stream-dwelling dobsonfly larva (Protohermes grandis) indicates that its observed range of TDFGlu − TDFPhe (7.1 ± 0.5‰, n = 3) has a good agreement with the published value (7.6 ± 1.3‰) (Chikaraishi et al. 2009), implying that unusual TDFGlu is not likely to be the case in stream macroinvertebrate communities (Ishikawa et al. 2017b). Second, the iTP estimate for stream macroinvertebrates in Ishikawa et al. (2017a) used the β value of − 3.4‰, which did not take account of the mixing proportion of terrestrial and aquatic resources (Table 1). Therefore, their iTP values might be underestimated if the incorporation of terrestrial organic matter (e.g., leaf litter) with the β value of + 8.4‰ into stream food webs was significant (see also the section “Source mixing”). However, the negative relationship between biodiversity and iTP was still evident even when the analysis excluded headwater ecosystems where terrestrial resources made a greater contribution to the biomass of stream macroinvertebrates (Ishikawa et al. 2017a).

Trophic transfer efficiency (TTE)

The metabolic transfer within individual animals is a phase of the energy transfer in ecosystems, where primary producers (TL = 1) support all heterotrophs (TL ≥ 2). In a steady state, a portion of biomass production is transferred into a higher TL through a trophic flow, and the TTE is defined as biomass in TL (n) divided by that in TL (n − 1), assuming a constant biomass stock per unit energy flow across all TLs. Theoretically, the TTE is divided into three components (Kozlovsky 1968; Odum 1968; Burns 1989; Strayer 1991; Chapin et al. 2011): consumer production efficiency PE (consumer production/assimilation), assimilation efficiency AE (assimilation/ingestion), and consumption efficiency CE (ingestion/resource production), expressed as the following equation:

$$TTE = {PE} \times {AE} \times {CE} = \frac{Consumer\,production}{Resource\,production}.$$
(2)

The PE decreases with decreasing body size (i.e., increasing surface to volume ratios) due to a greater heat loss, or with increasing age due to a lower growth rate of the consumer individual (Chapin et al. 2011). The AE is determined by the food quality in the consumer’s stomach or gut. A higher AE is expected in more suitable nutritional compositions for, or less stoichiometric imbalance with, the consumer’s demand (Chapin et al. 2011). It is also suggested that AE increases with more easily digestible foods such as prey organisms without hard shells. The CE is affected by the population density or biomass of diet organisms (i.e., foods for the focal consumers). A higher CE is expected in consumers that have more available foods in their habitat (Fig. 2) (Chapin et al. 2011). Energy is produced by catabolizing a portion of the assimilated fraction, which is ultimately lost as heat or respired CO2. In contrast, some undigested prey for the consumer may be broken down by microbes and added to the assimilation flux. This ‘brown food chain’ may increase AE, which is particularly important in oligotrophic environments such as terrestrial ecosystems (Haraguchi et al. 2013; Hyodo et al. 2015).

Fig. 2
figure 2

Simplified scheme illustrating three representative components (PE production efficiency, AE assimilation efficiency, CE consumption efficiency) in trophic transfer efficiency TTE (Chapin et al. 2011). The trophic discrimination factor (TDF) is expected to decrease with increasing PE based on the Rayleigh fractionation model. In contrast, it is hypothesized that TDF increases with increasing AE due to a greater contribution from detrital (microbial) input to assimilation flux. In theory, TDF and CE should not have any correlation. See Eq. (2) and text for details

Full size image

The CE is unlikely to be affected by the metabolic process and is unrelated to TDF. It is possible that AE increases TDF by decreasing PE when the microbial intervention is significant. Indeed, this hypothesis is supported by recent studies that showed that the presence of microbes adds one more TL (Steffan et al. 2015; Yamaguchi et al. 2017) between consumer and prey, and apparently increases TDF. It should be noted that when microbes also incorporate inorganic nitrogen to synthesize new amino acids, TDF may rather decrease (Yamaguchi et al. 2017). Among the three components, PE is most directly connected to TDF. Under a constant enzymatic activity (i.e., α = 0.9938), TDFGlu is 8.0‰ when PE is 28%, and TDFGlu increases with decreasing PE (Fig. 2) (Goto et al. 2018). Values of TDFGlu lower than 8.0‰ are expected for consumers with a higher production flux (i.e., PE’s numerator) (McMahon and McCarthy 2016) or consumers with a lower assimilation flux (i.e., PE’s denominator) (Chikaraishi et al. 2015). In contrast, values of TDFGlu higher than 8.0‰ are expected for consumers with a PE lower than 28% (i.e., lower production flux and/or higher assimilation flux) (McMahon et al. 2015). According to published data on controlled feeding experiments that were summarized in McMahon and McCarthy (2016), the TDFGlu value ranged from 0.3 to 19.4‰ among various combinations of consumer and prey, which is equivalent with 0.5–95% in PE (Goto et al. 2018), if the microbe-mediated effect is not considered. It should be noted that consumers (dobsonfly larvae) with no ingestion flux (i.e., starved) show a nearly normal TDFGlu value of 7.5 ± 0.5‰ (n = 5), suggesting that their metabolic energy is compensated by catabolizing storage lipids or carbohydrates (Ishikawa et al. 2017b). Although the TDFGlu value is not directly interchangeable with TTE, it has the potential to be a proxy for PE and AE in food webs.

The TTE indicates biomass yield per unit production and strongly relates to a multi-trophic ecosystem functioning (Duffy et al. 2007; Wang and Brose 2017). Although the dynamic range of TTE may not be very great in nature (e.g., 10 ± 5.8% for marine food webs, Pauly and Christensen 1995), several studies have reported a negative (e.g., Barnes et al. 2010) or positive (e.g., Sanders et al. 2016) relationship between TTE and TP. Energetics predict that species body mass increases with decreasing biomass per unit production (Brown and Gillooly 2003), which may result in an apparent negative relationship between TTE and TP (Barnes et al. 2010). In contrast, the positive relationship may be explained by the fact that carnivores tend to have higher PE than herbivores, because the nutritional composition of carnivores and their diets (e.g., herbivores) is more similar than that of herbivores and their diets (e.g., algae) (Floeter et al. 2005). Future CSIA-AA studies based on both field and laboratory experiments should help to estimate the spatial and temporal variations in TTE and TDFGlu among a variety of ecosystems to test the classical hypothesis that TTE is 10% in every ecological community (Kozlovsky 1968; Odum 1971).

Source mixing model

Animals tend to feed on more than one prey or food source in most cases. To estimate the relative contribution of each resource to the focal consumer, an isotopic mixing model is sometimes used. For example, Fig. 3a schematically illustrates that both the δX (e.g., δ13C of bulk tissue or δ15NPhe) and δY (e.g., δ15N of bulk tissue or δ15NGlu) values of consumers are on the mixing line of resources A and B. In this case, the relative contribution of the two resources to this consumer is consistently estimated between the two isotopes. Researchers may consider at least four possibilities when they meet the case shown in Fig. 3b. First, there might be another unknown resource that is missing in this window. The missing resource might have higher δX and lower δY values than those of resources A and B, and this unknown resource might contribute substantially to the diet of the consumer. Second, the isotopic variation in resources A and/or B might be greater than the standard deviation in this plot. Researchers might fail to collect a sufficient number of samples for statistical robustness, and thus the isotopic variation in resources may be underestimated.

Fig. 3
figure 3

Mixing model examples a, b that illustrates a consumer (grey) and its two distinctive resources (black and white). The linear mixing model works in a, whereas it does not work in b. Note that the trophic discrimination factor (TDF) is set at zero in a and b. c When the diet composition of prey is homogeneous, the isotopic routing does not affect output of the mixing model. d When the diet composition of prey is heterogeneous, isotopic routing may complicate the mixing model. e When the turnover time of each component (element or compound) is homogeneous, all dietary tracers show the same estimate in the mixing model at certain times. f When the turnover time of each component is heterogeneous, different dietary tracers may show different estimates in the mixing model at certain times. The shapes and colors of the symbols indicate different dietary tracers and their isotopic compositions, respectively

Full size image

Third, there might be an ‘isotopic routing effect’ on the consumer’s metabolism (Schwarcz 1991; Phillips and Koch 2002) (Fig. 3c, d). The linear mixing model with more than one isotope assumes that different elements, nutrients, or compounds in multiple resources are disassembled and reassembled in consumers in a same fashion with the resources (Phillips et al. 2014) (Fig. 3c). This is unrealistic in mixed ecosystems such as freshwater ecosystems, where terrestrial and aquatic resources with a very different food quality (e.g., C/N ratios) contribute to consumers’ diets. For simplicity, let a given consumer (e.g., omnivorous macroinvertebrates) in stream ecosystems assimilate 80% of carbon from leaf litter (terrestrial TP = 1) and 20% from algal grazers (aquatic TP = 2), but 50% of nitrogen from leaves (nitrogen-depleted source) and 50% from grazers (nitrogen-enriched source). The TP value of this omnivore would be estimated by carbon as 2.2, but by nitrogen as 2.5 (Fig. 3b). A discrepancy could occur when the consumer obtains carbon mainly as a carbohydrate (e.g., sugars) or lipids, which is abundant in leaves, but nitrogen as a protein, which is more enriched in animal biomass (Fig. 3d) (Fry and Sherr 1984). This effect potentially complicates the linear mixing model using BSIA, but has often been underestimated (Gannes et al. 1997; Wolf et al. 2009). To minimize this isotopic routing effect on the TP estimation of animals, some mixing model packages (e.g., SIAR) consider the stoichiometric imbalance among diets by weighting the estimate with the elemental concentration of each resource (e.g., Parnell et al. 2010). However, the elemental concentration is not necessarily proportional to consumers’ growth because their AE may be adjusted depending on food quality (Urabe et al. 2018). Furthermore, most researchers separately use bulk δ13C to partition diet sources and bulk δ15N to estimate TP (e.g., Vander Zanden and Rasmussen 2001; Post 2002), because the TDF of the former is smaller than that of the latter (Table 1). In such a case, the isotopic routing effect must be seriously considered, whatever the mixing model that is applied.

Finally, the turnover time of dietary tracers (elements or compounds) might be of importance (Fig. 3e, f). If the focal consumer is captured and analyzed before its biomass is completely replaced with its current diet, some tracers may already reflect the new diet but others may retain vestiges of its previous diet (Fig. 3f). In such a case, the combined use of multiple dietary tracers with different turnover times is problematic. The BSIA method integrates mixed isotopic compositions of different elements (e.g., carbon vs. nitrogen), compounds (e.g., carbohydrate vs. amino acid), and tissues (e.g., muscle vs. liver) in the organism, all of which show unique turnover times from days to years (Vander Zanden et al. 2015). The use of BSIA is associated with numerous biochemical and physiological assumptions that must be made a priori to consider the size of any potential isotopic shift within the organism, as well as between basal resources and consumers (DeNiro and Epstein 1978). These factors may potentially provide misleading outputs from the mixing model, or results that contradict prior information (e.g., animals’ stomach contents) or, in the worst case, a wrong conclusion, as illustrated in Fig. 3b. In contrast, CSIA-AA is less sensitive to both the isotopic routing and the turnover effects than BSIA, because: (1) animal nitrogen is derived mainly from diet amino acids, whereas their carbon is derived not only from amino acids, but also from other sources such as carbohydrates and lipids in their diets (Ohkouchi et al. 2015), and (2) the δ15N of most amino acids shows a similar turnover time (monthly scale) within animal muscle (Braun et al. 2014).

Unfortunately, the current CSIA-AA methodology cannot estimate the precise TP of animals inhabiting an ecosystem where both vascular and non-vascular plants contribute to basal resources, without knowledge of the relative proportions of each resource in the focal animal. This is because vascular and non-vascular plants have distinctive β values (Table 1). Most freshwater and seagrass meadow ecosystems are included in these systems because the former are supported by terrestrial higher plants and algae/cyanobacteria, and the latter are supported by seagrass, which belongs to the vascular plants group, and sea algae. The β value of animals in these systems should be corrected using animal-specific mixing proportions of vascular and non-vascular plants before calculating their TP. Without calculating mixing proportions, the TP values of sea turtles, polychaeta, and some stream macroinvertebrates are significantly underestimated (Arthur et al. 2014; Ishikawa et al. 2014; Choi et al. 2017). However, the β value correction requires an excessive δ15NGlu and δ15NPhe measurement of potential resource data, which diminishes the advantage of CSIA-AA.

To solve this problem, another amino acid such as methionine (Met) would be useful because the δ15N of Met (δ15NMet) relative to δ15NGlu is not different between vascular and non-vascular plants (Ohkouchi and Takano 2014), unlike the δ15NPhe relative to δ15NGlu (i.e., β value). This is primarily because vascular plants transaminate Phe for use as a building block of lignin phenols, which increases the δ15N of remaining Phe, while Met is not transaminated by either vascular and non-vascular plants (Chikaraishi et al. 2007; Ohkouchi and Takano 2014; Ohkouchi et al. 2015). The use of the δ15N values for these triple amino acids, therefore, should be further validated in various organisms including sea turtles, polychaeta, and some stream macroinvertebrates to provide an accurate TP estimate of animals inhabiting mixed ecosystems.

Synthesis and closing remarks

This paper conceptually reviewed the three topics in food web science that can be addressed by CSIA-AA in future studies. These topics are not mutually independent, and are tightly interconnected. For example, if the decrease of iTP occurs under the variance in edibility hypothesis, the increase of inedible prey will result in decreasing CE. In contrast, under the trophic omnivory hypothesis, CE will increase in more diverse communities with decreasing inedible prey. If PE and AE remain constant in these two cases, the relationship between TTE and biodiversity may be negative and positive under the variance in edibility hypothesis and the trophic omnivory hypothesis, respectively. However, the negative relationship between the iTP and biodiversity must be revised if the TDF significantly varies among communities. Since the TDF is in inverse proportion to the TP (or iTP) (see the common equation in Table 1), the TDF has an apparently positive relationship with biodiversity. An increase in the TDF can be explained by decreasing PE and/or increasing AE (Fig. 2). The PE is determined in organismal metabolisms and is unlikely affected by biodiversity. Thus, AE should be responsible for increasing TDF in more diverse communities through detrital contributions. Given that PE and CE remain constant, this suggests a positive relationship between TTE and biodiversity, which supports the trophic omnivory hypothesis. These ideas are all speculative at the moment, but will be worth testing in further studies to understand the role of biodiversity on multi-trophic ecosystem functioning.

After the seminal work executed by Minagawa and Wada (1984), stable isotope techniques including BSIA have contributed significantly to the development of trophic ecology. Surprisingly, their early data suggested that a great isotopic discrimination of nitrogen occurred during amino acid metabolism (i.e., deamination/transamination), and they had already the foresight to predict the potential of CSIA-AA for food web science. Since it is a relatively new methodology, several assumptions are associated with the equation that is used for TP calculation. Figure 4 summarizes an example of the flow diagram with the relevant references for interpreting the TP estimate using CSIA-AA. The methodology will be improved with further exploration of the universality/variability of some key components such as TDF and β values in different ecosystems (Nielsen et al. 2015; McMahon and McCarthy 2016). For example, it has been suggested that cultivated leguminous plants have an unusual metabolic pathway of amino acid biosynthesis, which may result in a different β value from that of other autotrophs (Styring et al. 2014). It is also possible that the TP estimate of flowers (TP=2) is higher than that of leaves (TP=1), suggesting that blooming is trophically analogous with predation (Takizawa et al. 2017). Furthermore, to establish the TDF more accurately, some recent studies recommend the use of multiple amino acids (e.g., Bradley et al. 2015) or a non-linear equation (e.g., Hoen et al. 2014) (Fig. 4). In order to reduce errors associated with the TP estimate and putative diet menu of the focal organism in nature, I suggest researchers do a step-by-step screening for all possibilities based on prior information (e.g., literature survey) or controlled experiments (e.g., feeding trials). In addition to the methodological refinements, a theoretical modelling approach is missing in current CSIA-AA research, and this will be indispensable to pursue next-generation food web science.

Fig. 4
figure 4

Flow diagram to help with interpretation of the TP estimate using the CSIA-AA methodology. Numbers correspond to the following references: (1) Styring et al. (2014); (2) Ishikawa et al. (2014); (3) Germain et al. (2013); (4) Takizawa et al. (2017); (5) McMahon et al. (2015); (6) Bradley et al. (2015); and (7) Hoen et al. (2014)

Full size image

Finally, the TP estimate based on the energy flow web is not necessarily the same with the one based on the connectedness web. In the connectedness web, a ‘mouth-to-mouth’ TP value for animals is defined as the sum of the binary links (0 or 1) from an animal through all its prey down to the basal resource(s). It does not take into account the prey ingested but not digested in the animal’s stomach (Fig. 2). Optical identification or DNA metabarcoding of stomach contents are the most straightforward approaches to unravel ‘who eats who’ in trophic networks (e.g., Kartzinel et al. 2015; Nielsen et al. 2018). In contrast, the TP value in the energy flow web instead indicates ‘who assimilates who’ and enables the estimation of the average number of times that the organic matter is transferred from basal resource(s) to the animal of interest (Post 2002). The TP estimate in the energy flow web may be quite different from that in the connectedness web when AE and/or CE in Fig. 2 are very low and prey organisms exhibit various TPs. The two approaches sometimes cause confusion by showing an inconsistent contribution of prey to the consumers, especially in complex food webs where consumers are supported by dozens of prey organisms (Nielsen et al. 2018). Furthermore, most animals drastically shift food preferences during their lifespan (Graham et al. 2007). Therefore, the TP estimate based on any methods including CSIA-AA does not correspond closely with the ‘real TP’ of animals, which may be integrated using all possible dietary tracers from multiple tissues with different turnover times.