Abstract
Elucidating the mechanism shaping the spatial variations of traits has long been a central concern of evolutionary biologists. Geographic clines of allele/morph frequencies along environmental gradients are suggested to be established and maintained by the balancing of two opposing evolutionary forces, namely selection that generates spatial differentiation in morph frequencies, and selection and/or stochastic factors that lead to the coexistence of multiple morphs within a population. Thus, testing for both selection and stochastic factors is necessary for a comprehensive understanding of the mechanism underlying clinal variation in morph/allele frequency in natural populations. Here, I identified the evolutionary forces responsible for clinal variation of color morph frequency in Ischnura senegalensis by comparing the population divergence of putatively neutral loci generated by high-throughput next-generation sequencing (F STn) with that of the putative color locus (F STc). No strong correlation was observed between F STn and F STc, suggesting that stochastic factors contribute less to color-locus population divergence. F STc was less than F STn between populations exposed to similar environmental conditions, but greater than F STn between populations exposed to different environmental conditions, suggesting that both balancing selection and divergent selection act on the color locus. Therefore, two antagonistic selection factors rather than stochastic and historical factors contribute to establishing the clinal variation of morph frequency in I. senegalensis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Elucidating the factors that affect spatiotemporal variations of traits has long been a central concern of evolutionary biologists (Endler 1977). Spatial variations of genotype or allele frequencies may provide direct evidence of the forces driving microevolution, that is, selection and random genetic drift (Wright 1943; Endler 1977). In addition to these microevolutionary aspects, increased phenotypic diversity has been suggested to enhance population performance (e.g., population productivity, stability, and sustainability), which can reduce the risk of extinction and thereby influence macroevolutionary dynamics (Forsman et al. 2008; Wennersten and Forsman 2012; Takahashi et al. 2014a). The coexistence of multiple morphs can also promote the use of diverse environmental resources and enhance population stability and colonization success (Forsman et al. 2008). Spatiotemporal variation in population processes is thus partly explained by inter-population variation in phenotypic diversity. Elucidation of the nature and mechanisms of spatial variation in morph/allele frequency can contribute to an understanding of the spatiotemporal demographic dynamics of populations, communities, and ecosystems, as well as their evolutionary potentials, speciation processes, and macroevolutionary dynamics (Wennersten and Forsman 2009, 2012).
Spatial variation of neutral and nearly neutral genetic variation typically results from genetic drift, migration, and historical events, with genetic differentiation then tending to increase with geographic distance, a phenomenon referred to as “isolation-by-distance.” In contrast, spatial differentiation of fitness-related genetic variation is mainly affected by selection associated with an environmental gradient or heterogeneity. In practice, morph frequency variations in visible polymorphisms are strongly correlated with environmental conditions such as temperature, humidity, and biotic factors (Schemske and Bierzychudek 2007; Saccheri et al. 2008; Brakefield and de Jong 2011; Takahashi et al. 2011, 2014b). Nevertheless, morph frequency variation in these traits can be clearly affected by stochastic factors such as genetic drift, gene flow, and historical events (Iserbyt et al. 2010).
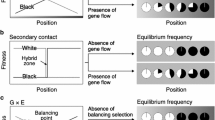
Geographic clines of allele/morph frequencies along environmental gradients have been observed for many species (Komai et al. 1950; Cook et al. 1986; Itoh 1991; Schemske and Bierzychudek 2007; Hammers and Van Gossum 2008; Hodgins and Barrett 2008; Cooper 2010; Gosden et al. 2011; Cook and Saccheri 2012). Such geographic clines are established and maintained by the balancing of two opposing evolutionary forces, namely, selection that generates spatial differentiation in morph frequencies, and selection and/or stochastic factors that lead to the coexistence of multiple morphs within a population (Endler 1977). Selection that induces spatial variation in morph frequencies is referred to as divergent selection and is mainly derived from gene-by-environment interactions. In a situation where the fitness of each morph changes differentially along an environmental gradient, relative fitness changes and sometimes reverses across a balancing point at which each morph shows equal fitness (Slatkin 1973; Endler 1977). Such divergent selection can lead to spatial differentiation in morph frequency; however, the frequency does not change smoothly along the environmental continuum because only a single morph having the highest fitness should dominate each population over an evolutionary period of time (Endler 1977; Takahashi et al. 2011). Consequently, divergent selection per se leads to an all-or-nothing pattern in morph frequency across the balancing point.
The evolutionary forces that enhance the maintenance of multiple morphs within a population must establish a smooth cline of morph frequency along the environmental continuum. Gene flow among populations experiencing different environmental conditions can lead to the coexistence of multiple morphs within a population around a balancing point, with a morph frequency cline established along the environmental gradient (Slatkin 1973). This type of cline is maintained on an evolutionary time scale by the balance between local directional selection and immigration of maladaptive alleles/morphs (i.e., migration–selection balance). Balancing selection, such as negative frequency-dependent selection and overdominant selection, can also lead to the coexistence of multiple morphs within a population (Endler 1973). The balance between local directional selection and balancing selection within a population (selection–selection balance) can establish a morph frequency cline in a certain geographic range across the balancing point.
Alternatively, a morph frequency cline is potentially observed after secondary contact among historically allopatric populations with different alleles (Latta and Mitton 1999; Whibley et al. 2006). When two populations without any reproductive barriers come into secondary contact, the boundary populations constitute two morphs, and a morph frequency cline is thus temporarily established around the hybrid zone. Most of the clinal differences in morph frequency will be transient, however, as the morph with the highest fitness in each population will outcompete the other if there is a fitness differential. Even if the two morphs have identical fitness, variation in morph frequency will disappear over evolutionary time unless there is a common morph advantage preventing introgression (Mallet and Barton 1989).
To summarize, the potential evolutionary forces that establish stable/temporal morph frequency clines are divergent selection, balancing selection, gene flow, and historical events, with the relative contributions of these factors shaping clinal variation in morph frequency. In some cases, population genetic analyses have demonstrated the contribution of stochastic and historical factors, but the presence of balancing selection has not been tested (Cheviron and Brumfield 2009; Kazancıoğlu and Arnqvist 2013). In other cases, fitness analyses have suggested the influence of two types of antagonistic selection—divergent selection and balancing selection—and ruled out the contribution of historical events (Takahashi et al. 2011). It is thus necessary to test for selection factors, such as divergent and balancing selection, as well as stochastic factors, such as stochastic drift, gene flow, and historical events, to obtain a comprehensive understanding of the mechanism underlying clinal variation in morph/allele frequency in natural populations.
Comparison of the population differentiation of neutral loci vs. loci governing a focal trait is a common method of detecting the influence of selection and stochastic factors on population divergence of traits in nature (McKay and Latta 2002). To obtain insights into the contribution of divergent selection, balancing selection, gene flow, and historical events to population divergence of loci suspected of governing a focal trait, the degree of genetic differentiation between populations (e.g., F ST) at those loci can be contrasted with the degree of differentiation at neutral loci (Gillespie and Oxford 1998). For example, divergent selection, balancing selection, and no selection are suggested to be acting if log10[F ST (focused)/F ST (neutral)] is greater than, smaller than, or equal to 0, respectively (Takahashi et al. 2014b). In addition, population pairwise F ST values for neutral loci should strongly correlate with those for focal loci if stochastic factors (e.g., stochastic drift, secondary contact, and gene flow) predominantly determine the spatial structure of morph frequencies (Runemark et al. 2010; Sánchez-Guillén et al. 2011).
In the Japanese archipelago, a smooth latitudinal cline of female-limited color polymorphism has been observed in the common bluetail, Ischnura senegalensis. Fitness analysis of natural populations of this species has suggested that two antagonistic selection factors, namely, divergent selection and balancing selection, are responsible for the geographic cline of morph frequency. A comparison of the population differentiation of six microsatellite markers and the locus governing color morphs has revealed that the population divergence of color polymorphism in this system is shaped by two antagonistic selective pressures rather than stochastic factors (Takahashi et al. 2014b). Six markers, however, may not be sufficient for inferring population differentiation of neutral loci and consequently population history and demography with a high degree of accuracy. Moreover, although the similarity of morph frequency of two populations should be correlated with environmental similarity rather than geographic proximity if selection–selection balance determines the structure of clinal variation, our previous study did not consider environmental factors such as temperature when estimating the contribution of selection factors, even though morph frequency was correlated with temperature (Takahashi et al. 2014b). The previous work used geographic distance as a proxy of environmental similarity between populations, probably leading to over- or underestimation of the contribution of divergent selection.
In the study reported here, I identified the evolutionary forces responsible for clinal variation of color morph frequency in I. senegalensis using genome-wide single-nucleotide polymorphism (SNP) markers generated by high-throughput next-generation sequencing. Using the SNP marker data, I estimated population structure and then compared the population divergence of putatively neutral loci with that of the putative color locus to infer the contribution of different types of selection (divergent selection and balancing selection) and stochastic factors (gene flow and historical events) under the consideration of environmental distance among populations.
Materials and methods
Study species
Ischnura senegalensis is a common damselfly inhabiting the edges of ponds. Females of this species exhibit genetic color dimorphism (Fig. 1a, b). One of the female morphs is brown (gynomorph) and the other is blue-green (andromorph). Similar to the situation in other damselflies (Johnson 1964, 1966), this color dimorphism is governed by two alleles at a single autosomal locus showing sex-limited expression. The andromorphic allele, A, is expected to be recessive to the gynomorphic allele, G (Takahashi 2011). Polymorphism is maintained by negative frequency-dependent selection derived from positive frequency-dependent male harassment (Takahashi and Watanabe 2010b; Takahashi et al. 2010). Empirical data suggest the occurrence of divergent selection associated with the color of this species induced by gene-by-environment interactions (Takahashi et al. 2011). In the southern portion of the range of I. senegalensis, the relative fitness of andromorphs is lower than that of gynomorphs; the reverse is true in the north.
Morph frequency and population structure
Morph frequencies within populations were estimated during the spring generation by performing a line transect survey along water edges in 2009–2013. Most of the data points overlapped with those of our previous study (Takahashi et al. 2014b), although one additional sampling site in Shiga (35.257°N, 136.216°E) was included. A total of 25 populations were analyzed (Fig. 1c). In each population, color gene allele frequencies and the frequencies of the three genotypes (AA, AG, and GG) were estimated based on phenotypic frequency under the assumptions that the inheritance system of this species matches that reported previously (Takahashi 2011) and that each population was at Hardy–Weinberg equilibrium. To explore the mechanisms shaping the large-scale clinal pattern of morph frequency in the Japanese archipelago, the Hegura and Natori populations analyzed in a previous study (Takahashi et al. 2014b) were excluded due to their unusual characteristics. The former population occurs in ponds with hot springs and the latter population, which is located at the northern limit of the species, is the isolated population in which gynomorphic females are fixed, probably because of a bottleneck.
To estimate the population genetic structure, I used and reanalyzed genome-wide SNP data reported by Takahashi et al. (2016) (doi: 10.5061/dryad.pk30p). The data include 231 SNPs (=loci), which were obtained by multiplexed inter simple sequence repeat (ISSR) genotyping by sequencing (MIG-seq) (Suyama and Matsuki 2015). Most of these SNPs were assumed to be selectively neutral and suitable for inferring population genetic structure generated by neutral processes, such as gene flow and genetic drift.
Population structure estimation and detection of stochastic factors
Genetic population structure based on the MIG-seq loci was assessed using STRUCTURE 2.3.4. The optimal number of genetic clusters of individuals (K value) was determined from the greatest ΔK value, an ad hoc statistic based on the rate of change in the log probability of data between successive K values (Evanno et al. 2005).
I tested for isolation-by-distance patterns based on both neutral and color loci. Geographic distances between populations were calculated as great-circle distances (R package “fields”). Population pairwise F ST values based on the MIG-seq loci were calculated using the program package Arlequin 3.5 (Ecoffier and Lischer 2010). Genotype frequencies at the color locus in each population were estimated based on the phenotypic frequency (see Takahashi et al. 2014b for details) and population pairwise F ST values based on the color locus were also calculated using Arlequin 3.5. As color morph frequencies are expected to be identical (i.e., small pairwise genetic distances based on the color locus) for two populations under similar environmental conditions, I also tested for isolation-by-environment patterns based on neutral and color loci. Because a strong correlation between temperature and morph frequencies of I. senegalensis was previously reported (Takahashi et al. 2014b), pairwise environmental distances between populations were calculated as differences in mean annual temperatures between localities. To examine the relative contribution of stochastic and selection factors on color-locus population structure, I analyzed the correlation between F ST values of MIG loci (F STn) and the color locus (F STc). A strong correlation (i.e., a high correlation coefficient) would suggest that morph frequency in local populations is largely affected by stochastic factors such as genetic drift and historical events, whereas a weak correlation is a signature of the presence of selection (Runemark et al. 2010; Sánchez-Guillén et al. 2011). Relationships between pairwise geographic or environmental distance and genetic distance (F ST) were analyzed by the Mantel test with 10,000 permutations (R package “ade4”).
Detection of selection
As mentioned above, a comparison of population differentiation of neutral loci and loci governing a focal trait can be used to detect the effect of selection and stochastic factors on population divergence (McKay and Latta 2002). Detection of selection factors is difficult, however, when two antagonistic selection factors, such as divergent selection and balancing selection, are simultaneously acting on a given locus. Because divergent selection and balancing selection should respectively increase and decrease population pairwise F ST values for the locus of interest, the presence of selection may be inadvertently overlooked when the effect of one type of selection masks that of the other or the two selection forces counterbalance each other. The selection factors detected by such comparisons will consequently depend on the extent of environmental variation in populations used for the comparison, as the degree of environmental variation determines the relative strength of divergent selection. In this study, I therefore assessed the importance of selection factors as well as genetic drift on population divergence while taking environmental factors into consideration. I examined F STc relative to F STn, that is, R = log10(F STc/F STn), in each of four classes defined according to the differential of mean annual temperature (t) between populations (i.e., 0 ≤ t < 1, 1 ≤ t < 3, 3 ≤ t < 6, and t ≥ 6 °C). The temperature ranges were determined to avoid sample-size bias. Balancing selection and divergent selection were respectively suggested if R was smaller than or greater than 0. Mean annual temperature data for each population were obtained from the Japanese National Land Numerical Information database (http://nlftp.mlit.go.jp/ksj/other/faq.html).
Results
Population genetic structure and contributions of stochastic factors
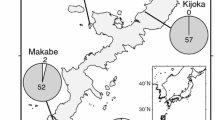
STRUCTURE-based Bayesian clustering identified two genetic clusters of individuals of I. senegalensis in Japan (optimal K = 2) (Fig. 2a). That is, the highest ΔK value was observed for K = 2 and the likelihood value for K = 2 was higher than that for K = 1. Although the estimated cluster membership coefficient (y-axis in Fig. 2a) tended to change with latitude, no clear genetic differentiation among populations was observed. On the other hand, estimated genotype frequencies changed gradually along the length of the Japanese archipelago (Fig. 2b), with a higher andromorph frequency observed in the north. Isolation-by-distance patterns were detected based on the color locus (Mantel test: r = 0.633, P < 0.001), but not putatively neutral loci (MIG loci) (r = 0.196, P = 0.065) (see also Fig. S1). An isolation-by-environment pattern, that is, a correlation between the differential of annual temperature and genetic distance (F ST), was found for the color locus (r = 0.680, P < 0.001), but not for neutral loci (r = 0.271, P = 0.155). Although a significant (r = 0.317, P < 0.009) positive correlation was observed between F STn and F STc, the value of the correlation coefficient was quite low (Fig. 3). Mean F STc (0.24 ± 0.24 [SD]) tended to be larger than mean F STn (0.05 ± 0.01 [SD]). These findings suggest that stochastic factors contribute little to color-locus population divergence.
Estimated population structure based on neutral loci estimated by Bayesian structure analyses using the program STRUCTURE (a) and the putative color locus (b) of Ischnura senegalensis. a Individuals are represented by thin vertical lines in the bar graph in the inset, which are partitioned into K (=2) segments representing each individual’s estimated membership fraction. b Genotype frequencies in each population (pie chart) were calculated from phenotype frequencies. Numbers above the bar plot and in the pie chart indicate the numbers of individuals used for population genetic analysis and those used to estimate color morph frequency for each population
Contribution of selection factors
Diversification of the color locus relative to neutral loci (i.e., log10[F STc/F STn]) tended to increase with environmental distance (Fig. 4). On the one hand, the relative diversification of the color locus was less than 0 between populations having an annual temperature difference of less than 1 °C, which suggests the presence of balancing selection acting on the color locus. On the other hand, the relative diversification of the color locus was greater than 0 between populations having an annual temperature difference greater than 1 °C. This suggests that differences in the color locus among populations under different environmental conditions are predominantly due to divergent rather than balancing selection.
Diversification of the color locus relative to neutral loci as a function of environmental distance (t) between populations (0 ≤ t < 1, 1 ≤ t < 3, 3 ≤ t < 6, and t ≥ 6 °C). Mean log10(F STc/F STn) was negative in population pairs separated by a small environmental distance (0–1 °C apart) and positive in all other population pairs. The numbers beside each plot indicate sample size (the number of pairwise comparisons) in each category
Discussion
In this study, I have demonstrated the contribution of both balancing and divergent selection to the geographic structure of female color morphs of I. senegalensis. I found no definitive evidence of any effects of stochastic factors or historical events that can explain the geographic pattern of female color morphs. These patterns are qualitatively the same as those uncovered in a previous study that used several microsatellite loci (Takahashi et al. 2014b). My high-resolution analysis using genome-wide SNPs with consideration of environmental distance among populations has confirmed that the geographic cline of female morph frequency in I. senegalensis is due to a combination of two antagonistic selection factors rather than stochastic events.
When two historically allopatric populations with different alleles come into secondary contact, subsequent admixture can transiently generate a spatial cline of morph frequency, even though such a cline is not maintained on an evolutionary time scale. Alternatively, a spatial cline of morph/allele frequency can be established by a combination of two processes: divergent selection generating spatial differentiation in morph frequencies, and admixture among populations leading to the coexistence of multiple morphs within a single population, that is, migration–selection balance (Endler 1977). Nevertheless, I found that a combination of balancing selection and divergent selection can largely explain the large-scale geographic pattern of color polymorphism in I. senegalensis, a finding expected from a previous analysis of the fitness of natural populations (Takahashi et al. 2010, 2014b). Balancing selection, which can maintain polymorphisms in each population, is indeed suggested to contribute to the establishment of a large-scale cline of morph frequency (Endler 1973). Because I. senegalensis is sedentary, similar to other coenagrionid damselflies (Allen and Thompson 2010), the idea that migration contributes relatively little to the establishment of a smooth cline in I. senegalensis morph frequency is plausible, even though the contribution of stochastic factors has been suggested in some other damselflies (Iserbyt et al. 2010; Sánchez-Guillén et al. 2011).
I found that both divergent and balancing selection act on a color locus by taking into account the environmental (temperature) distance between populations. If environmental (temperature) distance were not considered, I would not detect both divergent and balancing selection simultaneously by comparing neutral and target loci. For instance, for my dataset, balancing selection would not be detected because the effect of divergent selection on population divergence masks the relatively small contribution of balancing selection at a large geographic scale. Likewise, if populations only extend over small spatial scales with small environmental variation, divergent selection would hardly be detected. In fact, recent genetic analyses on polymorphic damselflies did not consider environmental distance among populations, and thus detected only one of the two selective factors (Andrés et al. 2000; Wong et al. 2003; Abbott et al. 2008; Sánchez-Guillén et al. 2011; Inomata et al. 2015). In damselfly, female morph frequency is known to change with latitude (Gosden et al. 2011; Takahashi et al. 2011) and altitude (Cooper 2010). These findings suggest that temperature differentially affects the fitness of each female morph and determines the equilibrium frequency of female morphs in each population, generating a morph frequency cline along the temperature gradient. Takahashi et al. (2014b) have considered geographic distance among populations when detecting selection, but geographic distance is just a proxy of environmental (temperature) distance, possibly leading to the failure to detect selective factors due to scaling error. I actually found that environmental distance well explained population pairwise F STc compared with geographic distance. In the present study, I detected both divergent and balancing selection by considering environmental (temperature) distance between populations and found that environmental distance explains the relative strength of divergent selection acting on a color locus. The scaling of populations for comparison by using environmental distance may be reasonable, especially when populations have wide distributions both latitudinally and longitudinally.
Given that the geographic pattern of the color locus happens to be similar to that of neutral loci, I cannot detect the signatures of any selective forces shaping this pattern. In my study system, isolation-by-distance patterns were found for only color locus and thus successfully detected the deviation of F STc from F STn. This means that the accurate detection of selection forces may more or less depend upon the genetic population structure estimated by using neutral genetic markers. Although no isolation-by-distance pattern was found by using six microsatellite loci (Takahashi et al. 2014b), the current genome-wide population genetic analysis detected a relatively clear isolation-by-distance pattern (see Fig. S1). The improvement of the estimation of population structure by next-generation sequencing must have contributed to the accurate detection of selection, as well as the consideration of environmental distance.
In this study, I estimated allele/genotype frequencies for the color locus on the basis of phenotype frequency while assuming that each population was at Hardy–Weinberg equilibrium (Takahashi and Watanabe 2010a) and that the previously reported inheritance patterns were accurate (Takahashi 2011). Although these assumptions are reasonable, the direct use of the specific gene(s) responsible for color morphs would improve the accuracy of allele/genotype frequency estimation and the detection of selection and stochastic factors acting on the gene(s), since unknown genetic factors can potentially affect female body color and segregation ratio (Sanmartín-Villar and Cordero-Rivera 2016). Because the color gene is autosomal, the availability of male genotype data would facilitate the estimation of population allele/genotype frequencies. Identification and application of the color gene should facilitate a highly accurate analysis of selection acting on this locus. Finally, a comparison of gene sequences among individuals may allow the signatures of selection forces acting on the color locus to be detected (Nielsen et al. 2007).
References
Abbott JK, Bensch S, Gosden TP, Svensson EI (2008) Patterns of differentiation in a colour polymorphism and in neutral markers reveal rapid genetic changes in natural damselfly populations. Mol Ecol 17:1597–1604. doi:10.1111/j.1365-294X.2007.03641.x
Allen KA, Thompson D (2010) Movement characteristics of the Scarce Blue-tailed Damselfly, Ischnura pumilio. Insect Cons Diver 3:5–14
Andrés JA, Sánchez-Guillén RA, Cordero-Rivera A (2000) Molecular evidence for selection on female color polymorphism in the damselfly Ischnura graellsii. Evolution 54:2156–2161
Brakefield PM, de Jong PW (2011) A steep cline in ladybird melanism has decayed over 25 years: a genetic response to climate change. Heredity 107:574–578. doi:10.1038/hdy.2011.49
Cheviron ZA, Brumfield RT (2009) Migration-selection balance and local adaptation of mitochondrial haplotypes in rufous-collared sparrows (Zonotrichia capensis) along an elevational gradient. Evolution 63:1593–1605. doi:10.1111/j.1558-5646.2009.00644.x
Cook LM, Saccheri IJ (2012) The peppered moth and industrial melanism: evolution of a natural selection case study. Heredity 110:207–212. doi:10.1038/hdy.2012.92
Cook LM, Mani GS, Varley ME (1986) Postindustrial melanism in the peppered moth. Science 231:611–613. doi:10.1126/science.231.4738.611
Cooper IA (2010) Ecology of sexual dimorphism and clinal variation of coloration in a damselfly. Am Nat 176:566–572. doi:10.1086/656491
Ecoffier L, Lischer HEL (2010) Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour 10:564–567. doi:10.1111/j.1755-0998.2010.02847.x
Endler JA (1973) Gene flow and population differentiation. Science 179:243–250
Endler JA (1977) Geographic variation, speciation, and clines. Princeton University Press, New Jersey
Evanno G, Regnaut S, Goudet J (2005) Detecting the number of clusters of individuals using the software structure: a simulation study. Mol Ecol 14:2611–2620. doi:10.1111/j.1365-294X.2005.02553.x
Forsman A, Ahnesjo J, Caesar S, Karlsson M (2008) A model of ecological and evolutionary consequences of color polymorphism. Ecology 89:34–40
Gillespie RG, Oxford GS (1998) Selection on the color polymorphism in hawaiian happy-face spiders: evidence from genetic structure and temporal fluctuations. Evolution 52:775–783
Gosden TP, Stoks R, Svensson EI (2011) Range limits, large-scale biogeographic variation, and localized evolutionary dynamics in a polymorphic damselfly. Biol J Linn Soc 102:775–785. doi:10.1111/j.1095-8312.2011.01619.x
Hammers M, Van Gossum H (2008) Variation in female morph frequencies and mating frequencies: random, frequency-dependent harassment or male mimicry? Anim Behav 76:1403–1410. doi:10.1016/j.anbehav.2008.06.021
Hodgins KA, Barrett SCH (2008) Asymmetrical mating patterns and the evolution of biased style-morph ratios in a tristylous daffodil. Genet Res 90:3–15. doi:10.1017/S0016672307008956
Inomata N, Hironaka K, Sawada K et al (2015) Discrepancy in the degree of population differentiation between color-morph frequencies and neutral genetic loci in the damselfly Ischnura senegalensis in Okinawa Island, Japan. Genetica 143:1–7. doi:10.1007/s10709-015-9821-x
Iserbyt A, Bots J, Van Gossum H, Jordaens K (2010) Did historical events shape current geographic variation in morph frequencies of a polymorphic damselfly? J Zool 282:256–265
Itoh S (1991) Geographical variation of the plumage polymorphism in the Eastern Reef heron (Egretta sacra). Condor 93:383–389
Johnson C (1964) The inheritance of female dimorphism in the damselfly, Ischnura damula. Genetics 49:513–519
Johnson C (1966) Genetics of female dimorphism in Ischnura demorsa. Heredity 21:453–459
Kazancıoğlu E, Arnqvist G (2013) The maintenance of mitochondrial genetic variation by negative frequency-dependent selection. Ecol Lett 17:22–27. doi:10.1111/ele.12195
Komai T, Chino M, Hoshino Y (1950) Contributions to the evolutionary genetics of the lady-beetle, Harmonia. I. geographic and temporal variations in the relative frequencies of the elytral pattern types and in the frequency of elytral ridge. Genetics 35:589–601
Latta RG, Mitton JB (1999) Historical separation and present gene flow through a zone of secondary contact in ponderosa pine. Evolution 769–776
Mallet J, Barton N (1989) Inference from clines stabilized by frequency-dependent selection. Genetics 122:967–976
McKay JK, Latta RG (2002) Adaptive population divergence: markers, QTL and traits. Trends Ecol Evol 17:285–291
Nielsen R, Hellmann I, Hubisz M et al (2007) Recent and ongoing selection in the human genome. Nat Rev Genet 8:857–868. doi:10.1038/nrg2187
Runemark A, Hansson B, Pafilis P et al (2010) Island biology and morphological divergence of the Skyros wall lizard Podarcis gaigeae: a combined role for local selection and genetic drift on color morph frequency divergence? BMC Evol Biol 10:269. doi:10.1186/1471-2148-10-269
Saccheri IJ, Rousset F, Watts PC et al (2008) Selection and gene flow on a diminishing cline of melanic peppered moths. Proc Natl Acad Sci 105:16212–16217. doi:10.1073/pnas.0803785105
Sánchez-Guillén RA, Hansson B, Wellenreuther M et al (2011) The influence of stochastic and selective forces in the population divergence of female colour polymorphism in damselflies of the genus Ischnura. Heredity 107:513–522. doi:10.1038/hdy.2011.36
Sanmartín-Villar I, Cordero-Rivera A (2016) The inheritance of female colour polymorphism in Ischnura genei (Zygoptera: Coenagrionidae), with observations on melanism under laboratory conditions. PeerJ 4:e2380–19. doi:10.7717/peerj.2380
Schemske DW, Bierzychudek P (2007) Spatial differentiation for flower color in the desert annual Linanthus parryae: was Wright right? Evolution 61:2528–2543. doi:10.1111/j.1558-5646.2007.00219.x
Slatkin M (1973) Gene flow and selection in a cline. Genetics 75:733–756
Suyama M, Matsuki Y (2015) MIG-seq: an effective PCR-based method for genome-wide single-nucleotide polymorphism genotyping using the next-generation sequencing platform. Sci Rep 5:16963. doi:10.1038/srep16963
Takahashi Y (2011) Testing negative frequency-dependent selection: linking behavioral plasticity and evolutionary dynamics. Bull Kanto Branch Ecol Soc Jpn 59:8–14
Takahashi Y, Watanabe M (2010a) Mating experience affecting male discrimination between sexes and female morphs in Ischnura senegaleasis (rambur) (zygoptera: coenagrionidae). Odonatologica 39:47–56
Takahashi Y, Watanabe M (2010b) Female reproductive success is affected by selective male harassment in the damselfly Ischnura senegalensis. Anim Behav 79:211–216. doi:10.1016/j.anbehav.2009.10.032
Takahashi Y, Yoshimura J, Morita S, Watanabe M (2010) Negative frequency-dependent selection in female color polymorphism of a damselfly. Evolution 64:3620–3628. doi:10.1111/j.1558-5646.2010.01083.x
Takahashi Y, Morita S, Yoshimura J, Watanabe M (2011) A geographic cline induced by negative frequency-dependent selection. BMC Evol Biol 11:256. doi:10.1186/1471-2148-11-256
Takahashi Y, Kagawa K, Svensson EI, Kawata M (2014a) Evolution of increased phenotypic diversity enhances population performance by reducing sexual harassment in damselflies. Nat Com 5:1–7. doi:10.1038/ncomms5468
Takahashi Y, Nagata N, Kawata M (2014b) Antagonistic selection factors induce a continuous population divergence in a polymorphism. Heredity 112:391–398. doi:10.1038/hdy.2013.117
Takahashi Y, Suyama Y, Matsuki Y, Funayama R, Nakayama K, Kawata M (2016) Lack of genetic variation prevents adaptation at the geographic range margin in a damselfly. Mol Ecol 25:4450–4460. doi:10.1111/mec.13782
Wennersten L, Forsman A (2009) Does colour polymorphism enhance survival of prey populations? Proc R Soc B 276:2187–2194. doi:10.1098/rspb.2009.0252
Wennersten L, Forsman A (2012) Population-level consequences of polymorphism, plasticity and randomized phenotype switching: a review of predictions. Biol Rev 87:756–767. doi:10.1111/j.1469-185X.2012.00231.x
Whibley AC, Langlada NB, Andalo C et al (2006) Evolutionary paths underlying flower color variation in Antirrhinum. Science 313:963–966. doi:10.1126/science.1129161
Wong A, Smith ML, Forbes MR (2003) Differentiation between subpopulations of a polychromatic damselfly with respect to morph frequencies, but not neutral genetic markers. Mol Ecol 12:3505–3513. doi:10.1046/j.1365-294X.2003.02002.x
Wright S (1943) Isolation by distance. Genetics 28:114–138
Acknowledgements
The author thanks Yoshihisa Suyama, Yu Matsuki, Ryo Funayama, Keiko Nakayama, and Masakado Kawata for generating the original SNP data analyzed in this study. Yukari Suzuki-Ohno provided the dataset on temperature at each locality. This work was partly supported by the Japan Society for the Promotion of Science (KAKENHI grant no. 25891004).
Author information
Authors and Affiliations
Corresponding author
Additional information
Yuma Takahashi is the recipient of the 19th Denzaburo Miyadi Award.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Takahashi, Y. Genome-wide population genetic analysis identifies evolutionary forces establishing continuous population divergence. Ecol Res 32, 461–468 (2017). https://doi.org/10.1007/s11284-017-1459-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11284-017-1459-y