RoleSim*: Scaling axiomatic role-based similarity ranking on large graphs

Abstract

RoleSim and SimRank are among the popular graph-theoretic similarity measures with many applications in, e.g., web search, collaborative filtering, and sociometry. While RoleSim addresses the automorphic (role) equivalence of pairwise similarity which SimRank lacks, it ignores the neighboring similarity information out of the automorphically equivalent set. Consequently, two pairs of nodes, which are not automorphically equivalent by nature, cannot be well distinguished by RoleSim if the averages of their neighboring similarities over the automorphically equivalent set are the same. To alleviate this problem: 1) We propose a novel similarity model, namely RoleSim*, which accurately evaluates pairwise role similarities in a more comprehensive manner. RoleSim* not only guarantees the automorphic equivalence that SimRank lacks, but also takes into account the neighboring similarity information outside the automorphically equivalent sets that are overlooked by RoleSim. 2) We prove the existence and uniqueness of the RoleSim* solution, and show its three axiomatic properties (i.e., symmetry, boundedness, and non-increasing monotonicity). 3) We provide a concise bound for iteratively computing RoleSim* formula, and estimate the number of iterations required to attain a desired accuracy. 4) We induce a distance metric based on RoleSim* similarity, and show that the RoleSim* metric fulfills the triangular inequality, which implies the sum-transitivity of its similarity scores. 5) We present a threshold-based RoleSim* model that reduces the computational time further with provable accuracy guarantee. 6) We propose a single-source RoleSim* model, which scales well for sizable graphs. 7) We also devise methods to scale RoleSim* based search by incorporating its triangular inequality property with partitioning techniques. Our experimental results on real datasets demonstrate that RoleSim* achieves higher accuracy than its competitors while scaling well on sizable graphs with billions of edges.

1 Introduction

RoleSim, conceived by Jin et al. [9], is a promising role-oriented graph-theoretic measure that quantifies the similarity between two objects based on graph automorphism, with a proliferation of real-life applications [9, 10, 25], such as link prediction (social network), co-citation analysis (bibliometrics), motif discovery (bioinformatics), and collaborative filtering (information retrieval). It recursively follows a SimRank-like reasoning that “two nodes are assessed as role similar if they interact with automorphically equivalent sets of in-neighbors”. Intuitively, automorphically equivalent nodes in a graph are objects having similar roles that can be exchanged with minimum effect on the graph structure. Similar to the well-known SimRank measure [7], the recursive nature of RoleSim allows to capture the multi-hop neighboring structures that are automorphically equivalent in a network. Unlike SimRank that measures the similarity of two nodes from the paths connecting them, RoleSim quantifies similarities through the paths connecting their different roles. As a result, two nodes that are disconnected from each other will not be considered as dissimilar by RoleSim if they have similar roles. For evaluating similarity score s(a,b) between nodes a and b, as opposed to SimRank whose similarity s(a,b) takes the average similarity of all the neighboring pairs of (a,b), RoleSim computes s(a,b) by averaging only the similarities over the maximum bipartite matching of all the neighboring pairs of (a,b). This subtle difference enables RoleSim to guarantee the automorphic equivalence, which SimRank lacks, in final scoring results. Therefore, RoleSim has been demonstrated as an effective similarity measure in a wide range of real applications. We summarize two of these applications below.

Application 1 (Similarity Search on the Web)

Discovering web pages similar to a query page is an important task in information retrieval. In a Web graph, each node represents a web page, and an edge denotes a hyperlink from one page to another. RoleSim can be applied to measure the similarity of two web pages, based on the intuition that “two web pages are role-similar if they are pointed to by the automorphically equivalent sets of their in-neighboring pages”. This similarity measure produces more reliable similarity results than the SimRank model [10].

Application 2 (Social Network De-anonymization)

Social network de-anonymization is a method to validate the strength of anonymization algorithms that protect a user’s privacy. RoleSim has been applied to de-anonymise node mappings based on the similarity information between a crawled network and an anonymised one. Based on the observation that “correct mappings tend to have higher similarity scores”, RoleSim iteratively evaluates pairwise node similarities between two networks, and captures the reasoning that “a pair of nodes between two networks is more likely to be a correct mapping if their neighbors are correct mappings”. RoleSim has demonstrated superior performance as compared with other existing de-anonymization algorithms [25].

Despite its popularity in real-world applications, RoleSim has a major limitation: with the aim to achieve automorphic equivalence, its similarity score s(a,b) only considers the limited information of the average similarity scores over the automorphically equivalent set (i.e., the maximum bipartite matching) of a’s and b’s in-neighboring pairs, but neglects the rest of the pairwise in-neighboring similarity information that is outside the automorphically equivalent set. Consequently, RoleSim does not always produce comprehensive similarity results because two pairs of nodes, which are not automorphically equivalent by nature, should be distinguishable from each other even though the average values of their in-neighboring similarities over the set of the maximum bipartite matching are the same, as illustrated in Example 1.

Example 1 (Limitation of RoleSim)

Consider the web graph G in Figure 1, where each node denotes a web page, and each edge depicts a hyperlink from one page to another. Using RoleSim, we evaluate pairs of similarities between nodes, as partially illustrated in the ‘RS’ column of the right table. It is discerned that node-pairs (1,2) and (1,3) have the same RoleSim similarity values, which is not reasonable. Because node 2 and node 3 are not strictly automorphically equivalent by nature, their similarities with respect to the same query node 1, i.e.,s(1,2) and s(1,3), should not be the same.

Fig. 1

Limitation of RoleSim (RS) on a web graph, where node-pairs (1,2) and (1,3) have the same RoleSim score (0.426) since RS aggregates only the in-neighboring pairs that are automorphically equivalent (colored in green) whose sums are the same (0.488 + 0.360 = 0.848), while ignoring the remaining pairs

We notice that the main reason why s(1,2) and s(1,3) are assessed to be the same by the RoleSim model is that its similarity s(a,b) considers only the average similarity scores over the maximum bipartite matching, denoted as M_a,b, of (a,b)’s in-neighboring pairs I_a × I_b, where I_a denotes the in-neighbor set of node a, and × is the Cartesian product of two sets. Thus, the similarity information in the remaining in-neighboring pairs of (a,b), i.e., I_a × I_b − M_a,b, are totally ignored. For example, if unfolding the in-neighboring pairs of (1,2) and (1,3) respectively, we see that, in the gray cells, M_1,2 = {(4,6),(5,7)} (resp.M_1,3 = {(4,9),(5,10)}) is the maximum bipartite matching of (1,2)’s (resp. (1,3)’s) in-neighboring pairs I₁ × I₂ (resp.I₁ × I₃). The sum of the similarity values over M_1,2 is 0.488 + 0.360 = 0.848, which is the same as that over M_1,3. Thus, RoleSim cannot distinguish s(1,2) from s(1,3).

Example 1 illustrates that, to effectively evaluate s(a,b), relying only on the in-neighboring-pairs similarities in the maximum bipartite matching M_a,b (e.g., RoleSim) is not enough. Although RoleSim has the advantage of using intuitively the most influential pairs M_a,b among all the in-neighboring pairs I_a × I_b for achieving automorphic equivalence, it completely ignores the similarity information outside M_a,b. For instance in Example 1, there are opportunities to take good advantage of the similarity values in the regions I₁ × I₂ − M_1,2 and I₁ × I₃ − M_1,3 which would be helpful to distinguish s(1,2) from s(1,3) further when the average similarities over M_1,2 and M_1,3 are the same.

Contributions

Motivated by this, our main contributions are as follows:

• 1) We first propose a novel similarity model, RoleSim*, which accurately evaluates pairwise role similarities in a more comprehensive fashion. Compared with the existing well-known similarity models (e.g., SimRank and RoleSim), RoleSim* not only guarantees the automorphic equivalence that SimRank lacks, but also takes into consideration the pairwise similarities outside the automorphically equivalent sets that are overlooked by RoleSim. (Section 3.1)

• 2) We show three key properties of RoleSim*, i.e., symmetry, boundedness, and non-increasing monotonicity of its iterative similarity scores. On the top of that, we prove the existence and uniqueness of the RoleSim* solution. (Section 3.2)

• 3) We derive an iterative formula for computing RoleSim* similarities. A concise upper bound for RoleSim* iterations is also established, which can estimate the total number of iterations required for attaining a desired accuracy. (Section 3.3)

• 4) To substantially accelerate the computation of RoleSim*, we also devise a threshold-based RoleSim* model based on two pruning strategies, and provide provable guarantees on accuracy which is controlled by a user-specified threshold parameter δ trading between speed and accuracy. (Section 4)

• 5) To scale RoleSim* similarity search well on large graphs with billions of edges, we propose a scalable algorithm for single-source RoleSim* retrieval, which avoids spending unnecessary time on repeated RoleSim* computations while caching important pairs through an unordered hash map. (Section 5)

• 6) We induce a distance metric based on our RoleSim* measure, and rigorously show that the RoleSim* distance metric fulfills the triangular inequality which other measures (e.g., cosine distance) lack. This implies the sum-transitivity of the RoleSim* measure. (Section 6)

• 7) We discuss approaches to scale RoleSim* based search using the triangle inequality property and partitioning techniques (Section 7).

• 8) We conduct an experimental study to validate the effectiveness of our RoleSim* model. Our empirical results show that RoleSim* achieves higher accuracy than the existing competitors (e.g., RoleSim and SimRank) while entailing comparable computational complexity bounds of RoleSim. We also devise an unsupervised experimental setting that quantifies the effectiveness of similarity measures, where RoleSim* outperforms the alternatives. (Section 8)

2 Related work

Graph-based similarity models have been popular since SimRank measure was proposed by Jeh and Widom [7]. SimRank is a node-pair similarity measure, which follows the recursive idea that “two nodes are considered as similar if they are pointed to by similar nodes”. Since then, there have been surges of studies focusing on optimization problems to accelerate SimRank computation as the naive SimRank computing method entails quadratic time in the number of nodes. According to assumptions on data updates, recent results can be divided into static algorithms [1, 4, 5, 12, 16, 22, 26, 32, 34, 37, 42], and dynamic algorithms on evolving graphs [8, 13, 19, 24, 28, 36, 40]. According to types of queries, these results are classified into single-source SimRank [8, 12, 19, 26, 40], single-pair SimRank [6, 15], all-pairs SimRank [1, 20, 34, 35], and partial-pairs SimRank [22, 39].

Recent years have witnessed an upsurge of interest in the semantic problems of pairwise similarity measures. Various SimRank and SimRank-like models have come into play. Representative examples include C-Rank [31], SimFusion [38], Penetrating-Rank [41], RoleSim++ [25], RoleSim [9], MatchSim [18], SimRank* [37], ASCOS [3], CoSimRank [23], and SemSim [32]. In what follows, we will elaborate the pros and cons of these similarity measures and discuss their relations to this work.

C-Rank [31]

C-Rank is a contribution-based ranking algorithm that integrates both content and link information of web pages through the concept of contribution, indicating that a page may contribute to enhancing the content quality of adjacent pages pointing to it via linkages. A C-Rank score of each page on a term is defined to be a linear combination of (i) its relevance score to the term and (ii) its contribution score that quantifies the degree of its overall contributions to other pages on the term. However, unlike similarity scores from the RoleSim family, C-Rank does not take into account the automorphic equivalence property for each pair of nodes. Our experimental evaluation demonstrates the accuracy of RoleSim* is superior to C-Rank with a little compromise in the computational time.

Penetrating-Rank [41]

Zhao et al. [41] proposed Penetrating-Rank, which is a SimRank-based similarity measure that comprehensively considers both incoming and outgoing neighbouring information for similarity assessment. However, Penetrating-Rank is not an automorphic equivalence-based measure as role discovery is not the primary task of this model. Recently, the idea of Penetrating-Rank applied to SimRank shows some degree of resemblance to the idea of RoleSim++, which is a generalisation of RoleSim through exploitation of both in- and out-links of the graph structure.

RoleSim [10]

RoleSim has been accepted as a promising role-based similarity model, due to its elegant intuition that “if two nodes are automorphically equivalent, they should share the same role and their role similarity should be maximal”. To speed up the RoleSim computation, an approximate heuristic, named Iceberg RoleSim, was devised to prune small similarity values below a threshold. Unlike SimRank that takes the average similarity of all the neighboring pairs of (a,b), RoleSim computes s(a,b) by averaging only the similarities over the maximum bipartite matching M_a,b. However, all the similarity information not included in the matching M_a,b is completely ignored by RoleSim. In contrast, our RoleSim* model can effectively capture these information while guaranteeing automorphic equivalence.

RoleSim++ [25]

RoleSim++, proposed by Shao et al. [25], takes good advantage of the direction information of both in- and out-links to model pairwise similarities. which is successfully used in the real-world de-anonymization application. It employs a novel matching algorithm, NeighborMatch, to find matchings for inner and outer neighbors, respectively. Moreover, a threshold-based model, α-RoleSim++, is proposed to eliminate tiny scores for speedup further. Our techniques of RoleSim* can also be slightly modified to tailor RoleSim++ to accommodate similarity contributions from non-automorphically equivalent pairs of in- and out-neighbours for semantic enhancement.

SimFusion [30]

SimFusion exploits a unified relationship matrix (URM) to capture the inter- and intra-relationships among a set of heterogeneous data objects. A unified similarity matrix (USM), which is evaluated iteratively from the URM, characterises the latent relationships among heterogeneous data objects. However, as opposed to RoleSim*, SimFusion fails to capture automorphically equivalent relationships among the heterogeneous data objects.

MatchSim [18]

Lin et al. [18] introduced MatchSim similarity model, which computes the similarity values between two objects based on the average similarity of their maximum matched neighbours. The key difference between MatchSim and RoleSim lies in the initialisation step – MatchSim starts with an identity matrix as its initial similarity and defines s₀(a,b) = 1 if a = b, and 0 otherwise, whereas RoleSim utilises a matrix of all ones to be starting similarity matrix which initialises all s₀(∗,∗) = 1. As a result, RoleSim exhibits the automorphism property that MatchSim lacks. However, similar to RoleSim, MatchSim totally neglects the neighboring similarity values outside the automorphically equivalent sets. The idea of RoleSim* can be applied to MatchSim in a similar way to resolve this problem.

SimRank* [37] & ASCOS [3]

SimRank* and ASCOS are two variations of the SimRank model that addresses the zero-similarity problem of the SimRank measure. Nevertheless, these methods do not take into account the automorphically equivalent structure of nodes. The key idea of RoleSim* can be applied in a similar manner to SimRank* and ASCOS models to enrich the meaningful semantics of similarity assessment while effectively circumventing the zero SimRank problem.

CentSim [14]

Li et al. [14] proposed CentSim, a centrality-based role similarity measure, which compares the centrality values of two nodes to evaluate their similarity. This measure employs several types of centrality including PageRank, Degree and Closeness for each node, and considers the weighted average of them for evaluating CentSim scores.

SemSim [32]

Milo et al. [32] proposed a semantic-aware random walk-based model namely, SemSim, which is an extension of SimRank applied to heterogeneous information networks. SemSim aims to boost the quality of SimRank similarity scores by exploiting its node semantics and edge weights. Nonetheless, SemSim inherits the limitation of SimRank whose similarity values ignore the role-equivalent relationship between nodes.

Co-SimRank [23]

Rothe and Schütze [23] presented Co-SimRank, a SimRank-like measure of pairwise similarity based on graph structure. A Co-SimRank score s(a,b) of each pair (a,b) is computed from the inner product of two Personalised PageRank vectors corresponding to the seed node a and b, respectively. Co-SimRank distinguishes from SimRank in that the SimRank value s(a,b) counts only the first hitting time of two random surfers starting at nodes a and b, whereas CoSimRank values tallies all the hitting times of the two random surfers. As a result, CoSimRank produces more complete similarity scores than SimRank. In comparison to RoleSim*, the values of CoSimRank do not look at the automorphically equivalent patterns of the graph. However, the intuition of RoleSim* can be extended to Co-SimRank for semantic enhancement.

SimRank

There have also been a variety of studies on SimRank algorithms recently (e.g., [8, 21, 24, 27, 29]). Wang et al. [27] presents a fast probabilistic Monte-Carlo algorithm, ExactSim, to evaluate single-source and top-k SimRank results on large-scale graphs with over 10⁶ nodes effectively. ExactSim provides high-probability guarantees to yield ground truths with provable accuracy. Lu et al. [21] proposed a matrix sampling approach in combination with the steepest descent technique, which not only guarantees the sparsity of the involved matrix, but also speeds up the rate of convergence for a single-pair SimRank retrieval. Wei et al. [29] proposes PRSim, which resorts to the distribution of the reverse PageRank to accelerate single-source SimRank queries, achieving sublinear query time on power-law graphs with small index size. READS [8] precalculates $\sqrt {c}$-walks and squeezes random walks into compact trees. In the query processing, READS searches the walks commencing at the query node u, and retrieves all the $\sqrt {c}$-random walks which hit the $\sqrt {c}$-walks of u. TSF [24] constructs one-way graphs for indexing through sampling an in-neighbour from the in-links of each node. In the query processing, the one-way graphs are utilised to retrieve random walks for SimRank evaluation.

3 RoleSim*

3.1 RoleSim* formulation

The central intuition underpinning RoleSim* follows a recursive concept that two distinct nodes are assessed to be similar if they

• 1. interact with the automorphically equivalent sets of in-neighbors, and

• 2. are in-linked by similar nodes out of automorphically equivalent sets.

The starting point for this recursion is to assign each pair of nodes a similarity score 1, meaning that initially no pairs of nodes are thought of to be more (or less) similar than others.

Notations

Before illustrating the mathematical definition to reify the RoleSim* intuition, we introduce the following notations.

Let G = (V,E) be a directed graph with a set of nodes V and a set of edges E. Let I_a be all in-neighbors of node a, and |I_a| the cardinality of the set I_a. For a pair of nodes (a,b) in G, we denote by I_a × I_b = {(x,y) | x ∈ I_a and y ∈ I_b} all in-neighboring pairs of (a,b), and s(a,b) the RoleSim* similarity score between nodes a and b. Using I_a × I_b and s(a,b), we define a weighted complete bipartite graph, denoted by ${\mathcal K}_{|I_{a}|, |I_{b}|}= (I_{a} \cup I_{b}, I_{a} \times I_{b})$, with each edge (x,y) ∈ I_a × I_b carrying the weight s(a,b). We denote by $M_{a,b} \ (\subseteq I_{a} \times I_{b})$ the maximum weighted matching in bipartite graph ${\mathcal K}_{|I_{a}|, |I_{b}|}$.

Example 2

Recall graph G in Figure 1. For nodes 1 and 2, their in-neighbors are sets I₁ = {4,5} and I₂ = {6,7,8}, respectively. The set of all in-neighboring pairs of (1,2) is I₁ × I₂ = {(4,6),(4,7),(4,8),(5,6),(5,7),(5,8)}. The maximum matching of bipartite graph (I₁ ∪ I₂,I₁ × I₂) is M_1,2 = {(4,6),(5,7)} (see the pairs in bold font in I₁ × I₂).

Other notations frequently used throughout this paper are listed in Table 1.

Table 1 Description of main symbols

RoleSim* Formula.

Based on our aforementioned intuition, we formally formulate the RoleSim* model as follows:

$$ \begin{array}{@{}rcl@{}} s(a,b) =\beta \bigg(\lambda & \times& \overbrace{\frac{1 }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{s}(x,y)}^{{\textrm{Part 1: average similarity over maximum matching $M_{a,b}$}}} \\ +(1-\lambda ) & \times &\underbrace{\frac{1}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{s}(x,y)}_{{\textrm{Part 2: average similarity over $(I_{a} \times I_{b})-M_{a,b}$}}} \bigg)+(1-\beta ) \end{array} $$

(1)

In (1), for every pair of nodes (a,b), the set of their in-neighboring pairs, I_a × I_b, is split into two subsets: I_a × I_b = M_a,b ∪ (I_a × I_b − M_a,b). As a result, the definition of RoleSim* consists of two parts: Part 1 is the average similarity over maximum matching M_a,b, indicating the contribution from (a,b) interacting with the automorphically equivalent set, M_a,b, of (a,b)’s in-neighbors pairs. Part 2 is the average similarity over (I_a × I_b) − M_a,b, corresponding to the contribution from (a,b) being pointed to by the rest of (a,b)’s in-neighbors pairs out of automorphically equivalent set M_a,b.

It is worth highlighting that the reason why we use the denominator $\left | {{I}_{a}} \right |+\left | {{I}_{b}} \right |-\left | {{M}_{a,b}} \right |$ instead of $\left | {{M}_{a,b}} \right |$ in (1) is to guarantee that RoleSim* covers the traditional RoleSim model as a special case when λ = 1. More specifically, since $\left | {{M}_{a,b}} \right |={\min \limits } \{\left | {{I}_{a}} \right |,\left | {{I}_{b}} \right |\}$, it follows that $\left | {{I}_{a}} \right |+\left | {{I}_{b}} \right |-\left | {{M}_{a,b}} \right |={\max \limits } \{\left | {{I}_{a}} \right |,\left | {{I}_{b}} \right |\}$. When we apply this to (1) and set λ = 1, Part 2 of (1) becomes zero, and (1) reduces to the following traditional RoleSim equation:

$$ s(a,b)=\frac{\beta }{\max \{\left| {{I}_{a}} \right|,\left| {{I}_{b}} \right|\}}\sum\limits_{(x,y)\in {{M}_{a,b}}}{s(x,y)}+(1-\beta ) $$

(2)

The reason why RoleSim in (2) uses ${\max \limits } \{\left | {{I}_{a}} \right |,\left | {{I}_{b}} \right |\} \ \left (= \left | {{I}_{a}} \right |+\left | {{I}_{b}} \right |-\left | {{M}_{a,b}} \right | \right )$ as the denominator instead of $\left | {{M}_{a,b}} \right |\ \left (={\min \limits } \{\left | {{I}_{a}} \right |,\left | {{I}_{b}} \right |\} \right )$ is to differentiate similarity values of the pairs s(a,b) and s(a,c) when $\left | {{I}_{b}} \right |\ne \left | {{I}_{c}} \right |$. The larger the difference between $\left | {{I}_{b}} \right |$ and $\left | {{I}_{c}} \right |$, the more dissimilar the similarity values of s(a,b) and s(a,c) should be. For example, recall the similarities of s(8,3) and s(8,1) in Figure 1, their in-neighbouring grids are shown in Figure 2. Note that $\left | {{I}_{3}} \right |=3$ and $\left | {{I}_{1}} \right |=2$, which implies that the similarity values of s(8,3) and s(8,1) should be different. However, $\left | {{M}_{8,3}} \right |=\left | {{M}_{8,1}} \right |=2$. Therefore, if we replace $\left | {{M}_{a,b}} \right |$ with $\left | {{I}_{a}} \right |+\left | {{I}_{b}} \right |-\left | {{M}_{a,b}} \right |$ in (1), the similarity values of s(8,3) and s(8,1) are considered as the same because

$$ \begin{array}{@{}rcl@{}} s(8,3) &=&\tfrac{\beta }{| {{M}_{8,3}} |}\big(s(13,9)+s(12,10) \big)+(1-\beta )=\tfrac{\beta }{2}(0.2+0.28 )+(1-\beta ) \\ s(8,1) &=&\tfrac{\beta }{| {{M}_{8,1}} |}\big(s(13,4)+s(12,5) \big)+(1-\beta )=\tfrac{\beta }{2}(0.2+0.28 )+(1-\beta ) \end{array} $$

Fig. 2

A demonstration on the affect of maximum matching denominator on similarity values

which is counter-intuitive to our common sense due to |I₁|≠|I₃|. However, if we use (2), then the similarity values of s(8,3) and s(8,1) become

$$ \begin{array}{@{}rcl@{}} s(8,3) &=&\tfrac{\beta }{| {{I}_{8}} |+| {{I}_{3}} |-| {{M}_{8,3}} |}\big(s(13,9)+s(12,10) \big)+(1-\beta )=\tfrac{\beta }{3}(0.2+0.28 )+(1-\beta ) \\ s(8,1) &=&\tfrac{\beta }{| {{I}_{8}} |+| {{I}_{1}} |-| {{M}_{8,1}} |}\big(s(13,9)+s(12,10) \big)+(1-\beta )=\tfrac{\beta }{2}(0.2+0.28 )+(1-\beta ) \end{array} $$

The larger the difference between $\left | {{I}_{3}} \right |$ and $\left | {{I}_{1}} \right |$, the more dissimilar the similarity scores of s(8,3) and s(8,1), which follows our intuition.

The relative weight of Part 1 and 2 is balanced by a user-controlled parameter λ ∈ [0,1]. β is a damping factor between 0 and 1, which is often set to 0.6 or 0.8, implying that similarity propagation made with distant in-neighbors is penalised by an attenuation factor β across edges. When I_a (or I_b) = ∅, which implies the maximum matching M_a,b = ∅, we define Part 1 and Part 2 to be 0 in order to avoid the denominators of the fraction in Part 1 and 2 being zeros.

Fixed-Point Iteration

To solve RoleSim* similarity s(a,b) in (1), we adopt the following fixed-point iterative scheme:

$$ \begin{array}{@{}rcl@{}} s_{0}(a,b) &=& 1 \qquad (\forall a, b) \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} s_{k+1}(a,b) &=& \beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{s}_{k} (x,y)} \\ &+& {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{s}_{k} (x,y)} \bigg)+(1-\beta ) \end{array} $$

(4)

where s_k(a,b) denotes the RoleSim* score between nodes a and b at iteration k. Based on (3) and (4), we can iteratively compute all pairs of similarity scores s_k+ 1(∗,∗) from those at the last iteration s_k(∗,∗).

3.2 Axiomatic properties for RoleSim*

Symmetry, Boundedness, & Monotonicity

Based on the definition of iterative similarity s_k(a,b) in (3) and (4), we next show three axiomatic properties of RoleSim*, i.e., symmetry, boundedness, and non-increasing monotonicity, based on the following theorem.

Theorem 1

The iterative RoleSim* {s_k(a,b)} in (3) and (4) have the following key properties: for any node-pair (a,b) and each iteration k = 0,1,⋯,

• 1. (Symmetry) s_k(a,b) = s_k(b,a)

• 2. (Boundedness) 1 − β ≤ s_k(a,b) ≤ 1

• 3. (Monotonicity) s_k+ 1(a,b) ≤ s_k(a,b)

Proof

• 1. (Symmetry) By virtue of (3) and (4), s_k(a,b) = s_k(b,a) follows immediately.

• 2. (Boundedness) We will prove this by induction on k. For k = 0, it is apparent that s₀(a,b) = 1 ∈ [1 − β,1]. For k > 0, we assume that s_k(x,y) ≤ 1 holds, and will prove that s_k+ 1(x,y) ≤ 1 holds as follows. Since

$$ \begin{array}{@{}rcl@{}} P_{1} & := &{\frac{1}{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}} \!\!\! \underbrace{{s}_{k} (x,y)}_{\le 1}} \le {\frac{|{M}_{a,b}|}{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}} \\ & =& \frac{\min\{|I_{a}|, |I_{b}|\}}{\max\{|I_{a}|, |I_{b}|\}} \le 1 \\ P_{2} & :=& \frac{1}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}\underbrace{{s}_{k} (x,y)}_{\le 1} \le \frac{\left| {{I}_{a}} \times {{I}_{b}} - {{M}_{a,b}} \right|}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}=1 \end{array} $$

Thus, (4) can be rewritten as

$$s_{k+1}(a,b) = \beta \times \big(\lambda \times \underbrace{P_{1}}_{\le 1} +(1-\lambda) \times \underbrace{P_{2}}_{\le 1} \big) + (1-\beta) \le 1 $$

On the other hand,

$$ s_{k+1}(a,b) = \underbrace{\beta \times \big(\lambda \times P_{1} +(1-\lambda) \times P_{2} \big)}_{\ge 0} + (1-\beta) \ge 1-\beta $$

• 3. (Monotonicity) We will prove by induction on k. For k = 0, s₀(a,b) = 1. According to (4), it follows that

$$ \begin{array}{@{}rcl@{}} {s}_{1}(a,b) & =&\beta \times \bigg(\lambda \times \underbrace{\frac{\min \{\left| {{I}_{a}} \right|,\left| {{I}_{b}} \right|\}}{\max \{\left| {{I}_{a}} \right|,\left| {{I}_{b}} \right|\}}}_{\le 1}+(1-\lambda )\times \underbrace{\frac{(\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|)-\left| M_{a,b} \right|}{(\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|)-\left| M_{a,b} \right|}}_{=1}\bigg)+(1-\beta ) \\ & \le& \beta (\lambda +(1-\lambda ))+(1-\beta )=1={{s}_{0}}(a,b) \end{array} $$

For k > 0, we assume that s_k+ 1(a,b) ≤ s_k(a,b) holds, and will prove that s_k+ 2(a,b) ≤ s_k+ 1(a,b) holds. According to (4), it follows that

$$ \begin{array}{@{}rcl@{}} s_{k+2}(a,b) &=& \beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}\overbrace{{s}_{k+1} (x,y)}^{{\qquad \textrm{\{using hypothesis\}} \ \le {s}_{k} (x,y)}}} \\ & \qquad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \underbrace{{{s}_{k+1} (x,y)}}_{\le {s}_{k} (x,y) } } \bigg)+(1-\beta ) \\ & \le& \beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{{s}_{k} (x,y)}} \\ & \qquad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} {{s}_{k} (x,y)} } \bigg)+(1-\beta ) \\ & =& s_{k+1}(a,b) \end{array} $$

□

Theorem 1 indicates that, for every iteration k = 0,1,2,⋯, {s_k(a,b)} is a bounded symmetric scoring function. Moreover, as $k \to \infty$, it can be readily verified that the exact solution s(a,b) also is a bounded symmetric measure, which is similar to SimRank and RoleSim measures. In contrast, other measures (e.g., Hitting Time and Random Walk with Restart) are asymmetric.

It is worth noticing that, unlike SimRank iterative similarity values {s_k(a,b)} that exhibit a non-decreasing trend (starting from 0 for any two distinct nodes a and b) w.r.t. the number of iterations k, RoleSim iterative similarity scores {s_k(a,b)} show a non-increasing tendency (starting from 1 for any two distinct nodes a and b) w.r.t.k. This subtle difference makes many existing optimization techniques on SimRank not directly applicable to RoleSim*.

Existence & Uniqueness

The bounded property and non-increasing property of RoleSim* iterative similarity values {s_k(a,b)} w.r.t.k guarantee the existence and uniqueness of the exact RoleSim* solution s(a,b) to (3) and (4), as indicated below:

Theorem 2 (Existence and Uniqueness)

There exists a unique solution s(a,b) (i.e., the exact RoleSim score) to (3) and (4) such that the iterative RoleSim similarity {s_k(a,b)} non-increasingly converges to it as the number of iterations k increases, i.e.,

$$ \lim_{k \to \infty} s_{k}(a,b) = s(a,b). $$

Proof

(Existence) For each pair of nodes (a,b), since the sequence {s_k(a,b)}_k is lower-bounded by (1 − β) (Property 2) and non-increasing (Property 3), by Monotone Convergence Theorem, {s_k(a,b)} will converge to its infimum, denoted as s(a,b), which is the exact RoleSim* solution, i.e., $\lim _{k \to \infty } s_{k}(a,b) = s(a,b)$.

(Uniqueness) For each pair of nodes (a,b), suppose there exist two solutions, s(a,b) and $\tilde {s}(a,b)$, that satisfy (4). We will prove that $s(a,b)=\tilde {s}(a,b)$. Let $\delta (a,b) := s(a,b)-\tilde {s}(a,b)$ and ${\varDelta } := \max \limits _{(a,b)} \{|\delta (a,b)|\}$. Then,

$$ \begin{array}{@{}rcl@{}} \delta(a,b) & = &s(a,b)-\tilde{s}(a,b) \\ &=& \beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}\overbrace{{s}(x,y)-\tilde{s}(x,y)}^{{= {\delta} (x,y)}}} \\ & \qquad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \underbrace{{s}(x,y)-\tilde{s}(x,y)}_{= {\delta} (x,y) } } \bigg) \end{array} $$

Therefore, taking the absolute value of both sides and applying triangle inequality |x + y|≤|x| + |y| produces

$$ \begin{array}{@{}rcl@{}} |\delta(a,b)| & \le &\beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|} \times \bigg| \sum\limits_{(x,y)\in {{M}_{a,b}}}{{\delta}(x,y)} \bigg| } \\ & \qquad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|} \times \bigg| \sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} {{\delta}(x,y)} \bigg| } \bigg) \\ & \le& \beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|} \times \sum\limits_{(x,y)\in {{M}_{a,b}}} \underbrace{\big| {{\delta}(x,y)} \big|}_{\le {\varDelta}} } \\ & \qquad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|} \times \sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \underbrace{\big| {{\delta}(x,y)} \big|}_{\le {\varDelta}} } \bigg) \\ & \le& \beta (\lambda \times {\varDelta} +(1-\lambda ) \times {\varDelta} ) =\beta \times {\varDelta} \qquad (\forall a, b) \end{array} $$

Thus, ${\varDelta }= \underset {(a,b) }{{\max \limits }} \{|\delta (a,b)|\} \le \beta \times {\varDelta }$, implying Δ = 0, i.e., $s(a,b)=\tilde {s}(a,b)$. □

3.3 Iterative RoleSim* algorithm with guaranteed accuracy

In this section, we provide an iterative algorithm for retrieving RoleSim* similarity values, and give a concise error bound for the difference between iterative similarity scores as provided by our algorithm and actual (exact) scores.

Iterative Algorithm

The fixed-point scheme in (3) and (4) implies an iterative algorithm for RoleSim* computation, as illustrated in Algorithm 1. It starts initialising all pairs of similarities to 1 (line 1), and carries out iterative computations of similarities for each pair of nodes (lines 3–15). If there are no in-neighbors for node a or b, s(a,b) is set to 1 − β (lines 4–6). Otherwise, it finds maximum weighed matching M_a,b in bipartite graph (I_a ∪ I_b,I_a × I_b) (line 8), and averages the (k − 1)-th iterative similarities over M_a,b (resp. (I_a × I_b) − M_a,b) to get w₁ (resp.w₂) (lines 9–14). Then, the weighted average of w₁ and w₂ is returned as score s_k(a,b) at k-th iteration. This process continues till all pairs of similarities are computed for each iteration.

Complexity The computational cost of Algorithm 1 is shown in Theorem 3.

Theorem 3

It requires O(K|E|²) time and O(|V |²) memory for Algorithm 1 to retrieve RoleSim* similarity scores for |V |² node-pairs on graph G = (V,E) with |V | nodes and |E| edges for K iterations.

Proof

For each iteration k and each pair of nodes (a,b), the computational time and memory required in each loop iteration of Algorithm 1 (lines 4–15) are described as follows:

Line	Time	Memory	Description
4	O(|Ia| + |Ib|)	O(|Ia| + |Ib|)	get in-neighborings for node a and b
6	O(1)	O(1)	initialise sk(a,b) if a and b have no in-neighbors
8	O(|Ia| + |Ib|)	O(|Ia|×|Ib|)	finding the maximum matching in a weighted bipartite graph using Jonker-Volgenant algorithm [2]
9	O(1)	O(1)	initialise t1 and t2
10–11	O(|Ma,b|)	O(1)	iteratively compute t1
12–13	O(|Ia|×|Ib|−|Ma,b|)	O(1)	iteratively compute t2
14–15	O(1)	O(1)	iteratively compute sk(a,b)

Thus, for K iterations and |V |² node-pairs, the total time of Algorithm 1 is bounded by

$$ \begin{array}{@{}rcl@{}} && \textstyle O \left( \sum\limits_{(a,b) \in V^{2}} \big(K (2(|I_{a}|+|I_{b}|) + (|I_{a}| \times |I_{b}|- |M_{a,b}|) +|M_{a,b}| \big) \right) \\ &= & \textstyle O \Big(K \sum\limits_{(a,b) \in V^{2}} \big(|I_{a}| \times |I_{b}| \big) \Big) = \textstyle O \left( K \underbrace{\textstyle \sum\limits_{a \in V} |I_{a}|}_{=|E|} \times \underbrace{\textstyle \sum\limits_{b \in V} |I_{b}|}_{=|E|} \right) = O(K{|E|}^{2}) \end{array} $$

Therefore, it entails O(K|E|²) time to retrieve |V |² pairs of RoleSim* scores.

Since |V |² pairs of similarities s_k− 1(∗,∗) at iteration (k − 1) need to be prepared for retrieving s_k(a,b) at next iteration k, the memory consumption of Algorithm 1 is bounded by O(|V |²). □

It is important to note that the O(|V |²) memory of Algorithm 1 hinders the scalability of RoleSim* computation on large graphs with millions of nodes. Therefore, in Section 5, on the top of Algorithm 1, we will propose a scalable algorithm for efficient RoleSim* similarity search on sizable graphs without loss of accuracy.

Error Bound

We are now ready to investigate the error bound of the difference between the k-th iterative similarity s_k(a,b) and exact one s(a,b).

By virtue of the non-increasing monotonicity of {s_k(a,b)}, one can readily show that the exact s(a,b) is the lower bound of all the iterative similarities {s_k(a,b)}, i.e.,s_k(a,b) ≥ s(a,b) (∀k). The following theorem further provides a concise upper bound to measure the closeness between s_k(a,b) and s(a,b).

Theorem 4 (Error Bound for Iterative RoleSim*)

For every iteration k = 0,1,2,⋯, the difference between s_k(a,b) and s(a,b) is bounded by

$$ s_{k}(a,b) - s(a,b) \le \beta^{k+1} \qquad (\forall a,b) $$

(5)

Proof

We prove this by induction on k. For k = 0, s₀(a,b) = 1. According to Property 2 of Theorem 1, 1 − β ≤ s_k(a,b) ≤ 1, implying that 1 − β ≤ s(a,b) ≤ 1. Thus, s₀(a,b) − s(a,b) ≤ β holds.

For k > 0, we assume that s_k(a,b) − s(a,b) ≤ β^k+ 1 holds, and will prove that s_k+ 1(a,b) − s(a,b) ≤ β^k+ 2 holds. Subtracting (4) from (1) produces

$$ \begin{array}{@{}rcl@{}} s_{k+1} (a,b)-s(a,b) &= &\beta \times \bigg({\frac{\lambda }{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}\overbrace{{s}_{k} (x,y)-{s}(x,y)}^{{\le \beta^{k+1}}}} \\ & \quad &+ {\frac{1-\lambda}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \underbrace{{s}_{k} (x,y)-{s}(x,y)}_{\le \beta^{k+1}} } \bigg) \\ & \le& \beta (\lambda \times \beta^{k+1} +(1-\lambda ) \times\beta^{k+1} ) = \beta^{k+2} \qquad (\forall a, b) \end{array} $$

□

Theorem 4 derives a concise exponential upper bound for the difference between the k-th iterative similarity s_k(a,b) and exact s(a,b). Combining this bound with the non-increasing monotonicity s_k(a,b) ≥ s(a,b), we can obtain that the k-th iterative error s_k(a,b) − s(a,b) is between 0 and β^k+ 1. Moreover, Theorem 4 also implies that, given desired accuracy 𝜖 > 0, the total number of iterations required for computing RoleSim* similarity is $k = \lceil \log _{\beta } \epsilon \rceil$.

It is worth noticing that the equality sign in our error estimation (5) is reachable, highlighting the tightness of the bound, as illustrated in Example 3.

Example 3

Consider the graph G in Figure 3. Given β = 0.8 and λ = 0.7, let us evaluate the RoleSim* similarity s(c,d) iteratively via (3) and (4). For iteration k = 0, it is apparent that s₀(∗,∗) = 1. When k = 1, it follows from |I_c| = |I_d| = |M_c,d| = 2 and (4) that

$$ s_{1}(c,d) = 0.8 \times \big(\tfrac{0.7}{2+2-2} \times (1+1) + \tfrac{1-0.7}{2 \times 2-2}\times (1+1) \big)+(1-0.8 ) = 1 $$

Since the exact solution is s(c,d) = 0.36, when k = 1, we have

$$ s_{1}(c,d) - s(c,d) = 1 - 0.36 = 0.64 = 0.8^{1+1} = \beta^{k+1} $$

Therefore, the equality in (5) is attainable on G when (k,β) = (1,0.8).

Fig. 3

The equality sign in our estimate bound (5) for iterative RoleSim* computation is attainable, e.g., it can be verified from graph G that there exist (k,β) = (1,0.8) such that s₁(c,d) − s(c,d) = 1 − 0.36 = 0.8^{1 + 1} = β^k+ 1 holds

4 Threshold-based RoleSim*

In this section, we propose our threshold-based RoleSim* model that substantially speeds up the computation of RoleSim* similarities with only a little sacrifice in accuracy. We will establish provable error bounds on our threshold-based RoleSim* model with respect to a user-specified threshold parameter δ, which is a speed-accuracy tradeoff.

Through the iterative computation of RoleSim* via (3) and (4), we notice that there are a significant number of node-pairs whose iterative similarity scores s_k(∗,∗) are very close to their convergent values s(∗,∗) and thus will not change much in subsequent iterations as k grows. To accelerate RoleSim* computation, we have the following two observations for eliminating such pairs from the unnecessary RoleSim* computations, with guaranteed accuracy.

Observation 1

If the RoleSim* similarity scores of two adjacent iterations, s_k− 1(∗,∗) and s_k(∗,∗), become quite close to each other after some iterations, then the RoleSim* iterative sequence {s_k(∗,∗)} from some iteration k₀ onwards are very close to the exact solution s(∗,∗) as well.

This observation is based on Cauchy Convergence Criterion to test whether a sequence has a limit. Precisely, for any small user-specified threshold δ > 0, this criterion implies that

$$ \lim_{k \to +\infty} s_{k}(*,*) = s(*,*) \ \Leftrightarrow \ \exists k_{0} \ \ \textit{s.t.~} \ \ |s_{k}(*,*)-s_{k+1}(*,*)|< \delta \quad (\forall k>k_{0}) $$

We apply this criterion to skip unnecessary iterative computations for node-pairs whose RoleSim* scores of two consecutive iterations are very small. More specifically, after some iterations, once the gap between s_k− 1(∗,∗) and s_k(∗,∗) is below the threshold δ, instead of employing (4) to iteratively compute s_k+ 1(∗,∗) from s_k(∗,∗), we simply supersede s_k+ 1(∗,∗) by the value of s_k(∗,∗). Therefore, we define the following threshold-based RoleSim* similarity ${\overline {s}}_{k}^{\delta }(*,*)$ based on Observation 1:

${\overline {s}}_{0}^{\delta }(a,b) = 1$

To quantify the difference between the threshold-based RoleSim* similarity ${\overline {s}}_{k}^{\delta }(*,*)$ in (6) and the conventional one s_k(∗,∗) in (4) at each iteration k, we show the following theorem.

Theorem 5

Given a threshold δ, for any number of iterations k = 0,1,2,⋯, there exists a positive integer k₀ such that for any k > k₀ and two nodes (a,b),

$$ {\overline{s}}_{k}^{\delta }(a,b) - {{s}_{k}}(a,b) \le \epsilon_{0} \ \ \text{ with } \ \ {{\epsilon }_{0}}=\tfrac{\beta (1-{{\beta }^{k-{{k}_{0}}}})}{1-\beta }\delta $$

(7)

where k₀ is the minimum integer that guarantees ${\overline {s}}_{{{k}_{0}}-1}^{\delta }(a,b)-{\overline {s}}_{{{k}_{0}}}^{\delta }(a,b)<\delta$.

Proof

When k = 0, it is apparent that ${{s}_{0}}(a,b)={\overline {s}}_{0}^{\delta }(a,b)=1$.

Let k₀ be the minimum integer that guarantees ${\overline {s}}_{{{k}_{0}}-1}^{\delta }(a,b)-{\overline {s}}_{{{k}_{0}}}^{\delta }(a,b)<\delta$ for any two nodes a and b. When 0 < k < k₀, in the case of ${\overline {s}}_{k-1}^{\delta }(a,b)-{\overline {s}}_{k}^{\delta }(a,b)\ge \delta$, ${\overline {s}}_{k}^{\delta }(a,b)$ is iteratively computed from (6a). Hence,

$${\overline{s}}_{k}^{\delta }(a,b)={{s}_{k}}(a,b)\quad (\forall k=0,1,{\cdots} ,{{k}_{0}}, \ \ \forall a, b).$$

When k ≥ k₀, in the case of ${\overline {s}}_{k-1}^{\delta }(a,b)-{\overline {s}}_{k}^{\delta }(a,b)<\delta$ for any nodes a and b, ${\overline {s}}_{k+1}^{\delta }(a,b)$ is directly obtained by (6b), thereby leading to its deviation from s_k+ 1(a,b) since the k₀-th iteration. In this case, to quantify the gap between ${\overline {s}}_{k+1}^{\delta }(a,b)$ and s_k+ 1(a,b), we notice that

$$ \begin{array}{@{}rcl@{}} && {{s}_{{{k}_{0}}}}(a,b)-{{s}_{{{k}_{0}}+1}}(a,b) \\ &= & \beta \times \bigg(\frac{\lambda }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{\underbrace{({{s}_{{{k}_{0}}-1}}(x,y)-{{s}_{{{k}_{0}}}}(x,y))}_{\le \delta }} \\ & &+\frac{1-\lambda }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{\underbrace{({{s}_{{{k}_{0}}-1}}(x,y)-{{s}_{{{k}_{0}}}}(x,y))}_{\le \delta }} \bigg) \\ &\le & \beta \times \bigg(\frac{\lambda \times \left( |{{M}_{a,b}}| \times \delta \right) }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}+\frac{(1-\lambda ) \times \left( |{{I}_{a}}| \times |{{I}_{b}}|-|{{M}_{a,b}}| \right) \times \delta }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}\bigg) \\ &\le & \beta \times (\lambda \times \delta +(1-\lambda ) \times \delta ) = \beta \times \delta \end{array} $$

Similarly,

$$ \begin{array}{@{}rcl@{}} & &{{s}_{{{k}_{0}}+1}}(a,b)-{{s}_{{{k}_{0}}+2}}(a,b) \\ &= & \beta \times \bigg(\frac{\lambda }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{\underbrace{({{s}_{{{k}_{0}}}}(x,y)-{{s}_{{{k}_{0}}+1}}(x,y))}_{\le \beta \times \delta }} \\ & &+\frac{1-\lambda }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{\underbrace{({{s}_{{{k}_{0}}}}(x,y)-{{s}_{{{k}_{0}}+1}}(x,y))}_{\le \beta \times \delta }} \bigg) \\ &\le & {{\beta }^{2}}\times \delta \end{array} $$

Iteratively, we can obtain that

$$ {{s}_{{{k}_{0}}+i-1}}(a,b)-{{s}_{{{k}_{0}}+i}}(a,b)\le {{\beta }^{i}}\times \delta \qquad (\forall i=0,1,2,{\cdots} ) $$

Since ${\overline {s}}_{k}^{\delta }(a,b)={\overline {s}}_{{{k}_{0}}}^{\delta }(a,b)={{s}_{{{k}_{0}}}}(a,b)\quad (\forall k\ge {{k}_{0}})$, it follows that

$$ \begin{array}{@{}rcl@{}} && {\overline{s}}_{k}^{\delta }(a,b)-{{s}_{k}}(a,b) = {{s}_{{{k}_{0}}}}(a,b)-{{s}_{k}}(a,b) \\ &= & \underbrace{\left( {{s}_{{{k}_{0}}}}(a,b)-{{s}_{{{k}_{0}}+1}}(a,b) \right)}_{\le \beta \times \delta }+\underbrace{\left( {{s}_{{{k}_{0}}+1}}(a,b)-{{s}_{{{k}_{0}}+2}}(a,b) \right)}_{\le {{\beta }^{2}}\times \delta }+{\cdots} +\underbrace{\left( {{s}_{k-1}}(a,b)-{{s}_{k}}(a,b) \right)}_{\le {{\beta }^{k-{{k}_{0}}}}\times \delta } \\ &\le & \delta \times {\sum}_{i=1}^{k-{{k}_{0}}}{{{\beta }^{i}}}=\delta \times \frac{\beta (1-{{\beta }^{k-{{k}_{0}}}})}{1-\beta } \quad (\forall k\ge {{k}_{0}}) \end{array} $$

□

Theorem 5 indicates that the threshold δ is a user-controlled parameter, which is a speed-accuracy trade-off. A small setting of δ ensures a high accuracy of ${\overline {s}}_{k}^{\delta }(*,*)$, but at the cost of more time for iterations, since only a small number of node-pairs can be pruned. In contrast, larger δ can discard more pairs of nodes from iterative computations, but would produce a larger error bound 𝜖₁ between ${\overline {s}}_{k}^{\delta }(*,*)$ and s_k(∗,∗).

Example 4

Consider the graph G in Figure 4a. Given threshold δ = 0.01, decay factor β = 0.6, and relative weight λ = 0.8, for pair (a,b) = (2,3), in Figure 4b, we see that

$$\bar{s}_{3}^{0.01}(2,3)-\bar{s}_{4}^{0.01}(2,3)=0.7139-0.7077=0.0062<\delta =0.01.$$

Thus, there exists an integer k₀ = 4, such that the error bound in (7) holds for all k > k₀, as depicted in Figure 4c. For example, when k = 10, we have

$$\bar{s}_{10}^{0.01}(2,3)-{{s}_{10}}(2,3)=0.7077-0.7=0.0077\le {{\epsilon }_{0}}$$

$$ \text{with } \ {{\epsilon }_{0}}=\tfrac{\beta (1-{{\beta }^{(k-{{k}_{0}})}})}{1-\beta }\delta =\tfrac{0.6\times (1-{{0.6}^{10-4}})}{1-0.6}\times 0.01=0.0143. $$

__

On the top of Observation 1, to enable a further speedup in the computation of RoleSim*, our second observation for discarding unnecessary RoleSim* iterations is the following:

Observation 2

For a given threshold δ, after some iterations, if the RoleSim* similarity score s_k(∗,∗) is within a small δ-neighbourhood of (1 − β), then the RoleSim* iterative sequence {s_k(∗,∗)} from some iteration k₁ onwards is also within the δ-neighbourhood of (1 − β).

Fig. 4

Error bound on the gap ${\overline {s}}_{k}^{\delta }(2,3)-{{s}}_{k}^{\delta }(2,3)$ based on Observation

This observation comes from the non-increasing property and lower bound of the RoleSim* iterative sequence $\{s_{k}(*,*)\}_{k=1}^{\infty }$ that we derived in Theorem 1. We notice that there are a number of pairs whose iterative RoleSim* similarity scores are very close to the lower bound (1 − β), but have not converged to the exact value of (1 − β) yet. Iteratively computing such pairs via (4) till convergence is cost-inhibitive. We observe that, when s_k(∗,∗) becomes close to (1 − β), the value of s_k+ 1(∗,∗) in the subsequent iteration is even closer to (1 − β) than s_k(∗,∗). As a result, there are opportunities to terminate earlier the iterative computations of s_k+i(∗,∗) by simply replacing the value of s_k+i(∗,∗) with (1 − β) for all i = 1,2,⋯, once s_k(∗,∗) falls into the δ-neighborhood of (1 − β), as illustrated below:

${\underline {s}}_{0}^{\delta }(a,b) = 1$

To distinguish ${\overline {s}}_{k}^{\delta }(*,*)$ in (6), we denote by ${\underline {s}}_{k}^{\delta }(*,*)$ in (8) the threshold-based RoleSim* similarity based on Observation 2. By definition, it is discerned that ${\underline {s}}_{k}^{\delta }(*,*) \le s_{k}(*,*) \le {\overline {s}}_{k}^{\delta }(*,*)$. The following theorem provides the bound for the difference between s_k(∗,∗) in (4) and ${\underline {s}}_{k}^{\delta }(*,*)$ in (8).

Theorem 6

Given a threshold δ, for any number of iterations k = 0,1,2,⋯, there exists a positive integer k₁ such that for any k ≥ k₁ and two nodes (a,b), it follows that

$$ \begin{array}{@{}rcl@{}} &&{{s}_{k}}(a,b)-{\underline{s}}_{k}^{\delta }(a,b) \le \epsilon_{1} \quad (\forall k\ge {{k}_{1}}) \\ &&\text{ with } \ \epsilon_{1} =\delta -\tfrac{{{\rho }^{{{k}_{1}}}}-{{\rho }^{k}}}{1-\rho }\times \xi, \quad \rho= \beta (1-\lambda), \quad \xi =1-\underset{(a,b)}{{\max }} \{{s_{1}(a,b)}\} \end{array} $$

(9)

where k₁ is the minimum integer that guarantees ${\underline {s}}_{{{k}_{1}}}^{\delta }(a,b) < 1-\beta + \delta$.

Proof

We first find the lower bound on the gap between s_k(a,b) and s_k+i(a,b). By definition of (4), when k = 0, it follows from s₀(∗,∗) = 1 that

$$ {{s}_{0}}(a,b)-{{s}_{1}}(a,b)=1-\beta \times \left( \frac{\lambda }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}\times |{{M}_{a,b}}|+(1-\lambda ) \right)-(1-\beta )$$

Plugging $|{{M}_{a,b}}|={\min \limits } (|{{I}_{a}}|,|{{I}_{b}}|)$ and $|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|={\max \limits } (|{{I}_{a}}|,|{{I}_{b}}|)$ to the above equation yields

$$ {{s}_{0}}(a,b)-{{s}_{1}}(a,b)={{\xi }_{a,b}} \ \text{ with } \ {{\xi }_{a,b}}=\lambda \beta \times \left( 1-\frac{\min (|{{I}_{a}}|,|{{I}_{b}}|)}{\max (|{{I}_{a}}|,|{{I}_{b}}|)} \right) $$

Let $\xi =\underset {a,b}{{{\min \limits } }} \{{{\xi }_{a,b}}\} =1-\underset {a,b}{{{\max \limits } }} \{{s_{1}(a,b)}\}$, we have

$${{s}_{0}}(a,b)-{{s}_{1}}(a,b)\ge \xi $$

When k = 1, it follows that

$$ \begin{array}{@{}rcl@{}} {{s}_{1}}(a,b)-{{s}_{2}}(a,b) & =&\beta \times \bigg(\frac{\lambda }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{\underbrace{\left( {{s}_{0}}(x,y)-{{s}_{1}}(x,y) \right)}_{\ge \xi }} \\ & \quad &+\frac{1-\lambda }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{\underbrace{\left( {{s}_{0}}(x,y)-{{s}_{1}}(x,y) \right)}_{\ge \xi }} \bigg) \\ & \ge& \beta \xi \times \bigg(\underbrace{\frac{\lambda |{{M}_{a,b}}|}{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}}_{\ge 0}+\underbrace{\frac{(1-\lambda) \times (|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}| ) }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}}_{=1-\lambda} \bigg) \\ & \ge& \rho \times \xi \quad \text{ with } \quad \rho = \beta (1-\lambda) \end{array} $$

Similarly, when k = 2, we have

$$ \begin{array}{@{}rcl@{}} {{s}_{2}}(a,b)-{{s}_{3}}(a,b) & =&\beta \times \bigg(\frac{\lambda }{|{{I}_{a}}|+|{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{\underbrace{\left( {{s}_{1}}(x,y)-{{s}_{2}}(x,y) \right)}_{\ge \rho \times \xi }} \\ & \quad &+\frac{1-\lambda }{|{{I}_{a}}|\times |{{I}_{b}}|-|{{M}_{a,b}}|}\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}}{\underbrace{\left( {{s}_{1}}(x,y)-{{s}_{2}}(x,y) \right)}_{\ge \rho \times \xi }} \bigg) \\ & \ge& \beta (1-\lambda) {{\rho } }\times \xi = {{\rho }^{2} }\times \xi \end{array} $$

Iteratively, we have

$${{s}_{k}}(a,b)-{{s}_{k+1}}(a,b)\ge {{\rho }^{k}} \times \xi \quad (\forall k=0,1,{\cdots} )$$

Therefore,

$$ \begin{array}{@{}rcl@{}} && {{s}_{k}}(a,b)-{{s}_{k+i}}(a,b) \\ &= & \underbrace{\left( {{s}_{k}}(a,b)-{{s}_{k+1}}(a,b) \right)}_{\ge {{\rho }^{k}} \times \xi } + \underbrace{\left( {{s}_{k+1}}(a,b)-{{s}_{k+2}}(a,b) \right)}_{\ge {{\rho }^{k+1}} \times \xi } + {\cdots} + \underbrace{\left( {{s}_{k+i-1}}(a,b)-{{s}_{k+i}}(a,b) \right)}_{\ge {{\rho }^{k+i-1}} \times \xi } \\ &\ge & {\sum}_{j=k}^{k+i-1} {{\rho }^{j}} \times \xi =\frac{{{\rho }^{k}}(1-{{\rho }^{i} })}{1- \rho }\times \xi \end{array} $$

(10)

Next, capitalising on the lower bound for s_k(a,b) − s_k+i(a,b), we are going to find the upper bound for ${{s}_{{{k}_{1}}+i}}(a,b)-{\underline {s}}_{{{k}_{1}}+i}^{\delta }(a,b)$. Let k₁ be the minimum integer that guarantees ${\underline {s}}_{{{k}_{1}}}^{\delta }(a,b)\le (1-\beta )+\delta$ for any two nodes a and b. Then, when k = k₁, we have

$${{s}_{{{k}_{1}}}}(a,b)={\underline{s}}_{{{k}_{1}}}^{\delta }(a,b)\le (1-\beta )+\delta \quad \Rightarrow \quad 1-\beta \ge {{s}_{{{k}_{1}}}}(a,b)-\delta $$

Iteratively, when k = k₁ + i (i ≥ 1), it follows from ${\underline {s}}_{{{k}_{1}}+i}^{\delta }(a,b)=1-\beta$ that

$$ \begin{array}{@{}rcl@{}} && {{s}_{{{k}_{1}}+i}}(a,b)-{\underline{s}}_{{{k}_{1}}+i}^{\delta }(a,b) \\ &= & {{s}_{{{k}_{1}}+i}}(a,b)-\underbrace{(1-\beta )}_{{\ge {{s}_{{{k}_{1}}}}(a,b)-\delta }}\le \delta -\underbrace{({{s}_{{{k}_{1}}}}(a,b)-{{s}_{{{k}_{1}}+i}}(a,b) )}_{\ge \frac{{{\rho }^{{{k}_{1}}}}(1-{{\rho }^{i}})}{1-\rho }\times \xi \text{ by (10)}}\le \delta -\tfrac{{{\rho }^{{{k}_{1}}}}(1-{{\rho }^{i}})}{1-\rho }\times \xi \end{array} $$

Thus,

$${{s}_{k}}(a,b)-{\underline{s}}_{k}^{\delta }(a,b)\le \epsilon_{1} \ \ \text{ with } \ \ \epsilon_{1} =\delta -\tfrac{{{\rho }^{{{k}_{1}}}}-{{\rho }^{k}}}{1-\rho }\times \xi \quad (\forall k\ge {{k}_{1}}) $$

□

Example 5

Consider the digraph G in Figure 5a. Given a threshold δ = 0.1, decay factor β = 0.2, and relative weight λ = 0.55, for node-pair (a,b) = (2,3), it is discerned that, when k grows to 3, the value of $\bar {s}_{k}^{\delta }(2,3)$ will fall into the δ-neighborhood of (1 − β), i.e.,$\bar {s}_{3}^{0.1}(2,3)=0.899<1-\beta +\delta =1-0.2+0.1=0.9$. Thus, there exists an integer k₁ = 3, such that the error bound in (9) holds for all k > k₁, as shown in Figure 5c. Then, e.g., when k = 4 (> k₁), we have

$$ \begin{array}{@{}rcl@{}} &&s_{4}(2,3)-\underline{s}_{4}^{\delta}(2,3)=0.89889-0.8000=0.09889 \leq \epsilon_{1} \\ &&\text{where } \rho= \beta (1-\lambda)=0.2 \times (1-0.55) = 0.09, \quad \xi =1-\underset{(a,b)}{{\max }} \{{s_{1}(a,b)}\} =0.09, \\ &&\text{and } {{\epsilon}_{1}}=\delta-\tfrac{\rho^{k_{1}}-\rho^{k}}{1-\rho} \xi =0.1-\tfrac{0.09^{3}-0.09^{4}}{1-0.09} \times 0.09 = 0.09993. \end{array} $$

Fig. 5

Error bound on the gap ${{s}}_{k}^{\delta }(2,3)-{\underline {s}}_{k}^{\delta }(2,3)$ based on Observation 2

Putting Them All Together

Combining Observations 1 and 2, we next propose the following complete scheme for threshold-based RoleSim* retrieval. To differentiate the notation from ${\overline {s}}_{k}^{\delta }(*,*)$ in (6) and ${\underline {s}}_{k}^{\delta }(*,*)$ in (8), we denote by ${{s}}_{k}^{\delta }(*,*)$ the threshold-based RoleSim* similarity for our complete scheme combining both Observations 1 and 2, which is defined as follows:

$s_{0}^{\delta }(a,b) = 1$

By virtue of Theorems 5 and 6, the following upper bound on the difference between $s_{k}^{\delta }(*,*)$ and s_k(∗,∗) is immediate.

Corollary 1 (Error Bound for Threshold-Based RoleSim* Iteration)

Given a threshold δ, for any number of iterations k = 0,1,2,⋯, there exist two positive integers k₀ and k₁ such that for any two nodes (a,b),

$$ |{{s}_{k}}(a,b)-s_{k}^{\delta }(a,b)|\le \epsilon \ \text{ with } \ \epsilon = \left\{ \begin{array}{*{35}{l}} \min \left\{ {{\epsilon}_{0}},{{\epsilon}_{1}} \right\} & \text{if}\ k\ge \max\left\{ {{k}_{0}},{{k}_{1}} \right\} \\ {{\epsilon}_{0}} & \text{if}\ {{k}_{0}}\le k\le {{k}_{1}} \\ {{\epsilon}_{1}} & \text{if}\ {{k}_{1}}\le k\le {{k}_{0}}\ \\ 0 & \text{if}\ 0\le k\le \min \left\{ {{k}_{0}},{{k}_{1}} \right\} \end{array} \right. $$

where ${{\epsilon }_{0}}=\tfrac {\beta (1-{{\beta }^{k-{{k}_{0}}}})}{1-\beta }\delta$, and ${{\epsilon }_{1}}= \delta -\frac {{{\rho }^{{{k}_{1}}}}-{{\rho }^{k}}}{1-\rho } \xi$ with ρ = β(1 − λ) and $\xi =1-\underset {a,b}{{{\max \limits } }} \{{s_{1}(a,b)}\}$; k₀ (resp.k₁) is the minimum positive integer that ensures $s_{{{k}_{0}}-1}^{\delta }(a,b)-s_{{{k}_{0}}}^{\delta }(a,b)<\delta$ (resp. $s_{{{k}_{1}}}^{\delta }(a,b) < 1-\beta + \delta$) holds.

5 Scaling RoleSim* search on large graphs

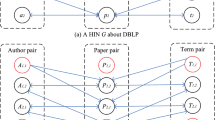
In this section, we propose efficient techniques that enable RoleSim* similarity search to scale well on sizable graphs with billions of edges. It is noticed that our iterative method for RoleSim* search by Algorithm 1 needs to memoise all |V |² pairs of similarities {s_k(∗,∗)} at iteration k for computing any similarity at iteration (k + 1). On small graphs, this algorithm runs very fast for all-pairs search. However, real graphs are often large with millions of nodes. The O(|V |²) memory required by Algorithm 1 would jeopardise its scalability over massive graphs. Moreover, in many real-world applications, users are often interested in partial-pairs similarity search. For instance, in a DBLP collaboration network, one would like to find who are Prof. Jennifer Widom’s close collaborators. In a social graph, one wants to know who are Thomas’s close friends on Instagram. In a web graph, one wishes to identify which web pages are relevant to a given query page. These applications call for a need to devise a scalable method that retrieves partial-pairs RoleSim* similarities within a small amount of memory. Formally, we are ready to solve the following RoleSim* search problem:

Problem (Single-source RoleSim* Similarity Search). Given: a graph G = (V,E), a query node q ∈ V, and a desired depth K¹

Retrieve: |V | pairs of RoleSim* similarities {s_K(∗,q)} between all nodes in G and query q in a scalable manner.

To avoid using O(|V |²) memory, the central idea underpinning our method is judiciously implementing caching techniques on only a small portion of node-pairs that involve heavily repetitive similarity computations. More specifically, to evaluate each pair (u,q)’s similarity for single-source {s(∗,q)} retrieval, we start at each root pair (u,q), and employ a depth-first search (DFS) to traverse all the in-neighboring pairs within k hops from the root (u,q), recursively, against the in-coming edges of the graph in a depthward movement before backtracking when a desired depth k is reached or a “dead end” (i.e., a pair (x,y) with either node x or y having no in-neighbours) occurs in any iteration. The iterative recurrence for retrieving each root pair (u,q) can be diagrammed by a recursion tree. For example, given graph G in Figure 6a with query node q = 7 and desired depth K = 4, the recursion tree for the recurrence to retrieve each s(x,7) (∀x ∈ V ) through DFS is depicted in Figure 6c, respectively. We have the following two observations:

• (1) There are a number of repeated computations among these recursion trees. For instance, s(4,7) is repetitively evaluated three times (circled in red). If the result of s(4,7) is cached and reused in subsequent recurrence, a number of unnecessary RoleSim* computations can be avoided.

• (2) When breaking down the traversal of s(3,7) and s(4,7), we notice that their unfolded recurrence structures (circled in blue) are exactly the same, which is due to the same in-neighboring structures of nodes 3 and 4, i.e.,I(3) = I(4). If the previously cached results of s(4,7) can be used again for evaluating any other {s(x,7)} (for all x ∈ V −{4} with the same in-neighboring structure of node 7), many duplicate computations can be skipped further.

It is worth mentioning that the parameter K here is the desired depth of search to control the height of the traversed recursion tree, which provides a user-controlled effect of the speed and accuracy for computing RoleSim* similarity. For example, when K is small, the computation of s_K(v,q) is fast, but this would increase the error between s_K(v,q) and the exact solution s(v,q). When K is large, s_K(v,q) approaches s(v,q), which achieves high accuracy, but will take more time, as it requires more steps to traverse the recursion tree. Moreover, the user-specified K also effectively avoid ending up an infinite loop of a circle while traversing the graph for RoleSim* retrieval.

Fig. 6

Single-source RoleSim* method that caches the similarities of important pairs eliminates many unnecessary recomputations in DFS backtracking

Based on these observations, we devise a caching approach in backtracking of DFS to minimise duplicate RoleSim* similarity computations. Different from Algorithm 1 that requires O(|V |²) memory space to cache all-pairs similarities, we select only the “important” pairs for memoization. We first define the “importance” of a node-pair as follows.

Definition 1

Let (x,y) be a pair of nodes, and |O_x| be the out-degree of node x, then the importance of the pair (x,y), denoted as ρ(x,y), is defined as

$$ \rho(x,y) := |O_{x}| \times |O_{y}| $$

Intuitively, Definition 1 uses degree centrality to evaluate the “importance” of a pair since a pair (x,y) is likely to be “important” if nodes x and y are linked to a large number of nodes.

According to Definition 1, during DFS backtracking, when each pair (x,y) is visited, we first check if ρ(x,y) ≥ 𝜃 to determine whether this pair is worthy of being cached, where 𝜃 is user-specified threshold between 0 and $d_{\max \limits }^{2}$², which is a space-speed tradeoff. When 𝜃 is set to 0, all pairs in the recursion tree are memoised, which in the worst case will reduce to the case of Algorithm 1. When $\theta > d_{\max \limits }^{2}$, no caching techniques apply, which degrades to the naive recursive retrieval of RoleSim* similarities, being rather cost-inhibitive. In other words, the selection of 𝜃 value is a trade-off problem between memory and execution time, the smaller the 𝜃, the larger the number of memoised pairs in memory and consequently the lower the execution time. Therefore, an appropriate selection of 𝜃 plays an important role in providing a good balance between the computational time and memory space (i.e., the number of memoised pairs to be retrieved).

To avoid caching insignificant pairs, we often set 𝜃 to the first quartile of the pairwise out-degree set $\{\rho (x,y)\}_{(x,y) \in V^{2}}$ of the graph, which guarantees more than slightly important pairs to be cached using a moderate amount of memory. This is because there are close relationships between 𝜃 and the number of retrieved pairs N. As demonstrated by our extensive experiments in Figure 7, when 𝜃 is less than the first quartile of the pairwise out-degree set $\{\rho (x,y)\}_{(x,y) \in V^{2}}$ on each dataset³ (e.g.,DBLP, Bitcoin-α and P2P), there are a large number of memoised pairs with huge space requirement, but the computation is very fast. When 𝜃 is larger than the first quartile of $\{\rho (x,y)\}_{(x,y) \in V^{2}}$, the execution time increases significantly whereas the number of retrieved pairs decreases sharply. Only when 𝜃 is around the first quartile of $\{\rho (x,y)\}_{(x,y) \in V^{2}}$ (e.g.,𝜃 ≈ 10 on DBLP, 5 on Bitcoin-α, 60 on P2P), there is a good balance between the computational time and memory space (with the balancing point circled in red). Thus, we empirically set 𝜃 to the first quartile of the pairwise out-degree set $\{\rho (x,y)\}_{(x,y) \in V^{2}}$ of a graph.

Fig. 7

An appropriate choice of 𝜃 provides a good balance between computational time and memory space (i.e., # of memorised pairs)

Once we decide that a visited pair (x,y) deserves to be cached, we next employ an unordered hash table ${\mathcal T}$ for memoising. Precisely, we first check whether the key (i.e., node-pair (x,y)) exists in the hash table. If not, we compute the RoleSim* similarity s(x,y) once, and add < key,value >:=< (x,y),s(x,y) > to the hash table. Otherwise, we just retrieve the cached similarity value s(x,y) corresponding to the key (x,y) from the hash table instead of computing the similarity s(x,y) again, thus significantly boosting the performance for single-source RoleSim* search. Note that, due to the symmetry of RoleSim* similarity s(x,y) = s(y,x), when hashing the pair (x,y), we will swap x and y beforehand if x > y, to avoid both (x,y) and (y,x) being hashed.

Single-Source Algorithm

The single-source RoleSim* algorithm, referred to as SSRS*, is shown in Algorithm 2. It works as follows. First, it starts by building a hash table ${\mathcal T}$ (line 1). Next, it invokes a Single-Pair function to evaluate the RoleSim* similarity between each node u ∈ G and query q according to whether the similarity value of pair (u,q) is memoised in hash table ${\mathcal T}$ (lines 2-6). If pair (u,q) is at the last level or has no in-neighbours, the similarity is set to (1 − β) (line 8). Otherwise, it enumerates all the in-neighboring pairs (a,b) in I_u × I_q (line 11). If (a,b) exists in hash table ${\mathcal T}$, it retrieves the similarity of (a,b) from ${\mathcal T}$ directly with no need for recomputation (line 13); otherwise, it recursively computes the similarity of (a,b) (line 15). Using all the similarities of the in-neighboring pairs of (u,q), it then computes similarity s(u,q) according to (4) (line 16-18), and memoises the resulting score if (u,q) is an important pair (line 19). Finally, it returns s(u,q) to the main function (line 20).

Computational Complexity

Analysing the computational time for retrieving single-source RoleSim* query, we show the following theorem:

Theorem 7

Let N be the number of pairs whose RoleSim* similarity scores are retrieved from the hash table in the traversal of the recursion tree with K levels. Assume that the network G is scale-free and follows power-law degree distribution. We denote by p_in(d) and p_out(d) the fraction of nodes in G having in-degree and out-degree d, respectively, which satisfy ${{p}_{\text {in}}}(d)\propto {{d}^{-{{\gamma }_{\text {in}}}}}$ and ${{p}_{\text {out}}}(d)\propto {{d}^{-{{\gamma }_{\text {out}}}}}$, where γ_in and γ_out are the power-law exponents whose values are typically $2\sim 3$. Let d_in and d_out be the maximum in-degree and out-degree of G, respectively. Then, the average computational time for retrieving RoleSim* similarities between all nodes and a query for K levels is bounded by $O\big ({{\rho }_{\text {out}}^{2(K-1)}} \left (|V|{{\rho }_{\text {out}}^{2}}-\frac {N}{K} \right ) \big )$ with ${{\rho }_{\text {out}}}:=O\left (\frac {{{({{d}_{\text {out}}})}^{2-{{\gamma }_{\text {out}}}}}-1}{2-{{\gamma }_{\text {out}}}} \right )$.

Proof

We first analyse the computational cost for a single-pair RoleSim* query without using any memoisation optimisation. Since the graph G follows power-law degree distribution, the expected value of the number of in-neighbours of each node is bounded by

$$ \begin{array}{@{}rcl@{}} & &\sum\limits_{d=1}^{{{d}_{\text{in}}}}{d\cdot {{p}_{\text{in}}}(d)} =\sum\limits_{d=1}^{{{d}_{\text{in}}}}{d\cdot {{C}_{\text{in}}}\cdot {{d}^{-{{\gamma }_{\text{in}}}}}}={{C}_{\text{in}}}\cdot \sum\limits_{d=1}^{{{d}_{\text{in}}}}{{{d}^{1-{{\gamma }_{\text{in}}}}}} \le {{C}_{\text{in}}}{\int}_{1}^{{{d}_{\text{in}}}}{{{x}^{1-{{\gamma }_{\text{in}}}}}dx} \\ &= & \textstyle \tfrac{{{C}_{\text{in}}}}{2-{{\gamma }_{\text{in}}}}\cdot {{x}^{2-{{\gamma }_{\text{in}}}}}\big|_{1}^{{{d}_{\text{in}}}} \big.={{\rho }_{\text{in}}} \quad \text{ with}\quad {{\rho }_{\text{in}}}:=\tfrac{{{C}_{\text{in}}}}{2-{{\gamma }_{\text{in}}}}\big({{d}_{\text{in}}^{2-{{\gamma }_{\text{in}}}}}-1 \big) \end{array} $$

where C_in is a constant. Similarly, the expected value of the number of out-neighbouring pairs of any pair is bounded by ${{\rho }_{\text {out}}}:=\tfrac {{{C}_{\text {out}}}}{2-{{\gamma }_{\text {out}}}}\big ({{({{d}_{\text {out}}})}^{2-{{\gamma }_{\text {out}}}}}-1 \big )$, where C_out is a constant. We notice that, to compute each pair of similarity at any level i, the expected value of the number of in-neighbouring pairs that we need to retrieve at level (i − 1) is $O({{\rho }_{\text {in}}}^{2})$. Since the expected value of the number of node-pairs at level i is bounded by $O({{\rho }_{\text {out}}}^{2(i-1)} )$ in the average case, the total computational time for evaluating any single-pair similarity at the top level in the average case is bounded by

$$ \textstyle O\left( \sum\limits_{i=1}^{K}{{{\rho }_{\text{out}}}^{2(i-1)}\cdot {{\rho }_{\text{in}}}^{2}} \right)=O\left( \frac{{{\rho }_{\text{in}}}^{2}}{{{\rho }_{\text{out}}}^{2}-1}\cdot \left( {{\rho }_{\text{out}}}^{2K}-1 \right) \right)=O\left( {{\rho }_{\text{out}}}^{2K} \right) $$

which implies that $O(|V|{{\rho }_{\text {out}}}^{2K})$ time is required for single-source retrieval of |V | nodes w.r.t. a query.

However, after using memoisation, this computational cost is significantly reduced. Generally, the amount of computational cost reduction depends on the number of memoised pairs and the position at which the memoised pairs appear. For ease of our analysis, we denote by C(i) the computational cost that can be saved by a pair at level i whose similarity value is obtainable directly from the hash table. Since the expected value of the number of out-neighboring pairs of similarities that need to be retrieved at level (i + 1) is bounded by $O({{\rho }_{\text {out}}}^{2})$ recursively till level K, the total computational cost of C(i) in the worst case is:

$$ \textstyle C(i)=1+{{{\rho }_{\text{out}}}^{2}}+{{{\rho }_{\text{out}}}^{4}}+{\cdots} +{{{\rho }_{\text{out}}}^{2(K-i)}}=\frac{{{{\rho }_{\text{out}}}^{2(K-i+1)}}-1}{{{{\rho }_{\text{out}}}^{2}}-1}$$

Then, the average computational cost, denoted as $\bar {C}$, which can be saved by a pair through retrieving its similarity score from the hash table, is as follows:

$$ \begin{array}{@{}rcl@{}} \bar{C} & = &\frac{1}{K}\sum\limits_{i=1}^{K}{i\times C(i)} = \frac{1}{K}\left( \sum\limits_{i=1}^{K}{i\times \left( \frac{{{{\rho }_{\text{out}}}^{2(K-i+1)}}-1}{{{{\rho }_{\text{out}}}^{2}}-1} \right)} \right) \\ & = &\frac{1}{K}\left( \frac{1}{{{{\rho }_{\text{out}}}^{2}}-1}\left( \sum\limits_{i=1}^{K}{i\times {{({{{\rho }_{\text{out}}}^{2}})}^{(K-i+1)}}}-\sum\limits_{i=1}^{K}{i} \right) \right) \\ & = &\frac{1}{K}\left( \frac{1}{{{{\rho}_{\text{out}}}^{2}}-1}\left( \frac{{{{\rho }_{\text{out}}}^{4}}({{{\rho }_{\text{out}}}^{2K}}-1)}{{{({{{\rho}_{\text{out}}}^{2}}-1)}^{2}}} - \frac{K{{\rho}_{\text{out}}}^{2}}{({{{\rho }_{\text{out}}}^{2}} - 1)} - \frac{(1 + K)K}{2} \right) \right) = O\left( \frac{{{{\rho }_{\text{out}}}^{2(K-1)}}}{K} \right). \end{array} $$

It follows that the average computational cost for a single-source query is

$$ \begin{array}{@{}rcl@{}} && O\left( |V|{{{\rho }_{\text{out}}}^{2K}} \right)-N\times \bar{C} =O\big(|V|{{\rho }_{\text{out}}^{2K}}-N \times \frac{{{\rho }_{\text{out}}^{2(K-1)}}}{K} \big) \\ &= & O\big({{\rho }_{\text{out}}^{2(K-1)}} \left( |V|{{\rho }_{\text{out}}^{2}}-\frac{N}{K} \right) \big) \quad \text{ with } \quad {{\rho }_{\text{out}}}:=O\left( \frac{{{({{d}_{\text{out}}})}^{2-{{\gamma }_{\text{out}}}}}-1}{2-{{\gamma }_{\text{out}}}} \right) \end{array} $$

□

6 “Sum-transitivity” of RoleSim* similarity

In this section, we investigate the transitive property of the proposed RoleSim* similarity measure. Intuitively, when a similarity measure s(∗,∗) fulfils the transitive property, it means that, for any three nodes a,b,c in the graph, if a is similar to b and b is similar to c, it implies that a is likely to be similar to c. The transitivity feature is useful in many real applications, e.g., for predicting and recommending links in a graph.

Before showing the transitive property of RoleSim*, let us induce a distance d(a,b) := 1 − s(a,b) from the RoleSim* measure. Due to s(∗,∗) ∈ [1 − β,1], the distance d(∗,∗) is between 0 and β. In what follows, we will show that d(∗,∗) satisfies the triangular inequality, which is an indication of s(∗,∗) transitivity.

We first provide the following two lemmas, which will lay the foundation for our proof of the RoleSim* triangular inequality.

Lemma 1

Let s_k(∗,∗) be the k-th iterative RoleSim* similarity via (3) and (4). For any 3 nodes (a,b,c) in a graph, if s_k(a,b) + s_k(b,c) − s_k(a,c) ≤ 1 holds at iteration k, the following inequality holds:

$$ \frac{\sum\limits_{(x,y)\in {{M}_{a,b}}}{{{s}_{k}}}(x,y)}{\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}+\frac{\sum\limits_{(y,z)\in {{M}_{b,c}}}{{{s}_{k}}}(y,z)}{\left| {{I}_{b}} \right|+\left| {{I}_{c}} \right|-\left| {{M}_{b,c}} \right|}-\frac{\sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}}(x,z)}{\left| {{I}_{a}} \right|+\left| {{I}_{c}} \right|-\left| {{M}_{a,c}} \right|} \le 1 $$

(12)

Proof

Without loss of generality, we only consider the case of $\left | {{I}_{a}} \right |\le \left | {{I}_{b}} \right |\le \left | {{I}_{c}} \right |$. The proofs for other cases are similar, and omitted here due to space limitation. In this case, we have

$$\left| {{I}_{a}} \right|+\left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|=\max \{\left| {{I}_{a}} \right|,\left| {{I}_{b}} \right|\}=\left| {{I}_{b}} \right|.$$

Hence, the left-hand side (LHS) of (12) can be rewritten as

$$ \begin{array}{@{}rcl@{}} && \text{LHS of (12)} \\ &= & \frac{1}{\left| {{I}_{b}} \right|}\sum\limits_{(x,y)\in {{M}_{a,b}}}{{{s}_{k}}}(x,y)+\frac{1}{\left| {{I}_{c}} \right|}\sum\limits_{(y,z)\in {{M}_{b,c}}}{{{s}_{k}}}(y,z)-\frac{1}{\left| {{I}_{c}} \right|}\sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}}(x,z) \\ &= & \overbrace{\left( \frac{1}{\left| {{I}_{b}} \right|}-\frac{1}{\left| {{I}_{c}} \right|} \right)\sum\limits_{(x,y)\in {{M}_{a,b}}}{{{s}_{k}}(x,y)}}^{\textrm{Part 1}} \\ & \quad &+ \frac{1}{\left| {{I}_{c}} \right|} \bigg(\underbrace{\sum\limits_{(x,y)\in {{M}_{a,b}}} \!\!\!\!\!\!\!\! {{{s}_{k}}(x,y)}+\sum\limits_{(y,z)\in {{M}_{b,c}}}\!\!\!\!\!\!\!\! {{{s}_{k}}(y,z)}-\sum\limits_{(x,z)\in {{M}_{a,c}}}\!\!\!\!\!\!\!\! {{{s}_{k}}(x,z)}}_{\textrm{Part 2}} \bigg) \end{array} $$

(13)

We first find an upper bound on Part 1. Since $\sum \limits _{(x,y)\in {{M}_{a,b}}}\!\!\!\!\!\!\! {{{s}_{k}}(x,y)} \le \!\!\!\!\!\!\!\!\! \sum \limits _{(x,y)\in {{M}_{a,b}}} \!\!\!\!\!{1} =|{{M}_{a,b}}|$, it follows that

$$ \textrm{Part 1} \le \left( \frac{1}{\left| {{I}_{b}} \right|}-\frac{1}{\left| {{I}_{c}} \right|} \right) \times \left| {{M}_{a,b}} \right|=\left( \frac{1}{\left| {{I}_{b}} \right|}-\frac{1}{\left| {{I}_{c}} \right|} \right) \times \left| {{I}_{a}} \right| $$

(14)

To get an upper bound for Part 2, let

$$ \begin{array}{@{}rcl@{}} {{{\tilde{I}}}_{b}} & =&\{y \ | \ \forall x\in {{I}_{a}},\quad \exists y\in {{I}_{b}},\quad s.t.\ (x,y)\in {{M}_{a,b}}\} \\ {{{\tilde{M}}}_{a,c}} & =&\{(x,z) \ | \ \exists y\in {{I}_{b}},\quad s.t.\ (x,y)\in {{M}_{a,b}}\ \wedge \ (y,z)\in {{M}_{b,c}}\} \end{array} $$

Then, M_b,c can be partitioned into two parts: ${{M}_{b,c}}=M_{b,c}^{(1)}\cup M_{b,c}^{(2)}$ where

$$ \begin{array}{@{}rcl@{}} M_{b,c}^{(1)} &=&\{(y,z)\in {{M}_{b,c}}\ |\ y\in {{{\tilde{I}}}_{b}}, \quad z\in {{I}_{c}}\} \\ M_{b,c}^{(2)} &=&\{(y,z)\in {{M}_{b,c}}\ |\ y\in {{I}_{b}}-{{{\tilde{I}}}_{b}}, \quad z\in {{I}_{c}}\} \end{array} $$

Therefore,

$$ \begin{array}{@{}rcl@{}} && \textrm{Part 2}=\sum\limits_{(x,y)\in {{M}_{a,b}}}{{{s}_{k}}(x,y)}+\sum\limits_{(y,z)\in {{M}_{b,c}}}{{{s}_{k}}(y,z)}-\sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}(x,z)} \\ & =&\bigg(\sum\limits_{(x,y)\in {{M}_{a,b}}}{{{s}_{k}}(x,y)}+\sum\limits_{(y,z)\in M_{b,c}^{(1)}}{{{s}_{k}}(y,z)} \bigg)+ \!\!\!\!\!\!\sum\limits_{(y,z)\in M_{b,c}^{(2)}}{\underbrace{{{s}_{k}}(y,z)}_{\le 1}} -\sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}(x,z)} \\ & \le& \bigg(\underbrace{\sum\limits_{(x,z)\in {{{\tilde{M}}}_{a,c}}}{{{s}_{k}}(x,z)}}_{\le \sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}(x,z)}}+\left| {{I}_{a}} \right| \bigg)+\Big(\underbrace{|{{M}_{b,c}}|}_{=\left| {{I}_{b}} \right|}-\underbrace{|{{{\tilde{I}}}_{b}}|}_{=\left| {{I}_{a}} \right|}\Big)- \!\!\!\!\!\!\sum\limits_{(x,z)\in {{M}_{a,c}}}{{{s}_{k}}(x,z)} \le \left| {{I}_{b}} \right| \end{array} $$

(15)

Substituting (14) and (15) into (13) produces

$$ \text{LHS of (12)} \le \left( \frac{1}{\left| {{I}_{b}} \right|}-\frac{1}{\left| {{I}_{c}} \right|} \right)\left| {{I}_{a}} \right|+\frac{\left| {{I}_{b}} \right|}{\left| {{I}_{c}} \right|}=\frac{\left| {{I}_{a}} \right|}{\left| {{I}_{b}} \right|}+\frac{\left| {{I}_{b}} \right|-\left| {{I}_{a}} \right|}{\left| {{I}_{c}} \right|} \le 1 $$

□

Lemma 2

For any 3 nodes (a,b,c) in a graph, if s_k(a,b) + s_k(b,c) − s_k(a,c) ≤ 1 holds at iteration k, then it follows that

$$ \frac{\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{{s}_{k}}(x,y)}}{\left| {{I}_{a}} \right|\times \left| {{I}_{b}} \right|-\left| {{M}_{a,b}} \right|}+\frac{\sum\limits_{(y,z)\in ({{I}_{b}}\times {{I}_{c}})-{{M}_{b,c}}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{{s}_{k}}(y,z)}}{\left| {{I}_{b}} \right|\times \left| {{I}_{c}} \right|-\left| {{M}_{b,c}} \right|}-\frac{\sum\limits_{(x,z)\in ({{I}_{a}}\times {{I}_{c}})-{{M}_{a,c}}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{{s}_{k}}(x,z)}}{\left| {{I}_{a}} \right|\times \left| {{I}_{c}} \right|-\left| {{M}_{a,c}} \right|} \le 1 $$

(16)

Proof

For each x ∈ I_a, there exist y_x ∈ I_b and z_x ∈ I_c such that (x,y_x) ∈ M_a,b and (x,z_x) ∈ M_a,c. Then, for each z ∈ I_c −{z_x}, there exists y ∈ I_b such that

$${{s}_{k}}(x,y)+{{s}_{k}}(y,z)-{{s}_{k}}(x,z)\le 1$$

Summing both sides of the inequality over all z ∈ I_c −{z_x} and all y ∈ I_b yields

$$ \underbrace{\sum\limits_{y\in {{I}_{b}}}^{\sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}} \!\!\!\!\!\!{{{s}_{k}}(x,y)}}}_{\textrm{Part 1}}+\underbrace{\sum\limits_{y\in {{I}_{b}}}{\sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}} \!\!\!\!\!\!{{{s}_{k}}(y,z)}}}_{\textrm{Part 2}}-\underbrace{\sum\limits_{y\in {{I}_{b}}}{\sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}} \!\!\!\!\!\!{{{s}_{k}}(x,z)}}}_{=|{{I}_{b}}|\times \sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}}{{{s}_{k}}(x,z)}}\le \left( |{{I}_{c}}|-1 \right)\times |{{I}_{b}}| $$

where

$$ \begin{array}{@{}rcl@{}} \textrm{Part 1} &=&(|{{I}_{c}}|-1)\times \sum\limits_{y\in {{I}_{b}}}^{{{s}_{k}}(x,y)}\ge (|{{I}_{c}}|-1)\times \sum\limits_{y\in {{I}_{b}}-\{{{y}_{x}}\}}^{{{s}_{k}}(x,y)} \\ \textrm{Part 2} &=&\sum\limits_{(y,z)\in ({{I}_{b}}\times {{I}_{c}})}{{{s}_{k}}(y,z)}-\underbrace{\sum\limits_{y\in {{I}_{b}}}{{{s}_{k}}(y,{{z}_{x}})}}_{\le \sum\limits_{(y,z)\in {{M}_{b,c}} }{{{s}_{k}}(y,{{z}})}} \ge \sum\limits_{(y,z)\in ({{I}_{b}}\times {{I}_{c}})-{{M}_{b,c}}}{{{s}_{k}}(y,z)} \end{array} $$

Therefore, it follows that

$$(|{{I}_{c}}|-1)\times \!\!\!\!\!\! \sum\limits_{y\in {{I}_{b}}-\{{{y}_{x}}\}} \!\!\!\!\!\!{{{s}_{k}}(x,y)}+ \!\!\!\!\!\! \sum\limits_{(y,z)\in ({{I}_{b}}\times {{I}_{c}})-{{M}_{b,c}}}\!\!\!\!\!\!{{{s}_{k}}(y,z)}-|{{I}_{b}}|\times \!\!\!\!\!\! \sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}} \!\!\!\!\!\!{{{s}_{k}}(x,z)}\le \left( |{{I}_{c}}|-1 \right)\times |{{I}_{b}}| $$

Summing both sides of the inequality over all x ∈ I_a produces

$$ \begin{array}{@{}rcl@{}} (|{{I}_{c}}|-1)\times & &\overbrace{ \sum\limits_{x\in {{I}_{a}}} {\sum\limits_{y\in {{I}_{b}}-\{{{y}_{x}}\}} \!\!\!\!\!\! {{{s}_{k}}(x,y)}}}^{=\sum\limits_{(x,y)\in ({{I}_{a}}\times {{I}_{b}})-{{M}_{a,b}}} \!\!\!\!\!\! {{{s}_{k}}(x,y)}} +|{{I}_{a}}|\times \!\!\!\!\!\! \sum\limits_{(y,z)\in ({{I}_{b}}\times {{I}_{c}})-{{M}_{b,c}}} \!\!\!\!\!\! {{{s}_{k}}(y,z)} \\ -|{{I}_{b}}|\times && \underbrace{\sum\limits_{x\in {{I}_{a}}}{\sum\limits_{z\in {{I}_{c}}-\{{{z}_{x}}\}} \!\!\!\!\!\! {{{s}_{k}}(x,z)}}}_{=\sum\limits_{(x,z)\in ({{I}_{a}}\times {{I}_{c}})-{{M}_{a,c}}} \!\!\!\!\!\! {{{s}_{k}}(x,z)}} \le |{{I}_{a}}|\times \left( |{{I}_{c}}|-1 \right)\times |{{I}_{b}}| \end{array} $$

Since $\bigcup \limits _{x\in {{I}_{a}}}{\{(x,{{y}_{x}})\}}={{M}_{a,b}}$ and $\bigcup \limits _{x\in {{I}_{a}}}{\{(x,{{z}_{x}})\}}={{M}_{a,c}}$, we divide both sides of the inequality by $(|{{I}_{a}}|\times \left (|{{I}_{c}}|-1 \right )\times |{{I}_{b}}|)$ to get LHS of(16) ≤ 1. □

Example 6

Recall the graph G in Figure 1, and three node-pairs (1,2),(2,3),(3,1) in G. For each pair (e.g., (1,2)), all the RoleSim* similarities of its in-neighboring pairs are tabularised as a grid (e.g., I₁ × I₂) in Figure 8, respectively. The green cells in each grid (e.g.,I₁ × I₂) correspond to the similarities over the maximum bipartite matching (e.g.,M_1,2); and the remaining cells in orange denote the similarities out of the bipartite matching (i.e., in I₁ × I₂ − M_1,2). Lemma 1 indicates that the similarity values in the green cells satisfy

Fig. 8

An illustrative example of Lemmas 1 and 2. The similarity grids for the in-neighbouring pairs of three node-pairs (1,2),(1,3),(2,3) in Figure 1 are visualised, respectively, to picturise RoleSim* triangular inequality

Similarly, Lemma 2 implies that the similarity values in the orange cells satisfy

Leveraging Lemmas 1 and 2, we are now ready to show the sum-transitivity of the RoleSim* similarity distance, which is the main result in this subsection:

Theorem 8 (RoleSim* Triangle Inequality)

We denote by d(a,b) := 1 − s(a,b) the closeness between nodes a and b. Then, for any three nodes a,b,c in a graph, the following triangle inequality holds, i.e.,

$$ d(a,b) + d(b,c) \ge d(a,c) $$

(17)

Proof

By the definition of d(a,b) := 1 − s(a,b), based on the fact that

$$ \begin{array}{@{}rcl@{}} d(a,b) + d(b,c) \ge d(a,c) \quad & \Leftrightarrow & \quad 1-s(a,b)+1-s(b,c)\ge 1-s(a,c) \\ & \Leftrightarrow & \quad s(a,b)+s(b,c)-s(a,c)\le 1 \end{array} $$

(18)

in what follows we will prove (18) holds by induction on k. For k = 0, by virtue of (3), it is apparent that

$$ s_{0}(a,b)+s_{0}(b,c)-s_{0}(a,c) = 1 + 1 - 1 = 1 \le 1. $$

For k > 0, we assume that s_k(a,b) + s_k(b,c) − s_k(a,c) ≤ 1 holds, and will prove that s_k+ 1(a,b) + s_k+ 1(b,c) − s_k+ 1(a,c) ≤ 1 holds.

Let P₁ and P₂ be left-hand side (LHS) of (12) and (16), respectively. According to Lemmas 1 and 2, it follows from P₁ ≤ 1 and P₂ ≤ 1 that

$$ \begin{array}{@{}rcl@{}} {{s}_{k+1}}(a,b)+{{s}_{k+1}}(b,c)-{{s}_{k+1}}(a,c) & =&\beta (\lambda P_{1} +(1-\lambda ) P_{2})+(1-\beta ) \\ & \le& \beta (\lambda +(1-\lambda ) )+(1-\beta ) \le 1 \end{array} $$

□

7 Scaling RoleSim* search using triangle inequality and partitioning

RoleSim* based similarity search can be also scaled via pruning using the triangular inequality property. With some pre-computation, one can prune the node-pairs that need not be evaluated and eliminate nodes from the candidate list to produce a top-k similar nodes rank list with less computation. We first discuss a strategy for retrieving approximate node-pair results based on graph partitioning. We then discuss exact single-source computation to obtain the most similar nodes to a query q, by indexing based on the distance to some chosen keys.

First, we consider a simple graph partitioning-based strategy, where graph G is partitioned using a vertex separator method to produce parts of roughly equal sizes. We refer to the set of vertex separators (also called vertex cut or separating set) as V_S. Nodes in V_S are the nodes that, when removed from G, separate it into its partitions. For our purposes, we include the set of nodes V_S with their corresponding edge connections into each of the partitions. That is, nodes in the V_S are the only nodes that are present in every subgraph constructed via this partitioning approach.

Example 7

Consider the digraph G in Figure 9a, where a 2-way partitioning has been performed resulting in vertex separators V_S = {3,7}. Subgraphs G₁ and G₂ are constructed such that $V_{G_1} = \{1,2,3,7\}$ and $V_{G_2} = \{3,4,5,6,7\}$. Using our single-source approach, all pairs of similarities from nodes in V_S to nodes in G can be pre-computed. Given a decay factor β = 0.8, and relative weight λ = 0.7, the exact RoleSim* similarities are computed (after k iterations) and cached for all s(v,∗) where v ∈ V_S. Now, for node-pair (2,1), the exact similarity score of s(2,1) from G₁ may be approximately computed as s_P(2,1) where the pre-computed value of s(3,7) is used in every iteration and only the pruned graph G₁ is considered. The similarity score s_PA(2,1) also uses the pre-computed s(3,7), but also allows access to neighboring nodes if they are present in G₂. As seen from Figure 9b and c, s_PA(2,1) is more accurate but less efficient due to accessing a larger graph.

Fig. 9

Approximate RoleSim* node-pair similarity retrieval that caches the similarities between vertex separators to all nodes and uses triangle inequality to compute approximate results for node-pairs (2,3) (case 1), (2,1) (case 2), (2,4) (case 3), where two partitions are encircled in red and blue respectively

Consider a query node q. To compute its similarity to any node n in G, there are three different cases:

• 1. One or both nodes are vertex separators, i.e., q ∈ V_S or n ∈ V_S: this means an exact value for s(q,n) is already pre-computed

• 2. Both nodes are in the same partition, say q,n ∈ G₁: this means an approximate value for s(q,n) can be computed considering G₁ as the input graph and discarding all nodes/edges from G₂

• 3. Both nodes are in different partitions, say q ∈ G₁ and n ∈ G₂: this means an approximate (lower bound) value for s(q,n) can be directly computed from the pre-computed exact values of s(v,∗) by making use of the triangle inequality property of RoleSim*

While case 1 returns the exact value, case 2 and case 3 lead to approximate results. This is depicted in Figure 9d, where numerous additional similarity computations (Figure 9e) are avoided by retrieving the values stored for nodes in V_S and using these to compute approximate results. In case 2 when G is pruned into G₁, the nodes/edges connections that are discarded no longer contribute to the similarity computation during the RoleSim* traversals, leading to inexact results. The case 3, considering q ∈ G₁ and n ∈ G₂ and pre-computed exact values of s(v,∗), is explained in further detail:

Using triangle inequality (18), we know that ∀v ∈ V_S:

$$ s(q, n) \geq s(q, v) + s(v, n) - 1 $$

Hence, using the pre-computed values s(v,∗), we know that s(q,n) must have its lower bound as the largest of these values, or:

$$ s(q, n) \geq \max_{\forall v \in V_{S}}(s(q, v) + s(v, n) - 1) $$

This can be extended to k-way partitioning. The vertex separator set is taken as one end node of each of the edge cuts in any k-way partitioning scheme, and included into each of the subgraphs.

Next, we discuss the challenge of returning an exact solution for the most similar nodes to a query q. The vertex separator set V_S is taken as a set of keys whose similarities to all nodes are pre-computed. From the triangle inequality, we know that:

$$ d(q,n) \geq |d(v,n)-d(q,v)| $$

(19)

Hence, a lower bound may be obtained on d(q,n), by computing:

$$ d(q,n) \geq \max_{v \in V_{S}} |d(v,n)-d(q,v)| $$

(20)

Given a threshold $s_{\min \limits }$, we want to find all nodes n_i such that $s(q,n_i) \geq s_{\min \limits }$. That is, d(q,n_i) ≤ ξ where $\xi = 1 - s_{\min \limits }$. The lower bounds d(q,n_i) for all nodes n_i are given by (20). Any lower bound greater than ξ allows the node n_i to be pruned from the candidate list. We denote the resulting candidate set as V_k. In large graphs, with careful partitioning to select a small number of vertex separators (|V_k|≪|V |), the number of distance computations is substantially reduced.

One can use this approach to prune partitions while identifying the top-k similar nodes to query q. Consider subgraphs G_j obtained by partitioning G, each containing a single vertex separator v. Using pre-computed values for d(v,∗), (19) gives the lower bounds of d(q,n_i) for $n_i \in V_{G_j}$ (j = 1,⋯ ,N_P respectively for each of the N_P partitions). The minimum of all these distances within a partition gives a lower bound value that helps to index the partitions:

$$ d(q,n_{i}) \geq \min_{n_{i} \in V_{G_{j}}} |d(v,n_{i})-d(q,v)| $$

Let us denote these lower bounds as $\xi _{G_j}$ for each subgraph G_j. Without loss of generality, suppose $\xi _{G_1} > \xi _{G_2}$ for a 2-way partitioning of G. Thus, every node in G₁ is necessarily at least $\xi _{G_1}$ distance away from q. We first compute exact distances for all nodes in G₂. If k such nodes all have a distance to q that is smaller than $\xi _{G_1}$, then nodes of G₁ need not be considered, and the resulting top-k can be directly returned. If not, that is if any nodes of G₂ are at a distance higher than the lower bound of the next partition (here, G₁), then nodes of G₁ must be processed. These nodes are then inserted into the top-k ranking based on the computed distances. A similar process continues through the ordered set of $\xi _{G_j}$ values for multi-way partitioned data.

8 Experimental evaluation

8.1 Experimental settings

Datasets.

We use 8 real datasets with different scales, as illustrated below:

	Datasets	(Abbr.)	|V |	|E|	|E|/|V |	Type
small	DBLP	(DBLP)	2,372	7,106	2.99	Undirected
	Amazon	(AMZ)	5,086	8,970	1.76	Directed
	HEP-Citation	(CIT)	34,546	421,578	12.20	Directed
medium	P2P-Gnutella	(P2P)	62,586	147,892	2.36	Directed
	Email-EuAll	(EML)	265,214	420,045	1.58	Directed
	Web-Google	(WEB)	875,713	5,105,039	5.82	Directed
large	YouTube	(YOU)	1,134,890	2,987,624	2.63	Undirected
	LiveJournal	(LJ)	4,847,571	68,993,773	14.23	Directed

• DBLP. A collaboration (undirected) graph taken from DBLP bibliography.⁴ We extract a co-authorship subgraph from six top conferences in computer science (SIGMOD, VLDB, PODS, KDD, SIGIR, ICDE) during 2018–2020. If two authors (nodes) co-authored a paper, there is an edge between them.

• Amazon. A co-purchasing graph crawled from Customers Who Bought This Item Also Bought feature of Amazon⁵. Each node is a product, and edge i → j means that product j appears in the frequent co-purchasing list of i.

• HEP-Citation. A citation digraph from arXiv scholarly physics articles. In this graph, nodes represent papers, and there is a directed edge from paper u to paper v if paper u cites paper v.

• P2P-Gnutella. A file sharing graph from Gnutella peer-to-peer network. In this graph, nodes represent hosts, and each edge denotes the connection from one host to another in the Gnutella network.

• Email-EuAll. A digraph constructed from emails of a research institute. Each node represents an email address, and there is a link from node u to v if at least one email is sent from u to v.

• Web-Google. A Google web digraph from SNAP⁶ network repository. In this digraph, nodes represent web pages, which are connected by directed edges that represent the hyperlinks from one web page to another.

• YouTube. A friendship (undirected) graph from YouTube video sharing website, which is an online social network. In this digraph, nodes denote users, and edges are the friendship relation between them.

• LiveJournal. A large friendship graph from LiveJournal community. This is an online social network, in which nodes are users, and each edge i → j is a recommendation of user j from user i.

All experiments are conducted on a PC with Intel Core i7-10510U 2.30GHz CPU and 16GB RAM, using Windows 10. Each experiment is repeated 5 times and the average is reported.

Compared Algorithms

We implement the following algorithms in VC++:

Models	(Abbr.)	Description
RoleSim*	(RS*)	our proposed RoleSim* model in Algorithm 1.
Single-Src RS*	(SSRS*)	our proposed single-source RoleSim* model in Algorithm 2.
SimRank	(SR)	a pairwise similarity model proposed by Jeh and Widom [7].
MatchSim	(MS)	a model relying on the matched neighbors of node-pairs [17].
RoleSim	(RS)	a model that ensures the automorphic equivalence of nodes [9].
RoleSim++	(RS++)	an enhanced RoleSim that considers in- and out-neighbors [25].
CentSim	(CS)	a model that compares the centrality of node-pairs [14].

Parameters

We use the following parameters as default: (a) damping factor β = 0.8, (b) relative weight λ = 0.7, (c) total number of iterations K = 5.

Unsupervised Semantic Evaluation

We design an unsupervised evaluation setting to quantify the effectiveness of the similarity measures. We use self-similarity as the ground truth and study the effect of sampling the immediate neighborhood of a query node on similarity scores in RoleSim* compared with SimRank and RoleSim.

Our evaluation is inspired by the problem of determining duplicate nodes in a network simply by examining their neighborhoods for similar patterns. In many applications, the underlying network contains duplicate entities with noisy, incomplete, and partially overlapping information, such as in a social network that has been scraped from multiple sources. Similarity of duplicate nodes is expected to be high. We consider duplicate entities as separate nodes, where each duplicate has some sampling of the total set of neighboring edges available to the node. For example, in a co-purchasing product graph (AMZ), duplicates may exist when merging multiple e-commerce sources, or when identical products are sold by different sellers. This indicates that each of these duplicate products were frequently purchased along with certain other products as they share some common neighbors. Similarly, incorrectly spelled author names or multiple sources for a paper can lead to duplicates in co-authorship and citation networks (DBLP, CIT).

Consider a single query node q. In our experiments, we create a node q^′ and add it to the graph. We connect $q^{\prime }$ to some proportion (η) of the total number of neighbors of q, and hereby refer to $q^{\prime }$ as the “sampled clone”. The similarity scores of q to all other points in the graph are computed using SimRank, RoleSim, and RoleSim*. We evaluate how much the relative similarities are preserved when different measures are used. First, we vary η for $q^{\prime }$ with step size 0.25 (and ensuring no orphaned nodes) while varying λ = 0.0,0.3,0.5,0.7,1.0 for RoleSim* and compare the resulting similarity scores. In a similar experiment, we vary both η (for q) as well as $\eta ^{\prime }$ (for $q^{\prime }$) each with step size 0.25, resulting in some overlap of neighborhoods as the values of η and $\eta ^{\prime }$ grow towards 1. These results are aggregated over 20 queries on DBLP and AMZ graphs respectively, where query nodes are chosen as having high degree of neighbors.

8.2 Experimental results

Semantic Accuracy

We first count the number of queries where the sampled clone $q^{\prime }$ appears in the top-k (k = 1,5,10) similar nodes to query q for RoleSim*. Intuitively, this studies how much structural information is gleaned about a query node. Figure 10a presents the number of such queries out of 20 on the undirected DBLP graph, considering top-5 similarity scores. Other top-k plots are omitted, but show that with increasing k for a given sampling proportion there are more such queries even at lower λ.

Fig. 10

Effect of Sampling Ratio (η) & Weight (λ) on Ranking Quality (DBLP)

Next, we test the impact of sampling η and λ on ranking quality in RoleSim*. We plot the average ranking quality (normalized discounted cumulative gain (nDCG)), considering top-100 similar nodes of the sampled clone and comparing this to the baseline original query. We observe that the trend (with respect to η) seen in Figures 10b and 11b for λ = 1 resembles that for RoleSim, and the trend for λ = 0.5 is close to that for SimRank.

We further consider a fixed value of λ = 0.7 and confirm that the RoleSim* has higher ranking quality compared to SimRank and RoleSim, with respect to the average nDCG. Figure 10c with undirected DBLP graph shows that RoleSim* produces a more consistent nDCG even with small η. For the directed AMZ graph in Figure 11c too, RoleSim shows significant improvement at lower sampling, and the performance of SimRank is negatively affected throughout, while RoleSim* remains stable.

Fig. 11

Effect of Sampling Ratio (η) & Weight (λ) on Ranking Quality (AMZ)

Finally, we also check the results obtained on varying the sampling of both q and $q^{\prime }$ together (sampling η and $\eta ^{\prime }$ neighboring edges respectively). For the resulting top-k similarity lists, we count the number of queries (out of 100) for which clone $q^{\prime }$ is present in top-10 results for q (plots are omitted here). This provides an estimate for the number of duplicate entities that can be correctly identified. We note that RoleSim and RoleSim* are both heavily impacted when there is a large mismatch in the sampled neighborhood sizes. Specifically, the exact nature of the neighboring nodes themselves appears less important compared to the relative structure of connectivity patterns with the neighborhood. Despite random samples of neighborhoods, the results peak only when the neighborhood sizes are close to each other (i.e.,η and $\eta ^{\prime }$ are equal).

Overall, nDCG scores of RoleSim* are superior to RoleSim, while SimRank performs poorly when sampling rates are low. These results together indicate that for the challenge of identifying duplicate entities. RoleSim* is best suited to correctly identify a match when presented with a noisy sample of edge connections from the duplicate node. In particular, taking only a small sample of edges from both the duplicate and the original nodes produces best matching results.

Qualitative Case Study

Table 2 compares the similarity ranking results from three algorithms (SR, RS and RS*) for retrieving top-10 most similar authors w.r.t. query “Philip S. Yu” on DBLP. From the results, we see that the top rankings of RS* are similar to RS, highlighting its capability to effectively capture automorphic equivalent neighboring information. For instance, “Jure Leskovec” is top-ranked in RS* list. This is reasonable because he and “Philip S. Yu” have similar roles - they are both Professors in Computer Science with close research expertise (e.g., knowledge discovery, recommender systems, commonsense reasoning). However, the rankings of RS* are different from those of RS. For example, “Jure Leskovec” is ranked 350^th by SR, but 4^th by RS* and RS. This is because SimRank can only capture connected paths between two authors while ignoring their automorphic equivalent structure. “Jure Leskovec” has rare collaborations with “Philip S. Yu”, both direct and indirect, thus leading to a low SimRank score.

Table 2 Similarity rankings for “Philip S. Yu” on DBLP co-authorships data

To evaluate RS* further, we choose two different values for λ ∈{0.6,0.8} to show how RS* ranking results are perturbed w.r.t.λ. From the results, we notice that, when λ is varied from 0.6 to 0.8, nodes with small SR scores (e.g., “Jure Leskovec”) exhibit a stable position in RS* ranking, whereas nodes having higher SR scores (e.g., “Huan Liu”) have a substantial change. This conforms with our intuition because “Huan Liu”’s collaboration with “Philip S. Yu” is closer than “Jure Leskovec”’s, and RS* is able to capture both connectivity and automorphic equivalence of two authors using a balanced weight λ. Thus, compared with “Jure Leskovec”, “Huan Liu” who has higher SimRank value with “Philip S. Yu” is more sensitive to λ change, as expected.

Computational Time

The second set of experiments is evaluating the computational time of seven algorithms (SSRS*, RS*, RS, MS, RS++, CS, SR) on various real-life datasets, including both medium graphs (e.g., CIT, P2P, EML) and large graphs (e.g.,WEB, YOU, LJ).

Figure 12 compares the computational time of SSRS* with other competitors (e.g., RS, MS, RS++, CS, SR) for single-source queries {s(∗,q)}. On each dataset, we randomly select 100 nodes as queries, according to their PageRank values, to guarantee the selected queries cover a possible range of the most important and moderately important nodes. We take the average time for computing single-source {s(∗,q)} over all the queries. From the results, we observe that (1) on all datasets, SSRS* is consistently faster than the other algorithms, highlighting the effectiveness of our caching techniques that eliminates a significant number of unnecessary recomputations in DFS backtracking. In comparison, RS*, RS, MS, and RS++ must store all-pairs similarity values of the last iteration for iteratively computing the scores of the next iterations. (2) On large datasets (e.g., WEB, YOU, LJ), SSRS* and CS scale well, whereas the other algorithms crash due to the explosion of the memory that is required for storing all-pairs similarity information for iterative computations. In contrast, SSRS* retrieves only a small portion of required pairwise similarity information per level on an as-needed basis. CS is also scalable on sizable graphs since it simply assesses pairwise similarities one by one through aggregating node centrality values, thus leading to low computation time. However, SSRS* is consistently 5–8 times faster than CS due to our unordered hashing techniques for minimising unnecessary recomputations. (3) On small datasets (e.g., DBLP, AMZ, CIT) where all the algorithms survive, RS* has comparable computational time to RS and MS. This implies that RS* achieves high accuracy without sacrificing running speed. In addition, RS*, RS, and MS are faster than RS++. This is because RS++ needs to find two maximum bipartite matchings for both in- and out-neighboring pairs, as opposed to RS* that involves the computation of only one matching. SR is slightly faster than RS*. This is consistent with our analysis as SR simply takes the average of all similarities of the in-neighboring pairs without the need to find the maximum bipartite matching.

Fig. 12

CPU Time Comparison on 8 Real Datasets

Figure 13a and b show the effect of iteration number k and threshold δ on the running time of RS* on DBLP and AMZ, respectively. For each dataset, we vary δ from 0 to 0.05. When δ = 0, it reduces to RS* algorithm. From the results on both datasets, we discern that, for each fixed δ, the running time of threshold-based RS* increases as k grows. When δ becomes larger, the growth rate of RS* time tends to be sublinear. For example, when δ = 0.05 on DBLP, only after k = 5 iterations, the increasing time of threshold-based RS* has leveled off. In contrast, when δ = 0.01, the time becomes steady after k = 8 iterations. The reason is that a higher setting of threshold δ implies a larger number of pairs to be pruned per iteration, thus leading to the growth rate of the running time decreasing in an earlier stage during iterations.

Fig. 13

CPU Time Comparison for Different Threshold-Based RS*

Figure 14a and b show the influence of different threshold values (δ) and the number of iterations (k) on the computational time of SSRS* on EML and YOU, respectively. We vary δ from 0.01 to 0.1 for each dataset, and k from 3 to 9 and 6, respectively for EML and YOU. From the results, we notice that (1) for any fixed δ, the running time of threshold-based SSRS* increases more mildly than that of SSRS* as k grows. For instance, when δ = 0.05 on EML, the threshold-based SSRS* is 2.9 (resp. 3.14) times faster than SSRS* at iteration k = 7 (resp.k = 9). This is because the similarity values decrease with the growing number of iterations. Thus, a larger number of node-pairs with smaller similarity values may appear more often when k is larger, thereby having a higher chance to be pruned, as expected. The similar trend holds on YOU. (2) At each iteration k, increasing the threshold δ will enable a moderate reduction in the running time of the threshold-based SSRS*. For example, for k = 9 on EML, when δ = 0.05 (resp.δ = 0.1), the threshold-based SSRS* is 3.14 (resp. 3.41) times faster than SSRS*. The reason is that higher settings of δ will result in a larger number of pairs to be pruned per iteration, which agrees well with our basic intuition.

Fig. 14

CPU Time Comparison for Different Threshold-Based SSRS*

Memory Usage

We next compare the memory usage of SSRS* with other competitors on real datasets. The results are reported in Figure 15. It is discerned that SSRS* and CS are the only algorithms that scale well on all the datasets, including billion-edge graphs (e.g., YOU and LJ), as opposed to other algorithms that crash on any sizable graphs due to memory explosion. In addition, even on small graphs, where all the algorithms survive, the memory required by SSRS* is one order of magnitude smaller than others, except for the CS on DBLP, AMZ,CIT datasets. This is because RS*, RS, MS, RS++ need to memoise the entire similarity matrix of an iteration to compute similarities at the next iteration, thereby leading to quadratic memory. In comparison, SSRS* selects only the “important” pairs for memoization to eliminate unnecessary recomputations in DFS backtracking.

Fig. 15

Memory space comparison on real datasets

Effect of Threshold δ on RS* Accuracy

Figure 16a and b show the influence of threshold δ on RS* accuracy over real datasets (DBLP and AMZ). The accuracy is evaluated using three ranking measures (Spearman, Kendall, nDCG). We randomly sample 100 queries from each dataset, and vary threshold δ from 0.01 to 0.05. For each δ, we compute single-source threshold based RS* similarities $\{s_k^{\delta }(*,q)\}$ w.r.t. each query q. Choosing non-threshold based RS* similarities {s_k(∗,q)} as the baseline, we evaluate the average value of Spearman, Kendall, and nDCG, respectively, for each threshold based RS* over 100 queries on each dataset. We notice that, on each dataset, all the threshold based RS* consistently achieve > 98% accuracy by each ranking measure. For top-100 results on both datasets, the similarity rankings attain > 99% nDCGs on average. These imply that the accuracy compromised by the threshold based RS* is negligibly small for fast speed. Moreover, when δ increases from 0.01 to 0.05, the accuracy decreases slightly for each ranking measure because large threshold may prune a large number of node-pairs per iteration. This agrees well with the pruning table in Figure 16c, where large δ implies more pairs are eliminated at each iteration.

Fig. 16

Accuracy comparison for different threshold-based RS*

Figure 17a and b illustrate the influence of threshold δ on SSRS* accuracy over EML and YOU datasets. The accuracy evaluated using Spearman, Kendall and nDCG ranking measures on 100 randomly selected queries from each dataset. To compare the effect of threshold value on accuracy we select three δ = 0.01, δ = 0.05 and δ = 0.1 values. For each δ value, we compute SSRS* similarities $\{s_k^{\delta }(*,q)\}$ w.r.t. each query q by choosing non-threshold-based SSRS* similarities {s_k(∗,q)} as the baseline. We evaluate the average value of Spearman, Kendall, and nDCG, respectively, for each threshold-based SSRS* over 100 queries and on each dataset. We notice that, (1) on each dataset, threshold-based SSRS* with δ = 0.01 and δ = 0.05 achieve > 99% accuracy by Spearman and Kendall ranking measures, while for δ = 0.1 the ranking accuracy slightly decreases to > 96%, this is predictable due to the high number of pruned pairs that caused by higher δ value, which is consistent with the pruning table in Figure 16c. (2) For top-100 results on both datasets, the similarity ranking results reach> 99% nDCGs on average. These results point out that the threshold-based SSRS* provides high computation speed with an insignificant decrease in accuracy.

Fig. 17

Accuracy comparison for different threshold-based SSRS*

Effect of Partitioning on SSRS*

We present an illustrative partitioning scheme (using the triangle inequality property) that may be applied for approximate SSRS* computation. The accuracy (nDCG) and efficiency over real datasets (DBLP and AMZ) are evaluated by randomly sampling 100 queries from each dataset. With varying number of iterations k, we compute single-source RS* similarities {s_k(∗,q)} w.r.t. each query q. Choosing SSRS* similarities {s_k(∗,q)} as the baseline, we evaluate the average value of nDCG for both SSRS*-P and SSRS*-PA over 100 queries on each dataset. For both approaches, METIS [11] is used to generate 2-way partitioning of the graph using the vertex separator method. Similarity scores are pre-computed from these vertex separator nodes to all nodes, and these cached values are retrieved during single-source RS* computations. SSRS*-P denotes an approach where only the pruned subgraph is considered for similarity computation, while SSRS*-PA denotes an approach where access to neighboring nodes in other partitions is allowed during the similarity computation. Figures 18a and 19a indicate that, on these datasets, SSRS*-P achieves close to 85% accuracy in terms of nDCG for top-100 results. SSRS*-PA is more accurate, however it incurs much higher computational time due to more edge connections being taken into consideration. As seen from Figures 18b and 19b, a partitioning approach like SSRS*-P may offer a more scalable computation of approximate similarity scores even for large number of iterations.

Fig. 18

Accuracy and CPU time comparison for partitioned SSRS* (DBLP)

Fig. 19

Accuracy and CPU time comparison for partitioned SSRS* (AMZ)

Iterative Error.

Finally, we evaluate the effects of number of iterations k on the iterative error of RS*. The error is measured by difference 𝜖_k between k-th iterative score s_k(∗,∗) and exact one s(∗,∗). We only report the results for a pair of nodes on DBLP since the trends for other pairs and on other datasets are similar. For any pair of nodes on DBLP, we fix damping factor β, and vary k from 1 to 15.

Figure 20 depicts how k-th iterative error 𝜖_k changes with k. It is discerned that, for any given damping factor β, 𝜖_k exponentially decreases to 0 as k grows. The larger damping factor β will cause a shift outward in the accuracy curve, thereby exhibiting the slower convergence rate of RoleSim* iterations. In addition, at each iteration k, it is noticed that small settings of damping factor β will lead to small iterative error of RoleSim*. These agree well with our theoretical bound $k = \lceil \log _{\beta } \epsilon _k \rceil$ in Theorem 4 for RoleSim* accuracy analysis.

Fig. 20

Effect of (k,β) on 𝜖_k

The actual and the estimated error bound value for β = 0.6 and β = 0.8 per iteration are illustrated in Table 3, which shows that, for each iteration, the computed actual error bounds are completely compatible with the theoretical estimated error bounds.

Table 3 Actual & Estimated Error

9 Conclusions

We propose RoleSim*, a novel similarity model that guarantees automorphic equivalence while considering neighboring similarity information beyond automorphically equivalent sets, thereby achieving better performance than both SimRank and RoleSim. We prove the existence and uniqueness of the RoleSim* solution, show that iteratively computing RoleSim* is bounded, and induce a RoleSim* distance obeying sum-transitivity of similarity scores. We also propose a threshold-based RoleSim* model to prune a number of pairs with tiny similarity values, which enables a further speedup with guaranteed accuracy. Moreover, we propose an efficient single-source Rolesim* algorithm that scales well on large graphs with billions of edges. Taking advantage of the “triangular inequality” property of RoleSim*, we also introduce a partitioning-based strategy to scale RoleSim* on large graphs. Finally, we evaluate our model on different real datasets to demonstrate its superior ranking quality, fast speed, and high scalability against state-of-the-art competitors.