Abstract
This paper derives and optimizes the throughput of NOMA with nonlinear energy harvesting. The Base Station (BS) harvests energy from the received Radio Frequency signal. Then, the BS uses the nonlinear harvested power to diffuse packets to N users. We suggest to optimize harvesting time and the powers of users to optimize the data rate. The optimization of NOMA powers and the harvesting process were not yet performed with a non linear energy harvesting model. The study is performed for Rayleigh channels in the presence of nonlinear energy harvesting model. Furthermore, the theoretical results were confirmed using MATLAB computer simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Literature Review
In Orthogonal Multiple Access (OMA), transmission to N users is performed over N different bands with width B/N where B is the total available band. Each user obtains a maximum throughput of \(log_2(K)/N\) where K is the size of modulation. NOMA has been suggested to maximize the total throughput [1,2,3,4] since transmission to all users is performed over the available band B. Powers allocated to users should be optimized to reduce the effects of interference between users [5,6,7,8]. Weak user demodulates only its signal while strong users detects the weak user signal. In fact, the weak user signal is sent with a larger amplitude. Then, strong user subtracts the weak user signal to detect its signal [8]. NOMA has been deployed in Cognitive Radio Networks to transmit data to primary or secondary users [9,10,11,12]. Transmission to secondary users using NOMA can be performed when primary users are idle. Opportunistic spectrum access allows to benefit from unused bands [9,10,11,12]. Besides, NOMA transmission to primary or secondary users can be performed with adaptive power so that the interference is constrained to a given maximum value [9,10,11,12].
NOMA with power harvesting has been studied [13,14,15]. The base station harvests power from RF signals [13,14,15,16,17]. NOMA with a linear energy harvesting model was studied in [18]. Sum rate maximization of NOMA was suggested in [19]. Analysis of the maximum power harvesting capacity was derived in [20] assuming a linear energy harvesting model. The security of NOMA using multiple antennas was studied in [21]. A linear energy harvesting model has been considered in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. The Furthermore, harvesting time has not been yet optimized. We study the throughput of NOMA with a non linear energy harvesting model. Powers of users and harvesting time are optimized to enhance the offered data rate this is the main contribution of the paper.
NOMA with two users is considered in Sect. 2. Section 3 generalize the model to N users. The results are shown in Sect. 4. Section 5 summarizes the results.
2 NOMA with Two Users
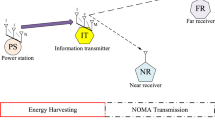
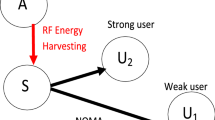
Figure 1 shows the network model with a Base Station and two users \(U_1\) and \(U_2\). \(U_1\) is the weak user and \(U_2\) is the strong user such that: \(\lambda _1=E(|h_1|^2)<\lambda _2=E(|h_2|^2)\) where \(h_i\) is channel from BS to \(U_i\). In the first time duration, BS harvests power from the signal of A. Powee harvesting is done over \(\beta F\) second where \(0<\beta <1\) gives the harvesting time and F is frame length. The harvested energy is [17]
where \(E_A\) is the symbol energy of A, \(P_A=\frac{E_A}{T_s}\), \(T_s\) is the symbol duration, \(\alpha \) is a proportional coefficient, \(L_0=\frac{F}{T_s}\) and \(h_{ABS}\) is channel from A to BS.
The complexity of non linear energy harvesting is \(\alpha L_0\) complex multiplications.
The non linear harvested energy is [17]
where [27]
Typical values of parameters are \(N=0.02\), \(C=1500\) and \(B=0.002\) [17].
The CDF of \(E_{nonlinear}=\Psi (E)\) is computed as
where \(\lambda _{ABS}=E(|h_{ABS}|^2)\)
Let
The CDF of \(X_i\) is
where \(\lambda _i=E(|h_i|^2)\).
In the second time duration, during \((1-\beta )F\) seconds, the BS transmits jointly \(s_1\) and \(s_2\) of users \(U_1\) and \(U_2\): \(\sqrt{p_1}s_1+\sqrt{p_2}s_2\) where \(1>p_1>p_2>0\) are the powers allocated to users such that \(p_1>p_2\). The signal at \(U_i\) is
where \(n_i\) is Gaussian of variance \(N_0\).
Weak user \(U_1\) estimates \(s_1\) with SINR
where \(X_i\) is defined in (6).
The outage probability at \(U_1\) is
where \(p_{X_1}(y)\) is given in (7).
Strong user \(U_2\) detects symbol \(s_1\) since \(p_1>p_2\) with SINR
Then \(U_2\) subtracts \(s_1\) and estimates \(s_2\) with SNR
There is no outage at \(U_2\) if both SNR \(\gamma _2^{2\rightarrow 2}\) and SINR \(\gamma _2^{2\rightarrow 1}\) are greater than y:
where \(p_{X_2}(y)\) is given in (7).
The BLock Error Probability (BLEP) at \(U_i\) is given by [22]
where
blep(y) is
Q is packet size and S(y) is [23]
and K is the constellation size of K Quadrature Amplitude Modulation (K-QAM).
The data rate at \(U_i\) is computed as
Therefore, the total data rate is
Harvesting duration \(\beta \) and powers \(p_1\) and \(p_2\) are optimized to maximize the total throughput
3 NOMA with N Users
Power harvesting is performed in the first time duration. In the second time duration, BS sends \(\sum _{i=1}^N\sqrt{p_i}s_i\). The signal at \(U_q\) is
As sown in Fig. 2, \(U_q\) is the \((N-q+1)\) strongest user such that \(\lambda _1<\lambda _2<...<\lambda _N\) where \(\lambda _i=E(|h_i|^2)\). More power is allocated to \(U_1\): \(1>p_1>p_2>...>p_N>0\). User \(U_q\) starts by detecting \(s_1\) with SINR
Then \(U_q\) performs subtracts the signal of \(U_1\) and demodulates \(s_2\) and the SINR is
Similarly, \(U_q\) will detect \(s_m\) for \(m=1,2,...,q\) with SINR
We deduce
The BLEP and throughput are computed using (14) and (18). The total throughput is computed as
Harvesting duration \(\beta \) and powers \(p_1\) and \(p_2\) are given by
4 Results and Discussion
Figures 3, 4, 5, 6 depict the BLEP and throughput at \(U_1\) and \(U_2\) for harvesting time \(\beta =0.5\). There are two users located at 1 and 1.2 from the base station. We observe that the throughput increases at high SNR when 16QAM modulation is used with respect to Quadrature Phase Shift Keying (QPSK). Besides, the throughput at strong user is larger than that at weak user.
In Fig. 7, the total throughput is shown for 16QAM and QPSK modulations. Optimal Power allocation (OP) increases the total throughput. It is crucial to optimize harvesting time \(\beta \) to maximize data rates. The throughput is 8 bit/s/Hz at high SNR for 16QAM and when the harvesting process is optimized. However, the throughput is only 4 bit/s/Hz as obtained in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].
In Fig. 8, the throughput is shown for 16QAM modulations for 3 users at distances 1, 1.1 and 1.2 from the BS. We see that OP and optimal harvesting time allow to increase data rates. Optimal powers and optimal \(\beta \) offer a throughput equal to 12 bit/s/Hz while the throughput is less than 6 bit/s/Hz when \(\beta \) is not optimized as suggested in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Performance enhancement with respect to [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] is about 22 dB.
5 Conclusion
We have optimized the power harvesting process for NOMA systems. We used a realistic nonlinear power harvesting model and optimized the energy harvesting time to maximize the throughput. We obtained up to 8 dB gain by optimizing the power harvesting time and the results are valid for any network.
Data Availability
Data and material are not available.
Code Availability
Software application and custom code are non available.
References
Li, Q. C., Niu, H., Papathanassiou, A. T., & Wu, G. (2014). 5G network capacity: Key elements and technologies. IEEE Vehicular Technology Magazine, 9(1), 71–78.
Saito, Y., Benjebbour, A., Kishiyama, Y., & Nakamura, T. (2013). System-level performance evaluation of downlink non-orthogonal multiple access (NOMA), In Proc. IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Sep. 2013, pp. 611-615.
Ding, Z., Peng, M., & Poor, H. V. (2015). Cooperative non-orthogonal multiple access in 5G systems. IEEE Communications Letters, 19(8), 1462–1465.
Ding, Z., Dai, H., & Poor, H. V. (2016). Relay selection for cooperative NOMA. IEEE Communications Letters, 5(4), 416–419.
Men, J., & Ge, J. (2015). Non-orthogonal multiple access for multiple-antenna relaying networks. IEEE Communications Letters, 19(10), 1686–1689.
Niu, Y., Gao, C., Li, Y., Su, L., & Jin, D. (2016). Exploiting multi-hop relaying to overcome blockage in directional mmwave small cells. Journal of Communications and Networks, 18(3), 364–374.
Kim, J. B., & Lee, I. H. (2015). Non-orthogonal multiple access in coordinated direct and relay transmission. IEEE Communications Letters, 19(11), 2037–2040.
Zhong, C., & Zhang, Z. (2016). Non-orthogonal multiple access with co-operative full-duplex relaying. IEEE Communications Letters, 20(12), 2478–2481.
Liu, Y., Ding, Z., Elkashlan, M., & Yuan, J. (2016). Non-orthogonal multiple access in large-scale underlay cognitive radio networks. IEEE Transactions on Vehicular Technology, 65(12), 10152–10157.
Bhattacharjee, S., Acharya, T., & Bhattacharya, U. (2018). NOMA inspired multicasting in cognitive radio networks. IET Communications, 12(15), 1845–1853.
Liu, M., Song, T., & Gui, G. (2018). Deep cognitive perspective: Resource allocation for noma based heterogeneous IoT with imperfect SIC. IEEE Internet of Things Journal, 6(2), 2885–2894.
Xu, L., Zhou, Y., Wang, P., & Liu, W. (2018). Max-min resource allocation for video transmission in NOMA-based cognitive wireless networks. IEEE Transactions on Communications, 66(11), 5804–5813.
Sun, H., Zhou, F., Hu, R. Q., & Hanzo, L. (2019). Robust beamforming design in a NOMA cognitive radio network relying on SWIPT. IEEE Journal on Selected Areas in Communications, 37(1), 142–155.
Zhou, F., Chu, Z., Sun, H., & Leung, V.C.M. (2018). Resource allocation for secure MISO-NOMA cognitive radios relying on SWIPT, IEEE International Conference on Communications (ICC), pp. 1-6.
Liu, Y., Ding, Z., Elkashlan, M., & Poor, H.V. (2016) Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer, IEEE Journal on Selected Areas in CommunicationS, 34(4).
Varshney, L. (2008) Transporting information and energy simultaneously, In Proc. IEEE Int. Symp. Inf. Theory (ISIT), Toronto, Canada, pp. 1612–1616.
Li, Lihua, C., Rongting, J., Hui, & Su, X. (2019). Rate-energy tradeoff for SWIPT systems with multi-user interference channels under non-linear energy harvesting model, 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring).
Tran, H. Q. (2024). PSR versus TSR relaying protocols: Leveraging full-duplex DF and energy harvesting for SWIPT in NOMA Systems, Wireless Personal Communications, Published online March.
Noori Shirazim, M. B., & Zahabi, R. (2024). Sum-rate and energy efficiency optimization by novel relay selection in a NOMA-based cooperative network in the presence of interference, Wireless Personal Communications, Published online March.
Sainath, B. (2024). Estimation and analysis of maximum energy harvested in RF-EH wireless system over different fading channels, Wireless Personal Communications, Published online March.
Krishna, M., & Chunkath, Job. (2024). Privacy protection for NOMA systems with artificial noise and antenna diversity, Wireless Personal Communications, Published online March.
Xi, Y., Burr, A., Wei, J. B., & Grace, D. (2011). A general upper bound to evaluate packet error rate over quasi-static fading channels. Transactions on Wireless Communications, 10(5), 1373–1377.
Proakis, J. (2007). Digital communications (5th ed.). Mac Graw-Hill.
Funding
Open Access funding provided by the Qatar National Library. Open Access funding provided by the Qatar National Library.
Author information
Authors and Affiliations
Contributions
This is the contribution of Dr. N. Ben Halima
Corresponding author
Ethics declarations
Conflict of interest
There is no Conflict of interest for this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ben Halima, N. Non Orthogonal Multiple Access (NOMA) Using a Nonlinear Energy Harvesting Model. Wireless Pers Commun 135, 2165–2175 (2024). https://doi.org/10.1007/s11277-024-11129-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-024-11129-9