Embedded Nano Relay for Intra-Body Network-Based Molecular Communications

Abstract

We propose an embedded synthetic relay transport protein (RTP) approach for communication between the external environment (blood vessels) and internal targeted nanonetworks (cells/tissues) within the intra-body network. In fact, we designed a bioengineered relay protein-based facilitated diffusing to be an alternative protein in the case of biological transport proteins (such as protein channels, e.g. Pores) failing. The proposed approach is inspired by the traditional wireless communication system-based relay concept, in which embedded nanodevices known as donor, relay, and acceptor bionanomachine construct a molecular communication system. Fluorescence resonance energy transfer nanocommunications are used to connect the embedded bionanomachines, and the therapeutic drug is transferred in the form of exciton. The performance analysis of the proposed approach is evaluated in terms of channel capacity of RTP as function of intrinsic environmental parameters and the location of the relay between the donor, and acceptor bionanomachines. The numerical results show that the proposed approach improves channel capacity by 16.7% over previous work.

1 Introduction

The exchange of molecules between biological cells and the circulation system, or between biological entities of living organisms, can help the promising molecular communication (MC) paradigm to be implemented [1, 2]. Transport proteins, on the other hand, are proteins that transport messenger molecules (i.e. drugs) across membranes. The transmission process is carried out using two methods: facilitated diffusion (FD), which is based on a passive concentration gradient, and active transport, which is based on how a cell expends energy to move messenger molecules against a concentration gradient [3]. Passive diffusion occurs via a selective bipolar membrane (SBM) of small molecules such as O₂ and CO₂. However, polar and charge molecules are repelled by the SBM, resulting in the formation of certain proteins. These proteins are in charge of localizing channels and carriers that communicate polar and charge molecules via SBM. The channel (or Pores) protein, which can open and close channels in a cell's membrane, is one of the most important transport proteins. A good example of a transport protein is a process found in neuron systems known as voltage-gated ion channels, in which the channel opens in response to changes in the electrochemical potential of a membrane [4]. Another type of transport protein is the sodium–potassium pump, which changes its shape by using the energy of adenosine triphosphate (ATP) [5].

In general, proteins are required for the exchange and dissemination of information among biological entities, as well as for the survival of cells. Some studies have looked at how plasma pharmacokinetics, the structure and function of tumor vasculature, and the protein transport properties of the drug as it moves through micro-vessel walls and extravascular tissue affect drug distribution [6]. Because of this, transport proteins play critical roles in transferring polar molecules from one side of a high concentration gradient to another based on FD. Our current work focuses on the transport of drugs between intravascular and extravascular tissue as scenario of targeted drug delivery (TDD) systems. We consider a TDD scenario based on a molecular communication system with an embedded relay bionanomachine labeled with fluorescent molecules to deliver therapy drugs to the targeted tissues (cells). On the other hand, the deployment of the Internet of bio-nano things (IoBNT) paradigm as a remote control over the dissemination and exchange of information molecules via an embedded bionanomachines network is feasible for achieving important medical goals such as targeted drug delivery (TDD) systems and health care monitoring (HCM) applications [3, 7,8,9,10,11,12]. In addition, the molecular communication system is regarded as a promising tool for interconnecting embedded bionanomachines in the intra-body network (BAN).

We consider a scenario in which the transport protein channel fails due to disease; in this case, it is possible to implement a synthetic relay transport protein to perform the same function as the failed one. Consequently, we concentrate on developing a synthetic biological relay known as relay transport proteins (RTPs) that follows facilitated diffusion (FD) transport. Inspired by biological systems, the transport protein considers the cell's membrane to be a door that allows specific drug molecules to enter or exit the cell. As a result, based on FD, the synthetic RTP is capable of passing a high concentration of polar molecules from one side of the cell to the other. Consequently, the proposed RTPs can play important roles in calculating drug bioavailability, therapeutic efficacy, and pharmacokinetics.

The rest of this paper is organized as follows. Section 2 introduced the literature review and the main contribution of this work. Section 3 describes the design of the system model-based relay FRET nanocommunications as well as the FRET efficiency analysis. Section 4 presents the proposed RTP's channel capacity. Section 5 discusses the numerical results of. Finally the paper is concluded in Sect. 6.

2 Related Work

Recently, many researchers have been interested in molecular communications and its applications, particularly in medicine and targeted drug delivery (TDD) system [13, 14]. Bionanomachines (Bio-nanosensors or engineered bacteria, for example) could be implanted within the intra-body network (BAN) to monitor and diagnose diseases or to deliver therapeutic drugs to diseased cells. Furthermore, such bionanomachines may be linked to an external network, such as the Internet, using the Internet of bio-nano things (IoBNT) technology to control or guarantee precise medical treatment [15]. The communication between the bionanomachines is accomplished by the molecular communication technology. The molecular communication technology is used to communicate between the bionanomachines. The distance between bionanomachines is an important factor in achieving reliable molecular communication via diffusion. The relay concept was used by the researchers to improve the reliability of molecular communication. The authors of [16] proposed reliable communication between two populations of bacteria, whereas [17] proposed communication between two single bacteria. A single or population of biological agents, such as synthetic bacteria, is used to improve communication reliability, but these limits are considered major challenges due to obstacles such as food availability and waste disposal for them along the way, as mentioned in [16,17,18].

To improve communication reliability, the authors proposed a decode-and-forward relay scheme with depleted molecule shift keying based on signal processing theory [19]. The authors of [20] proposed a multi-hop amplify and forward relay scheme to evaluate the performance of bit error probability channel capacity via diffusion [21]. To mitigate inter-symbol interference (ISI) in dual transmission, the authors of [22] proposed a two-way relaying scheme with a transparent receiver based on XORing chemical reactions and a network coding scheme. Furthermore, the authors in [23] use a maximum a posteriori (MAP) detector to improve the reception process in terms of bit error probability in diffusion molecular communications based on relay [24].

On the other hand, the phenomenon of fluorescence resonance energy transfer (FRET) has been proposed for molecular communication. The importance of FRET lies in its ability to achieve high reliability molecular communication efficiency in a short period of time. FRET also has the advantage of being able to study protein–protein interactions in living cells, making it a popular technique for studying bi-molecular interactions. The synthetic bacteria, for example, can be replaced with ionised or polar molecules to convey information via the FRET principle [25]. This principle is composed of three major components: sensor polar molecules that act as transmitters, relay molecules, and actuator polar molecules that act as receivers. Using a large number of relays and a multistep FRET approach, the communication distance can be extended significantly [26]. This communication paradigm is analogous to multiple accesses and broadcast in traditional communication. In this paper, we consider a TDD scenario based on a molecular communication system with an embedded relay bionanomachine labeled with fluorescent molecules to deliver therapeutic drugs to the targeted tissues (cells). FRET-based on molecular communication outperforms other counterparts in MC paradigms [6]. Because FRET considers a discriminative solution to achieve high communication channel reliability, it has control over its intrinsic/extrinsic parameters and is influenced by environmental parameters. Following that, we consider molecular transmissions such as drugs, which are transmitted through the medium of the proposed molecular communication system using the FRET phenomenon. The idea of RTP is based on the conventional communication system-based relay concept and at the same time inspired by biological transport proteins such as protein channels (Pores). In this case, we consider a communication system composed of bionanomachines labelled with fluorescent molecules and referred to as the donor, relay, and acceptor, in that order. The FRET phenomenon is used to transmit drug molecules among bionanomachines. In the recent literature, the purpose of the relay was working to enhance and support the reliability of molecular communications; however, the proposed approach is relay transport protein (RTP) that synthesizes the plasma membrane in living cells, aims to convey polar molecules through Pores channel, and thus it is considered a bioengineered relay instead of failed protein's plasma membrane in the cell. The main contributions of this work are as follows:

• Proposing a synthetic RTPs based on embedded bionanomachines,

• Employing FRET phenomenon for nanocommunications among the embedded bionanomachines,

• Formulating the channel capacity of the proposed RTP,

• Comparing the performance evaluation of channel capacity with and without the proposed RTP, and

• Comparing the performance of the proposed approach with previous work.

3 System Model

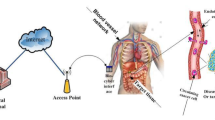
In this section, we present the design of the proposed system model as well as the analysis of information transmission in terms of energy transfer efficiency based on FRET. We consider the proposed MC system to be made up of transmitter bionanomachines (D_m), relay bionanomachines (R_m), and receiver bionanomachines (A_m) based on the FRET phenomenon as depicted in Fig. 1. The MC system is made up of interconnected polar molecules that contain the embedded drugs either externally (via light/laser) or internally (via bioluminescent molecules such as Luciferin), and these molecules are then transported through a synthesized RTP channel to reach biological membranes. All of these bionanomachines are labeled with fluorescent molecules (such as Alexa Fluor (AF)) to mimic enhanced green fluorescent protein (EGFP), enhanced yellow fluorescent protein (EYFP), or enhanced cyan fluorescent protein (ECFP), allowing them to perform FRET nanocommunication.

Fig. 1

Concept of relay-based FRET nanocommuniation

3.1 Relay-Based FRET

The achievement of fluorescent molecules as a probing tool for inspection dynamics of biochemical and biological systems comes from the high sensitivity of fluoro-metric techniques as well as the specificity of fluorescence characteristics due to the microenvironment of the emitting molecule and temporal information. As a result, FRET is an electrodynamic nanocommunication approach in which nonradiative energy transfer can occur among polar molecules labeled with fluorophores such as agent proteins, organic dyes, quantum yields, and polymers [27]. Fluorophores are fluorescence molecules that are excited optically at a specific wavelength. We assume that when polar donor molecules labeled with a fluorophore are excited, they sequentially transfer energy to other polar molecules. Because the interaction of dipole molecules has a significant impact on the efficiency of energy transfer, the following conditions must be met in order to satisfy efficient energy transfer-based FRET.

• A pair of polar molecules must be located proximally at a distance ranging from 0 to 10 nm apart,

• Maximum overlap at 50% of wavelength and spectral similarity between emission molecule D_m (i.e., sensor or donor) and absorption molecule A_m (i.e., acceptor) must be realized, and

• Orthogonal orientation leads to failure of the FRET concept.

The above conditions in the proposed system model result in the FRET principle, which can be extended to a wide range in the 3D aqueous medium environment. The communication relay molecules R_m can transfer energy from the excited state of the D_m molecule to the ground state of the A_m molecule. We consider that the exciton is the required drug molecule that we want to deliver to the target tissue [28]. Therefore, identical excitons or drugs are performed by homo FRET technology as shown in Fig. 1. Finally, excitons as a form of energy transfer reach A_m after a journey from D_m to sequential R_m relays. We assume the spectral overlapping occurs in the forwarding direction and overlap of the reverse direction is neglected.

3.2 FRET Propagation-Based Facilitated Diffusion

The proposed synthetic RTP approach is inspired by multi hop based-FRET that includes donor, acceptor and relay polar molecules as demonstrates in Fig. 2. This approach is inspired by living cell and circulation system and thus the successful treatment is achieved when drugs move to blood vessels. In the proposed approach, once patient takes drugs by mouth, these molecules diffuse from small intestine to blood vessels, inhaled orally by smell to arrive air sac of lungs or directly injected in blood vessel and diffuse passively by FD in blood stream based concentration gradient [25, 29]. Figure 2 depicts the movement of polar molecules into and out of a cellular membrane, specifically a selective bipolar membrane (SBM). The thickness of the bilayer phospholipids in SBM regulates the movement of molecules inside and outside the cell. Each phospholipid has a polar head and a unipolar tail that allows uncharged small molecules to pass through. FD is used to diffuse molecules from high to low concentrations in a concentration gradient. Because of its repulsion with the SBM membrane (i.e., phospholipids), it necessitates the presence of a channel and a carrier protein, which are in charge of transporting polar molecules. Moving only based on concentration gradients, such as glucose molecules, requires no energy. While osmosis is the passive diffusion of water from high to low concentrations through the cell SBM, i.e., the phospholipid membrane, or through a direct channel called the aquaporin channel, no energy is required.

Fig. 2

Proposed synthetic RTP channel-based facilitated diffusion (FD)

From point of view of molecular communication system, we consider the polar molecules that carry the required drugs are followed the Brownian motion and thus propagated according to the facilitated diffusion (FD) property. Upon concentration gradient, FD of polar molecules spreads with Brownian motion in cellular tissues. Polar molecules can't pass the SBM owing to exist of repulsion force with it. Upon that, it arises from localized protein across the membrane, we called this protein as RTP because it works as a channel for the embedded therapy or information until they arrive to blood vessels.

In the literature, the purpose of the relay is to enhance and support information molecules, but in this case, RTP is used to convey polar molecules through its channel (i.e., channel mediate). We can simulate the movement of polar molecules using Fick's law. The following equation gives ${Q}_{p}$ as the difference in concentration between two regions ${c}_{1}$ and ${c}_{2}$ at the cell's membrane surface

$$\frac{\Delta c}{\Delta s}= \frac{{c}_{1}-{c}_{2}}{\Delta s}$$

(1)

where ∆$c$ is the concentration gradient and ∆$s$ is the totals distance of FD molecules.

$${Q}_{p}= -({ k}_{diff} A)\frac{dc}{ds}$$

(2)

where ${k}_{diff}$ is diffusion coefficient of the medium, $A$ the normal area, and $\frac{dc}{ds}$ is the concentration gradient. Polar molecules ${Q}_{p}$ interrelated under the influence of FRET, therefore, using Forester principle, we can express Forester radius R₀ as follow [13];

$${R}_{0}= \sqrt[6]{\frac{9000\mathrm{ln}\left(10\right){k}^{2}{Q}_{D}J\left(\lambda \right)}{128{\pi }^{5}N{n}^{4}}}$$

(3)

where orientation factor refers to ${k}^{2}$, where its value ranges between 0 and 4. Usually, most of the experimental studies assumed ${k}^{2}$ to be mean value (i.e., 2/3) [27]. ${Q}_{D}$ is the quantum yield of polar donor molecules D_m, $n$ is the refractive index of the 3-D blood plasma. $N$ is Avogadro number and J(λ) is an integral function employs for identifying the degree of overlap between emission and absorption spectra of polar molecules.

The separated distance, R is the intermolecular distance of polar molecules, which has a significant impact on the efficiency of energy transfer-based FRET. We can model FD in terms of separation distance R using the stochastic process as follows. [6]:

$$\frac{dR}{dt}=\left(-\frac{1}{\gamma }\right) {\varPhi }^{\mathrm{^{\prime}}}\left(R\right)dt+\sqrt[2]{2 {D}_{s}} \frac{d{B}_{t}}{dt}$$

(4)

where $\gamma$ refers to the effective drag, $\varPhi$ is the free energy potential of the separated distance $R$, ${D}_{s}$ the effective diffusivity, and ${B}_{t}$ Brownian motion. This equation is interpreted in termed of Ito calculus [30]. The separation distance of FRET- pair D_m– A_m can be modeled over the potential of free energy equations as follow:

$$\varPhi \left(r\right)=\frac{K}{2} {\left(r-R\right)}^{2}$$

(5)

In order to parameterize the model, we utilize diffusivity of the effective drag $\gamma = {K}_{B}( \frac{T}{{D}_{s}}$) where at separated distance R approaches zero, modeled can be happened.

3.3 Efficiency of RTP-Based FRET

The efficiency of RTP is a function of energy transfer between polar molecules D_m and A_m and thus a function on separation distance, it can be formulated as:

$$\mu \left(R\right)=\frac{{R}_{0}^{6}}{( {R}_{0}^{6}+{R}^{6})}$$

(6)

where ${R}_{0}$ is Forester radius that can be illustrated in (2), and $R$ is separation distance between pair of polar molecule. Actually, the total duration time of drug transfer can be expressed as [27],

$${T}_{t }\left(R\right)= {\tau }_{Dm}{\left(R|{R}_{0}\right)}^{6}$$

(7)

where ${\tau }_{Dm}$ is the mean occupied time of donor molecule in its excited state that is reciprocal of emission rate ${k}_{R}$. In order to derive the complete duration time of FRET communication technology between pair of ionized molecule, it must be reduction as follow

$${\tau }_{DmAm}= {\tau }_{Dm}+ {T}_{t}$$

(8)

We assume drugs are single excitons that exchange between polar molecules and are interested in the efficiency and optimum capacity that can be obtained by varying ${R}_{0},$ $R$, $n$, ${k}^{2}$ in a single step and wireless excitation probability, ${p}_{e}$ of laser source (LS) and $R$ at simple multi-step of FRET. FRET probability (i. e., efficiency) is proportion between number of FRET relaxation time occurs and net of relaxation process at the same time. Thereby, the transmission efficiency, is a function in intermolecular distance, is given by

$${\upmu }_{FRET}\left(R\right)={p}_{thera}=\frac{{R}_{0}^{6}}{{R}_{0}^{6}+ {R}^{6}}$$

(9)

We investigate the most basic form of wide range communication-based FRET, in which the donor molecule D_m is located at the transmitter bionanomachine and the acceptor molecule A_m is located at the receiver bionanomachine. R_m, the relay molecule, is in the center. R_m assumed to be arranged linearly and applied two step FRET technologies thus separation distance is the total distance from D_m to R_m molecule and from R_m to A_m which can be given by

$${R}_{{D}_{m}{A}_{m}}= {R}_{{D}_{m}{R}_{m}}+ {R}_{{R}_{m}{A}_{m}}$$

(10)

The overall overlapping is particularly high, with overlapping between D_m and R_m molecules equaling overlapping between R_m and A_m molecules. As a result, there are two independent cascaded communication channels whose efficiency, µ can be calculated using the following equation,

$${\upmu }_{{D}_{m}{A}_{m}}= {\upmu }_{{D}_{m}{R}_{m}}+ {\upmu }_{{R}_{m}{A}_{m}}$$

(11)

The FRET efficiency of a single exciton from donor D_m until it is delivered to the targeted acceptor A_m polar molecule via relay can be expressed as follows:

$${\upmu }_{FRET,DA}\left({R}_{{D}_{m}{R}_{m}}, {R}_{{R}_{m}{A}_{m}}\right)=\left(\frac{{R}_{0,{D}_{m}{R}_{m}}^{6}}{{R}_{0,{D}_{m}{R}_{m}+ }^{6}{R}_{{D}_{m}{R}_{m}}^{6}}\right) \times \left(\frac{{R}_{0,{R}_{m}{A}_{m}}^{6}}{{R}_{0,{R}_{m}{A}_{m}}^{6}+ {R}_{{R}_{m}{A}_{m}}^{6}} \right)$$

(12)

In order to obtain a closed form expression for channel capacity of the proposed RTP channel, we consider the probability (p_thera) of successfully delivering therapeutic drug to the target cell as equal to the FRET efficiency ${(\mu }_{FRET,DA})$ in Eq. (12).

4 Channel Capacity of RTP

Channel capacity is generally defined as the maximum rate of data transmission, i.e., mutual information between transmitter and receiver. RTP functions as both a relay and a channel protein, and it is in charge of the interpretation and transport of ionised information molecules and thus it is a safe communication channel. As previously stated, the drug molecules (information) are freely diffused using FD and FRET nanocommunications technology [25]. Furthermore, channel capacity is critical for optimizing both bandwidth and power, with maximum or optimum capacity influenced significantly by intrinsic and environmental parameters such as medium refractive index, orientation factor, intermolecular distance, and radius. As a result, a closed-form expression of RTP channel capacity must be derived.

Using the block diagram in Fig. 3, the proposed RTP channel capacity can be described as follows [31]:

• Channel can be modeled as four finite sets, X_a, X_b, Y_a, and Y_b and a conditional probability distribution, p(Y_b, Y_a|X_a, X_b);

• Embedded drugs by using external source (i.e. light/laser) or internally by employing bioluminescent molecules (such as, Luciferin), within cellular membrane mimics through wireless channel probability as $p\left({X}_{b}|{X}_{a}\right)$,

• Biological RTP on aqueous medium has been implemented on SBM in order to transport therapeutic molecules into the circulation system with channel probability $p({Y}_{b}|{Y}_{a})$ at the same medium.

• Particularly, ${Y}_{a}$ does not effect on ${X}_{b}$, thus, it can be reasonable that ${X}_{a}$ to be neglected. Therefore, $p({Y}_{b}|{Y}_{a})$ is essential to refine and thus filtering of power and B.W channel.

• Applying the relay channel with joint probability, $p\left({X}_{b}, {Y}_{b}\left|{X}_{a}\right)=p\left({X}_{b }|{X}_{a}\right). p({Y}_{b}|{X}_{b}\right)$. Subsequently, the total biological RTP channel capacity, $C$ with respect to mutual information I(X, Y) can be expressed as

  $$C=\underset{p({X}_{a , }{Y}_{a })}{\mathrm{sup}}\mathrm{min}\{I\left({X}_{\alpha },{Y}_{\alpha };{Y}_{\alpha }\right),I\left({X}_{\alpha };{X}_{b}|{Y}_{b}\right)\}$$

  (13)

where ${X}_{a}$ is the therapy that must stimuli sensor (donor) polar molecules D_m to be excited. Moreover, the stimulation is transferred in 3-D environment within SBM while arriving targeted molecules called therapeutic molecules. As a result of FRET nanotechnology, these molecules are linked together, and RTP transports therapeutic molecules into blood vessels. Therapeutic molecules include glucose molecules in the intestines, oxygen molecules in the air sacs, and exchanged molecules of the sodium–potassium pump in ATP or ion channels in the neuron system. Each case has a unique therapeutic molecule with a joint probability, p_thera, represented by FRET efficiency, as shown in Eq. (12).

Fig. 3

Capacity of RTP channel-based relay

In order to obtain the mutual information equation, we consider the RTP channel to be a symmetric binary channel according to the Z-channel, as inspired by wireless communication systems:

$$I({X}_{a}, {Y}_{b})=H\left[ {p}_{e }. {p}_{thera}\right]- {p}_{e} H \left[1- {p}_{thera}\right]$$

(14)

where p_e denotes the excitation probability of donor bionanomachine that is defined as a priori probability for transmission 0 or 1. The entropy function denoted by H[.]. According to ON–OFF keying modulation, sending bit 1 at the beginning of transmission a single exciton message, accordingly received bit may be 1 or 0. As a result, bit 1 indicates that therapy was successfully delivered, while bit 0 indicates that therapy was not delivered. Using the characteristics of the Z-channel model [32], the capacity of the proposed approach, RTP channel is the maximization of mutual information, $I\left({X}_{a},{Y}_{b}\right)$, as follows:

$${C}_{max}=\mathrm{max}\left\{I\left({X}_{a},{Y}_{b}\right)\right\}=\mathrm{max}\{H\left[ {p}_{e} . {p}_{thera} \right]- {p}_{e} H \left[ 1- {p}_{thera} \right] \}$$

(15)

Therapeutic molecules are transported using the FD method through the RTP channel, which is linked using the multi-hop FRET method. To evaluate the channel characteristics of the proposed approach, we are limited to studying, evaluating, and analyzing the channel capacity of three interconnected molecules, which are donor, relay, and acceptor bionanomachines labeled by fluorescent molecules, as shown in Fig. 1.

5 Numerical Results

In this section, we present the numerical results to evaluate the performance of the proposed approach. We consider a scenario of smart drug delivery system [3, 7, 14] for transmission therapeutic drugs that carried by polar molecules through RTP channel. The propagation of polar molecules are passively diffused by DF. Subsequently, we employed the proposed MC system-based FRET that mimics the RTP channel between the blood vessel and plasma membrane at the cell. We assumed that the MC system consists of three nanodevices namely: donor, relay and acceptor bionanomachine, labeled by fluorescent molecule. The interconnection is accomplished through FRET nanocommunications, and thus information (therapeutic drugs) is exchanged by the exciton among the proposed bionanomachines.

We designed the proposed approach to work in a short distance (the distance between the blood vessel and the cell's plasma membrane), which was changed from 3 to 6 nm, according to the FRET principle. At human temperature, the refractive index, n, of blood plasma is 1.351. We considered rapid randomization of fluorescent molecules and thus the orientation factor, ${k}^{2}$=2/3 [33]. In addition, we used different fluorescent protein pairs to study the performance of the synthetic RTP channel, such as ECFP–EYFP and ECFP–EYFP–EGFP.

The purpose of this section is to discuss the effects of intrinsic and environmental factors on the capacity performance of RTP channels, as well as separation distance. Furthermore, we intend to demonstrate the performance difference with and without the proposed synesthetic RTP channel. However, for the sake of simplicity, we consider the linear multi-hop between each FRET pair, whereas the proposed approach can be applied to a variety of multi-hop scenarios. As a result, we first demonstrate the numerical analysis of key parameters that influence the design of the synesthetic RTP channel. The performance of the proposed MC system with and without the proposed RTP channel is then presented.

5.1 Optimum Efficiency of RTP Channel

In this section, we present a performance evaluation of the RTP channel's efficiency as a function of separation (intermolecular) distance between the relay bionanomachine and both the donor and acceptor bionanomachines. The goal of this evaluation is to find the optimal amount of RTP channel capacity as the separation distance varies. We begin by demonstrating the effect of separation distance between the relay bionanomachine and both donor and acceptor bionanomachines on the probability of drug delivery using FRET technology, as derived from Eq. (12). To achieve the multi-hop property, we modify a simple linear arrangement of the three nanomachines. We consider the FRET technology configuration pair of ECFP-EYFP-EGFP as performed experimentally in [34] and then ECFP, EYFP, and EGFP mimic the donor, relay, and acceptor bionanomachines respectively.

The following are the parameters of the proposed MC-system based on the FRET phenomenon. The orientation factor, ${k}^{2}$=4 and refractive index of blood plasma at human temperature, n = 1.531. We assumed a molecular communications-based relay scenario, with only one relay bionanomachine, R_m in the intermediate distance between the donor D_m and the acceptor A_m. The overall distance between the D_m and the A_m i.e., ${R}_{{D}_{m}Am}$ as illustrated in Eq. (10). We are setting the default values of Forster radius, ${R}_{0,ECFP-EYFP}$, ${R}_{0,EYFP-EGFP}\mathrm{ as }4.92$ and $3.25$ respectively [34].

We employed the contour plot to draw the 3D dimension among${R}_{{R}_{m}{A}_{m}}$, ${R}_{{D}_{m}{R}_{m}}$ and $\mu$ in two dimension as shown in Fig. 4. The idea behind using contour plot is to predict the proper separation distance ${R}_{{R}_{m}{A}_{m}}$ and ${R}_{{D}_{m}{R}_{m}}$ to achieve the optimum FRET efficiency ($\mu$). As we can see in Fig. 4, the successful probability of drug delivery (i.e., the FRET efficiency) increases under the condition of ${R}_{{D}_{m}{R}_{m}} > {R}_{{R}_{m}{A}_{m}}$ is accomplished. For example, we can see the FRET efficiency is equal to$\mu =90\mathrm{\%}$, can be achieved when ${R}_{{D}_{m}{R}_{m}}$ changed from 2 to less than 2.5 nm while ${R}_{{R}_{m}{A}_{m}}$ changed from 2.5 to less than 3 nm. On the other hand, the FRET efficiency significantly decreased by increasing the separation distance ${R}_{{R}_{m}{A}_{m}}$ or${R}_{{D}_{m}{R}_{m}}$. For example, FRET efficiency $\mu =10\mathrm{\%}$ is achieved when ${R}_{{D}_{m}{R}_{m}}$ changed from 2 to 6 nm while ${R}_{{R}_{m}{A}_{m}}$ changed from 2 to 4.75 nm. Therefore, an interesting observation was that the presence of an intermediate relay near to donor bionanomachine is able to sensitize the FRET efficiency and thus can extend the detectable distance range to reach to the targeted acceptor bionanomachines, in the case of the Forster distance ${R}_{0,ECFP-EYFP}$>${R}_{0,EYFP-EGFP} .$

Fig. 4

Contour plot to represent 3D relationship among μ, ${R}_{{R}_{m}{A}_{m}}$ and ${R}_{{D}_{m}{R}_{m}}$

5.2 Optimum Capacity of RTP Channel

Following that, in order to achieve the reliability of the molecular communication channel, according to Eqs. (10) and (15), the performance of RTP channel capacity depends on R and excitation probability, p_e. We defined p_e, as the a priori probability of transmitting one bit (i.e. the therapeutic drug). We want to find the best excitation probabilities for achieving the best RTP channel capacity. We also employ contour plot to draw the 3D dimension among ${R}_{{R}_{m}Am}$, ${R}_{{D}_{m}Rm}$ and ${C}_{max}$ in two dimension as depicted in Fig. 5. We test different values of the excitation probability such as, p_e = 0.2, 0.5 and 0.8 as illustrated in Fig. 5a–c. As we can observe, the influence of separation distance between relay bionanomachine and both donor and acceptor bionanomachines in terms of ${R}_{{D}_{m}{R}_{m}}$ and ${R}_{{R}_{m}{A}_{m}}$. The figures show that when p_e is small, the optimum value of C_max occurs at a short separation distance between R_m and both D_m and A_m bionanomachines. This is because when small values of p_e are used, mutual information increases and thus channel capacity is maximized, resulting in therapeutic drug transmission that is reliable and thus RTP channel that is not error prone significantly. On the contrary, even though the separation distance between R_m and both D_m and A_m bionanomachines is short, achieving C_max is impossible when p_e is large, as shown in Fig. 5c.

Fig. 5

Contour plot to represent 3D relationship among C_max, ${R}_{{R}_{m}Am}$ and ${R}_{{D}_{m}Rm}$ a RPT channel capacity at ${p}_{e}$ = 0.2 with varying C_max. b RTP channel capacity at ${p}_{e}=$ 0.5 with varying C_max. c RTP channel capacity at ${p}_{e}=$ 0.8 with varying C_max

5.3 Performance Comparison

The goal of this section is to demonstrate the efficacy of the proposed RTP channel approach. As a result, we compare the performance of the molecular communication (MC) system with and without the proposed approach. As previously discussed, the effectiveness of adjusting the separation distance between the relay and both the donor and acceptor bionanomachines is required for improving the performance of the proposed RTP channel. In the absence of the proposed approach, we fixed the separation distance between donor and acceptor bionanomachines at 3 nm in the case of MC systems. However, when the MC system used the proposed RTP channel, we investigated different separation distances between the relay and both the donor and acceptor bionanomachines, but we still kept the separation distance between the donor and acceptor bionanomachine at 3 nm, as shown in Fig. 6a–c. We look at the following scenarios:

• (a) If ${R}_{DRm}$=2 nm and ${R}_{RAm}=1$ nm, that is meaning that the relay is close to the acceptor bionanomachine as depicted in Fig. 6a,

• (b) If ${R}_{DRm}$= 1 nm and ${R}_{RAm}$ = 2 nm, that is meaning that the relay is almost far away from the acceptor bionanomachine as depicted in Fig. 6b,

• (c) If ${R}_{DRm}$ =0.5 nm and ${R}_{RAm}$ =2.5 nm, that is meaning the relay is very far away from the acceptor bionanomachine as depicted in Fig. 6c.

Fig. 6

Performance comparison of capacity for MC system with and without proposed RTP channel. a C_max.versus p_e at ${R}_{DRm}$=2 nm and ${R}_{RAm}=1$ nm. b C_max.versus p_e at ${R}_{DRm}$=1 nm and ${R}_{RAm}=2$ nm. c C_max.versus p_e at ${R}_{DRm}$=0.5 nm and ${R}_{RAm}=2.5$ nm. d Performance comparison with related work [26]

Furthermore, we compare the proposed approach to previous work [26] to examine the accuracy of the proposed approach. We set the distance between donor and acceptor bionanomachines to 3 nm and used the same system parameters. In the previous work, the relay bionanomachine is located in the center, whereas in our proposed approach, the relay bionanomachine is close to the transmitter bionanomachine, as recommended by the preceding discussion. Figure 6d plots the maximum channel capacity against the excitation probability, p_e, for both the proposed approach and the previous work [26]. As we can see, the proposed approach has a higher channel capacity than previous work. This is because the proposed approach takes into account the physical structure of the diseased cell by stimulating a relay transport protein (RTP) channel between the blood vessel and plasma membrane at the diseased cell, resulting in the drug information being transferred directly to the cell. Furthermore, when the RTP is close to the transmitter, the performance for drug transmission improves. When compared to previous work, the proposed approach increases the channel capacity gain by approximately 16.7%.

We can conclude from the figures that when the relay bionanomachine is close to the donor bionanomachine (i.e., nanotransmitter), the performance of the channel capacity for the MC system with the proposed RTP approach is superior to the performance of the MC system without the proposed approach. It is significant that the synesthetic relay protein transport will be placed near a blood vessel that contains donor bionanomachines, allowing the therapeutic drug to efficiently transport through the RTP channel to the acceptor bionanomachines. Consequently, during the design of the molecular communication-based relay concept, we recommend placing the relay bionanomachines close to the donor bionanomachine (i.e. the transmitter).

6 Conclusion

The approach proposed in this paper is an embedded synthetic biological relay transport protein (RTP). If the channel protein fails, the proposed approach is a bioengineered protein that works on the plasma membrane of the targeted cell to allow communication between the blood vessel and the cell's tissues. The proposed approach is based on FRET nanocommunications to ensure high communication efficiency. The performance of the proposed RTP is described in terms of RTP channel capacity as a function of separation distance between the embedded and proposed relay bionanomachines. The numerical results show that using the proposed approach improves the performance of the molecular communication (MC) system significantly.