1 Introduction

Wireless sensor networks (WSNs) consist of a set of sensor nodes which together sense an event signal generated by a source in an event area [1, 2]. The readings of these sensor nodes are then forwarded to the Base Station (BS) to be accessible at the end user. The deployment of the sensor nodes can be either random or fixed based on the application requirements [3]. The random deployment allows a WSN to be scattered over unreachable environments such as battlefield. However, when deployment is random, it is not guaranteed that the sensor nodes cover all the event region [4]. This coverage challenge can be handled by increasing density of nodes. In this case, sensor readings may be spatially-correlated, which makes some sensor nodes reporting redundant and nonessential readings[5, 6].

The main aim of this paper is to determine and eliminate these sensor nodes which are inessential to reconstruct the source event signal while keeping an acceptable distortion. To this end, the event distortion-based clustering (EDC) algorithm is proposed for a WSN in which sensor nodes are assumed to harvest their energy from ambient electromagnetic radiation source [7]. The EDC algorithm involves two main operations. The first one is the node elimination, based on the reliability threshold. In this step, the nonessential sensor nodes are determined and eliminated. The second operation is the clustering formation. In this operation, the sensor nodes are clustered by using vector quantization (VQ) scheme, and sensor node locations are an input. The operations of the EDC algorithm are given for both single-hop and two-hop communication models. For each of those models, a different distortion function is derived and employed within the EDC algorithm, to verify the reliability performance level. The performance of the EDC algorithm is evaluated by using different metrics such as achieved distortion level, number of alive nodes and harvestable energy levels. As a result, the EDC algorithm can successfully exploit both spatial correlation and energy harvesting, while preserving an acceptable level of distortion, to improve the energy efficiency. Furthermore, the performance comparisons reveal that the two-hop communication model outperforms the single-hop model in terms of distortion level and energy-efficiency.

The remaining parts of this paper are organized as follows. In Sect. 2, the related works are introduced. The system models and assumptions are given in Sect. 3. By introducing the distortion functions for the single-hop and two-hop communication models, the operations of the EDC algorithm are presented in Sect. 4. The EDC performance evaluations and simulation results are discussed in Sect. 5. Then, the concluding remarks and future directions are given in Sect. 6.

2 Related Works

One of the most eminent algorithms to utilize spatial correlation in WSNs is given in [6]. In particular, the Iterative Node Selection (INS) algorithm is proposed in [6] to eliminate the nonessential nodes by jointly employing both Vector Quantization (VQ) and reconstruction distortion for event signal. The INS algorithm determines a set of representative nodes to represent all the nodes to ignore and eliminate the remaining ones. The INS algorithm is based on just a single-hop channel communication model, and it does not consider the channel noise in the derivation of the reconstruction distortion function for VQ. Furthermore, the INS algorithm considers only the sensor nodes that battery-powered based, and the energy-harvesting based sensors are not considered.

In [8], which is the conference version of this paper, we presented an event distortion-based node selection (EDNS) algorithm for a WSN with energy-harvesting sensor nodes. The EDNS algorithm is based on a single-hop communication channel model. The two-hop communication model and the associated reconstruction distortion function are not taken into consideration by the EDNS algorithm. Hence, both INS and EDNS algorithms are based on only single-hop communication model whose energy consumption rate is higher than the two-hop communication model as will be clarified later.

Many clustering algorithms have been also introduced in the WSN literature [9], to improve energy-efficiency by exploiting correlation among sensor nodes. In [10], the correlated clusters are formed, and the associated cluster heads are determined based on both the degree of correlation and residual energy. Furthermore, the size of each cluster is determined by using the correlation threshold. In each cluster, one sensor node is responsible for reporting the sensed readings to the BS, and the remaining nodes are kept in sleep state. Although the proposed algorithm can significantly reduce the energy consumption rate, but it does not take into account the reliability of the data delivered to the BS through a distortion function or any other error control scheme.

In [11], energy balanced distributed clustering protocol (EBDCP) is proposed. The main aim of this work is to balance the distribution of energy consumption over the entire sensor network. The selection of cluster heads and the formation of clusters are achieved so that the total energy consumption of the sensor network is reduced. However, EBDCP does not consider the reliability of sensor network in clustering formation and cluster head selection. In [12], the authors propose energy harvesting–cluster head rotation scheme (EH-CHRS) algorithm to minimize the energy overflow and energy outage. This is done by optimally selecting cluster head (CH) and CH rotation scheme based on energy harvesting rate and the distance to the sink node. Also, in this paper, the author does not consider the reliability level of the sensor readings in selection and rotation of CHs. In our work, we consider energy level at each sensor with respect to energy harvesting rate, distance to the sink node, and reliability of sensor readings to select the optimal CHs and organize clusters while minimizing the distortion function.

In [13], based on the single-hop communication model, the number of sensor nodes reporting the event data are reduced by clustering the sensor nodes. This reduction is done by using two approaches: greedy corrected clustering (GCC) and K-means clustering algorithms. The GCC algorithm has the similar principles to [10]. However, in [13], the representative nodes are elected based on the reconstruction distortion function for the event signal. The distortion function has the similar form that used in [6] and [8]. In [14], K-means clustering algorithm has been implemented with respect to temporal correlation of sensed data to reduce the cost of transmissions and eliminates the redundant data. The accuracy of the communication is investigated based on data loss ratio. However, the locations of sensor nodes and the way how sensed data are relayed to the sink node are not taken into account to investigate the accuracy. Next, the network model and assumptions are introduced.

3 System Model

3.1 Network Model

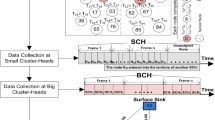
The network is considered as a set of M sensor nodes which are denoted by \(n_i, i \in \{1,2,\ldots ,M\}\), where each of these sensors is homogeneous node. Furthermore, these sensor nodes are scattered for observing a physical phenomenon, which generates an event signal, i.e., S, in the event area. Each sensor node is capable to harvest energy and send its data to the sink node. The data can be sent through single-hop (point-to-point) and multi-hop communication models as shown in Fig. 1. The sink node or Base Station (BS) is assumed to be located at the center of the network. In addition, the following assumptions are considered for the rest of the paper:

  • Sensor nodes are dense and randomly scattered in the event area.

  • Each sensor node is capable of regulating its transmission power levels.

  • Sensor nodes are equipped with RF harvesting unit to harvest energy from ambient electromagnetic radiation source.

Fig. 1
figure 1

Illustration of a wireless sensor network

Full size image

3.2 Energy Consumption Model

In this section, the energy model of the sensor nodes is explained. The first order radio model [15] is used to model the energy consumption of sensor nodes. The energy consumption for transmitting L number of bits over d meters, i.e., \(E_{TX}(L,d)\), and to receive L number of bits, i.e., \(E_{RX}(L)\), are given as

$$\begin{aligned} E_{TX}(L,d)= & {} \left\{ \begin{array}{cl} (\epsilon _{elec} L) + (\epsilon _{fs} L d^2) &{} d \le d_0\\ (\epsilon _{elec} L) + (\epsilon _{mp} L d^4) &{} d > d_0 \end{array}\right. \end{aligned}$$
(1)
$$\begin{aligned} E_{RX}(L)= & {} \epsilon _{elec} L \end{aligned}$$
(2)

where \(d_0\) is the threshold distance in meter, and it can be calculated by \(d_0=\sqrt{\epsilon _{fs}/\epsilon _{mp}}\), and \(\epsilon _{elec}\) is the electron energy. Both \(\epsilon _{fs}\) and \(\epsilon _{mp}\) are consumed energy for amplifier in free space and in multi-path models, respectively. Furthermore, the consumed energy for sensing L bits is defined as follows

$$\begin{aligned} E_{sens}(L)=L T_{sens} I_{sens} V_{sub}, \end{aligned}$$
(3)

where \(I_{sens}\) and \(V_{sub}\), are respectively the sensing current and supplied voltage over the sensing time \(T_{sens}\). Furthermore, the consumed energy for aggregating the readings from m sensor nodes, i.e., \(E_{agg}\), is given as

$$\begin{aligned} E_{agg}(L,m)= L m E_{DA}, \end{aligned}$$
(4)

where \(E_{DA}\) is consumed energy per bit for data aggregation. For single-hop communication channel model, then the total consumed energy for sensor node i to sense and transmit L number of bits to the BS, i.e., E(i), is given as

$$\begin{aligned} E(i)=E_{sens}(L)+E_{TX}\big (L,d(i)\big ) \end{aligned}$$
(5)

where d(i) represents the distance in meter between the sensor node i and the BS. On the other hand, for two-hop communication model, the network is clustered. Hence, the consumed energy depends on the sensor node role. If the senor node is cluster member (CM), then the consumed energy of the CM i at the cluster k is given as

$$\begin{aligned} E_{CM}(k,i)=E_{sens}(L)+E_{TX}\big (L,d(k,i)\big ), \end{aligned}$$
(6)

where d(k, i) is the distance in meter between the CM i and cluster head (CH) k. And if the sensor node is CH, then energy consumption for CH k is given by

$$\begin{aligned} E_{CH}(k)=E_{agg}(L,m_k)+m_k E_{RX}(L)+E_{TX}(L,d(k)) \end{aligned}$$
(7)

where d(k) are distance between CH k and the BS, and \(m_k\) is the number of CMs in the cluster k.

3.3 Energy Harvesting Model

In this paper, a radio frequency (RF) electromagnetic source is assumed to be located in the event region. As in [16] and [17], the source is modelled as GSM900 cell tower. In addition to an antenna used for the data communication, each sensor node is assumed to have an RF harvesting circuit with a dedicated antenna whose receive gain is given by \(G_R\). Hence, by using the Friis equation, the received power, i.e., \(P_R\), can be written as

$$\begin{aligned} P_R=P_T \frac{G_T G_R \lambda ^2}{(4 \pi d)^2} \end{aligned}$$
(8)

where \(P_T\) and \(G_T\), respectively, are transmitted, power and antenna gain. And \(\lambda\) is wavelength for the receiving signal and d is the distance between the RF cell tower source and the sensor node.

4 Event Distortion Based Clustering (EDC) Algorithm

In this section, the EDC algorithm is discussed. The EDC algorithm executes at the BS to generates the clusters of the sensor nodes so as to determine which sensor nodes should report their readings to the BS for an acceptable level of event signal reconstruction distortion. The operations of the EDC algorithm are driven by two distortion functions, which are derived next for the single-hop and two-hop communication models. These distortion functions are used to introduce the operations of the EDC algorithm at the later sections.

4.1 Distortion Function for Single-Hop Communication Model

The used model for the single-hop communication with M number of sensors is illustrated in Fig. 2, as in [6]. Here, the aim of BS is estimating the source event signal, S, based on the noisy sensor samples. Let \(X_i[k]\) denote the \(k^{th}\) sample of the event information \(S_i\) taken by node i. By dropping the time index k, the \(X_i[k]\) is then can be given as follows

$$\begin{aligned} X_i =S_i +N_i, \end{aligned}$$
(9)

where \(N_i\) denotes the samples for the observation noise process of independent and identically distributed (i.i.d.) Gaussian random variable with zero mean and variance \(\sigma _N^2\). And \(S_i\) represents the samples of the physical source event signal, which are sensed at the location of the sensor node i. These samples are also modelled as a set of Gaussian random variables with zero mean and variance \(\sigma _S^2\). To model the correlation between sensor nodes, the power exponential model [6] is used. It is defined as the correlation coefficient, \(\rho (S_i,S_j)\), between the signal samples \(S_i\) and \(S_j\), which are sensed by the nodes i and j, respectively, as introduced as

Fig. 2
figure 2

Point-to-point network model

Full size image
$$\begin{aligned} \rho (S_i,S_j)=\frac{E[S_iS_j]}{\sigma _S^2}=e^{(d(i,j)/\theta _1)^{\theta _2}}, \end{aligned}$$
(10)

where d(i, j) is the Euclidean distance in meter between node i and node j. And \(\theta _2\) is set to be 1. Also, \(\theta _1\) is used for adjusting the relation between correlation coefficients, \(\rho (S_i,S_j)\), and inter-node distance, d(i, j). Hence, \(\theta _1\) is defined based on the sensing range of each sensor node, which can be estimated based on all sensors’ readings [6]. However, such an estimation is beyond the scope of this paper. For simplicity, in the performance evaluations of this paper, \(\theta _1\) is set to be 1000.

In order to report the noisy observation, \(X_i\), given in (9), to the BS, the node i should forward its readings over the single-hop noisy channel, \(W_i\). Then, the received signal, i.e., \(Y_i\), at the BS, can be defined as

$$\begin{aligned} Y_i=\alpha _i X_i + W_i, \end{aligned}$$
(11)

where \(W_i\) is a set of i.i.d Gaussian random variables with zero mean and variance \(\sigma _W^2\). Each sensor node transmits a scaled version of the observed sample, \(X_i\), to meet its power constraint. More clearly, the scalar, \(\alpha _i\) in (11), can be defined as

$$\begin{aligned} E[\big (\alpha _i X_i\big )^2] \le P_i, \end{aligned}$$
(12)

where \(P_i\) is the power constraint. Both \(S_i\) and \(N_i\) are assumed to be uncorrelated, hence the power of \(X_i\), in (9), is restricted by \(\sigma _S^2+\sigma _N^2\). Hence, in order to meet the power constraint, \(\alpha _i\) is defined as

$$\begin{aligned} \alpha _i=\sqrt{\frac{P_i}{\sigma _S^2+\sigma _N^2}}. \end{aligned}$$
(13)

The BS is started to calculate the estimation of each event information, \(S_i,\;i \in \{1,2,\ldots ,M\}\), after receiving all the readings of the sensor nodes, \(Y_i,\;i \in \{1,2,\ldots ,M\}\). The decoding operation is applied for each of \(Y_i\) readings using the decoder block D.

As in [8], the uncoded transmission is used here. In addition, the optimum decoding technique is the Minimum Mean Square Error (MMSE) estimation method. Hence, in order to estimate the event information, \(S_i\), the MMSE estimation is applied for \(Y_i\) readings. Let \(Z_i\) denote this estimation process. And \(Z_i\) can be defined through a linear transformation, i.e., \(Z_i=aY_i\). Here, the scaler a can be determined by solving \(\partial E[(S_i-aY_i)^2]/\partial a=0\). Then \(Z_i\) can be determined as

$$\begin{aligned} Z_i=\frac{E[S_i Y_i]}{E[Y_i^2]}Y_i=\frac{\alpha _i ~ \sigma _S^2}{P_i+\sigma _W^2}Y_i. \end{aligned}$$
(14)

Then, the estimated version, \(\hat{S}\), of the original event source, S, can be computed by using the estimations of the event readings, i.e., \(Z_i\) \(i \in \{1,2,\ldots ,M\}\), as follows

$$\begin{aligned} \hat{S}=\frac{1}{M}\sum _{i=1}^{M}Z_i. \end{aligned}$$
(15)

Finally, the distortion \(D_{point}\) of the single-hop communication can be computed by

$$\begin{aligned} D_{point}=E[(S-\hat{S})^2]. \end{aligned}$$
(16)

By substituting both (14) and (15) in (16), then \(D_{point}\) is given as follows

$$\begin{aligned} D_{point}& {}= \sigma _S^2-\frac{\sigma _S^4}{M}\sum _{i=1}^{M}\frac{P_i}{P_i+\sigma _W^2}(2 \rho (S,S_i)-(1/M))+ \nonumber \\&+ \frac{\sigma _S^6}{M^2}\sum _{i=1}^{M}\sum _{j\ne i}^{N}\frac{\alpha _i^2\alpha _j^2 \rho (S_i,S_j)}{(P_i+\sigma _W^2)(P_j+\sigma _W^2)}, \end{aligned}$$
(17)

where both \(\rho (S,S_i)\) and \(\rho (S_i,S_j)\) are the correlation coefficients, between event S and node i, and between node i and node j, respectively. Both these correlation coefficients are computed by using (10). The distortion function \(D_{point}\) depends on the statistical behaviour of the sources and noises. Also, the distortion indicates how accurate the original event, S, can be estimated at the BS for the single-hop communication model.

4.2 Distortion for Two-Hop Communication Model

The two-hop communication model is presented in Fig. 3. In this model, there are r number of clusters,\(\;k\in \{1, 2, \ldots ,r\}\). In each cluster k, there are one Cluster Head (CH), \(CH_k\), and \(m_k\) number of Cluster Members (CMs),\(\;i\in \{1, 2, \ldots ,m_k\}\). Each CM i in the cluster k, \(CM_{k,i}\), forwards its readings to its associated \(CH_k\). Then, \(CH_k\) aggregates and reports to the BS. Note that the selection of the CMs and CHs will be introduced in the next subsection. The main aim of BS is to estimate the event source, S, based on the observations of the CMs, i.e., \(S_{k,i}\), which is the event signal at the location of the \(CM_{k,i}\). Due to the observation noise, \(CM_{k,i}\) observes the noisy version, \(X_{k,i}\), of the event signal, \(S_{k,i}\), as given below

$$\begin{aligned} X_{k,i}=S_{k,i}+N_{k,i} \end{aligned}$$
(18)

where the samples of \(N_{k,i}\) are modelled as a set of i.i.d. Gaussian random variables with zero mean and variance \(\sigma _{N}^2\). Also, the samples of \(S_{k,i}\) are modelled according to the jointly Gaussian random variables with zero mean and variance \(\sigma _S^2\). These characteristics are assumed to be the same for all clusters. In order to forward the noisy observations, \(X_{k,i}\), to the BS, each \(CM_{k,i}\) send its readings to its associated \(CH_k\) through the channel with the noise term \(W_{k,i}\). Then, the received samples of \(Y_{k,i}\) can be defined as

$$\begin{aligned} Y_{k,i}=\alpha _{k,i}X_{k,i}+W_{k,i}, \end{aligned}$$
(19)
Fig. 3
figure 3

Two-hop communication model

Full size image

where the samples of \({W}_{k,i}\) are modelled asa set of i.i.d Gaussian random variable with zero mean and variance \(\sigma _W^2\). Here, similar to (13), the constant \(\alpha _{k,i}\) is employed to satisfy the power constraint of the transmission and given by

$$\begin{aligned} \alpha _{k,i}=\sqrt{\frac{P_{k,i}}{\sigma _S^2+\sigma _N^2}} \end{aligned}$$
(20)

where the denominator represents the power of \(X_{k,i}\) and the numerator is the power constraint of \(CM_{k,i}\). Each \(CH_k\) uses the received sample, i.e., \(Y_{k,i}\), to estimate the event signal \(S_{k,i}\) by following the MMSE estimation as explained in Sect. 4.1. \(Z_{k,i}\) denotes the estimation and given by

$$\begin{aligned} Z_{k,i}=\frac{\alpha _{k,i}\sigma _S^2}{P_{k,i}+\sigma _W^2}Y_{k,i} \end{aligned}$$
(21)

Furthermore, \(CH_k\) averages all of \(Z_{k,i}\; i\in \{1,\ldots ,m_k\}\) to produce the event information \(S_k\) to transmit as follows

$$\begin{aligned} S_k=\frac{1}{m_k}\sum _{i=1}^{m_k}Z_{k,i}. \end{aligned}$$
(22)

Then, \(CH_k\) sends \(S_k\) to the BS over a channel given below

$$\begin{aligned} Y_k=\alpha _k S_k+g_k \end{aligned}$$
(23)

where \(Y_k\) stands for the samples received by the BS, and \(g_k\) is a channel noise modelled as i.i.d Gaussian random variables with zero mean and variance \(\sigma _g^2\). The constant \(\alpha _k\) is again used to satisfy the power constraint and can be introduced as

$$\begin{aligned} \alpha _k=\sqrt{\frac{P_k}{E[S_k^2]}}=\sqrt{\frac{P_k}{\sigma _{S_k}^2}} \end{aligned}$$
(24)

Notice that \(S_k\) has zero mean and then, its power is equal to its variance, i.e., \(\sigma _{S_k}^2\). By substituting (22) into (24), \(\alpha _k\) can be represented as

$$\begin{aligned} \alpha _k=\sqrt{\frac{P_k m_k^2}{\sum _{i=1}^{m_k}\frac{\alpha _{k,i}^2\sigma _S^4}{P_{k,i}+\sigma _W^2}(1+\sum _{j\ne i}^{m_k}\frac{\alpha _{k,j}^2 \sigma _S^4 \rho (S_{k,i}S_{k,j})}{P_{k,j}+\sigma _W^2})}} \end{aligned}$$
(25)

where \(\rho (S_{k,i},S_{k,j})\) is correlation coefficient between both \(S_{k,i}\) and \(S_{k,j}\). Upon receiving the samples for the CHs, the BS is then tries to estimate the samples at block D, i.e., \(S_k\), through the MMSE estimator as

$$\begin{aligned} Z_k=\frac{\alpha _{k}\sigma _{Sk}^2}{P_{k}+\sigma _g^2}Y_{k}. \end{aligned}$$
(26)

where \(Z_k\) denotes the estimation of \(S_k\). Finally, by incorporating the estimated samples \(Z_k,\;k \in \{1,\ldots ,r\}\), the estimated version of the event signal is obtained as

$$\begin{aligned} \hat{S}=\frac{1}{r}\sum _{k=1}^{r}Z_k. \end{aligned}$$
(27)

The distortion function associated with this final estimation, i.e., \(D_{relay}\), and it can be calculated in the MMSE sense as

$$\begin{aligned} D_{relay}=E[(S-\hat{S})^2]. \end{aligned}$$
(28)

In the derivation of \(D_{relay}\), the noise terms \(g_k\), \(N_{k,i}\) and \(W_{k,i}\) are assumed to be independent and hence uncorrelated. Then, by substituting both (26) and (27) into (28), \(D_{relay}\) is calculated to be represented as

$$\begin{aligned} D_{relay}= & {} \sigma _S^2-\frac{1}{r^2}\sum _{k=1}^{r^2}\frac{P_k}{P_k+g_k}\frac{1}{m_k^2} \sum _{i=1}^{m_k}\frac{\alpha _{k,i}\sigma _S^2}{P_{k,i}+\sigma _W^2} \times \nonumber \\&\times \left( 2r m_k \rho (S,S_{k,i})-1-\sum _{j \ne i}^{m_k}\frac{\alpha _{k,j}\sigma _S^2}{P_{k,j}+\sigma _W^2}\right) + \nonumber \\&+\frac{1}{r^2}\sum _{k=1}^{r}\sum _{l\ne k}^{r} \frac{{P_k P_l}/{m_k m_l}}{(P_k+\sigma _g^2)(P_l+\sigma _g^2)} \times \nonumber \\&\times \sum _{i=1}^{m_k}\sum _{j\ne i}^{m_k}\frac{\alpha _{k,i}\alpha _{k,j}\sigma _S^6}{(P_{k,i}+\sigma _W^2)(P_{l,j}+\sigma _W^2)} \rho (S_{k,i},S_{l,j}) \end{aligned}$$
(29)

4.3 The Operations of EDC Algorithm

In this section, by employing the vector quantization (VQ) [18], how the EDC algorithm determines and eliminates inessential sensor nodes is introduced. As well as, how the EDC algorithm forms the clusters is discussed. In particular, it employs the K-means clustering algorithm, with respect to single-hop and two-hop distortion constraints. The K-mean is a method of vector quantization and attractive for image processing applications [19]. In the next two subsections both node elimination and clustering are explained.

4.3.1 Node Elimination

In this part, node elimination is explained with to respect to K-means clustering method [20] and single-hop distortion level. The K-mean clustering algorithm is popular technique for image processing. The correlated pixels can be selected by exploiting this clustering technique. From the viewpoint of WSNs, the K-means clustering algorithm can be used to exploit the spatial correlation among the sensor nodes. This is done by considering both, the locations of these sensors and the derived single-hop distortion from Sect. 4.1, as an input to the algorithm [8]. Then, the algorithm maps the two-dimensional input vectors (i.e., two-dimensional vector that represents the locations of the sensor nodes) into a set of vectors called codewords. Furthermore, the set of codewords is called as codebook. Those codewords are vector of two-dimensional locations of the centroids. The sensor nodes that are the closest to the locations of these centroids are called as unrepresentative nodes while the other remaining nodes are referred as representative nodes. These unrepresentative nodes are the eliminated ones, i.e., nodes are not required to sense the environment. Both representative and unrepresentative nodes are defined iteratively using k-mean clustering with respect to the single-hop distortion constraints.

4.3.2 Clustering Formation

In this part, clustering formation is explained. In the previous part, k-mean algorithm is explained to find out both representative and unrepresentative nodes for given locations of sensor nodes and single-hop distortion constraints. In addition to these, this algorithm also defines the voronoi regions around these centroids to determine which region is belonged to each cluster. Furthermore, the EDC algorithm assigns CHs (cluster heads) role to the unrepresentative nodes and CMs (cluster members) role to the representative nodes. After the selection of the CHs, the K-nearest neighbours algorithm (K-NN) [21] is used to assign each CM to its \(k{\rm th}\) cluster. This is done by using the Voronoi diagram of the sensor field with respect to all locations of CHs. As a result, each Voronoi region represents one cluster, and it contains one CH and set of CMs. An example topology with the CHs, CMs and BS is illustrated in Fig. 4.

With EDC algorithm the representative nodes (i.e., CMs) should report their readings to the CHs to be aggregated and forwarded to the BS, according to the distortion constraints. And the CHs should not sense to save its energy. In the single-hop scenario, the \(D_{point}\) is computed in the BS by step-wise increasing the number of representative nodes, which have sufficient energy and can report the event information, until the distortion constraint is satisfied. Similarly, in the two-hop communication scenario, the \(D_{relay}\) is computed by the BS by step-wise increasing the number of CMs with sufficient energy until the distortion constraint is satisfied. The number of CMs, which have sufficient energy and satisfy the distortion constraint, are determined as the essential nodes and the remaining nodes do not sense and become inessential. These inessential (i.e., unrepresentative nodes) are CHs or backup CHs. The backup CHs are unactive nodes.

As soon as the CMs satisfying the distortion constraint are determined, they start to sense and transmit their data to the associated CHs. Then, the CHs aggregate and forward the sensed event information to the BS for the final estimation of the event information. In case of one of the active CHs are running out of energy, it set to be unactive CH and one of the backup CHs is elected to be the active CH. In case of no existence of backup CH in current cluster, then one of CMs is elected to be the active CH with respect to two-hop distortion and energy constraints. In such a case, the distortion might be increase, because one of the essential nodes (i.e, CMs) is reduced by one. These CHs are still unactive until they get their energy back using RF energy harvesting.

Fig. 4
figure 4

Clustered network with Voronoi regions

Full size image

5 Performance Evaluations

In this section, the performance evaluations of the EDC algorithm are discussed. The simulation experiments are conducted in MATLAB. The performance is evaluated in terms of distortion, energy consumption rate and the network lifetime with and without energy harvesting.

Fig. 5
figure 5

The number of representative nodes versus distortion

Full size image
Table 1 Simulation parameters
Full size table
Fig. 6
figure 6

The number of alive nodes for 100\(\times\)100 \(m^2\) event area

Full size image
Fig. 7
figure 7

Distortion for 100 \(\times\) 100 \(m^2\) event area

Full size image
Fig. 8
figure 8

The number of alive nodes for 200 \(\times\) 200 \(m^2\) event area

Full size image
Fig. 9
figure 9

Distortion for 200 \(\times\) 200 \(m^2\) event area

Full size image
Fig. 10
figure 10

The number of alive nodes for 300 \(\times\) 300 \(m^2\) event area

Full size image
Fig. 11
figure 11

Distortion for 300 \(\times\)  300 \(m^2\) event area

Full size image

A total of 100 sensor nodes are assumed to be deployed randomly in \(100\times 100\), \(200\times 200\) and \(300\times 300\;m^2\) of event area by uniform distribution. Each sensor node is modelled to have an additional circuit for energy harvesting [16]. The BS is set to be located at the center of the event area. Furthermore, a cell tower is used as energy harvesting source, which is located also at the center of event area. Each node harvests and consumes energy based on the energy model, which is introduced in Sect. 3.3. One single antenna is used for transmission and receiving, and one for harvesting. The detailed simulation parameters are introduced in Table 1.

The EDC algorithm is first initiated to determine the representative and unrepresentative nodes. The determination is done by checking the single-hop distortion constraint. In Fig. 5, it is shown how the distortion is reduced by increasing the number of representative nodes. As observed from Fig. 5, after a specific number of representative nodes, the distortion can be no longer reduced even if the number of representative nodes is further increased. The results in Fig. 5 are obtained by taking the average over 100 trails. Then, as explained earlier, the EDC algorithm forms CMs, CHs, and backup CHs. This reveal that the EDC clustering algorithm can successfully eliminate the redundant nodes and form the clusters. In Figs. 6, 7, 8, 9, 10 and 11, without any consideration of energy harvesting, the performance of the EDC algorithm is given by comparing the single and two-hop communication models with respect to the number of alive nodes and the distortion. The comparisons are presented for three different environment size, \(100\times 100\), \(200\times 200\) and \(300\times 300\;m^2\). As observed, regardless of which environment size is considered, the two-hop communication model outperforms the single-hop model in terms of the number of alive nodes. This stems from the fact that the energy consumption increases exponentially with the communication distance and the two-hop model reduces the communication distance of the nodes by relaying the data over the cluster heads. This reveals that the two-hop communication model prolongs the network lifetime in comparison with the single-hop model. However, the single-hop model is better than the two-hop model in terms of the distortion since the two-hop model involves three noise terms (one sensing noise and two channel noise terms) while the single-hop model includes two noise terms (one sensing and one channel noise term).

In Figs. 12, 13, 14, 15, and 16, by enabling the sensor nodes to harvest their energy, it is shown that how the power level of the cell tower affects the performance of the EDC algorithm in terms of the distortion, energy consumption and the network lifetime. The power of the cell tower is changed as \(P_t=10,20,30\;Watt\). As observed, the EDC algorithm can successfully utilize the power level of the cell tower to improve the network lifetime time while keeping the distortion as low as possible.

Fig. 12
figure 12

Distortion for \(P_t=10 W\)

Full size image
Fig. 13
figure 13

Distortion for \(P_t=20 W\)

Full size image
Fig. 14
figure 14

Distortion for \(P_t=30 W\)

Full size image
Fig. 15
figure 15

Energy consumption for the different values of \(P_t\)

Full size image
Fig. 16
figure 16

Number of alive nodes for the different values of \(P_t\)

Full size image

6 Conclusion

The event distortion-based clustering (EDC) algorithm is proposed to exploit the spatial correlations among sensor nodes for the energy-efficient communication in energy harvesting WSNs. A theoretical framework of distortions for both single-hop and two-hop commutation models are derived, which are used to determine which nodes should report their readings to the BS. Furthermore, the performance evaluations of the EDC algorithm are discussed for the energy-harvesting sensor nodes. The results show that the two-hop communication model outperforms the single-hop communication model in terms of network lifetime. The two-hop model is simply having two links (i.e., two channels between the CMs and BS), and hence, higher distortion level is observed than one-hop model. Furthermore, it is shown that the EDC algorithm capability successfully utilize the energy harvesting such that the network lifetime can be improved as the power of the source (cell tower) increases. The consideration of more than two hops together with the derivation of the corresponding distortion functions are left for a future work.