1 Introduction

Log-periodic antennas are widely used because of their broadband characteristics in TV reception, electromagnetic compatibility measurements and wideband precision measurements. Log-periodic dipole arrays (LPDAs) present an almost flat gain over a wide operating bandwidth [1]. The gain of the antenna can be increased by increasing the number of dipoles [2]. LPDAs provide better front-to-back ratio but relatively lower gain than Yagi-Uda array antenna [3]. However, the LPDA has much larger bandwidth compared to Yagi-Uda antenna. Furthermore, the most important difference between the two antennas lies in their feeding patterns. Each dipole of LPDA is connected to the feeding source, whereas in Yagi-Uda antenna only one dipole is connected to the feeding source and all other dipoles are passive [4]. A very useful design procedure of LPDA has been proposed by Carrel [5, 6].

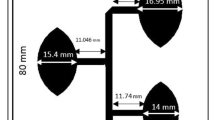
The LPDA is designed by using several dipoles of different lengths. In this way, each dipole operates in resonance condition at a certain frequency and this happens when the dipole length L is equal to half wavelength (λ/2). At the same time, dipoles with length greater or less than λ/2 at the same frequency act respectively as reflectors or directors, since they are away from their resonance condition. By employing dipoles of varying lengths, the LPDA is capable of operating effectively at a wide frequency range [4].

Figure 1 presents the basic geometry of a log-periodic dipole antenna. The LPDA consists of several parallel wire dipoles of varying lengths, which are arranged in a sequence so as to be included within the same angle 2α. The angle of intersection can be defined as:

$$\alpha = \tan^{ - 1} \left[ {\frac{1 - \tau }{4\sigma }} \right]$$
(1)

where τ is a scaling factor defined as the ratio of the lengths or diameters of two consecutive dipoles, as given by

$$\tau = \frac{{L_{n + 1} }}{{L_{n} }} = \frac{{d_{n + 1} }}{{d_{n} }}$$
(2)

and σ is a spacing factor constant defined by

$$\sigma = \frac{{s_{n} }}{{2L_{n} }}$$
(3)

where \(L_{n}\) and \(d_{n}\) are respectively the length and the diameter of the nth dipole, while \(s_{n}\) is the spacing between the nth dipole and its consecutive (n + 1)th dipole.The dipoles are connected to the feeding line in such a way that a phase reversal is obtained in the feeding between two consecutive dipoles [7]. In some LPDA designs, constant diameter dipoles are used to reduce cost [8]. The values of τ and σ are properly chosen by the user to design the antenna with predefined average directivity over the operating bandwidth, and this is done by using the well-known Carrel’s graph [5, 9, 10].

Fig. 1
figure 1

Log-periodic dipole array geometry

Full size image

2 Time Domain and Frequency Domain Simulation

The selection of the solver for the simulation of an antenna is a challenge for many researchers. There is no best suited solver for all types of applications. The time domain solver in the CST Microwave Studio (MWS) is based on the finite integration technique (FIT) describing Maxwell’s equations on a time-grid space whereas the frequency domain solver is based on the finite element method (FEM). The time domain method is more suitable for calculations over a wide frequency range because only one simulation is required and afterwards the frequency response is obtained through Fast Fourier Transform (FFT). Another interesting application of the time domain solver is that the calculation of the spectrum can be performed with an arbitrarily fine frequency resolution without any additional effort. Therefore, the time domain solver is more suitable for simulations of electrically large structures. The smaller the mesh cells are (more mesh cells), the longer the calculation time will be for this solver. The time domain solver in CST uses a hexahedral or a hexahedral transmission-line matrix (TLM) meshing technique for the simulation. The time domain simulation analysis is performed on a port-by-port basis.

On the other hand, when the frequency domain method is used, discrete simulations must be performed at discrete frequencies separated from each other by a specified frequency step to cover the entire operating bandwidth. Thus, adaptive refinement of the mesh at every frequency can be performed to obtain the results. The frequency domain simulation stops when the S-parameters converge. Nevertheless, a single simulation can provide results for all the ports in a single calculation. Therefore, the frequency domain solver finds its application in simulations of narrowband and electrically small structures. In CST, this solver uses either the hexahedral or tetrahedral meshing technique [11].

3 LPDA Measurments and Simulations

This study presents the measurement results of a ten-element LPDA conducted in open field conditions in 470–860 MHz frequency band (former analogue UHF TV band). The measurements are performed using a Rohde and Schwartz FSH8 portable spectrum analyzer. The gain of the antenna is measured using the reference antenna method with the help of calibrated biconical dipole antennas. A model of this antenna is developed in CST MWS 2016 to compare the simulation results with the measured results of the antenna. The simulation results obtained from CST MWS include the VSWR, realized gain and front-to-back ratio versus frequency. The realized gain of the antenna is defined as the difference between gain and mismatch loss of the antenna. The expressions for realized gain and mismatch loss are given below:

$$Mismatch\,Loss\,(dB) = - 10\,\log_{10} \left[ {1 - \left[ {\frac{VSWR - 1}{VSWR + 1}} \right]^{2} } \right]$$
(4)
$$Realized\,Gain\,(dBi) = Gain\,(dBi) - Mismatch\,loss\,(dB)$$
(5)

Furthermore, the optimization of this antenna has been performed in CST MWS by using Trusted Region Framework, Nelder Mead simplex algorithm, Classic Powell and Covariance Matrix adaptation evolutionary strategy (CMA-ES) included in this simulator.

Figure 2 presents an actual LPDA (left) and a designed model of the same LPDA in CST MWS (right). Both the antenna and its CST model include a short-circuited stub at their rear end. The CST model is discretized using hexahedral meshing with 564,435 cells. All simulations are performed with − 50 dB accuracy and with a port impedance of 50 Ω. The simulation of the antenna model is performed in time domain and frequency domain. Figures 3, 4 and 6 show respectively the comparative results of VSWR, realized gain and front-to-back ratio.

Fig. 2
figure 2

Actual ten-element LPDA (left) and LPDA model in CST MWS (right)

Full size image
Fig. 3
figure 3

Comparison between VSWR values derived from simulations in time and frequency domain. (Color figure online)

Full size image
Fig. 4
figure 4

Comparison between realized gain values derived from simulations in the time and in the frequency domain and open-field measurements (green line). (Color figure online)

Full size image

After this preliminary check of the antenna model, there is confidence that the results from time and frequency domain simulations are correct due to their good agreement. Also, the difference between the simulated and the measured realized gain is less than 0.5 dB in the frequency range of 490–860 MHz as shown in Fig. 5. Therefore, the CST model approximates with good accuracy the actual antenna. Optimization of this antenna is then performed using various optimization algorithms included in CST MWS.

Fig. 5
figure 5

Difference of simulated realized gain (time domain) and measured realized gain versus frequency

Full size image

4 LPDA Optimization

CST includes global optimizers and local optimizers. However, the search capability is larger in global optimizers compared to local optimizers. Trusted Region Framework (TRF), Nelder Mead simplex algorithm and Classic Powell algorithm are examples of local optimizers. On the other hand, CMA-ES is an example of a global optimizer.

In TRF optimizer, a linear model is created based on the primary data collected from a trust region around the starting point. The new model then acts as a new starting point until it converges to obtain an accurate model of the data. It is one of the most robust optimization algorithms offered by CST. TRF algorithm has a unique ability to predict improved fitness values by adjusting the limits and providing global convergence [12]. Nelder and Mead (in 1965) introduced Nelder Mead Simplex search algorithm, which is an improved version of the Simplex search algorithm proposed by Spendley, Hext and Himsworth in 1962 [13]. This algorithm utilizes multiple points, which are distributed across the parameter search space, so that the optimum value can be identified. It can be used as a solution for complex problem domains consisting of relatively few parameters. Classic Powell algorithm is considered to be a simple and robust optimizer, which can be used for a problem involving few parameters. The time of termination of the optimization process is decided by the accuracy requirement set before the start of the process. It is a relatively slow algorithm compared to other algorithms. However, it provides accurate results in some cases. CMA-ES is a self-adaptive evolution strategy and a global optimizer, which was developed by Hansen and Ostermeier, [14]. CMA-ES initializes strategy parameters like the number of variables, population size and their bounds in a well-defined fashion and thus does not require parameter tuning by the user [14, 15]. This algorithm is based on the evolution of a population of individuals. A comparison of CMA-ES with particle swarm optimization (PSO) is presented in [16]. CMA-ES solves a problem by generating a population of individuals using a Gaussian distribution [15, 17].

TRF algorithm, Nelder Mead simplex algorithm, Classic Powell and CMA-ES are used here to optimize the LPDA so that the antenna satisfies the requirements stated in Table 1. The half-dipole lengths (Ln/2), radius of the dipoles (rad), gap between the boom (gap), length of the boom (l_boom), width of the boom (b_boom), height of the boom (h_boom), length of the connector (l_connector) and spacing between the dipoles (sn) are the geometry parameters to be considered while performing optimization.

Table 1 Goals and weights for the antenna optimization
Full size table

The aim of the above-mentioned algorithms is to find the minimum value of a fitness function, so that all goals are satisfied. Therefore, the fitness function is constructed as a linear combination of the parameters to be optimized by taking into account the respective weights shown in Table 1. Then the global minimum of the fitness function is achieved by the algorithms by selecting proper values for the geometry parameters mentioned above. The optimized results of VSWR, realized gain and front-to-back ratio obtained with various evolutionary algorithms are shown respectively in Figs. 6, 7 and 8. In these figures, the results of the initial CST antenna model are also displayed.

Fig. 6
figure 6

Comparison between front-to-back ratio values (dB) derived from simulations in time and frequency domain. (Color figure online)

Full size image
Fig. 7
figure 7

Comparison between optimized and initial VSWR values

Full size image
Fig. 8
figure 8

Comparison between optimized and initial realized gain

Full size image

From Fig. 7, it is evident that the best performance in minimizing VSWR is obtained from TRF algorithm followed by the Nelder Mead Simplex algorithm. TRF algorithm is successful in minimizing VSWR to approximately 1.5. Other algorithms obtain VSWR values oscillating between 1.5 and 2. CMA-ES algorithm exhibits the poorest performance with the highest VSWR.

As shown in Fig. 8, the best optimizer of realized gain is again TRF algorithm since it produces a relatively flat realized gain approximately equal to 7.8 dBi. The other algorithms exhibit an average performance by obtaining a flat realized gain between 7 and 7.8 dBi above 550 MHz. Thus, an important improvement of approximately 1 dB is observed between the initial and the optimized realized gain by TRF algorithm in the frequency range of 670–750 MHz. On the other hand, the lowest realized gain is again obtained by CMA-ES algorithm.

In Fig. 9, CMA-ES algorithm seems to be the best performer in maximizing the front-to-back ratio above 20 dB followed by Nelder Mead Simplex algorithm and TRF algorithm. However, all algorithms have satisfactorily met the goal (> 20 dB) and show approximately similar front-to-back ratio, oscillating between 21 and 24 dB. The optimal LPDA dimensions derived from the above-mentioned optimizers and the initial antenna dimensions are shown in Table 2. The optimization algorithms have been configured to change the antenna dimensions only by ± 10% from their initial values.

Fig. 9
figure 9

Comparison between optimized and initial front-to-back ratio

Full size image
Table 2 LPDA geometry before and after optimization (dimensions in cm)
Full size table

5 Conclusion

The accurate modelling and simulation of a ten-dipole LPDA has been successfully performed using the time domain and frequency domain solvers of CST MWS. The simulated and practically measured results have been compared to ensure validity of the CST model. A comparative study of optimization of LPDA using various optimization algorithms included in CST MWS has been performed to obtain the best results for VSWR, realized gain and front-to-back ratio. TRF algorithm demonstrated the fastest convergence and achieved the best overall results with the best fitness function value.