1 Introduction

The increasing number of users of wireless communication systems forces the application of signals that efficiently make use of the available frequency bandwidth. The group of digital modulations producing a high spectral efficiency (SE) includes signals with CPM (Continuous Phase Modulation) [1]. In addition to good spectral properties, CPM signals are characterized by a constant envelope, so they can be generated by cheap, efficient, nonlinear amplifiers. CPM signals have been applied in GSM telephony, Bluetooth system, and satellite connections [2,3,4].

FDMA (Frequency Division Multiple Access) [2] is one of the techniques of band sharing between many users. In an FDMA system, each user is assigned one or more frequency channels, so that a few users can simultaneously transmit at the assigned frequencies. A drawback of FDMA is the necessity of using precise steep-slope filters both on the transmitter and receiver sides. The filters on the transmitter side determine the spectrum of the transmitted signal, so as to make it fit the band of the assigned channel, whereas the filters on the receiver side separate the channels and limit inter-channel interference (ICI). In order to increase the reliability and bit rate of telecommunication systems, the multi-antenna MIMO technique (Multiple Input Multiple Output) is used more and more often [5]. The technique involves multiple antennas on the transmitter and receiver sides. The advantages of the multiple-antenna solution consist in the benefits of diversification, collective reception and multiplexing [2, 5]. Employing the MIMO technique in telecommunication systems allows the use of Space–Time Codes (STC), improving transmission quality [6]. The group of STC codes includes Space–Time Block Codes (STBC) and Space–Time Trellis Codes (STTC). As compared to STBC codes, STTC codes introduce—in addition to the benefit of diversification—also the benefit of coding, but the decoding procedure in systems with STTC is more complex than STBC decoding [6].

Among the first significant works on the application of CPM signals in multiple-antenna systems were [7], [8] and [9] devoted to the combination of Constant Phase Modulation and Space–Time Coding. In [7] and [9], the authors presented the principles of structuring STC codes for CPM for a transmission via a quasi-statistical channel with fading, and for a small number of streams. In [8], they proposed a soft-decision algorithm for STC-CPM signal demodulation. At the transmission end, they used an interlaced system and an external convolutional encoder. The rules developed in [9] have been extended in [10] for the case of STC structure for CPM and a transmission via a channel with fast fading. [11] and [12] studied CPM signals encoded using the so-called orthogonal space–time codes based on Alamouti’s solution for linear modulations [13], i.e., on STBC (space–time block coding). This coding technique requires a simple receiver structure, but the complexity lies in obtaining orthogonal STC-CPM signals to ensure phase continuity of the encoded CPM signals, which consequently limits the practical use of this solution. This disadvantage is absent from the new class of orthogonal STC codes for CPM proposed in [14] and [15]. They are characterized by a low bit error rate attainable at a simultaneously low receiver complexity. Neither of the above solutions for MIMO transmission concerned multiuser CPM systems.

The literature has already discussed the aspects of increasing the spectral efficiency of systems employing CPM and FDMA (e.g., in [16]), but STC coding in multiuser scenario has not been taken into consideration. This paper presents the operation of an FDMA system using CPM signals combined with STC (STBC and STTC). We make the following assumptions: an FDMA-CPM system with a fixed and tight intercarrier frequency spacing is considered. Moreover, we allow each user to have individual phases and delays, resulting in an uplink assumption. Ideal power control is assumed, therefore the signal power at the receiver is equal for all users. We show that it is possible to obtain significant performance improvements using an iterative ICI cancellation technique and MMSE MIMO detector at the receiver.

The system performs transmission in an uplink connection. Using computer simulation, BER curves were determined in the function of E b /N0 for selected systems with STC CPM signals.

The paper is organized as follows. Section 2 presents a brief description of CPM signals. Section 3 describes STC coding. Section 4 presents the considered system. Section 5 provides the obtained simulation results. The paper is summarized and concluded in the final, sixth Section.

2 CPM Signals

The general equation describing CPM signals may be presented as follows:

$$x\left( {t,\alpha } \right) = \sqrt {\frac{{2E_{s} }}{T}} cos\left( {2\pi f_{0} t + \phi \left( {t,\varvec{\alpha}} \right) + \phi_{0} } \right)$$
(1)

where E s is the energy per symbol, T is the modulation interval, f 0 is the carrier frequency, ϕ 0 is the initial phase, and α = (…, α1, α0, α1, …) refers to a sequence of data symbols adopting one of the values from the set:

$$\alpha_{i} \in \left\{ { \pm 1, \pm 2, \ldots , \pm \left( {M - 1} \right)} \right\}$$
(2)

where M refers to modulation valence.

Phase ϕ(t,α), which carries information, may be described by the following equation:

$$\phi \left( {t,\alpha } \right) = 2\pi h\mathop \smallint \limits_{ - \infty }^{t} \mathop \sum \limits_{t = - \infty }^{\infty } \alpha_{i} g(\tau - iT)d\tau$$
(3)

where h is the modulation index defining the value by which the phase changes in each modulation interval. Function g(t) is a frequency impulse with duration LT. A frequency impulse may last for one modulation interval or longer. An impulse lasting only for the modulation interval (L = 1) classifies the system as a full response system, or otherwise (L > 1), the system is a partial response system. Apart from the frequency impulse duration, CPM signals are defined by modulation index h, modulation valence M and frequency impulse shape.

The shape of a frequency impulse is one of the parameters affecting the spectral properties of CPM signals. The most popular frequency impulses are: a rectangular impulse (REC), a raised-cosine impulse (RC), and a Gaussian-curve-shaped impulse. A rectangular impulse is characterized by a constant instantaneous frequency value and a linear change of phase in each modulation interval. Raised-cosine and Gaussian-curve impulses are characterized by better spectral properties (a strong concentration of the main lobe around the carrier frequency and a low level of side lobes) than the rectangular impulse.

Spectral properties of CPM signals also depend on the value of the modulation index defined as the ratio of two natural numbers. As modulation index h grows, the bandwidth increases, resulting in the deterioration of spectral properties.

3 STTC and STBC Encoding with CPM

The general structure of an STTC encoder is shown in Fig. 1 [6]. The encoder input data in each modulation interval t form a block of binary information described as:

Fig. 1
figure 1

Scheme of the STTC encoder

Full size image
$$c_{t} = \left[ {c_{t}^{1} ,c_{t}^{2} , \ldots , c_{t}^{m} } \right], m = log_{2} M$$
(4)

The encoder output in a given modulation interval is described by the sequence:

$$x_{t} = \left[ {x_{t}^{1} ,x_{t}^{2} , \ldots , x_{t}^{{n_{T} }} } \right]^{T}$$
(5)

where n T is the number of transmit antennas, and T denotes the transpose of the vector [·]. Each input sequence is fed to the shift register and multiplied by the coefficient of the encoder matrix. Finally, the STTC output signal for the i-th antenna and modulation interval t are described by the formula:

$$x_{t}^{i} = \mathop \sum \limits_{k = 1}^{m} \mathop \sum \limits_{j = 0}^{{v_{k} }} g_{j,i}^{k} c_{t - j}^{k}\,mod\,M, i = 1, 2, \ldots ,n_{T}$$
(6)

where \({\text{g}}_{{{\text{j}},{\text{i}}}}^{\text{k}}\) are generating matrix coefficients (k = 1, 2, …, m; j = 1, 2, …, v k ; i = 1, 2, …, n T ), m is the number of the encoder’s shift registers, v k is the number of memory cells of k-th shift register, and n T is the number of transmit antennas.

An STTC encoder can be described by means of a trellis which defines the output and the next state into which the encoder passes under the influence of input bits. The number of encoder states is determined by the equation:

$$n = 2^{v}$$
(7)

where v is the total number of memory cells for a given encoder.

An STBC-CPM system analyzed in this paper is based on Alamouti’s scheme [13].

The transmitted CPM signal vector can be expressed as it was shown in (5). The modified Alamouti scheme [13] with transmission matrix

$${\text{S}} = \left[ {\begin{array}{*{20}c} {s_{1} } & { - s_{2}^{*} } \\ {s_{2} } & {s_{1}^{*} } \\ \end{array} } \right]$$
(8)

is used in this paper for two transmit antennas FDMA CPM system. The signals transmitted by the first and second antennas into two time intervals are described by equations \(\varvec{x}_{1} = \left[ {s_{1} - s_{2}^{*} } \right]\) and \(\varvec{x}_{2} = \left[ {s_{2} s_{1}^{*} } \right]\) respectively.

4 System Description

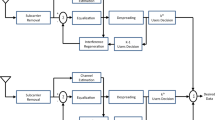
The present work considers the reception of CPM signals for a transmission in an uplink connection in an FDMA system employing the MIMO technique and STC coding. The studies were aimed at the evaluation of transmission quality in the system under analysis. Figure 2 shows a block diagram of the proposed system with STTC coding.

Fig. 2
figure 2

Block diagram of the MU STTC FDMA–CPM system

Full size image

At the input, each kth user binary information sequence \(\varvec{\alpha}_{0} , \ldots ,\varvec{\alpha}_{k - 1}\), is Convolutional Encoded (CE), interleaved (Int.) and converted into several (\(M_{T}\)) parallel streams in an STTC encoder. Each data stream is conveyed to one of \(M_{T}\) CPM modulators. A rate 1/3 systematic recursive CE with four states and good distance properties [17] has been chosen. Its connection polynomials (in octal notation) are (7; 5; 3)8, where 78 represents the coefficients of the feedback polynomial [18]. In order to achieve higher rates, the CE output is punctured as in [18]: a rate-matching algorithm is used to obtain an appropriate coding rate RC. The interleaver (Int.) is a symbol, spread (S-random) interleaver [19] with its parameters set according to the code word size.

Each user’s transmitter consists of an CE, interleaver, STTC encoder and a CPM modulator (Fig. 2). The efficiency of an STTC encoder depends on the number of transmit antennas. The STTC encoder considered in the paper uses two transmit antennas. Each user signal is characterized by a distinct phase \(\varphi_{k}\) and delay \(\tau_{k}\), as typically occurs in uplink systems. Ideal power control is considered here. As a result, the received signal power is equal for all users.

Figure 3 shows a block diagram of the proposed system with STBC coding. At the input, each kth user binary information sequence \(\varvec{\alpha}_{0} , \ldots ,\varvec{\alpha}_{k - 1}\) is convolutional encoded (CE), interleaved (Int.) and converted into two (\(M_{T}\), T = 2) parallel streams in an STBC encoder.

Fig. 3
figure 3

Block diagram of the MU STBC FDMA–CPM system

Full size image

In the analyzed system, a MIMO channel is considered. The system is composed of k users each of whom transmits signals via M T transmit antennas. The receiver uses M R antennas. The channel model used in the simulation takes into account multipath propagation. The channel model has been implemented as a Taped Delay Line (TDL) and it models a channel with flat fading and Additive White Gaussian Noise (AWGN) [5].

Each receive antenna receives a faded superposition of M T simultaneously transmitted signals corrupted by additive white Gaussian noise. The fading is assumed to be flat and distributed according to a Rayleigh pdf. The random path gains between transmit antenna m and receive antenna p, h m,p (t) are independent complex Gaussian random variables with zero mean and variance per dimension 1/2. The fading is slow, such that the \(M_{T} xM_{R}\) fading coefficients are constant during a frame, but vary from frame to frame. The AWGN noise components n p (t) are independent zero-mean complex Gaussian random processes with power spectral density N 0 .

At the receiving end, the system consists of a MIMO MMSE/STTC detector/decoder or MMSE/STBC detector/decoder and a low-complexity iterative algorithm to ICI cancellation [16].

With the assumption of uniform parameters of CPM, and an equal number of transmit antennas M T for each system user, the signal at the input of the p-th receiver antenna is described by:

$$r_{\text{p}} \left( t \right) = \mathop \sum \limits_{k = 0}^{K - 1} \mathop \sum \limits_{m = 0}^{{M_{\text{T}} - 1}} \mathop \sum \limits_{n = 0}^{B - 1} g_{k,m,n} \left( {t - n\tau_{k} ,\alpha_{k,m} } \right) \cdot e^{{j\left( {2\pi k\Delta_{f} t + \varphi_{k} } \right)}} + n_{p} \left( t \right),\quad j = 0, \ldots ,M_{\text{R}} - 1$$
(9)

where B is the number of intervals for which the STC—CPM signal is transmitted, for the analyzed in the paper system with STBC encoding B = 2.

The MMSE/STC block realizes the STC decoding and computes the cost function, i.e., minimizes:

$$G_{MMSE} = \sqrt {\frac{{n_{T} }}{{E_{s} }}} \left( {\varvec{H}^{H} \varvec{H} + \frac{{n_{T} N_{0} }}{{E_{s} }}I_{{n_{T} }} } \right)^{ - 1} \varvec{H}^{H}$$
(10)

where H is the matrix of channel impulse response estimates, I—identity matrix, N 0 —spectral density of noise power, upper index of quantity HH denotes the Hermitian transpose of matrix H and it is the sum of the operations of transpose and complex conjugate of the matrix. Signal y from MMSE/STC reaches the ICI cancellation block. The receiver carries out ICI cancellation through a set of single-user MAP detector/remodulator blocks, as described by Perotti et al. [16]. The remodulators make use of the output of the MAP detector to compute the remodulated signal s (i) k (t) relative to the kth user and ith iteration. The channel decoder performs two iterations loops. The inner loop is formed by the ICI canceller, the MAP detector, the CPE SISO decoder and the remodulator, while the outer loop involves the CPE SISO decoder, the CE SISO decoder, the interleaver and the deinterleaver between the inner CPE decoder and the outer CE decoder. ICI cancellation can be performed while executing the decoding iterations to enhance the receiver performance. In such a case, after the inner CPE decoder is executed, remodulation is performed. Then, interference cancellation is performed and the CPM receiver, including the inner CPE decoder, is again executed. The decoder starts decoding a received code word executing N IC inner iterations. Then, it executes N D times an outer iteration followed by an inner iteration. This way, ICI cancellation is performed as part of the decoding iterations and it results in an improved ICI cancellation [16]. On the final outer iteration, a decision is made on the transmitted data symbols \(\widehat{\varvec{\alpha}}_{0} , \ldots \widehat{\varvec{\alpha}}_{k - 1}\).

In the analyzed system, data are transmitted in blocks. The maximum number of transmitted bits is expressed by the following equation:

$$N = N_{Bits/Block} \times N_{Blocks} \times N_{Ch}$$
(11)

where N Bits/Block denotes the number of bits transmitted in a single block, N Blocks is the number of blocks, and N Ch is the number of channels in the system.

5 Simulation Results

By means of the Monte Carlo computer simulation, a bit error rate (BER) has been determined for the above described FDMA system with CPM modulation and STC (STTC and STBC) coding. The simulations have been performed with the aid of a simulation program written in C++ using IT++ libraries, ver. 4.2. The analysis assumed that each user transmits CPM signals with the same modulation and coding parameters, and of equal strength. It was assumed that the standardized value of the interval between the carrier frequencies of consecutive channels \(\Delta_{f} T\) in the system is equal to 3/4, and that the transmission is performed via four neighboring channels. The transmitted packages were 1000 bits long. The simulation was stopped if at least 100 errors occurred.

The analysis, for the FDMA-CPM system with STTC encoding, has been performed with reference to binary and quadrature CPM modulation with the parameters h = 1/2 and L = 1 and different shapes of the frequency impulse. The number of iterations in the receiver was experimentally fixed as a good trade-off between receiver performance and complexity. Two ICI cancellation iterations (NIC = 2) were performed before decoding, then four decoding iterations (N D  = 4) were performed. The CPM modulator was concatenated with a STTC encoder with generating matrices \(g1 = \left[ {0 2;2 0} \right]\) and \(g2 = \left[ {0 1;1 0} \right]\). The STTC encoder structure has been selected on the basis of the information provided in [6].

Figures 4 and 5 illustrate BER for the studied STTC systems. Based on the BER results obtained (Fig. 4), it may be stated that when transmission is performed for four users in parallel MSK (Gaussian frequency impulse (GAUSS), rectangular frequency impulse (REC) and rice cosine impulse (RC)) and with a reduced distance between subcarriers Δ f T = 3/4), the value E b /N 0 for BER at the level of 10−5 is higher in the range 0.5–1.5 dB than the E b /N 0 required by a system with a single user, i.e., in the case when ICI does not occur (no ICI, REC SU). Figure 5 also shows the so-called error background. It is determined for E b /N 0 from the value of about 3.5 dB and it results from the fact that the applied receiver does not completely eliminate ICI. Figure 5 presents BER for systems employing quadrature CPM modulation. In this case, each of the four users transmitted signals via two transmit antennas, and the receiver used four receive antennas. In this scenario, we observe that a E b /N 0 gain of 1 dB at BER = 10−5 is achieved for an ICI-free system compared to multiple-user systems. It should be noted that, like for MSK modulation, the so-called error background appears.

Fig. 4
figure 4

BER for STTC system (h = 1/2, M = 2, L = 1, Δ f T = 3/4), 4-users

Full size image
Fig. 5
figure 5

BER for STTC system (h = 1/2, M = 4, L = 1, Δ f T = 3/4), 4-users

Full size image

Figures 6 and 7 illustrate BER for the FDM-CPM systems with STBC encoding. Based on the BER results obtained (Fig. 6), it may be stated that when transmission is performed for four users in parallel MSK with a reduced distance between subcarriers Δ f T = 3/4 with ICI cancelation in the receiver, and two transmit and two receive antennas, the E b /N 0 at BER = 10−4 is higher about 1.3 dB than the E b /N 0 required by a system with a single user, i.e., in the case when ICI does not occur (no ICI, REC SU).

Fig. 6
figure 6

BER for STBC system (h = 1/2, M = 2, L = 1, Δ f T = 3/4), 4-users

Full size image
Fig. 7
figure 7

BER for STBC system (h = 1/2, M = 4, L = 1, Δ f T = 3/4), 4-users, with ICI cancelation and different numbers of receiver antennas

Full size image

Figure 7 presents BER for systems employing binary CPM modulation concatenated with STBC encoding for different numbers of receive antennas. In this case, each of the four users transmitted signals via two transmit antennas, and the receiver used one, two or four receive antennas. In this scenario, the E b /N 0 at BER = 10−4 obtained for the 2 × 2 system was worse than the one for the 2 × 4 system by about 2 dB and better than the one for the 2 × 1 system by about 3 dB.

Results show that proposed receiver with ICI cancellation technique improves the performance of multiuser MIMO CPM system.

6 Conclusions

In this paper, a multiuser STC FDMA-CPM system has been proposed. Through MMSE-based multiuser detection and low-complexity iterative ICI cancellation, considerable improvements in both BER are achieved with respect to single antenna systems, while the multiuser receiver complexity is kept low. A performance evaluation has been presented to demonstrate the superiority of the proposed multiuser FDM-CPM MIMO system. The study shows that it is possible to increase transmission efficiency by using CPM modulation and STC coding for MU transmissions, but the E b /N 0 at BER = 10−5 is higher than the one required for an ICI-free system by at least 0.5–3 dB for different CPM multiuser systems.