Blind Separation of Weak Object Signals Against the Unknown Strong Jamming in Communication Systems

Abstract

To obtain the mixed weak object signal against the super power signal (jamming) is still an challenging task in modern communication systems. In this paper, a novel framework is designed for weak object signal blind separation against the strong interference signal. To extract the strong interference signal,firstly, we separate the mixed signals with the optimized FastICA algorithm, then, an improved Interference Cancellation algorithm is proposed as reference signal based on the separated strong signal. Next, we separate the weak mixed signals by the improved FastICA algorithm again. Finally, we discuss the performance of the proposed method and verify the novel method based on several simulations. The experimental results demonstrate the effectiveness and robustness of the proposed method.

1 Introduction

In modern communication systems, the transmitted signals sometimes suffer from strong interferences, such as the multiple access interference (MAI) in a multi-user system or covert communication in the military systems (Fig. 1). Some scholars proposed interference rejection to solve the problem [1,2,3,4,5]. But few people mentioned that blind source separation based on weak signals against the strong interference signal.

Fig. 1

Covert communication in the military systems

In weak signals against the strong signal interference system, the components are composed of two parts: interference signal and mixed object signals. Since the interference signal is strong (strong interference signal) compared with the object signals (weak object signal), it is very difficult to obtain the weak object signals against the strong interference signal by using the classical blind source separation methods. Meanwhile, the classical blind source separation methods are lack of robustness. There are several existing algorithms that are partially related to the object signal detection, such as the Relax algorithm by Li etc [6], CLEAN technology by Sao etc. [7], FFT signal separation method by Gough [8] and FastICA algorithm by Hyvarinen etc [9,10,11]. Although these algorithms are partially related to the weak signal separation, their performances on passive communication system are still not sufficient for the practical applications. Hence, it is still necessary to develop more efficient object signal separation algorithm for the weak signal blind source separation against the strong interference. In this article, we proposed a novel method to separate the weak mixed signals against the strong interference. This method has a better separation performance and robustness than the traditional methods.

In [12], we first cancel the strong interference by using the Interference Cancellation algorithm (IC-algorithm), then, separate the mixed weak signals in Passive Radar System. The method has a good performance but has some limitations. It is only in the Passive Radar System, that is, the strong interference is known to us.

In this paper, an improved FastICA algorithm is proposed with the K-means clustering algorithm, which has lower complexity and better stability than classical FastICA method. By exploiting the separated strong signal, the channel parameters are estimated. From the above knowledge, a novel framework is designed for the weak object signal separation against the strong signal interference in the modern communication system. We first separate the mixed signals with the improved FastICA algorithm, then, an improved Interference Cancellation algorithm (IC-algorithm) is proposed based on the separated strong signal as reference signal. Next, we we separate the weak mixed signals by using the improved FastICA algorithm again. Finally, We verify the proposed method based on several simulations. The experimental results demonstrate the effectiveness of the proposed method.

The rest of the paper is organized as follows. In Sect. 2, we introduce the improved FastICA algorithm with K-means cluster and the Interference Cancellation algorithm (IC-algorithm). Section 3, we introduce the experimental process. In Sect. 4, we discuss the properties of the above method, including performance comparison, robustness analysis, complexity analysis, convergence analysis etc.. Finally, the conclusion is drawn in Sect. 5.

2 Blind Separation of Weak Signals Against the Strong Signal Interference

In this section, we introduce the blind separation of weak signals against the strong interference signal.

2.1 BSS Model

BSS aims at separating a set of N unknown sources from a set of M observations. Usually, the observations are obtained from M sensors, each sensor receives a mixture of those sources, the framework of BSS model is as below:

Fig. 2

Framework of BSS

The principle of BSS is shown in Fig. 2. The matrix $S(t)=[s_{1}(t),s_{2}(t),\ldots ,s_{N}(t)]$ is composed of N unknown sources, and the matrix $Y(t)=[y_{1}(t),y_{2}(t),\ldots ,y_{M}(t)]^{T}$ represents the separated (estimated) sources. Considering linear instantaneous mixtures model only, each observation is described as below:

$$\begin{aligned} y_{j}(t)=\sum \limits ^{N}_{i=1}a_{ij}s_{j}(t)+n_{i}(t), \quad j=1,2,\ldots ,M \end{aligned}$$

(1)

Here, $a_{ij}$ is the (i, j)th element of the mixed matrix, $n_{i}(t)$ is the ith component of the noise. Equation (1) can also be written in matrix form,

$$\begin{aligned} Y(t)=AS(t)+N(t) \end{aligned}$$

(2)

According to the relationships among the numbers of original signal (M) and the numbers of received antenna (N), blind source signals can be classified into overdetermined blind separation ($M<N$), determined blind separation ($M=N$) and underdetermined blind separation ($M>N$).

2.2 Framework of Blind Separation of Weak Signals Against the Strong Signal Interference

In this section, a novel framework based on the strong signal interference is designed for the weak object signal separation, which is shown in Fig. 3. We first separate the mixed signals with the improved FastICA algorithm, then, an improved IC-algorithm is proposed based on the separated strong signal as reference signal. Next, we separate the weak mixed signals by using the improved FastICA algorithm again. At last, we discuss the performance of the proposed method and verify the novel method based on several simulations.

Fig. 3

Framework of blind separation of weak signals under the strong signal interference

2.3 FastICA Algorithm

In this section, we separate each interesting object signals with the improved FastICA algorithm combined with k-means clustering.

The FastICA algorithm is a popular procedure for blind source separation. The size of the Gaussian character is usually measured by negative joint entropy, and can be written as [13]:

$$\begin{aligned} N_g(Y)=H(Y_{Gauss})-H(Y) \end{aligned}$$

(3)

where $Y_{Gauss}$ is the random variable with the same covariance and H(Y) is the formula for joint entropy calculation, which is defined as

$$\begin{aligned} H(Y)=-\int P_Y(\xi )\log P_Y(\xi )d\xi \end{aligned}$$

(4)

Here, $P_Y(\xi )$ is the joint probability density function. The detailed process of the FastICA algorithm can be concluded as follows:

• 1. Standardized data

• 2. Choose the original vector $W_0$ and set $\Vert W_0\Vert =1$

• 3. Select a non-quadratic function, e.g.,

  $$\begin{aligned} g_1(y)=\tanh (a_1y),\quad g_2(y)=y \exp \left( -\frac{y^{2}}{2}\right) ,\quad g_3(y)=y^{3} \end{aligned}$$

  (5)

• 4. Let

  $$\begin{aligned} W_p=E\{Zg(W_p^{T})\}-E\{g^{\prime}(W_p^{T})\}W_0 \end{aligned}$$

  (6)
• 5.
  $$\begin{aligned} W_p=W_p-\sum (W_p^{T}W_j)W_j,\quad j=1,2,\ldots ,p-1 \end{aligned}$$

  (7)
• 6.
  $$\begin{aligned} W_p=\frac{W_p}{\Vert W_p\Vert } \end{aligned}$$

  (8)

• 7. If $W_p$ is convergence, go to (8). Otherwise, return (4)

• 8. Let $p=p+1$, if $p\le m$, return (2).

Although FastICA algorithm is efficient, the performance heavily depends on selection of the initialization vector $W_0$. Here, we improve the original FastICA algorithm by using the K-means algorithm for setting $W_0$, which is introduced in the next section.

2.4 Improved FastICA Algorithm with K-Means Algorithm

As the above statement, the FastICA algorithm results depend on algorithm original vector $W_0$. However, in a blind context, it is hard to tell which original vector gives the best results, as the selection of the original vector is not a sufficient condition to have the optimal solution. We thus propose, for all sampling points, reduce the scope of the original vector with K-means clustering algorithm.

K-means has a rich and diverse history as it was independently discovered in different scientific fields by Steinhaus (1956) [14], Lloyd (proposed in 1957, published in 1982) [15], Ball and Hall (1965) [16], and MacQueen [17], it is the most popular and the simplest partitional algorithm.

K-Means algorithm aims to classify or to group out objects based on attributes or features into numbers of groups. Grouping is done by minimizing the sum of squares of distances between every datum and corresponding cluster center. The main steps of K-Means algorithm are as follows [18, 19]:

• 1. Give a cluster number K for starting;

• 2. Compute the squared Euclidean distance d from each object to each cluster and assign each object to the closest cluster;

• 3. Minimize Within-Cluster Sum of Squares (WCSS) in (9) and Update the cluster center for each cluster;

• 4. Re-calculate the squared Euclidean distance d based on the new memberships;

• 5. Repeat steps 3 and 4 until there is no possibility to move the objects to clusters.

Given a set of observations $(X_1,X_2,\ldots ,X_N)$ where each observation is a N-dimensional vector, the K-means clustering method aims to partition the N observations into K sets $(S_1,S_2,\ldots ,S_K)(K\le N)$ with regards to minimizing the function as [20]:

$$\begin{aligned} WCSS=\min \sum \limits ^{k}_{i=1}\sum \limits _{X_j \in S_i}\parallel X_j-\mu _i\parallel ^{2} \end{aligned}$$

(9)

where $\mu _i$ is the mean vector of $S_i$ cluster $i=1,2,\ldots ,K$.

Fig. 4

Primary data and the classification

Fig. 5

Cluster centers

The output of the K-means is the means vector $\mu _1,\mu _2,\ldots ,\mu _K$. The examples are shown in Figs. 4 and 5. It is seen that $\mu _i(i=1,2,\ldots ,K)$ is the cluster centers and stands for the general feature of the corresponding class. So, we choose the original vector $W_0$ in $\mu _1,\mu _2,\ldots ,\mu _K$.

From the above process, we can get the improved algorithm with the following optimizations:

• Reduce iteration times

  If the separation results are out of the acceptable range or the FastICA algorithm is non-convergent, we must replace the initial value. The improved FastICA algorithm reduces iteration times and improve the stability of the convergence.

• Improve the stability of the algorithm

  The original vector $W_0$ is in $\mu _1,\mu _2,\ldots ,\mu _K$, which have universality. Then, the process can improve stability of the algorithm.

2.5 Interference Cancelation Algorithm (IC-Algorithm)

After the introduction of improved FastICA algorithm, we next introduce our Interference Cancellation algorithm (IC-algorithm).

Due to the interference signal has very high power, and the object weak mixed signals are weak. So, we propose Interference Cancellation algorithm (IC-algorithm) to get rid of the jamming signal and obtain the weak object mixed signals.

Fig. 6

Framework of interference cancelation algorithm (IC-Algorithm)

The framework of the Interference Cancelation algorithm (IC-algorithm) is displayed in Fig. 6, where, $S_1+S_2+S_3+S_4$ is the original transmit signal. $S_1,S_2$ and $S_3$ are the weak object signals. $S_4$ is the separated strong jamming. $aS_1+bS_2+cS_3+dS_4+n$ are the received mixed signals of $S_1+S_2+S_3+S_4$ through the Gauss channel. Here,

$$\begin{aligned} a= [a_1,a_2,a_3,a_4],\quad b=[b_1,b_2,b_3,b_4], \end{aligned}$$

(10)

$$\begin{aligned} c= [c_1,c_2,c_3,c_4],\quad d=[d_1,d_2,d_3,d_4] \end{aligned}$$

(11)

Assume there are four observed signals, such as $l_1,l_2,l_3,l_4$, then we have

$$\begin{aligned} \left[ \begin{array}{c} l_1\\ l_2\\ l_3\\ l_4\\ \end{array} \right] = \left[ \begin{array}{cccc} a_1&{}b_1&{}c_1&{}d_1\\ a_2&{}b_2&{}c_2&{}d_2\\ a_3&{}b_3&{}c_3&{}d_3\\ a_4&{}b_4&{}c_4&{}d_4\\ \end{array} \right] \cdot \left[ \begin{array}{c} S_1\\ S_2\\ S_3\\ S_4\\ \end{array} \right] + \left[ \begin{array}{c} n_1\\ n_2\\ n_3\\ n_4\\ \end{array} \right] \end{aligned}$$

(12)

$dS_4^{\prime}+n^{\prime}$ in Fig. 6 is the reference strong jamming through the Gauss channel. Since $dS_4^{\prime}\gg n^{\prime}$, we obtain

$$\begin{aligned} \frac{d_iS_4^{\prime}+n_i^{\prime}}{d_jS_4^{\prime}+n_j^{\prime}}=\frac{\hat{d_i}}{\hat{d_j}}\approx \frac{d_i}{d_j},\quad i,j=1,2,3,4 \end{aligned}$$

(13)

Because the reference strong jamming has been separated with the above improved FastICA algorithm, we are able to estimate the channel parameters with the reference strong jamming firstly. Then, the strong interference signal can be separated from the mixed signal based on the channel parameters. This process can be represented as

$$\begin{aligned}&l_1-(l_1+l_2+l_3+l_4)\cdot \frac{\hat{d_1}}{\hat{d_1}+\hat{d_2}+\hat{d_3}+\hat{d_4}}\approx e_1S_1+f_1S_2+g_1S_3 \end{aligned}$$

(14)

$$\begin{aligned}&l_2-(l_1+l_2+l_3+l_4)\cdot \frac{\hat{d_2}}{\hat{d_1}+\hat{d_2}+\hat{d_3}+\hat{d_4}}\approx e_2S_1+f_2S_2+g_2S_3 \end{aligned}$$

(15)

$$\begin{aligned}&l_3-(l_1+l_2+l_3+l_4)\cdot \frac{\hat{d_3}}{\hat{d_1}+\hat{d_2}+\hat{d_3}+\hat{d_4}}\approx e_3S_1+f_3S_2+g_3S_3 \end{aligned}$$

(16)

$$\begin{aligned}&l_4-(l_1+l_2+l_3+l_4)\cdot \frac{\hat{d_4}}{\hat{d_1}+\hat{d_2}+\hat{d_3}+\hat{d_4}}\approx e_4S_1+f_4S_2+g_4S_3 \end{aligned}$$

(17)

Hence, we obtain the mixed useful signal $Y_1,Y_2,Y_3$, and

$$\begin{aligned} \left[ \begin{array}{c} Y_1\\ Y_2\\ Y_3\\ \end{array} \right] = \left[ \begin{array}{ccc} e_1&{}f_1&{}g_1\\ e_2&{}f_2&{}g_2\\ e_3&{}f_3&{}g_3\\ \end{array} \right] \left[ \begin{array}{c} S_1\\ S_2\\ S_3\\ \end{array} \right] \end{aligned}$$

(18)

We can see, the strong interference signal has been cancelled by (2)–(10). Finally, we obtain the mixed object signals denoted as $e\hat{S_1}+f\hat{S_2}+g\hat{S_3}+\hat{n}$.

3 Simulation and Blind Source Signal Separation Results

In this section, we verify the proposed method. We first introduce the parameter setting used in our experiments. We set the sample rate as $fb=2*10^{4}$ Hz, the transmission bit rate as $fb=10^{3}$bps, the modulation frequency as $f_0=2*10^{3}$Hz, the bit numbers as $m=80$, and the original signal numbers as $MK=4$.

3.1 Effectiveness of Interference Cancellation algorithm (IC-Algorithm)

In Fig. 7, we further display the result of the strong separated interference signal channel parameter estimation error under different $S_{q}/N_{o}$, here $S_{q}/N_{o}$ is the radio of the strong interference signal and background noise, where the computational formula is composed of two steps [21]:

• 1. Vector Standardization, Suppose the vector is $a=(a_1,a_2,a_3)$, the standardization vector is

  $$\begin{aligned} \frac{a}{\parallel a\parallel }=\left( \frac{a_1}{\parallel a\parallel },\frac{a_2}{\parallel a\parallel },\frac{a_3}{\parallel a\parallel }\right) \end{aligned}$$

  (19)

• 2. Error function,

  $$\begin{aligned} Error=\left\| \frac{\hat{a}}{\parallel \hat{a}\parallel }-\frac{a}{\parallel a\parallel }\right\| _2 \end{aligned}$$

  (20)

  where $\hat{a}=(\hat{a_1},\hat{a_2},\hat{a_3})$ is the estimation of $a=(a_1,a_2,a_3)$.

It is seen that the Error becomes small along with the increase of $S_{q}/N_{o}$, which demonstrates the channel characteristic and the effectiveness of our Interference Cancellation algorithm (IC-algorithm). The algorithm is proposed in Algorithm 1.

Fig. 7

Channel parameter estimation error

3.2 Extracting the Strong Interference Signal with the Improved FastICA Algorithm

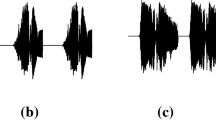
The sent source signals’ waveforms are shown in the Fig. 8. It is seen that the signal 1 is the strong interference signal, while signals 2–4 are the weak object signals. We aim to extract the strong interference signal from the sent source signal using the improved FastICA algorithm.

Fig. 8

Source signals’ waves. Signals 2–4 mixed weak signal waveforms. Signal 1 the strong interference signal

By the improved FastICA algorithm, we can get the strong interference signal. The strong signal waveform is shown in Fig. 9.

Fig. 9

The extracting strong interference signal from the sent source signal

3.3 Strong Interference Signal Cancelation Using the Interference Cancelation Algorithm (IC-Algorithm)

After getting the strong interference signal, we cancel the strong interference signal from the original mixed signal by using the Interference Cancellation algorithm (IC-algorithm). The separated weak signal waveforms are displayed in Fig. 10.

Fig. 10

The mixed signal after remove the super power signal component

Fig. 11

The separated weak signal using the improved FastICA algorithm

3.4 Blind Signals Separation with the Improved FastICA Algorithm

After transitions from the Gauss channel, the received mixed signal waveforms are shown in Fig. 10 (Received Composite Signal). Here, we consider four channels to fully simulate the realistic signal transmission, which are shown from top row to the bottom row in Fig. 10, respectively.

The final blind source separation waveform (the interested object signal) are shown in Fig. 11 by the proposed improved FastICA. The three signals are displayed respectively. It is seen that the obtained three object signals are very similar to the initial object signals compared with the signals in Fig. 8. The algorithm is proposed in Algorithm 2.

4 Discussions on the Properties

4.1 The First Comparative Experiment of Effect

We compare the signals between Figs. 8 and 11 with objective evaluation and further compare the separation performance with the classical FastICA algorithm [13]. The Pearson’s correlation coefficient value is used. The results are shown in Fig. 12, where Pearson’s correlation coefficient is defined as

$$\begin{aligned} r=\frac{\sum ^{n}_{i=1}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum ^{n}_{i=1}(x_i-\bar{x})^{2}\sum ^{n}_{i=1}(y_i-\bar{y})^{2}}} \end{aligned}$$

(21)

Fig. 12

Blind source separation result, this article method has a better performance than classical FastICA algorithm

We can see that blind sources signals can be efficiently separated with the proposed method and it has a better performance than the classical FastICA algorithm.

4.2 The Second Comparative Experiment of Effect

From the above section, we can know the method has a satisfying separation effect. In the following section, we will analyse the separation effect by using the performance error analysis as another evaluation criterion. In the error performance analysis, we further compare the separation performance with the classical JADE Algorithm [22], and the PI value is used. The formula is defined as:

$$\begin{aligned} PI=E\left\{ \frac{\parallel A \parallel -\parallel \widehat{A}\parallel }{\parallel A \parallel }\right\} , \end{aligned}$$

(22)

here A is the mixed matrix, $\widehat{A}$ is the mixed estimation matrix.

Fig. 13

Blind source separation result, this article method has a better performance than classical JADE separation algorithm

From Fig. 13, we can see that it has a better performance than the classical JADE Separation Algorithm too.

4.3 Termination Criteria

Some stopping criteria are available such as monitoring the changes of the Coefficient Value defined in (21) or Performance Error in (22). Here we choose Performance Error in (22) to terminate the iterations when the overall updates of all the estimation mixed matrix $\widehat{A}$ are sufficiently close to the original mixed matrix A. That is to say, we shall stop the iterations if the following inequality is met [23]:

$$\begin{aligned} \left\| \frac{\parallel A \parallel -\parallel \widehat{A}\parallel }{\parallel A \parallel }\right\| _{F} < \varepsilon , \end{aligned}$$

(23)

here $\widehat{A}$ is the estimation mixed matrix, and A denote the original mixed matrix. $\varepsilon$ and is a preset threshold (e.g., we use $\varepsilon =10^{-2}$ in experiments).

4.4 Robustness Analysis

After received the original mixed signals, we estimate the channel parameter.

$$\begin{aligned} \frac{d_iS_1^{\prime}+n_i^{\prime}}{d_jS_1^{\prime}+n_j^{\prime}}=\frac{d_i+\frac{n_{i}^{\prime}}{S_1^{\prime}}}{d_j+\frac{n_{j}^{\prime}}{S_1^{\prime}}},\quad i,j=1,2,3,4 \end{aligned}$$

(24)

From the above process, since $dS_4^{\prime}\gg n^{\prime}$, we can deduce the result as follows [21]:

$$\begin{aligned} \lim _{S_1 \rightarrow +\infty } \frac{d_i+\frac{n_{i}^{\prime}}{S_1^{\prime}}}{d_j+\frac{n_{j}^{\prime}}{S_1^{\prime}}}= \frac{d_{i}}{d_{j}} ,\quad i,j=1,2,3,4 \end{aligned}$$

(25)

Here, $S_1 \rightarrow +\infty$ is relative to base noise. Then, the above algorithm performance is not sensitive to base noise.

4.5 Complexity Analysis

The complexity of the introduced Interference Cancelation algorithm (IC-algorithm) can be specified by 2 parts [24].

• Estimate the channel parameters with the reference strong jamming.

  In (4), the coefficient matrix is $L\times K$, the source signal matrix is $K\times N$, then, the multiplicative complexity is $O(K \times N \times L)$, addition complexity is $O(K \times N \times L)$.

• Calculating the strong interference signal can be separated from the mixed signal based on the channel parameters.

From the Eqs. (6)–(9), we can get the received signal matrix is $L\times N$, the coefficient matrix is $L\times K$, the received signal addition matrix is $K\times N$, then, the multiplicative complexity is $O(K\times N\times L)$, addition complexity is $O(K\times N\times L)$.

So, the overall complexity can be determined as $O(K\times N\times L)$.

4.6 Convergence Analysis

In this subsection, we discuss the convergence of the proposed Interference Cancelation Algorithm (IC-algorithm). Due to the influence of the noise, the vector space $\widehat{\mathscr {L}}$ has a ambiguity. Obviously, the ambiguity will hamper the algorithm convergence due to the arbitrary vectors influencing the iterative process [25]. An convergence point is assumed to be unstable under the Interference Cancelation Algorithm (IC-algorithm) update rules if a small perturbation on the convergence procedure may cause the Interference Cancelation Algorithm (IC-algorithm) to diverge away from the convergence point [26]. However, these can be easily avoided if each iteration make $\parallel L_{i}-\widehat{L_{i}}\parallel$ minimize. The following statement discuss the convergence point of the Interference Cancelation Algorithm (IC-algorithm).

Theorem 1

Let $\widehat{\mathscr {L}} = \{\widehat{L_{1}},\widehat{L_{2}},\widehat{L_{3}},\widehat{L_{4}}\}$ denote the vector estimation space, then, for any initialization of the Interference Cancelation Algorithm (IC-algorithm), the limit $lim_{i \longrightarrow \infty }$ exists, that is, the Interference Cancelation Algorithm (IC-algorithm) converges [27].

Proof

Construct monotonic increasing sequence $(L_{1n},L_{2n},L_{3n},L_{4n})\in \widehat{\mathscr {L}}$. The sequence has an upper bound because the noise has a little disturbance. Then, we have $\forall \varepsilon >0,\exists N$, when $n>N$, $\mid \parallel (L_{1n},L_{2n},L_{3n},L_{4n})\parallel -\parallel (L_{10},L_{20},L_{30},L_{40})\parallel \mid <\varepsilon$, that is,

$$\begin{aligned} \lim _{n\rightarrow \infty } (L_{1n},L_{2n},L_{3n},L_{4n})=(L_{10},L_{20},L_{30},L_{40}). \end{aligned}$$

(26)

From the above procedure, we proves the convergence of the proposed Interference Cancelation Algorithm (IC-algorithm). $\square$

5 Conclusions

In this paper, we propose a novel blind source signal separation method. We first separate the mixed signals with the improved FastICA algorithm. Then, an improved Interference Cancelation Algorithm (IC-algorithm) is proposed based on the separated strong signal as reference signal. Next, we separate the weak mixed signals using the improved FastICA algorithm again. In the following, We verify the proposed method based on several simulations. The experimental results demonstrate the effectiveness of the proposed method. At last, we discuss the properties of the above method, including performance comparison, robustness analysis, complexity analysis, convergence analysis etc.