Abstract
The main drawback of channel models presented in the literature is the lack of physically justified integration of all basic phenomena such as fluctuations, channel dispersion, and selective fading that occur in the actual radio channels. Based on physical premises, presented in this paper, the developed channel model reproduces all basic phenomena that affect the temporal, correlational–spectral, and spatial characteristics of the modelled radio channels. This effect is achieved by the structure of the model, which includes both the geometric channel model and statistical models of the received signal parameters. The geometry used in the model is based on the Parsons–Bajwa multi-elliptical model and the relationship, which describes the Doppler frequency as a function of the spatial position of object. Therefore, this model is called the Doppler multi-elliptical channel model (DMCM). The source of input data that define the geometric and statistical parameters of the model is the power delay profile or the power delay spectrum. This makes sure that DMCM characteristics depend on the properties of the modelled propagation environment. A comparative analysis of the simulation results and the measurements that DMCM can correctly capture the actual transmission properties of real channels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Model of the communication channel is one of the basic elements of the algorithms used in simulation studies of wireless systems. Thus, a faithful representation of the transmission channel characteristics substantially affects the correctness of the test results.
The main group consists of models of the flat fading channels, which are applicable only to narrowband systems. In this case, the modelling procedure is reduced to generating multiplicative interferences with certain statistical properties that are described by probability density function (PDF) of envelope. This group should include the models of: Rayleigh [1], Rice [2, 3], Suzuki type I, and Suzuki type II [4, 5]. In addition to the above-mentioned models, extended models [6] are developed, which also take into account the relationship between the real and imaginary parts of the signal envelope. The differentiation of parameters of these parts leads to extended models of fast fading, examples of which are the following distributions: Weibull [7], Hoyt [8], Beckman [9], m-Nakagami [10], α–μ [11], κ–μ, and η–μ [12].
Modelling of the influence of the channel on wideband signals additionally requires considering differentiation in delays of particular components of the received signal or the channel dispersion, which results in the intersymbol interference (ISI) [2, 13]. In this case, the ISI channel model uses tapped delay line (TDL) [6], its coefficients are calculated on the basis of the channel impulse response. However, based on the TDL, the ISI channel models do not map the spatial properties of the multipath propagation, which cause selective fading. Therefore, in recent times, it is possible to notice the progressive development of geometric channel models (GCMs). These models are defined by spatial location of the transmitter, receiver, and scatterers that are described by the area form and the spatial density of their occurrence. The most commonly used forms of scattering areas are the circle [14–17], ellipse [16, 18, 19], ring [20], and semi-ellipse [21]. The most frequently used PDF of scattering density are the following distributions: uniform [15–21], Gaussian [18, 22, 23], hyperbolic [24], and inverted parabolic [14], as well as exponential and Rayleigh [25]. GCMs are used primarily to determine the characteristics describing the spatial properties of the signals, such as the PDF of the angle of arrival (AOA) and the power azimuth spectrum (PAS). The main difficulty in the practical application of these models is the matching problem of parameters to transmission properties of the environment. This is due to the lack of physical premises to select both shape and dimension areas as well the PDF of scatterer occurrence.
A brief overview of the radio channel models shows that obtaining temporal, correlational-spectral, and spatial characteristics of the received signals requires the use of different models with different input database. An additional difficulty is the matching problem of parameters to the transmission properties of the modelled propagation environment. Thus, we can observe that there is no model that can integrate all the phenomena occurring in the actual channel and provide a complete mapping of the channel characteristics based on the transmission properties of the environment. To meet this problem, the suggestion of such a channel model is presented in this study.
The developed model uses the statistical properties of the received signal parameters, the Parsons–Bajwa multi-elliptical model [26], and the relationship describing the Doppler frequency as a function of the spatial position of objects [27]. Therefore, this model is called the Doppler multi-elliptical channel model (DMCM) and is an extension of the ISI channel models. This extension takes into account the Doppler effect, which is conditioned by the current position and motion parameters of the objects. The input data for the model are: the spatial position and motion parameters of objects (transmitter/receiver), the power delay profile (PDP), or the power delay spectrum (PDS) that are related to the type of modelled propagation environment. In this study, the authors tried to present wide DMCM possibilities to represent the impact of the channel on the received signal characteristics in the time domain (the envelope as a function of time), the statistics of signal [cumulative density function (CDF), PDF of envelope], correlational properties [autocorrelation function (ACF) of envelope], frequency [power spectral density (PSD)], and space [power azimuth spectrum (PAS)]. Based only on the PDP or PDS and motion parameters of the transmitter/receiver, the developed model could provide all basic characteristics of the channel, which depend on the relative position of the objects. This fact proves the originality of DMCM, when compared with models presented in the literature.
The paper is organized as follows. Section 2 presents the origin and basic assumptions of DMCM. Section 3 describes in detail the GCM as well as the methodology for Doppler frequency shift (DFS) and AOA for delayed components of the received signal. Section 4 presents the statistical models of the received signal component parameters. For a simple scenario, wide DMCM possibilities for channel modelling are shown in Sect. 5. Verification of the model by comparative evaluation of the selected measurement results against the results obtained using DMCM is presented in Sect. 6. Lastly, Sect. 7 provides a summary that highlights the usefulness of the model for simulation tests.
2 Origin and Basic Assumptions of DMCM
The PDP and PDS are the basic characteristics, which, in practice, are the basis for the assessment of the transmission channel properties. In the literature [28–30], numerous measurements of these characteristics are presented, which indicate that the signal at the output of the channel has clusters structure in the time domain. Thus, the analytical description of the received band-pass signal y s (t) can be expressed in the following form:
where
is the received complex low-pass signal, L + 1 is the number of clusters with distinguishable delays, τ l (t) is the delay of propagation paths of the lth cluster (l = 0, 1, 2, …, L), K l is the number of propagation paths in the lth cluster, f 0 is the frequency of the carrier wave, r lk (t), ϑ lk (t), f Dlk (t) are the amplitude, phase, and DFS of the kth component in the lth cluster, respectively, s(t) is the complex envelope of the transmitted signal, \( \varphi_{lk} \left( t \right) = \vartheta_{lk} \left( t \right) - 2\pi f_{0} \tau_{l} \left( t \right) \), and n(t) is an additive channel interference.
Considering the nature of the propagation phenomena, the received signal can be represented as the sum of the three groups of components: the direct path component, the components of the local scattering, and the components coming to receiver with delays. It should also be noted that in most cases, the actual channels are wide sense stationary uncorrelated scattering (WSSUS). This fact is described inter alia in [2] and [13]. It follows that the parameters \( r_{lk} \left( t \right),\varphi_{lk} \left( t \right),f_{Dlk} \left( t \right) \) and τ l (t) can be described as random variables, which take constant values in finite time intervals, i.e. \( r_{lk} \left( t \right) = r_{lk} ,\varphi_{lk} \left( t \right) = \varphi_{lk} ,f_{Dlk} \left( t \right) = f_{Dlk} \), and τ l (t) = τ l . Hence, the expression that describes the complex low-pass signal and provides the basis for DMCM can be represented by
where r 0 and f D0 is the amplitude and DFS for the direct path component, respectively.
The above-mentioned expression shows that the statistical properties of the received signal depend on those of r lk and \( \varphi_{lk} \). It should also be noted that f Dlk , to a significant extent, depends on the statistical characteristics of AOA, i.e. on the geometry of the scattering area and the transmitter and receiver position. Therefore, the GCM is used to determine f Dlk . Thus, we see that both the statistical models of parameters and GCM, which maps the impact of the path reception direction at DFS, are an integral part of the developed model. Equation (3) and the above-mentioned considerations are the basis for the structure of DMCM, which is shown in Fig. 1.
As shown in Fig. 1, a fundamental difference between DMCM and models, which are based on the TDL, consists of introducing GCM to the structure of the model. In this way, DMCM provides a mapping of the properties of the received signal not only in the time domain and the spectrum, but also in space. The structure of the model shows that for the modelled propagation environment, the statistical properties of \( r_{lk} ,\varphi_{lk} \), and f Dlk have a significant impact on the accuracy of the estimation of channel characteristics. Therefore, the statistical models of these parameters and geometric model are defined on the basis of the PDP or PDS, which provide the mapping of actual channel properties.
3 GCM for Delayed Components
3.1 Origin and Basic Assumptions of the GCM
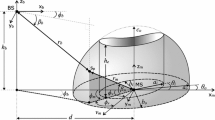
One of the essential components of the developed model is GCM. This element of DMCM is used to determine the AOA and DFS of components coming to the receiver with a delay. This GCM belongs to a class of two-dimensional (2D) models and is based on the multi-elliptical model of Parsons–Bajwa [26], which maps the spatial location of the scatterers, transmitter Tx, and receiver Rx. The spatial orientation of the geometric structure determines the location of the rectilinear trajectory of the object’s movement that marks the beginning of the coordinate system and the direction of the axis O0X0, as shown in Fig. 2. As can be seen from this figure, θ lk is the angle of departure (AOD), whereas α lk is the AOA of the kth propagation path for the lth ellipse.
A common focus of individual ellipses are determined by the positions of Tx, \( {\mathbf{x}}_{{\mathbf{T}}} = \left( {x_{{ 0 {\text{T}}}} ,y_{{ 0 {\text{T}}}} ,z_{{ 0 {\text{T}}}} } \right) \), and Rx, \( {\mathbf{x}}_{{\mathbf{R}}} = \left( {x_{{ 0 {\text{R}}}} ,y_{{ 0 {\text{R}}}} ,z_{{ 0 {\text{R}}}} } \right) \). The parameters of each ellipse are defined on the basis of individual cluster delays of the received signal according to
where \( a_{{{\text{E}}l}} \), \( b_{{{\text{E}}l}} \) are the semi-major and semi-minor axes of the lth ellipse, respectively, d is the distance between Tx and Rx, and \( {\text{c}} \) is the speed of light.
From relation (4), it can be noted that τ l is one of the basic DMCM parameters, because it determines the sizes of particular ellipses. The values of τ l and their amount (the number L) are determined on the basis of the PDP or PDS for which the base could provide the measurements or parameters of the standard channel models such as COST 207 [31] and WINNER [32]. When using the results of the measurements, L represents the amount of τ for which the PDP or PDS achieve local extremes.
The above-mentioned geometry makes it possible to assess the impact of the motion of objects in the changes of the DFS of the received signal components. If we assume a uniform velocity \( {\mathbf{v}} = \left[ {{\text{v}},0,0} \right] \) of Rx movement, its coordinates have the form of \( {\mathbf{x}}_{{\mathbf{R}}} = \left( {{\text{v}}t,0,0} \right) \), and the DFS of the signal reaching the Rx at the point with coordinates (x, y, z) is [27]
where \( f_{D\hbox{max} } = f_{0} {{\text{v}} \mathord{\left/ {\vphantom {{\text{v}} {\text{c}}}} \right. \kern-0pt} {\text{c}}} \) is the maximum DFS.
It should also be noted that any object trajectory can be approximated by straight sections, along which the object moves at constant speed. In this case, the parameters of the received signal are determined for each segment of movement in a coordinate system, the beginning of which defines one end of the segment and the direction of the coordinate x indicates the direction of velocity vector.
To simplify the spatial analysis of propagation phenomena, DMCM uses assumptions that constitute the basis for most of the previously developed GCMs.
-
1.
Propagation phenomena are considered only in a plane stretched on the velocity vector of the object and the line passing through the points where Tx and Rx are located (see Fig. 2).
-
2.
The radiation characteristics of the transmitting and receiving antennas are omnidirectional.
-
3.
The probability of propagation path is the same for each of the direction of departure wave, i.e. the probability of occurrence of a scatterer is the same for each direction when viewed from Tx.
-
4.
Each propagation path from Tx to Rx consists of scatterers on exactly one scattering element.
-
5.
Each scattering element is a reradiating omnidirectional element with the same scattering coefficient and uniform phase distribution.
3.2 Method of Determining AOA and DFS for Delayed Components
Equation (4), the geometry of the channel, and the assumptions make it possible to use the theory of images to determine the DFS and AOA of delayed components. The main input data of this method are the coordinates \( {\mathbf{x}}_{{\mathbf{T}}} \) and \( {\mathbf{x}}_{{\mathbf{R}}} \) of Tx and Rx, respectively, velocity vector \( {\mathbf{v}} \), and τ l of individual clusters. The method of determining AOA and DFS for delayed components is implemented by using the following steps:
-
the transformation of coordinate system;
-
the appointment of the coordinates of scattering element for the specified AOD;
-
the appointment of the coordinates of the apparent source;
-
the appointment of the AOA and DFS for the specified AOD.
Transformation of the coordinate system simplifies the analysis of the propagation phenomena in the plane spanned on \( {\mathbf{v}} \) and the line passing through the points Tx and Rx (see Fig. 2). This plane in the coordinate system O0X0Y0Z0 is described by the determinant
i.e. an equation in the form
A plane determined in this way is the basis for the creation of a new coordinate system OXYZ. The transformation of coordinates \( \left( {x_{ 0} ,y_{ 0} ,z_{ 0} } \right) \) of the system O0X0Y0Z0 to the OXYZ system is demonstrated by
where \( \begin{array}{*{20}c} {\beta_{0} = \arcsin \left( {{{z_{{0{\text{T}}}} } \mathord{\left/ {\vphantom {{z_{{0{\text{T}}}} } {\sqrt {y_{{0{\text{T}}}}^{ 2} + z_{{0{\text{T}}}}^{ 2} } }}} \right. \kern-0pt} {\sqrt {y_{{0{\text{T}}}}^{ 2} + z_{{0{\text{T}}}}^{ 2} } }}} \right)} & \wedge & {\beta_{0} = \arccos \left( {{{y_{{0{\text{T}}}} } \mathord{\left/ {\vphantom {{y_{{0{\text{T}}}} } {\sqrt {y_{{0{\text{T}}}}^{ 2} + z_{{0{\text{T}}}}^{ 2} } }}} \right. \kern-0pt} {\sqrt {y_{{0{\text{T}}}}^{ 2} + z_{{0{\text{T}}}}^{ 2} } }}} \right)} \\ \end{array} \) is the angle between the planes of O0X0Y0 and OXY or between axes O0Z0 and OZ.
In the new OXYZ system, the coordinates of Rx and Tx are \( \left( {x_{\text{R}} ,y_{\text{R}} ,z_{\text{R}} } \right) = \left( {{\text{v}}t,0,0} \right) \) and \( \left( {x_{\text{T}} ,y_{\text{T}} ,z_{\text{T}} } \right) = \left( {x_{{ 0 {\text{T}}}} ,y_{{ 0 {\text{T}}}} \cos \beta_{0} + z_{{ 0 {\text{T}}}} \sin \beta_{0} ,0} \right) \), respectively. Due to the above-mentioned coordinate system transformation, the problem of propagation modelling of the O0X0Y0Z0 space is reduced to modelling propagation on the OXY plane.
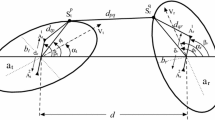
The transformation of the coordinate system to the middle of the section \( \overline{\text{TxRx}} \) (point O′ = E in Fig. 3) significantly simplifies the analysis of multipath propagation. Taking into account the coordinates of Tx and Rx, we can obtain the coordinates of point O′ = E
The transformation of the coordinates to the O′X′Y′ system with its beginning in point O′ = E consists of a shift of the OXY coordinate system by the vector \( {\mathbf{p}} = \left[ {x_{E} ,\,y_{E} } \right] \) and rotation by an angle β, as shown in Fig. 3. The angle β is determined by the direction of the \( {\mathbf{v}} \) of the Rx and a line defined by the position of the Rx and Tx, i.e. \( \begin{array}{*{20}c} {\beta = \arcsin \left( {{{\left( {y_{\text{T}} - y_{\text{R}} } \right)} \mathord{\left/ {\vphantom {{\left( {y_{\text{T}} - y_{\text{R}} } \right)} d}} \right. \kern-0pt} d}} \right)} & \wedge & {\beta = \arccos \left( {{{\left( {x_{\text{T}} - x_{\text{R}} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{\text{T}} - x_{\text{R}} } \right)} d}} \right. \kern-0pt} d}} \right)} \\ \end{array} \) where \( d = \sqrt {\left( {x_{\text{T}} - x_{\text{R}} } \right)^{2} + \left( {y_{\text{T}} - y_{\text{R}} } \right)^{2} } \) is the distance between Tx and Rx.
In the new O′X′Y′ system, the coordinates are given by
As shown in Fig. 3, in the O′X′Y′ system, the coordinates of the location of Tx and Rx, i.e. the foci of ellipses, are described by the following system of equations:
Based on the Parsons–Bajwa model, it has been assumed that the scattering elements are located on the ellipses. For a given AOD, θ lk , the coordinates \( \left( {x_{{{\text{Q}}lk}}^{\prime } ,y_{{{\text{Q}}lk}}^{\prime } } \right) \) of the scattering point Q lk are in line with the following system of equations:
where \( a_{{{\text{T}}lk}} = \tan \theta_{lk} \) and \( b_{{{\text{T}}lk}} = - x_{\text{T}}^{\prime } \tan \theta_{lk} \). The solution of this system of equations is
The apparent source method was used to determine the Doppler frequency f Dlk of the component of a signal coming from point Q lk . In Fig. 3, the source is designated as U lk . The determination of its coordinates consists of establishing the tangent l H of the ellipse at point Q lk , and then the perpendicular line l V to the tangent that passes through point Tx. These lines intersect at point V lk , which is located at the same distance from both Tx and U lk . This constitutes the basis for determining the coordinates \( \left( {x_{{{\text{U}}lk}}^{\prime } ,y_{{{\text{U}}lk}}^{\prime } } \right) \) of the apparent source.
The tangent l H of the ellipse at point Q lk is given by
where \( a_{Hlk} = - {{\left( {x^{\prime }_{{{\text{Q}}lk}} b_{{{\text{E}}l}}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {x^{\prime }_{{{\text{Q}}lk}} b_{{{\text{E}}l}}^{2} } \right)} {\left( {y^{\prime }_{{{\text{Q}}lk}} a_{{{\text{E}}l}}^{2} } \right)}}} \right. \kern-0pt} {\left( {y^{\prime }_{{{\text{Q}}lk}} a_{{{\text{E}}l}}^{2} } \right)}} \), \( b_{Hlk} = {{b_{{{\text{E}}l}}^{2} } \mathord{\left/ {\vphantom {{b_{{{\text{E}}l}}^{2} } {y_{{{\text{Q}}lk}}^{\prime } }}} \right. \kern-0pt} {y_{{{\text{Q}}lk}}^{\prime } }} \) and \( c_{Hlk} = {{a_{{{\text{E}}l}}^{2} } \mathord{\left/ {\vphantom {{a_{{{\text{E}}l}}^{2} } {x^{\prime }_{{{\text{Q}}lk}} }}} \right. \kern-0pt} {x^{\prime }_{{{\text{Q}}lk}} }} = - {{b_{Hlk} } \mathord{\left/ {\vphantom {{b_{Hlk} } {a_{Hlk} }}} \right. \kern-0pt} {a_{Hlk} }} \). The line l V perpendicular to the tangent (14) passing through point Tx is described by
where a Vlk = −1/a Hlk and \( b_{Vlk} = - a_{Vlk} x^{\prime }_{\text{T}} \).
Lines l H and l V intersect at one point V lk , and its coordinates \( \left( {x^{\prime }_{{{\text{V}}lk}} ,y^{\prime }_{{{\text{V}}lk}} } \right) \) are the solution of a system of Eqs. (14) and (15)
As the distance between points Tx and V lk , and V lk and U lk is the same, the coordinates \( \left( {x^{\prime }_{{{\text{U}}lk}} ,y^{\prime }_{{{\text{U}}lk}} } \right) \) of the apparent source U lk can be expressed as
In OXY system, the coordinates \( \left( {x_{{{\text{U}}lk}} ,y_{{{\text{U}}lk}} } \right) \) of the apparent source are determined based on (17) and reverse transformation of (10)
Hence, on the basis of relation (5), \( f_{D \, lk} \) of the signal component coming from point Q lk will be
The coordinates of the location of the apparent source U lk also provide the basis for determining α lk of signal arrival, namely,
The parameters described in (19) are the basis for the analysis of temporal and spectral, while those defined in (20) help to assess the spatial properties of the received signal.
4 Statistical Models of Received Signal Parameters
In addition to the GCM, the structure of DMCM also creates statistical models of the parameters of the received signal components. As can be seen from (3), one of the basic parameters of the received signal is r lk . According to
its PDF is determined based on the statistical properties of the power, p lk , of lkth received signal component. In DMCM, it is assumed that the statistical properties of p lk are described by a uniform distribution i.e.
where P l is the power determined on the basis of PDP or PDS.
The adoption of the above-mentioned statistics shows that the average power components of the lth cluster is equal to P l . Using relations (21), and (22), and the theorem on the function of the random variable [33], it is possible to determine the PDF of r lk
The above-mentioned relation forms the basis for determining the amplitudes of signal components generated in DMCM.
The power components reaching the receiver without delay is the sum of the direct component and components coming from local scattering. In this case, the power distribution is defined on the basis of Rice factor κ. The powers of the direct component and the local scattering components are described by P 0 κ/(1 + κ) and P 0/(1 + κ), respectively. Therefore, the amplitudes of local scattering components are determined on the basis of a PDF in the form
however, the amplitude of the direct component is constant, \( r_{0} = \sqrt {{{2P_{0} \kappa } \mathord{\left/ {\vphantom {{2P_{0} \kappa } {\left( {1 + \kappa } \right)}}} \right. \kern-0pt} {\left( {1 + \kappa } \right)}}} \). In the case of NLOS (non-line of sight) propagation, a direct component is not present; hence, we have κ = 0.
The statistical properties of \( \varphi_{lk} \) are associated with the phenomenon of scattering, which determines the properties of ϑ lk . Thus, the PDF of \( \varphi_{lk} \) determines Assumption 3 (Sect. 3.1), and the relationship 2πf 0 τ l ≫ 1 that has practical justification [13]. Hence, on the basis of the analysis presented in [9], for \( \varphi_{lk} \), uniform distribution is adopted
For local scattering components, the AOA is defined by statistical model. In this case, the PDF of α 0k is executed using von Mises’ distribution [34]
where I 0(·) is the zero-order modified Bessel function, β = α 0 and \( \beta \in \left( { - {{\pi }},{{ \pi }}} \right] \) is the angle between \( {\mathbf{v}} \) and the direction on the signal source, and γ is a coefficient characterizing the width of the AOA of the scattered components, i.e. the intensity of the presence of local scatterings.
The choice of γ value depends on the environmental conditions present in the surroundings of transmitting and receiving antenna and the direction of signal transmission. As shown in [34], for large scattering that occur in the vicinity of the omnidirectional receiving antenna, i.e. in an urban environment with low positioning of the antenna, γ is smaller than 3. In mobile radio systems, this case corresponds to downlink signal transmission. For uplink transmission, the angular scattering intensity of the received components is much smaller; hence, we assumed that γ > 10.
5 Signal Characteristics of DMCM for a Sample Scenario
A wide range of mapped phenomena, which occur in the real radio channels, determines the originality of the presented model. Therefore, in this section, using DMCM, the authors present the effects of channel on the transmitted signals in the range of temporal and their statistical properties, correlational-spectral, and spatial properties for a sample scenario. It should be noted that the purpose of this investigation is not to analyse the phenomena occurring in the radio channels, but to show a wide range of DMCM possibilities.
This section presents a set of characteristics obtained by DMCM, which is shown to be compatible with the characteristics of the signals occurring at the output of the real channel. This indicates that the developed DMCM maps a wide range of phenomena that are closely related to the specific propagation scenarios.
5.1 Simulation Scenario
The parameters of the test scenario and the associated PDP are the basis for a DMCM input data. The spatial position of objects (Rx/Tx), parameters of their movement, signal transmission direction, transmitter/receiver antennas surroundings, number of the scattering clusters, and associated delays are the basis for the definition of the following set of DMCM input data: \( \left( {x_{{ 0 {\text{T}}}} ,y_{{ 0 {\text{T}}}} ,z_{{ 0 {\text{T}}}} } \right) \), \( \left( {x_{{ 0 {\text{R}}}} ,y_{{ 0 {\text{R}}}} ,z_{{ 0 {\text{R}}}} } \right) \), \( {\mathbf{v}} \), κ, γ, L, P l , τ l , K l (l = 0, 1, 2, …, L). The results presented in this study are based on the measurement scenario presented in [29]. The choice of this scenario is dictated by the verification possibility of the selected simulation based on measurements results. The description of the scenario indicates that Rx moves in a uniform manner in a straight line at a constant velocity \( {\text{v}} = 50 \, {{\text{km}} \mathord{\left/ {\vphantom {{\text{km}} {\text{h}}}} \right. \kern-0pt} {\text{h}}} \), while Tx is located at a position with coordinates \( \left( {x_{{ 0 {\text{T}}}} ,y_{{ 0 {\text{T}}}} ,z_{{ 0 {\text{T}}}} } \right) = \left( {713.3, \, 9 8 3. 0, \, 20.0} \right){\text{ m}} \). The average distance between Tx location and Rx movement trajectory is 1200 m. The angle between the direction of Rx motion and the direction towards Tx is β = 55°. The heights of the receiving antenna and transmitting antenna in relation to street level are \( h_{\text{R}} = 2{\text{ m}} \) and \( h_{\text{T}} = 22{\text{ m}} \), respectively. The propagation conditions are the NLOS type (κ = 0), while local scatterings occurring around the receiver are omnidirectional (γ = 0). The number of clusters is L + 1 = 6, and the values of P l and τ l (0 ≤ l ≤ L), shown in Table 1, are assumed on the basis of the PDP.
Analysis of the results was carried out for a route with a length S = 50 m. On this route, the measurement sections (M = 8) were designated. For these sections, we assumed that the received signal parameters have fixed values. Based on [35], the length of each section was adopted to be 40λ, where \( \lambda \cong 0.16\;{\text{m}} \) is the wavelength, which results from the frequency of the transmitted signal (\( f_{ 0} = 1860\;{\text{MHz}} \)). Moreover, in simulation, the number of paths in each cluster was adopted to be K l = 10 (l = 0, 1, 2, …, L) and the sampling frequency of the signal was \( f_{s} \cong 200\,f_{D\hbox{max} } \cong 17.24\;{\text{kHz}} \), where \( f_{D\hbox{max} } = - f_{D\hbox{min} } \cong 86.1\;{\text{Hz}} \).
5.2 Analysis of the Signal Envelope
Figure 4 shows an example of the harmonic signal envelope received in conditions consistent with the adopted scenario.
An example graph of the signal envelope—Results based on simulations by using DMCM for the test scenario [29]
As indicated by theoretical analysis (e.g. [1, 2, 13]) and the results of empirical measurements (e.g. [36]), for NLOS conditions, the statistical properties of the envelope are described by the Rayleigh distribution. Accordingly, Fig. 5 shows a PDF of the signal envelope based on the data presented in Fig. 4. Statistical analysis of the data was carried out in MATLAB using the procedure ksdensity and with prior normalization of the signal in relation to its rms (root mean square).
PDF of the signal envelope corresponding to the data presented in Fig. 4
For comparison of the simulation and theoretical results, in Fig. 5, theoretical Rayleigh distribution, which is indicated by dashed line, is also presented. Figure 5 indicates a good fit of results obtained by using DMCM for the analysed example of data.
5.3 ACF and PSD
The methodology of determining the PSD is based on the Fourier transform with respect to the ACF of the signal generated in DMCM. In case of receiving independent components of the transmitted harmonic signal, its ACF, R x (τ), takes the form [13]
Figure 6 shows an example of the normalized module of ACF, |R x (τ)/R x (0)|, for which, the graph is obtained from (27) by using the results of DMCM simulation. The PSD, \( S_{x} \left( {f_{D} } \right) = {{\mathsf{F}}}\left\{ {R_{x} \left( \tau \right)} \right\} \), is designated based on the Wiener–Khinchin theorem, FFT (fast Fourier transform) procedure, and smoothing filtering. The extreme values of the PDS for f Dmax, f Dmin, and for the DFS associated with the angle between the direction of direct propagation path and direction of Rx motion (\( f_{D} \left( {\beta = 55^{ \circ } } \right) \cong 50{\text{ Hz}} \)) are the characteristic features of the graph presented in Fig. 7.
An example of the normalized module of ACF—Results based on simulations by using DMCM for the test scenario [29]
An example of the normalized PSD—Results based on simulations by using DMCM for the test scenario [29]
To facilitate graphical comparison of the simulations and measurement results, presented in Sect. 5, the normalized ACF and PSD of the extended Clake’s model (ECM) is also shown in Figs. 6 and 7. The ECM is defined by ACF, \( R_{\text{ECM}} \left( \tau \right) \), which, after normalization, takes the form [37]
where J 0(·) is the zero-order Bessel function of the first kind and B is the parameter of the ECM representing the inverse of received signal correlation time. The ACF and PSD of ECM, which are indicated by a dashed line, have been designated for B = 0.2 f Dmax according to [37].
Use of DMCM gives us the possibility to obtain the averaged characteristics. In this way, it is possible to assess the impact of spatial parameters on the PSD of the received signal. Figure 8 illustrates examples of the averaged PSDs for various angle β between the direction of Rx movement and direction towards Tx.
Examples of the normalized PSDs for different angle between the direction of the Rx motion and direction towards Tx—Results based on simulations by using DMCM for test scenario [29]
The above-mentioned graphs have been obtained for the scenario parameters, taking into account changes in β. As expected, we can observe that change in the PSD concentration is associated with β change, which follows from relation (19).
5.4 PAS
One of the fundamental characteristics, which describe the spatial properties related to the angular power distribution of the received signal power, is PAS. The methodology of estimating the PAS, P(ϕ), is based on histograms of the reception angle of signal components. In DMCM, for each cluster, the histogram i.e. the incidence of individual angles ϕ lk = α lk − β is determined. We can obtain estimator \( P_{\text{DMCM}} \left( \phi \right) \) as a sum of all histograms, which are normalized with respect to P l
where \( {\text{hist}}_{l} \left( {\phi_{lk} } \right) \) is a histogram obtained for lth cluster.
Figure 9 shows an example of PAS obtained for a single simulation procedure and a PAS obtained by averaging 100 simulations.
Sample and averaged PASs—Results based on simulations by using DMCM for the test scenario [29]
These characteristics describe the PASs of the received signals and can be used for the assessment of the spatial compatibility of devices and networks operating in a specified propagation environment. In DMCM, PAS methodology depends on the sizes of the ellipses, i.e. PDS, but not movement of the objects (Tx/Rx).
6 Verification of DMCM
A DMCM accuracy assessment was realized in relation to theoretical models available in the literature and empirical research carried out in urban environments. Statistical properties of the signal envelope (CDF and PDF), its ACF, PSD, and PAS were the basis for accuracy assessment of the developed model.
6.1 PDF and CDF of the Envelope
For the scenario described in Sect. 5, the obtained CDF and PDF of the signal envelope were used for accuracy evaluation of the mapping of Rayleigh fading in DMCM. The mean square error (MSE), δ 2, was adopted as an accuracy measure of the estimation of the characteristics. For the data presented in Fig. 4, the MSEs of CDF and PDF are \( \delta_{CDF}^{ 2} = 0.0 9\times 10^{ - 4} \) and \( \delta_{PDF}^{ 2} = 1. 1 9 \times 10^{ - 4} \), respectively. It can be observed that \( \delta_{CDF}^{ 2} \) is an order of magnitude smaller, when compared with \( \delta_{PDF}^{ 2} \). Therefore, the graphical comparison of the simulation and theoretical results is limited to the PDF because only in this case, we can observe clear differences in the graphs. The average values of \( \delta_{CDF}^{ 2} \) and \( \delta_{PDF}^{ 2} \) determined on the basis of averaging the results of a hundred simulation procedures are \( \overline{{\delta_{CDF}^{2} }} = \left( {0.25 \pm 0.2} \right) \times 10^{ - 4} \) and \( \overline{{\delta_{PDF}^{2} }} = \left( {2.31 \pm 1.29} \right) \times 10^{ - 4} \), respectively. Small values of these errors indicate correct mapping of the typical Rayleigh fading by DMCM.
6.2 PSD
A DMCM accuracy evaluation of the mapping of the spectral properties was carried out on the basis of a comparative analysis of the PSD obtained from simulations and measurements [29]. Figure 10 shows the PSD that was obtained as a result of empirical research. In Figs. 7 and 10, additional ECM graph is presented to facilitate graphical comparison of the results.
A comparative assessment of the results was carried out on the basis of the rms Doppler spread \( \sigma_{{f_{D} }} \), defined by
where \( F_{D} = {{\int_{{ - f_{D\hbox{max} } }}^{{f_{D\hbox{max} } }} {f_{D} S_{x} \left( {f_{D} } \right){\rm d}f_{D} } } \mathord{\left/ {\vphantom {{\int_{{ - f_{D\hbox{max} } }}^{{f_{D\hbox{max} } }} {f_{D} S_{x} \left( {f_{D} } \right){\rm d}f_{D} } } {\int_{{ - f_{D\hbox{max} } }}^{{f_{D\hbox{max} } }} {S_{x} \left( {f_{D} } \right){\rm d}f_{D} } }}} \right. \kern-0pt} {\int_{{ - f_{D\hbox{max} } }}^{{f_{D\hbox{max} } }} {S_{x} \left( {f_{D} } \right){\rm d}f_{D} } }} \). On the basis of the results of empirical studies, in [29] authors obtained \( \sigma_{{f_{D} }} = 60.3\,{\text{Hz}} \), while for a sample simulation test (results presented in Fig. 7), we obtained \( \sigma_{{f_{D} }} = 55.14\,{\text{Hz}} \). For a hundred simulation procedures, the average value was \( \overline{{\sigma_{{f_{D} }} }} = 55.29 \pm 1.70\,{\text{Hz}} \). A comparison of the results showed that the use of DMCM provides a relatively accurate representation of the Doppler spectrum in relation to the results obtained in real-world conditions.
6.3 PAS
A PAS is used to evaluate DMCM accuracy for the spatial power distribution estimation. In the literature, there is no description of measurements made for a certain scenario, which could provide all the basic characteristics of the signal at the channel output. Therefore, the accuracy assessment of the PAS estimation was conducted based on measurements [28], which were made under different conditions than those described in [29]. The measurements were carried out in typical urban (TU) areas (Aarhus, Denmark) and in bad urban (BU) areas (Stockholm, Sweden). On the basis of the description of the measurement campaigns [28], for the simulation research, a scenario in which Tx moves in a uniform manner in a straight line towards Rx (β = 0∘) was accepted. Rx was located at \( \left( {x_{{ 0 {\text{R}}}} ,y_{{ 0 {\text{R}}}} ,z_{{ 0 {\text{R}}}} } \right) = \left( {1508,\, 0,\, 1 9} \right)\,{\text{m}} \) for BU conditions and \( \left( {x_{{ 0 {\text{R}}}} ,y_{{ 0 {\text{R}}}} ,z_{{ 0 {\text{R}}}} } \right) = \left( {1508,\, 0,\, 3 0} \right)\,{\text{m}} \) for TU conditions. The average distance between Rx location and Tx movement trajectory was 1500 m. The heights of the transmitting antenna and the receiving antenna in relation to the street level were, respectively, \( h_{\text{T}} = 2\,{\text{m}} \) and \( h_{\text{R}} = 21\,{\text{m}} \) (for BU conditions) and \( h_{\text{R}} = 32{\text{ m}} \) (for TU conditions). The propagation conditions were of the NLOS type (κ = 0), while local scatterings around the transmitter occurred with varying intensity. Therefore, according to the suggestions resulting from the measurements [34], γ = 40 was assumed for the BU environment and γ = 120 for the TU environment. The number of clusters (L + 1 = 6) and the values of P l and τ l (0 ≤ l ≤ L), shown in Tables 2 and 3, were assumed on the basis of the measured PDS.
On the basis of the measurement procedure presented in [28], analysis of the results was carried out for a route with a length \( S = 100\lambda \cong 16{\text{ m}} \), where λ is the wavelength, which results from the frequency of the transmitted signal (\( f_{ 0} = 1800\,{\text{MHz}} \)). On this route, the measurement sections in the amount of hundred (M = 100) were designated. For these sections, we assumed that the received signal parameters have fixed values. In simulation studies, we also assumed that the number of paths in each cluster is K l = 10 (l = 0, 1, 2, …, L). The measurement results [28] are shown in Fig. 11, while for simulation by using DMCM, the exemplary PASs are illustrated in Fig. 12.
PASs—Results of measurements for a TU area (Aarhus) and a BU area (Stockholm) [28]
Example PASs—Results based on simulations by using DMCM for test scenario [28]
Figures 11 and 12 also present the Laplace model (LM) \( P\left( \phi \right) = P_{\text{LM}} \left( \phi \right) \) to facilitate the graphical comparison of measurement and simulation results. LM is defined by [28]
where \( \phi \in ( - 1 80^{ \circ } ; + 1 80^{ \circ } ],\sigma = 5. 5 8^{ \circ } \) for TU, and σ = 10.24∘ for BU [28]. It should be noted that, the selection criterion of σ value was minimization of the approximation error between LM and measurement data.
As can be seen from the above-mentioned figures, the use of DMCM produces PASs similar to the measurement results [28]. To assess the accuracy of the estimation of PAS, the rms angle spread of power, σ ϕ , is used
where \( \varPhi = {{\int\nolimits_{ - \xi }^{\xi } {\phi \, P\left( \phi \right)d\phi } }/{\int\nolimits_{ - \xi }^{\xi } {P\left( \phi \right)d\phi } }} \). Due to the limited range of angle variation in the empirical PASs [28], ξ = 30∘ is adopted.
On the basis of measurement results [28], authors obtained, \( \sigma_{{\phi {\text{ TU}}}} = 6.61^{ \circ } \) for a TU environment and \( \sigma_{{\phi {\text{ BU}}}} = 9.74^{ \circ } \) for a BU environment. In the case of simulations (results presented in Fig. 11), the values of the analysed parameter are as follows: \( \sigma_{{\phi {\text{ TU}}}} = 6.30^{ \circ } \) and \( \sigma_{{\varphi {\text{ BU}}}} = 9.48^{ \circ } \). The mean values of this parameter were obtained for a hundred simulation procedures, and these were \( \overline{{\sigma_{{\varphi {\text{ TU}}}} }} = 6.40^{ \circ } \pm 0.09^{ \circ } \) and \( \overline{{\sigma_{{\phi {\text{ BU}}}} }} = 9.52^{ \circ } \pm 0.14^{ \circ } \), respectively. The graphical representation of the averaged PASs is shown in Fig. 13.
Averaged PASs—Results based on simulations by using DMCM for test scenario [28]
Comparison of the results showed that for different environmental conditions, DMCM provides diverse PAS and gives results that are consistent with the measurement results obtained in real-world conditions. A complete verification of DMCM requires tests in a wide range of empirical data.
In order to access the possibility of DMCM the authors have developed a software implementation in MATLAB (see Appendix).
7 Conclusions
This paper presented the radio channel model, which structure consists of a geometric channel model and statistic models of the received signal parameters. This model was named the Doppler multi-elliptical channel model (DMCM) due to the possibility of mapping the effects of moving objects and the dispersive nature of the modelled channels. The input data for the model were the spatial location and motion parameters of objects (transmitter/receiver), the PDP, or PDS, which are closely related to the transmission properties of propagation environment. As a result, the developed model allowed us to obtain all the basic characteristics of the channel, including those related to the spatial position of the objects. In contrast to the previously presented models in the literature, DMCM provides integration of all basic phenomena, such as fluctuations and delay spread, as well as the phenomena that stem from the spatial nature in real channels. In the present study, this fact was shown using the example of selected propagation scenarios.
The main difficulty in the practical application of existing models is the problem of matching of their parameters to modelled scenarios. The PDP and PDS are characteristics that, in the measurement practice, are the basis for the assessment of the transmission properties of a channel. Therefore, DMCM ensures evaluation of the impact of the channel on the signal characteristics within a wide scope, including time domain (envelope vs. time), value (PDF, CDF, and the ACF of the envelope), frequency (PDS), and space (PAS). Accordingly, the developed model provides a good mapping of the transmission properties of the modelled propagation environment. This fact significantly distinguishes DMCM from most of the models previously presented in the literature.
In contrast to standard models, such as COST 207 or WINNER, DMCM also provided mapping of the impact of the spatial position and motion parameters of the objects on the channel characteristics that determines its originality. In COST 207 and WINNER models, it is not possible to test of each scenario, because the channel transmission characteristics (e.g. PDS) are precisely defined and they do not depend on Tx-Rx distance. In the empirical scenarios [28, 29], PDSs are significant difference in relation to PDSs of COST 207 and WINNER.
The use of the ellipsoid to 3D modeling and phase differences in the multi-antenna system to MIMO modeling will be the part of next extended work. Lastly, the simplicity of the practical implementation of DMCM, when compared with most of the models presented in the literature, is also worth mentioning.
References
Jakes, W. C., Jr. (1994). Microwave mobile communications (2nd ed.). Piscataway, NJ: Wiley-IEEE Press.
Parsons, J. D. (2000). The mobile radio propagation channel (2nd ed.). Chichester; New York: Wiley.
Rice, S. O. (1948). Statistical properties of a sine wave plus random noise. Bell System Technical Journal, 27(1), 109–157.
Suzuki, H. (1977). A statistical model for urban radio propagation. IEEE Transactions on Communications, 25(7), 673–680. doi:10.1109/TCOM.1977.1093888.
Hansen, F., & Meno, F. I. (1977). Mobile fading-Rayleigh and lognormal superimposed. IEEE Transactions on Vehicular Technology, 26(4), 332–335. doi:10.1109/T-VT.1977.23703.
Pätzold, M. (2011). Mobile radio channels (2nd ed.). Chichester; Hoboken, NJ: Wiley.
Simon, M. K., & Alouini, M.-S. (2004). Digital communication over fading channels (2nd ed.). Hoboken, NJ: Wiley-IEEE Press.
Vaughan, R., & Bach Andersen, J. (2003). Channels, propagation and antennas for mobile communications. London: Institution of Electrical Engineers.
Beckmann, P. (1967). Probability in communication engineering. New York: Harcourt, Brace and World.
Charash, U. (1979). Reception through Nakagami fading multipath channels with random delays. IEEE Transactions on Communications, 27(4), 657–670. doi:10.1109/TCOM.1979.1094444.
Yacoub, M. D. (2007). The α–μ distribution: A physical fading model for stacy distribution. IEEE Transactions on Vehicular Technology, 56(1), 27–34. doi:10.1109/TVT.2006.883753.
Yacoub, M. D. (2007). The κ–μ distribution and the η–μ distribution. IEEE Antennas and Propagation Magazine, 49(1), 68–81. doi:10.1109/MAP.2007.370983.
Stüber, G. L. (2011). Principles of mobile communication (3rd ed.). New York: Springer.
Olenko, A. Y., Wong, K. T., & Ng, E. H.-O. (2003). Analytically derived TOA–DOA statistics of uplink/downlink wireless multipaths arisen from scatterers on a hollow-disc around the mobile. IEEE Antennas and Wireless Propagation Letters, 2(1), 345–348. doi:10.1109/LAWP.2004.824174.
Petrus, P., Reed, J. H., & Rappaport, T. S. (2002). Geometrical-based statistical macrocell channel model for mobile environments. IEEE Transactions on Communications, 50(3), 495–502. doi:10.1109/26.990911.
Ertel, R. B., & Reed, J. H. (1999). Angle and time of arrival statistics for circular and elliptical scattering models. IEEE Journal on Selected Areas in Communications, 17(11), 1829–1840. doi:10.1109/49.806814.
Jiang, L., & Tan, S. Y. (2004). Simple geometrical-based AOA model for mobile communication systems. Electronics Letters, 40(19), 1203–1205. doi:10.1049/el:20045599.
Khan, N. M., Simsim, M. T., & Rapajic, P. B. (2008). A generalized model for the spatial characteristics of the cellular mobile channel. IEEE Transactions on Vehicular Technology, 57(1), 22–37. doi:10.1109/TVT.2007.904532.
Liberti, J. C., & Rappaport, T. S. (1999). Smart antennas for wireless communications: IS-95 and third generation CDMA applications. Upper Saddle River, NJ: Prentice Hall PTR.
Olenko, A. Y., Wong, K. T., & Abdulla, M. (2005). Analytically derived TOA–DOA distributions of uplink/downlink wireless-cellular multipaths arisen from scatterers with an inverted-parabolic spatial distribution around the mobile. IEEE Signal Processing Letters, 12(7), 516–519. doi:10.1109/LSP.2005.847859.
Zekavat, S. A., & Nassar, C. R. (2003). Power-azimuth-spectrum modeling for antenna array systems: A geometric-based approach. IEEE Transactions on Antennas and Propagation, 51(12), 3292–3294. doi:10.1109/TAP.2003.820973.
Janaswamy, R. (2002). Angle and time of arrival statistics for the Gaussian scatter density model. IEEE Transactions on Wireless Communications, 1(3), 488–497. doi:10.1109/TWC.2002.800547.
Lötter, M. P., & Van Rooyen, P. G. W. (1999). Modeling spatial aspects of cellular CDMA/SDMA systems. IEEE Communications Letters, 3(5), 128–131. doi:10.1109/4234.766845.
Le, K. N. (2009). On angle-of-arrival and time-of-arrival statistics of geometric scattering channels. IEEE Transactions on Vehicular Technology, 58(8), 4257–4264. doi:10.1109/TVT.2009.2023255.
Jiang, L., & Tan, S. Y. (2007). Geometrically based statistical channel models for outdoor and indoor propagation environments. IEEE Transactions on Vehicular Technology, 56(6), 3587–3593. doi:10.1109/TVT.2007.901055.
Parsons, J. D., & Bajwa, A. S. (1982). Wideband characterisation of fading mobile radio channels. Communications, Radar and Signal Processing, IEE Proceedings F, 129(2), 95–101. doi:10.1049/ip-f-1:19820016.
Rafa, J., & Ziółkowski, C. (2008). Influence of transmitter motion on received signal parameters—Analysis of the Doppler effect. Wave Motion, 45(3), 178–190. doi:10.1016/j.wavemoti.2007.05.003.
Pedersen, K. I., Mogensen, P. E., & Fleury, B. H. (2000). A stochastic model of the temporal and azimuthal dispersion seen at the base station in outdoor propagation environments. IEEE Transactions on Vehicular Technology, 49(2), 437–447. doi:10.1109/25.832975.
Felhauer, T., Baier, P. W., König, W., & Mohr, W. (1994). Wideband characterisation of fading outdoor radio channels at 1800 MHz to support mobile radio system design. Wireless Personal Communications, 1(2), 137–149. doi:10.1007/BF01098691.
Seidel, S. Y., Rappaport, T. S., Jain, S., Lord, M. L., & Singh, R. (1991). Path loss, scattering and multipath delay statistics in four European cities for digital cellular and microcellular radiotelephone. IEEE Transactions on Vehicular Technology, 40(4), 721–730. doi:10.1109/25.108383.
COST 207 Working Group on Propagation. (WG 1). (1986). Proposal on channel transfer functions to be used in GSM tests late 1986 (No. COST 207 TD (86) 51 Rev. 3).
IST-WINNER II. (2007). WINNER II channel models (No. IST-WINNER II Tech. Rep. Deliverable 1.1.2 v.1.2.). Retrieved from http://www.ist-winner.org/WINNER2-Deliverables/D1.1.2.zip.
Papoulis, A., & Pillai, S. U. (2002). Probability, random variables, and stochastic processes (4th ed.). Boston: McGraw-Hill.
Abdi, A., Barger, J. A., & Kaveh, M. (2002). A parametric model for the distribution of the angle of arrival and the associated correlation function and power spectrum at the mobile station. IEEE Transactions on Vehicular Technology, 51(3), 425–434. doi:10.1109/TVT.2002.1002493.
Lee, W. C. Y. (1985). Estimate of local average power of a mobile radio signal. IEEE Transactions on Vehicular Technology, 34(1), 22–27. doi:10.1109/T-VT.1985.24030.
Jakes, W. C., Jr, & Reudink, D. O. (1967). Comparison of mobile radio transmission at UHF and X band. IEEE Transactions on Vehicular Technology, 16(1), 10–14. doi:10.1109/T-VT.1967.23375.
Tao, F., & Field, T. R. (2008). Statistical analysis of mobile radio reception: an extension of Clarke’s model. IEEE Transactions on Communications, 56(12), 2007–2012. doi:10.1109/TCOMM.2008.060596.
Ziółkowski, C., & Kelner, J. M. (2014). DMCM ver. 2.0. Doppler Multi-elliptical Channel Model. Retrieved from http://www.dmcm.org.pl/.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
A test implementation is available in the form of a p-file (pseudo-code) on the website [38]. For the selected input data, DMCM_all procedure makes it possible to obtain a matrix of the received signal parameters (\( r_{lk} ,\varphi_{lk} ,f_{Dlk} ,\alpha_{lk} \)), the signal (x s (t)), and the characteristics (ACF, PSD, and PAS).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Ziółkowski, C., Kelner, J.M. Geometry-Based Statistical Model for the Temporal, Spectral, and Spatial Characteristics of the Land Mobile Channel. Wireless Pers Commun 83, 631–652 (2015). https://doi.org/10.1007/s11277-015-2413-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-015-2413-3