Bit Error Rate of SSTS for Downlink Distributed Antenna Systems in Multicell Environment

Abstract

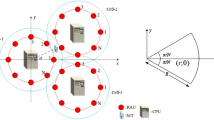
Based on maximum desired signal criterion, a novel single selection transmission scheme (SSTS) is proposed. In this case, the bit error rate (BER) of downlink distributed antenna systems in multicell environment is investigated. In particular, non-central limit theorem is adopted for SSTS to embody the effect of short-term fading on interference, where the variance of interference plus noise is considered as random variable with changeable variance influenced by the short-term fading. It is assumed that the channels suffer from independent identical Rayleigh fading together with propagation pathloss, and the closed-form expression of BER is derived. Extensive simulations are carried out to validate the theoretical derivation.

Appendix 1: Gauss–Hermite Quadrature

The Gauss–Hermite formula is expressed as [22]:

$$\begin{aligned} \int _{ - \infty }^{ + \infty } {\exp \left( { - {x^2}} \right) f\left( x \right) dx} = \sum \limits _{i = 1}^n {{H_i}f\left( {{x_i}} \right) } + {R_n} \simeq \sum \limits _{i = 1}^n {{H_i}f\left( {{x_i}} \right) } \end{aligned}$$

(26)

where $n$ is the order of Hermite polynomial (the number of sample points to use for the approximation). The $x_i$ are the roots of the Hermite polynomial ${H_n}\left( x \right) \;\left( {i = 1, \ldots ,n} \right)$ and the associated weights $H_i$ are given as:

$$\begin{aligned} {H_i} = \frac{{{2^{n - 1}}n!\sqrt{\pi }}}{{{n^2}{{\left[ {{H_{n - 1}}\left( {{x_i}} \right) } \right] }^2}}} \end{aligned}$$

(27)

The Hermite polynomial ${H_n}\left( x \right)$ is written as [23]:

$$\begin{aligned} {H_n}\left( x \right)&= {{\left( { - 1} \right) }^n}\exp \left( {{x^2}} \right) \frac{{{d^n}}}{{d{x^n}}}\left( {\exp \left( { - {x^2}} \right) } \right) \;\;\;\;\; or \nonumber \\ {H_n}\left( x \right)&= {2^n}{x^n} - 2^{n - 1}{n \atopwithdelims ()2}{x^{n - 1}} \nonumber \\&+ \,\,{2^{n - 2}} \cdot 1 \cdot 3 \cdot {n \atopwithdelims ()4} {x^{n-4}} - {2^{n - 3}} \cdot 1 \cdot 3 \cdot 5 \cdot {n \atopwithdelims ()6} {x^{n-6}} + \cdots \nonumber \\ {H_0}\left( x \right)&= 1 \end{aligned}$$

(28)

The remainder in Eq. (25) is given as:

$$\begin{aligned} {R_n} = \frac{{n!\sqrt{\pi }}}{{{2^n}\left( {2n} \right) !}}{f^{\left( {2n} \right) }}\left( \xi \right) \;\;\;\;\left( { - \infty < \xi < \infty } \right) \end{aligned}$$

(29)

where $\xi$ is arbitrary selected and ${f^{\left( n \right) }}\left( x \right)$ is the $n$-th derivative of $f\left( x \right)$.

The precision of Gauss–Hermite approximation is dominated by $n$. If the number of sample points $\left( n \right)$ is not enough, the approximate curve and the exact curve are not in excellent agreement. On the contrary, the larger of $n$, the more accurate of the approximation we can get.