Iterative Overlap QRM-ML Block Detection for Single-Carrier MIMO Transmission Without CP Insertion

Abstract

QR decomposition and M-algorithm based near maximum likelihood block detection (QRM-MLBD) significantly improves the single-carrier (SC) multiple-input multiple-output (SC-MIMO) transmission performance in a frequency-selective fading channel. In the conventional QRM-MLBD, the cyclic prefix (CP) is inserted in order to avoid the inter-block interference (IBI). However, CP insertion reduces the transmission efficiency. In this paper, an iterative overlap QRM-MLBD is proposed for SC-MIMO transmission with no CP insertion. It is confirmed by computer simulation that the iterative overlap QRM-MLBD with no CP insertion provides improved throughput performance while reducing the computational complexity over the conventional QRM-MLBD with CP insertion.

1 Introduction

In the next generation mobile communication systems, broadband data services are demanded. Multiple-input multiple-output (MIMO) spatial multiplexing [1] provides broadband data transmissions without increasing the signal bandwidth. For uplink (mobile terminal to base-station) application, single-carrier (SC) transmission is suitable because of its lower peak-to-average power ratio (PAPR) property [2, 3] compared with multi-carrier transmission, e.g., orthogonal frequency division multiplexing (OFDM) [4]. Thus, SC-MIMO has been adopted for the uplink transmission in 3rd generation partnership project long term evolution-advanced (3GPP LTE-A) systems [5].

For broadband signal transmission, wireless channel is severely frequency-selective [6]. The broadband SC-MIMO spatial multiplexing suffers from inter-symbol interference (ISI) arising from the severe frequency-selectivity of the channel. The use of the cyclic prefix (CP) and frequency-domain block detection such as a computational efficient minimum mean square error (MMSE) based linear detection [7] can improve the transmission performance of SC-MIMO spatial multiplexing. However, a big performance gap from the maximum likelihood (ML) performance still exists due to the presence of residual ISI and inter-antenna interference (IAI). Recently, QR decomposition and M-algorithm based near-maximum likelihood block detection (QRM-MLBD) was proposed [8, 9] for broadband SC-MIMO spatial multiplexing. QRM-MLBD significantly improves the transmission performance of SC-MIMO spatial multiplexing in a frequency-selective fading channel while significantly reducing the computational complexity compared with ML detection.

The conventional block detection schemes, such as MMSE based linear detection and QRM-MLBD, require the insertion of CP to avoid the inter-block interference (IBI). However, CP insertion reduces the transmission efficiency. As a linear detection, overlap frequency-domain linear detection was proposed [10–12] in which the received symbol stream is divided into a sequence of blocks of $X$ symbols each and then, frequency-domain block detection is applied to an extended block of $N_{c}$ symbols centering the $X$-symbol block of interest $(X\le N_{c})$. Note that $N_{c}$-symbol block is first transformed by the discrete Fourier transform (DFT) into the frequency-domain signal. Knowing that the residual IBI is significant near both ends of $N_{c}$-symbol block after MMSE based linear detection, only $X$ symbols are picked up in order to avoid the residual IBI. However, a big performance gap from the ML performance is observed due to insufficient suppression of interferences, i.e., IAI, ISI, and also IBI.

In [13, 14], we presented the SC transmission using time-domain iterative overlap QRM-MLBD with no CP insertion for single-input single-output (SISO) systems. In overlap QRM-MLBD, the concept of overlap processing is applied to QRM-MLBD, in which the received symbol stream is divided into a sequence of blocks of $X$ symbols each and then, QRM-MLBD is applied to an extended block of $N_{c}+L-1$ symbols to detect an $N_{c}$-symbol block including the $X$-symbol block of interest at the beginning, where $L$ denotes the channel length in symbols (in this paper, the channel is assumed to be composed of symbol-spaced $L$ propagation paths). The residual IBI is significant near the end of $N_{c}$-symbol block after QRM-MLBD. Based on the above observation, only $X$ symbols are picked up in order to avoid the residual IBI. To improve the IBI suppression, iterative processing and IBI cancellation are also introduced. Note that the proposed iterative overlap QRM-MLBD is implemented in the time-domain (no DFT is used in block detection). This is because time-domain overlap QRM-MLBD is equivalent to the frequency-domain overlap QRM-MLBD [13] and time-domain processing has an advantage in terms of the computational complexity.

In this paper, we extend the previously proposed iterative overlap QRM-MLBD to SC-MIMO spatial multiplexing with no CP insertion. To extend our previously proposed algorithm to the MIMO systems, we introduce an appropriate modification of the received signal vector for SC-MIMO spatial multiplexing. It is confirmed by computer simulation that the iterative overlap QRM-MLBD with no CP insertion can achieve significant performance improvement while reducing the computational complexity compared to the conventional QRM-MLBD with CP insertion.

The rest of the paper is organized as follows. Section 2 describes the iterative overlap QRM-MLBD for SC-MIMO spatial multiplexing with no CP insertion. Simulation results are presented in Sect. 3. The achievable throughput performance with the iterative overlap QRM-MLBD is compared with the conventional QRM-MLBD with CP insertion and the computational complexity of the iterative overlap QRM-MLBD is discussed as well. Finally, we conclude the paper in Sect. 4.

2 Iterative Overlap QRM-MLBD

2.1 Transmission System Model

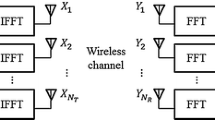
Figure 1 illustrates the transmitter/receiver structure of SC-MIMO spatial multiplexing using the iterative overlap QRM-MLBD, where the numbers of transmit antennas and receive antennas are denoted by $N_{t}$ and $N_{r}$, respectively. At the transmitter, the information bit sequence is transformed into a data-modulated symbol sequence and then, serial-to-parallel (S/P) converted to $N_{t}$ parallel symbol sequences and each symbol sequence is transmitted from a different antenna.

Fig. 1

Transmission system model. a Transmitter. b Receiver

The transmitted symbol sequence of each transmit antenna propagates through different channel and received by $N_{r}$ receive antennas at the receiver. The received symbol sequence on each receive antenna is divided into a sequence of blocks of $X$ symbols each. To detect an $N_{c}$-symbol block including the $X$-symbol block of interest at the beginning, block signal processing is applied to an extended block of $N_{c}+L-1$ symbols (referred to as observation window).

Iterative processing is applied to reduce the residual IBI. In the $i$th iteration stage, the replica of IBI from the previous block is generated by using the $i$th stage decision of the previous block. The replica of IBI from the next block is generated by the $(i-1)$th stage decision of the next block. The IBIs are removed by subtracting their replicas from the received symbol sequence of interest over the observation window before applying QRM-MLBD. The received symbol sequence over the observation window at each receive antenna after IBI suppression is represented by a column vector of $N_{c}+L-1$ elements. $N_{r}$ received symbol vectors are stacked to form a stacked received symbol vector. Then, by appropriately modifying the stacked received symbol vector, QRM-MLBD is applied to detect $N_{t}$ transmitted blocks of $N_{c}$ symbols each. After QRM-MLBD, the first $X$-symbol block is picked up for each transmit antenna from each detected block of $N_{c}$ symbols.

To detect the next $X$-symbol block, the observation window is shifted by $X$ symbols as shown in Fig. 2. By repeating this process, the continuously transmitted symbol sequence from each transmit antenna is detected. The above overlap QRM-MLBD processing is repeated $I$ times ($I=0$ represents the initial iteration stage) to suppress the residual IBI sufficiently.

Fig. 2

Iterative overlap QRM-MLBD

2.2 Received Signal Representation

A frequency-selective fading channel is assumed to be composed of symbol-spaced $L$ distinct propagation paths with different time delays. The channel impulse response between the $n_{t}$th transmit antenna and the $n_{r}$th receive antenna $h_{n_r ,n_t } (\uptau )$ is expressed as

$$\begin{aligned} h_{n_r ,n_t } (\uptau )=\sum _{l=0}^{L-1} {h_{n_r ,n_t ,l} \delta } (\uptau -\tau _{n_r ,n_t ,l}), \end{aligned}$$

(1)

where $h_{n_r ,n_t ,l}$ and $\uptau _{n_r ,n_t ,l}$ are respectively the complex-valued path gain with $E[|h_{n_r ,n_t ,l} |^{2}]{=}1$ and the time delay of the $l$th path between the $n_{t}$th transmit antenna and the $n_{r}$th receive antenna. The received $N_{c}+L-1$-symbol sequence, $\mathbf{y}_{n_r } =[y_{n_r } (0),\ldots ,y_{n_r } (t),\ldots ,y_{n_r } (N_c +L-2)]^{T}$ with $(.)^{T}$ denoting the transpose operation, over the observation window on the $n_{r}$th receive antenna can be expressed using the matrix form as

$$\begin{aligned} \mathbf{y}_{n_r }&= \sqrt{\frac{2E_s}{T_s N_t}}\sum _{n_t =0}^{N_t-1} {\mathbf{h}_{n_r,n_t} \mathbf{d}_{n_t}} +\sqrt{\frac{2E_s }{T_s N_t}}\sum _{n_t =0}^{N_t -1} {\mathbf{h}_{n_r ,n_t,-1}\mathbf{d}_{n_t,-1}}\nonumber \\&\quad +\,\sqrt{\frac{2E_s}{T_s N_t}}\sum _{n_t =0}^{N_t-1}{\mathbf{h}_{n_r ,n_t,+1}\mathbf{d}_{n_t,+1}}+\mathbf{n}_{n_r}, \end{aligned}$$

(2)

where $E_{s}$ and $T_{s}$ are respectively the symbol energy and duration. $\mathbf{d}_{n_t}=[d_{n_t}(0),\ldots ,d_{n_t} (t),\ldots , d_{n_t} (N_c -1)]^{T}$ represents the transmit symbol vector of interest from the $n_{t}$th transmit antenna. $\mathbf{d}_{n_t, -1(+1)}=[d_{n_t ,-1(+1)}(0),\ldots ,d_{n_t,-1(+1)} (t),\ldots ,d_{n_t,-1(+1)}(N_c -1)]^{T}$ represents the previous (next) transmit symbol vector. The first term of (2) denotes the desired signal and the second and third terms denote the IBI from the previous and the next blocks, respectively. $\mathbf{n}_{n_r } =[n_{n_r }(0),\ldots ,n_{n_r }(t),\ldots ,n_{n_r }(N_c +L-2)]^{T}$ is the zero-mean additive white Gaussian noise (AWGN) vector with the one-sided power spectrum density $N_{0}$. $\mathbf{h}_{n_r ,n_t} ,\mathbf{h}_{n_r ,n_t ,-1}$, and $\mathbf{h}_{n_r ,n_t ,+1}$ are respectively $(N_{c}+L-1)\times N_{c}$ channel impulse response matrixes between the $n_{t}$th transmit antenna and the $n_{r}$th receive antenna, given as

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{h}_{n_r ,n_t} \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {h_{n_r ,n_t ,0}}&{} &{} &{} \mathbf{0} \\ \vdots &{} \ddots &{} &{} \\ {h_{n_r ,n_t ,L-1}}&{} &{}\ddots &{} \\ &{} \ddots &{} &{} {h_{n_r ,n_t ,0}} \\ &{} &{} \ddots &{} \vdots \\ \mathbf{0}&{} &{} &{}{h_{n_r ,n_t ,L-1}} \\ \end{array} }} \right] \\ \mathbf{h}_{n_r ,n_t ,-1} \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {h_{n_r ,n_t ,L-1} }&{} \cdots &{} {h_{n_r ,n_t ,1}} \\ &{} \ddots &{} \vdots \\ &{} &{} {h_{n_r ,n_t ,L-1}} \\ \mathbf{0}&{} &{} \\ \end{array}}} \right] ,\mathbf{h}_{n_r ,n_t ,+1} \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} &{} &{} \mathbf{0}&{} \\ &{} &{} &{} \\ {h_{n_r ,n_t ,0} }&{} &{} &{} \\ \vdots &{} \ddots &{} &{} \\ {h_{n_r ,n_t ,L-2} }&{} \cdots &{} {h_{n_r ,n_t ,0} }&{} \\ \end{array} }} \right] \\ \end{array}} \right. .\nonumber \\ \end{aligned}$$

(3)

2.3 Iterative Overlap QRM-MLBD

2.3.1 Stacked Received Symbol Vector

In the $i$th iteration stage, the IBI replica from the previous block is generated by using the decision of ${\hat{{\mathbf{d}}}}_{n_t ,-1}^{(i)} =[\hat{{d}}_{n_t ,-1}^{(i)} (0),\ldots ,\hat{{d}}_{n_t ,-1}^{(i)} (t),\ldots ,\hat{{d}}_{n_t ,-1}^{(i)} (N_c -1)]^{T}, n_{t}=0\sim N_{t}-1$, of the previous block. When $i\ge 1$, the IBI replica from the next block is also generated by using the decision of ${\hat{{\mathbf{d}}}}_{n_t ,+1}^{(i-1)} =[\hat{{d}}_{n_t ,+1}^{(i-1)} (0),\ldots ,\hat{{d}}_{n_t ,+1}^{(i-1)} (t),\ldots ,\hat{{d}}_{n_t,+1}^{(i-1)} (N_c -1)]^{T},n_{t}=0\sim N_{t}-1$, of the next block. The IBI cancellation is performed by subtracting the IBI replicas from the received signal as

$$\begin{aligned} \tilde{\mathbf{y}}_{n_r }^{(i)} =\mathbf{y}_{n_r } -\left( {\sqrt{\frac{2E_s }{T_s N_t }}\sum _{n=0}^{N_t -1} {\mathbf{h}_{n_r ,n_t ,-1} {\hat{\mathbf{d}}}_{n_t ,-1}^{(i)} } +\sqrt{\frac{2E_s }{T_s N_t }}\sum _{n=0}^{N_t -1} {\mathbf{h}_{n_r ,n_t ,+1} {\hat{\mathbf{d}}}}_{n_t,+1}^{(i-1)}} \right) . \end{aligned}$$

(4)

The received symbol vector after the IBI cancellation at each receive antenna is stacked to form an $N_{r}(N_{c}+L-1)\times 1$ stacked received symbol vector ${\tilde{\mathbf{Y}}}^{(i)}=[{\begin{array}{lll} {\{{\tilde{\mathbf{y}}}_0^{(i)} \}^{T}}&{} \cdots &{} {\{{\tilde{\mathbf{y}}}_{N_r -1}^{(i)} \}^{T}} \\ \end{array}}]^{T}$ as

$$\begin{aligned} {\tilde{\mathbf{Y}}}^{(i)}&= [{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\{\tilde{\mathbf{y}}_0^{(i)}\}^{T}}&{} \cdots &{} {\{\tilde{\mathbf{y}}_{N_r -1}^{(i)} \}^{T}} \\ \end{array} }]^{T} \nonumber \\&= \sqrt{\frac{2E_s }{T_s N_t}}\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0} }&{} \cdots &{} {\mathbf{h}_{0,N_t -1} } \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0}}&{} \cdots &{}{\mathbf{h}_{N_r -1,N_t -1} } \\ \end{array}}} \right] \left[ {{\begin{array}{c} {\mathbf{d}_0} \\ \vdots \\ {\mathbf{d}_{N_t -1}} \\ \end{array}}} \right] +\left[ {{\begin{array}{c} {\mathbf{n}_0} \\ \vdots \\ {\mathbf{n}_{N_r -1 }} \\ \end{array} }}\right] \nonumber \\&\quad +\,\sqrt{\frac{2E_s }{T_s N_t }}\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0,-1} }&{} \cdots &{} {\mathbf{h}_{0,N_t -1,-1}} \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0,-1}}&{} \cdots &{} {\mathbf{h}_{N_r -1,N_t -1,-1}} \\ \end{array}}} \right] \left[ {{\begin{array}{c} {\mathbf{d}_{0,-1}-\hat{\mathbf{d}}_{0,-1}^{(i)} } \\ \vdots \\ {\mathbf{d}_{N_t -1,-1} -\hat{\mathbf{d}}_{N_t -1,-1}^{(i)}} \\ \end{array} }} \right] \nonumber \\&\quad +\,\sqrt{\frac{2E_s }{T_s N_t}}\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0,+1} }&{} \cdots &{}{\mathbf{h}_{0,N_t -1,+1}} \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0,+1} }&{} \cdots &{} {\mathbf{h}_{N_r -1,N_t -1,+1}} \\ \end{array}}} \right] \left[ {{\begin{array}{c} {\mathbf{d}_{0,+1} - \hat{\mathbf{d}}_{0,+1}^{(i-1)}} \\ \vdots \\ {\mathbf{d}_{N_t -1,+1} -\hat{\mathbf{d}}_{N_t -1,+1}^{(i-1)}} \\ \end{array} }} \right] \nonumber \\&= \sqrt{\frac{2E_s }{T_s N_t }}\mathbf{HD}+\sqrt{\frac{2E_s }{T_s N_t }} \mathbf{H}_{-1} \left( \mathbf{D}_{-1} -\hat{\mathbf{D}}_{-1}^{(i)}\right) +\sqrt{\frac{2E_s }{T_s N_t }}\mathbf{H}_{+1} \left( \mathbf{D}_{+1} -\hat{\mathbf{D}}_{+1}^{(i-1)}\right) +\mathbf{N},\qquad \end{aligned}$$

(5)

where $\mathbf{N}=[{\begin{array}{l@{\quad }l@{\quad }l} {\{\mathbf{n}_0 \}^{T}}&{} \cdots &{} {\{\mathbf{n}_{N_r -1} \}^{T}} \\ \end{array} }]^{T}$ is the $N_{r}(N_{c}+ L-1)\times 1$ stacked noise vector. $\mathbf{D}=[{\begin{array}{c@{\quad }c@{\quad }c} {\{\mathbf{d}_0 \}^{T}}&{} \cdots &{} {\{\mathbf{d}_{N_t -1} \}^{T}} \\ \end{array} }]^{T},\mathbf{D}_{-1} =[{\begin{array}{c@{\quad }c@{\quad }c} {\{\mathbf{d}_{0,-1} \}^{T}}&{} \cdots &{} {\{\mathbf{d}_{N_t -1,-1} \}^{T}} \\ \end{array} }]^{T}$, and $\mathbf{D}_{+1} =[{\begin{array}{c@{\quad }c@{\quad }c} {\{\mathbf{d}_{0,+1} \}^{T}}&{} \cdots &{} {\{\mathbf{d}_{N_t -1,+1} \}^{T}} \\ \end{array} }]^{T}$ are the $N_{t}N_{c}\times 1$ stacked transmit symbol vectors. H,H $_{-1}$, and H $_{+1}$ are equivalent channel matrixes of size $N_{r}(N_{c}+L-1)\times N_{t}N_{c}$, which represent space and time-domain channel, given by

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{H}\!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0} }&{} \cdots &{} {\mathbf{h}_{0,N_t -1} } \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0} }&{} \cdots &{} {\mathbf{h}_{N_r -1,N_t -1} } \\ \end{array} }} \right] \\ \mathbf{H}_{-1} \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0,-1} }&{} \cdots &{} {\mathbf{h}_{0,N_t -1,-1} } \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0,-1} }&{} \cdots &{} {\mathbf{h}_{N_r -1,N_t -1,-1} } \\ \end{array} }} \right] ,\hbox { }\mathbf{H}_{+1} \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{h}_{0,0,+1} }&{} \cdots &{} {\mathbf{h}_{0,N_t -1,+1} } \\ \vdots &{} \ddots &{} \vdots \\ {\mathbf{h}_{N_r -1,0,+1} }&{} \cdots &{} {\mathbf{h}_{N_r -1,N_t -1,+1} } \\ \end{array} }} \right] \\ \end{array}} \right. .\nonumber \\ \end{aligned}$$

(6)

The second and the third terms of (5) are the residual IBIs from the previous and the next blocks, respectively.

2.3.2 Modification of the Stacked Received Symbol Vector

Overlap QRM-MLBD for SISO systems [13, 14] utilizes the property that the IBI from the next block, which cannot be removed in the initial iteration stage, exists only on the elements near the bottom of the received symbol vector. QRM-MLBD is applied to the received symbol vector and then, the residual IBI is significant near the end of $N_{c}$-symbol block after QRM-MLBD. Therefore, symbol error rate near the beginning of the block is lower while symbol error rate near the end of the block is higher. Based on the above observation, overlap QRM-MLBD can effectively suppress the IBI by picking up only the reliable first $X$-symbol block from the $N_{c}$-symbol block.

However, in (5), the IBI from the next block exists on the elements near the bottom of received symbol vector at each receive antenna. Therefore, if QRM-MLBD is applied to (5) directly, the effect of IBI spreads over the all symbols in the entire block. To extend the previously proposed overlap QRM-MLBD to the MIMO systems, we modify the stacked received symbol vector as

$$\begin{aligned} {\tilde{\mathbf{Y}}}^{\prime (i)}=[\{\tilde{ \mathbf{Y}}^{(i)}{(0)\}^{T}},\ldots ,\{\tilde{\mathbf{Y}}^{(i)}{(t)\}^{T}},\ldots ,{\{\tilde{\mathbf{Y}}^{(i)}(N_c -L-2)\}^{T}]^{T}}, \end{aligned}$$

(7)

where ${\tilde{\mathbf{Y}}}^{(i)}(t)=[{\tilde{\mathbf{Y}}}_0^{(i)} (t),\ldots ,{\tilde{\mathbf{Y}}}_{N_r -1}^{(i)} (t)]^{T}$ denotes the $t\hbox {th}$ $N_{r}\times$ 1 size received symbol vector after IBI cancellation. After the above modification, the equivalent channel matrixes corresponding to the IBIs from the previous and the next blocks are permutated as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\overline{\mathbf{H}}^{\prime }_{-1} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} &{} {\mathbf{{H}}^{\prime }_{0,L-1} }&{} \cdots &{} {\mathbf{{H}}^{\prime }_{0,1} } \\ &{} &{} \ddots &{} \vdots \\ &{} &{} &{} {\mathbf{{H}}^{\prime }_{0,L-1} } \\ &{} &{} &{} \\ &{} \mathbf{0}&{} &{} \\ &{} &{} &{} \\ \end{array} }{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} &{} {\mathbf{{H}}^{\prime }_{N_{t} -1,L-1} }&{} \cdots &{} {\mathbf{{H}}^{\prime }_{N_t -1,1} } \\ &{} &{} \ddots &{} \vdots \\ &{} &{} &{} {\mathbf{{H}}^{\prime }_{N_t -1,L-1} } \\ &{} &{} &{} \\ &{} \mathbf{0}&{} &{} \\ &{} &{} &{} \\ \end{array} }} \right] } \\ {{{\overline{\mathbf{H}}}}^{\prime }_{+1} = \left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} &{} &{} &{} \\ &{} &{} \mathbf{0}&{} \\ &{} &{} &{} \\ {\mathbf{{H}}^{\prime }_{0,1} }&{} &{} &{} \\ \vdots &{} \ddots &{} &{} \\ {\mathbf{{H}}^{\prime }_{0,L-2} }&{} \cdots &{} {\mathbf{{H}}^{\prime }_{0,0} }&{} \\ \end{array} }{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} &{} &{} &{} \\ &{} &{} \mathbf{0}&{} \\ &{} &{} &{} \\ {\mathbf{{H}}^{\prime }_{N_t -1,0} }&{} &{} &{} \\ \vdots &{} \ddots &{} &{} \\ {\mathbf{{H}}^{\prime }_{N_t -1,L-2} }&{} \cdots &{} {\mathbf{{H}}^{\prime }_{N_t -1,0} }&{} \\ \end{array} }} \right] } \\ \end{array} }} \right. , \end{aligned}$$

(8)

where $\mathbf{{H}^{\prime }}_{n_t ,l} =[h_{0,n_t ,l} \ldots ,h_{N_r -1,n_t ,l} ]^{T}$. It can be seen from (7) and (8) that the IBI from the next block exists only in the elements near the bottom of the modified stacked received symbol vector.

In QRM-MLBD, M-algorithm [15] is performed starting from the last symbol in the stacked transmit symbol vector. Since overlap QRM-MLBD outputs only $X$-symbol block for each transmit antenna which suffers less of the IBI from the next symbol block, the $N_{t}N_{c}$ symbols in the stacked transmit symbol vector D is changed as

$$\begin{aligned} \mathbf{{D}^\prime }=[\mathbf{D}^{T}(N_c -1),\ldots , \mathbf{D}^{T}(t),\ldots ,\mathbf{D}^{T}(0)]^{T}, \end{aligned}$$

(9)

where $\mathbf{D}(t)=[d_{N_t -1} (t),\ldots ,d_0 (t)]^{T}$ denotes the $t$th $N_{t}\times$1 size transmit symbol vector. By the above modification of the stacked received symbol vector and ordering of the stacked transmit symbol vector, the equivalent channel matrix for the desired signal component H is given as

(10)

where

$$\begin{aligned} \mathbf{{H}^{{\prime }{\prime }}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {h_{0,N_t -1,l} }&{} \cdots &{} {h_{0,0,l} } \\ \vdots &{} \ddots &{} \vdots \\ {h_{N_r -1,N_t -1,l} }&{} \cdots &{} {h_{N_r -1,0,l} } \\ \end{array} }} \right] . \end{aligned}$$

(11)

It can be seen from (7), (10), and (11) that the modified stacked received symbol vector is similar to the SISO case [14] as shown in Fig. 3. Therefore, the previously proposed overlap QRM-MLBD can be applied in a similar way to the MIMO system.

2.3.3 QRM-MLBD

QR decomposition is applied to the equivalent channel matrix ${{\overline{\mathbf{H}}}^{{\prime }{\prime }}}$ to obtain ${{\overline{\mathbf{H}}}^{{\prime }{\prime }}}=\mathbf{QR}$, where Q is an $N_{r}(N_{c}+L-1)\times N_{t}N_{c}$ unitary matrix and R is an $N_{t}N_{c}\times N_{t}N_{c}$ upper triangular matrix. Since the equivalent channel matrix for the desired signal component ${{\overline{\mathbf{H}}}^{{\prime }{\prime }}}$ is shown in (10), the unitary matrix Q and the upper triangular matrix R obtained by QR decomposition of ${{\overline{\mathbf{H}}}^{{\prime }{\prime }}}$ are represented as

(12)

The transformed received signal vector ${\hat{\mathbf{Y}}}^{(i)}$ is obtained as

$$\begin{aligned} {\hat{\mathbf{Y}}}^{(i)}&= \mathbf{Q}^{H}{{\tilde{\mathbf{Y}}}}^{{\prime }(i)} =\sqrt{\frac{2E_s }{T_s N_t }}\mathbf{R{D}^{\prime }}+\sqrt{\frac{2E_s }{T_s N_t }}{\hat{\mathbf{H}}}_{-1} \left( \mathbf{D}_{-1} -{\hat{\mathbf{D}}}_{-1}^{(i)}\right) \nonumber \\&+\sqrt{\frac{2E_s }{T_s N_t }}{\hat{\mathbf{H}}}_{+1} \Big (\mathbf{D}_{+1}\quad -{\hat{\mathbf{D}}}_{+1}^{(i-1)}\Big )+{\hat{\mathbf{N}}}, \end{aligned}$$

(13)

where ${\hat{\mathbf{H}}}_{-1} =\mathbf{Q}^{H}{{\overline{\mathbf{H}}}^{\prime }}_{-1} ,\; {\hat{\mathbf{H}}}_{+1} =\mathbf{Q}^{H}{{\bar{\mathbf{H}}}^{\prime }}_{+1},\; { \hat{\mathbf{N}}}=\mathbf{Q}^{H}\mathbf{N}$, and $(.)^{H}$ denotes the Hermitian transpose operation.

Fig. 3

Modified received signal vector $(N_{t}=N_{r}=2)$

From (13), the ML solution is to select the path with the minimum Euclidean distance in a $N_{t}N_{c}$-stages tree diagram. This can be realized by M-algorithm. At each stage, the best $M$ surviving paths selected from all the paths are passed to the next stage. The squared Euclidean distance is used for branch metric calculation. Data demodulation is carried out by tracing back the path having the smallest path metric at the last stage. In this paper, the stopping criterion [14] can be applied similarly to the SISO case to stop the tree search at an earlier stage to reduce the detection complexity. It can be seen from (12) and (13) that the branch metric beyond the $(N_{t}L+n)$th stage does not affect the detection of the $\left\lfloor {n/N_t } \right\rfloor$th data symbol transmitted from the ($n$ mod $N_{t})$th transmit antenna, where $\left\lfloor x \right\rfloor$ represents the largest integer smaller than or equal to $x$. Therefore, the tree search using M-algorithm can be stopped at the $(N_{t}(X+L)$-1)th stage in order to output an $X$-symbol block for each transmit antenna.

2.3.4 IBI power distribution

Without CP insertion, the previous and the next blocks produce IBI. In the initial iteration stage $(i=0)$, IBI from the previous block can be suppressed by using the decision of the previous block as (5). However, IBI from the next block cannot be removed. Here, we consider the distribution of IBI from next block after multiplying $\mathbf{Q}^{H}$ [third term of (13)]. It can be seen from (12) that since $\mathbf{Q}^{H}$ is an unitary matrix, the absolute value of each element of $\mathbf{Q}^{H}$ is larger in upper row vector. Therefore, the absolute value of each element of ${\hat{\mathbf{H}}}_{+1} =\mathbf{Q}^{H}{{\overline{\mathbf{H}}}^{\prime }}_{+1}$ of (13) is larger in an upper row vector and is smaller in a lower row vector. As a result, the IBI power from the next block is more significant at an element closer to the beginning of the transformed signal vector while the IBI power from the next block is less significant at an element near the end of the transformed signal vector. Hence, in the M-algorithm, the probability of erroneously removing the correct path is higher at last stages due to the stronger IBI while it is lower at early stages, resulting in higher error rate for the symbols near the end of the $N_{c}$-symbol block. Therefore, only the reliable $X$-symbol block at early stages is picked up from the detected block.

3 Computer Simulation Results

The performance of SC-MIMO spatial multiplexing using iterative overlap QRM-MLBD is evaluated by computer simulation. The simulation condition is summarized in Table 1. 16QAM is used for data modulation. We assume $N_{t}=2, N_{r}=2$, and a frequency-selective quasi-static Rayleigh fading channel with an $L=16$-path uniform power delay profile. Ideal channel estimation is assumed. In this paper, SC-MIMO packet transmission is considered, where one packet is composed of 384 symbols.

Table 1 Computer simulation condition

3.1 Throughput Performance

Figure 4 plots the throughput performance as a function of average received $E_{s}/N_{0}$ for $N_{c}=64, X=4\sim 48, I=0$ and 1, and $M=16; X$ is the number of symbols to be picked up and $M$ is the number of surviving paths in the M-algorithm. In this paper, the throughput is defined as $N_{t}\hbox {log}_{2}Z\times (1-\hbox {PER})/(1+N_{g}/N_{c})$, where $Z$ is the modulation level and PER denotes the packet error rate. The throughput performance of the conventional QRM-MLBD with CP insertion is also plotted for comparison. The training sequence (TS) aided QRM-MLBD with TS length of 16 symbols [9] is used, which is similar to the conventional QRM-MLBD with CP insertion. It can be seen from Fig. 4 that iterative overlap QRM-MLBD improves the throughput performance when smaller $X$ is used. This is because at early stages of M-algorithm, the IBI from the next block is less significant. However, the use of smaller $X$ increases the detection complexity. It can also be seen that iterative processing improves the throughput even if large $X$ is used. With no iteration $(I=0), X=4$ should be used to improve the throughput performance sufficiently. However, when $I =1$, a much larger $X$ (e.g, $X=48$) can be used. Since iterative overlap QRM-MLBD does not require the CP insertion, the peak throughput is higher than that of the conventional QRM-MLBD with CP insertion.

Fig. 4

Throughput performance. a $I=0$. b $I=1$

3.2 Computational Complexity

The computational complexity of iterative overlap QRM-MLD is discussed. The computational complexity here is defined as the number of complex multiplications per symbol. The computational complexity for the iterative overlap QRM-MLBD and the conventional QRM-MLBD with CP insertion (TS-aided QRM-MLBD) are shown in Table 2. Time-domain signal processing is also implemented in TS-aided QRM-MLBD.

Table 2 Number of complex multiplications per symbol

The overall computational complexity per symbol is shown in Fig. 5 as a function of the number of iterations $I$ for $N_{c}=64$ and $M=16$. As we mentioned in the previous section, $X=4$ should be used to sufficiently improve the throughput performance with no iteration $(I=0)$ and $X=48$ can be used when $I=1$. Therefore, $X$ is set to 4 and 48 for $I=0$ and 1, respectively. When $I=2,\; X=48$ is also required. The overall computational complexity of the conventional QRM-MLBD with CP insertion is also plotted for reference. Since iterative processing improves the throughput even if large $X$ is used, the overall computational complexity can be reduced even if iterative processing is introduced when $N_{c}=64$.

Fig. 5

Impact of $I$ on the overall computational complexity

In the next, we discuss the relationship between the observation window size ($N_{c}+L$-1 symbols) and the overall computational complexity. Figure 6 plots the overall computational complexity as a function of $N_{c}$ when the best combination of $I$ and $X$is used to achieve a throughput of 8bps/Hz at $E_{s}/N_{0}=22\hbox {dB}$. When a smaller $N_{c}$ is used, larger $I$ and smaller $X$ are needed. Therefore, the computational complexity of the IBI cancellation, computation of ${\hat{\mathbf{Y}}}^{(i)}$ as well as path metric computation increases (because of larger $I$ and smaller $X)$. On the other hand, since the size of the channel matrix is small (the size of equivalent channel matrix is $N_{r}(N_{c}+L-1)\times N_{t}N_{c})$, the computational complexity of QR decomposition reduces. It is understood from Fig. 6 that the overall computational complexity to achieve a peak throughput of 8bps/Hz is lowest when $N_{c}=28$ and is about 50 % of the conventional QRM-MLBD $(N_{c}=64)$ with CP insertion.

Fig. 6

Impact of $N_{c}$ on the overall computational complexity

4 Conclusion

In this paper, we proposed a time-domain iterative overlap QRM-MLBD which requires no CP insertion for SC-MIMO spatial multiplexing. To extend our previously proposed iterative overlap QRM-MLBD to the MIMO systems, we introduce an appropriate modification of the stacked received symbol vector of SC-MIMO spatial multiplexing. Remembering that the IBI is significant near the bottom of the elements in the modified stacked received symbol vector and the residual IBI is significant near the end of the detected symbol block after QRM-MLBD, only the reliable $X$ symbols are picked up after performing QRM-MLBD. To detect a continuously transmitted symbol stream, the present observation window for performing QRM-MLBD is overlapped with the previous and the next observation windows. To further improve the detection performance, iterative processing was introduced. It has been showed that the proposed iterative overlap QRM-MLBD improves the throughput by 25 % than the conventional QRM-MLBD with CP insertion $(N_{c}=64,\; N_{g}=16)$. The overall computational complexity can be reduced to 50 % when compared with the conventional QRM-MLBD with CP insertion $(N_{c}=64)$.