1 Introduction and motivation

Cover and El Gamal stated, in their pioneering paper in 1979, that the full understanding of the relay channel would yield the capacity of the single sender single receiver general relay network (in Fig. 7 in [3]). They anticipated that this unknown capacity would be an information theoretic generalization of the well-known max-flow min-cut theorem. However, as of 2021, i.e., after 42 years, we are very far from this “foreseen” goal: The capacity of the relay channel, even the simplest Gaussian relay network with a single source, single destination and a relay, is still unknown [4], and the interference channel’s capacity region—even without a relay—is still an open problem [5]. In short, except for the simplest networks like Gaussian SIMO and MISO channels, the capacity region of most Gaussian networks is still unknown [4, 5].

Speaking strictly, the only available upper bound on the capacity of the Gaussian relay channel is the cut-set bound developed by Cover and El Gamal in 1979 [3]. The cut-set bound has been consistently used as a benchmark for performance of various relay networks (see e.g. [5,6,7,8,9,10,11,12,13,14,15,16,17]) since 1970s. In order to turn the challenging Gaussian networks capacity problems into mathematically tractable frameworks, various simplifications have been suggested in recent years. Avestimehr, Diggavi and Tse have introduced a deterministic approach and a deterministic model for analyzing the capacity of wireless relay networks [5, 8, 18, 19]. Although their linear deterministic network model is discrete and deterministic like traditional wireline network models, it has attracted a great attention because it captures certain physical aspects of wireless communications such as broadcasting and interference. They show that the capacity of Gaussian relay networks can be closely approximated by the cut-set bound, and more precisely, the gap between the cut-set bound and capacity in these networks can be bounded by a function that grows linearly with the number of nodes in the network [5, 8, 18, 19].

In [7], the authors present an improved lower bound on the rate achieved by the compress-and-forward based strategies in arbitrary Gaussian relay networks. In [4], the authors develop a new upper bound on the capacity of the Gaussian primitive relay channel which is tighter than the cut-set bound. Various approximation approaches [5, 8, 18, 20, 21] in wireless information theory recently focus on bounding the gap of the achievable strategies to the cut-set bound of the network. A large scale multi-level relay network has been analyzed in [22]. A combinatorial study of linear deterministic relay networks is presented in [23].

Most of the existing literature exclusively focus on developing achievable strategies for the relay channel as well as larger relay networks [4]. Consequently, an abundant number of methods on relaying schemes have been developed over the last decade, such as decode-and forward, compress-and-forward, amplify-and-forward, compute-and-forward, quantize-map-and-forward, noisy network coding, etc. [20, 26,27,28,29,30,31,32, 34, 35]. However, all these relaying schemes are out of the scope of this paper, and here we focus on the min-cut capacity bounds for general Gaussian N-relay networks.

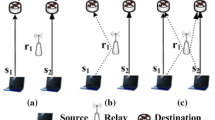
Nazaroğlu et.al. [24] examine the Gaussian N-relay diamond network and also present an upper bound to its capacity in terms of the capacities of SIMO and MISO channels inside the network. Our motivation of this paper is to extend the wireless network simplification in [24] to a more general relay network: Nazaroğlu et. al. in [24] assume that the source node can only transmit to the relay nodes over broadcast channel and the relay nodes can only transmit to the destination node over a multi-access channel. However, in this paper, we assume that (i) the relay nodes can transmit among themselves and (ii) there is a direct channel between the source node and the destination node.

On the other hand, the GADIA in [2] has become a pioneering algorithm in the wireless interference avoidance literature recently. The author in [1] shows that the basic GADIA [2] with only 2-channels actually performs a max-cut partitioning of corresponding channel gain matrix.

1.1 Main contributions of this paper

Our main contributions in this paper are as follows: Using the results of the diamond network in [24] and the recent results in [1], we

  1. (i)

    present a Gaussian N-relay network by allowing relays to communicate to each other and allowing a direct channel between source and destination. The standard N-Relay diamond network [24] is a special case of the presented N-Relay general network.

  2. (ii)

    propose a modified GADIA-based algorithm to find the min-cut capacity bound of the Gaussian N-relay network. The proposed modified GADIA-based simple algorithm enables the N-relay network to determine the relay clusters in a distributed manner.

  3. (iii)

    present an upper and a lower bound to its min-cut capacity using the modified basic GADIA algorithm. The proposed bounds are relatively tight to the min-cut capacity bound.

  4. (iv)

    show that the modified GADIA-based capacity upper bounds give an insight into whether allowing the relays to communicate to each other pays off the extra channel uses or not.

The manuscript is arranged as follows: Related work in [24] and the basic GADIA [2] is summarized in Sect. 2. We present our main results, i.e., the upper bound and the modified-GADIA, in Sect. 3. Simulation results are shown in Sect. 4, followed by the conclusions in Sect. 5.

2 Related work

The traditional Gaussian N-Relay diamond network [24] is shown in Fig. 1. The received signals are obtained in terms of the transmitted signal and the channel gains as follows:

$$\begin{aligned} & Y_{i} \left[ t \right] = h_{i,s} X_{s} \left[ t \right] + Z_{i} \left[ t \right] \\ & Y_{d} \left[ t \right] = \mathop \sum \limits_{{j \in{\boldsymbol{\varLambda}}}} h_{d,j} X_{j} \left[ t \right] + Z\left[ t \right] \\ \end{aligned}$$
(1)

where \({h}_{i,s}\) represents the complex coefficient from the source to the relay node i; and \(h_{di}\) denotes the complex channel gain from the node i to the destination node d. \(Z_{i} \left[ t \right]{, }i = 1, \cdots ,N\), and \(Z\left[ t \right]\) are independent and identically distributed circularly symmetric Gaussian random variables of variance \(\sigma^{2}\). Without loss of generality and for the sake of brevity, we assume that the transmit powers of all nodes are the same and equal to P, and \(SNR = P/\sigma^{2}\) [24].

Fig. 1
figure 1

A Gaussian N-Relay diamond network (does not allow relays to communicate to each other)

Full size image

Capacity of the Gaussian N-Relay diamond network in Fig. 1 is investigated in [24] and [25]. A cut divides the network into two sets \(\left\{ {s,{\boldsymbol{\varLambda}}} \right\}\) and \({\text{\{ }}\overline{\boldsymbol{\varLambda }},d\}\) where s represents source, d is destination, set \({\boldsymbol{\varLambda}}\) includes the indices of the relays in the first set, and set \(\overline{\boldsymbol{\varLambda }}\) includes the indices of the other relays which are in the second set. For any cut, the maximization of the mutual information can be upper bounded by the capacities of the SIMO (single input multiple output) channel between source and relays in set \(\overline{\boldsymbol{\varLambda }}\) and MISO (multiple input single output) channel between relays in \({\boldsymbol{\varLambda}}\) and destination d [24]. Therefore

$$C \le \overline{C} = \mathop {max}\limits_{{X_{S} ,X_{1} , \cdots ,X_{N} ,}} \mathop {min}\limits_{{{\boldsymbol{\varLambda}}\subseteq \left[ N \right]}} I\left( {X_{S} ,X_{{\boldsymbol{\varLambda}}} ;{ }Y_{d} ,Y_{{\overline{\boldsymbol{\varLambda }}}} |X_{{\overline{\boldsymbol{\varLambda }}}} } \right)$$
(2)

From [24], Eq. (9) on p.6333, we write the upper bound for the network in Fig. 1.

$$\overline{C} \le \mathop {min}\limits_{{{\boldsymbol{\varLambda}}\subseteq \left[ N \right]}} \left( {C_{SIMO} \left( {s;\overline{\boldsymbol{\varLambda }}} \right) + C_{MISO} \left( {{\boldsymbol{\varLambda}};d} \right)} \right)$$
(3)

Naturally the simplest case is 1-relay network (i.e. N = 1). Obviously, this 1-relay scenario has two possible meaningful cuts: These two cuts include some well-known results like the upper-bound in [16], Eq. (18), and the achievable rate \(R_{DF}\) in [8], Appendix A, page 1897, and the upper bound in [13], Eq. (11), page 2022 (taking zero correlation between the source and relay outputs \(X_{1}\) and \(X_{2}\), i.e. taking \(\beta = 0\) [13]), among others. Considering the relays-receive period \(\alpha D\) and relays-transmit period \(\left( {1 - \alpha } \right)D\) in Time Division mode in [13], two possible cuts are given in [13], Eqs. (10) and (11), page 2022, as follows

$$C_{1}^{ + } = \frac{\alpha }{2}\log \left( {1 + \left| {h_{dS} } \right|^{2} + \left| {h_{1S} } \right|^{2} } \right) + \frac{1 - \alpha }{2}\log \left( {1 + \left| {h_{dS} } \right|^{2} } \right)$$
(4)
$$C_{2}^{ + } = \frac{\alpha }{2}\log \left( {1 + \left| {h_{dS} } \right|^{2} } \right) + \frac{1 - \alpha }{2}\log \left( {1 + \left| {h_{dS} } \right|^{2} + \left| {h_{S1} } \right|^{2} } \right){ }$$
(5)

both of which are special cases of (3). A very similar result in Frequency Division mode is presented in [8].

On the other hand, the GADIA [2] has been one of the pioneering algorithms in the wireless interference avoidance literature. In this paper, in Sect. 3, we will propose a modified simple GADIA for determining the min-cut capacity bound for the general relay network. Therefore, for the readers’ convenience, in what follows we first summarize how the basic GADIA [2] works for 2-channel case.

2.1 Basic GADIA [2] with 2-channel case

Definition

Total Co-channel (Intra-Set) Interference for 2-Channel Case: Putting the relays into sets \(\overline{\boldsymbol{\varLambda }}_{t}\) and \({\boldsymbol{\varLambda}}_{t}\) at time t, we define the Total Co-channel (Intra-Set) Interference \(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot}\) as follows:

$$I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right) = { }I_{{\overline{\boldsymbol{\varLambda }}}}^{tot} \left( t \right) + I_{{\boldsymbol{\varLambda}}}^{tot} \left( t \right) = \underbrace {{\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }}_{t} ,d} \right\}}} \mathop \sum \limits_{{j \in \left\{ {\overline{\boldsymbol{\varLambda }}_{t} ,d} \right\}}} \left| {h_{ij} } \right|^{2} }}_{{Total\,\,Interf.\,\,in\,set\,\,\overline{\boldsymbol{\varLambda }}}} + \underbrace {{\mathop \sum \limits_{{i \in \left\{ {{\varvec{s}},{\boldsymbol{\varLambda}}_{t} } \right\}}} \mathop \sum \limits_{{j \in \left\{ {{\varvec{s}},{\boldsymbol{\varLambda}}_{t} } \right\}}} \left| {h_{ij} } \right|^{2} }}_{{Total\,Interf.\,{ }in\,\,set\,\,{\boldsymbol{\varLambda}}}}$$
(6)

where \(h_{ii} = 0.\) Let’s assume there are N transmitters to be allocated to 2 channels only (and \(N > 2\)). The deterministic basic GADIA for 2-set case is given by Table 1. Representing the co-channel interference of channel 1 and channel 2 for node n at time t as \(I_{{\boldsymbol{\varLambda}}}^{n} \left( t \right)\) and \(I_{{\overline{\boldsymbol{\varLambda }}}}^{n} \left( t \right)\), respectively, where n = 1,2, …, N, the deterministic basic GADIA [2] assigns the node n to the following channel

$$x_{n} \left( {t + 1} \right) = index{\text{ min }}\left\{ {I_{{\boldsymbol{\varLambda}}}^{n} \left( t \right), I_{{\overline{\boldsymbol{\varLambda }}}}^{n} \left( t \right)} \right\}$$
(7)

where channel index \(x_{n} \left( {t + 1} \right) \in \left\{ {\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}} \right\}\). From the analysis in [2], each time a node changes its channel by Eq. (7) the total co-channel interference is further decreased:

$$I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( {t + 1} \right) < I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)$$
(8)
Table 1 The deterministic basic GADIA [2] for 2-channel case
Full size table

For the details of the proof, see [2]. The basic GADIA performs in a distributed fashion in such a way that each node is allocated only using its interference measurements. How the basic GADIA [2] works for relay n at arbitrary step number t in a 2-channel case is illustrated in Fig. 3. It is very recently shown in [1] (Proposition 5 and Corollary 4) that the basic GADIA [2] actually performs the max-cut of the corresponding graph for the 2-channel case. For further details, see [1]. An extension to the complex graph case has very recently been presented in [33].

3 Main results

3.1 Network model

Our model is based on the model in [24]. The main difference is as follows: In the traditional Gaussian N-Relay diamond network in [24] (see Fig. 1) the source only transmits to the relays and the relays transmit only to the destination (and there is no direct channel between the source and destination). However, in our network model, relays can also transmit to each other if/when needed and direct channel between the source and destination also exists as seen in Fig. 2. Our motivation for this extension is twofold: (i) to unleash the potential of the unused channels in full-duplex relay networks, and (ii) to generalize the network in [24].

Fig. 2
figure 2

Gaussian N-relay general network (allows relays to communicate to each other)

Full size image

Using the model and notation in [24] for the general relay network in Fig. 2, the received signals are obtained in terms of the transmitted signal and the channel gains as follows:

$$\begin{aligned} & Y_{i} \left[ t \right] = \mathop \sum \limits_{{j \in T_{i} }} h_{i,j} X_{j} \left[ t \right] + Z_{i} \left[ t \right] \\ & Y_{d} \left[ t \right] = \mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} h_{dj} X_{j} \left[ t \right] + Z\left[ t \right] \\ \end{aligned}$$
(10)

where \(T_{i}\) represents the set of indices of the transmitting relays when the relay node i is the receiver, and \(T_{i} \subseteq \left\{ {s,1,2, \cdots ,N} \right\}\), and \(h_{is}\) represents the complex channel gain from the source to the relay node i; and \(h_{di}\) denotes the complex channel gain from the node i to the destination node d. \(Z_{i} \left[ t \right]{, }i = 1, \cdots ,N\), and \(Z\left[ t \right]\) are independent and identically distributed circularly symmetric Gaussian random variables of variance \(\sigma^{2}\). Without loss of generality and for the sake of brevity, we assume that the transmit powers of all nodes are the same and equal to P, and we define \(SNR = P/\sigma^{2}\) as in [24]. We examine the maximum reliable communication rate C in bits/channel use that can be achieved between the source node and the destination node in a generalized Gaussian N-relay network. First we define “squared channel gain matrix/graph” for the N-relay general network.

Definition

For the standard N-relay diamond network (which does not allow relays to communicate to each other), the following (N + 2) × (N + 2) dimensional (partially full) matrix is called “diamond squared channel gain matrix”.

$${\varvec{A}}_{d}={\left[\begin{array}{c} \, \, 0 \, \, \, \, \, {\left|{h}_{1s}\right|}^{2} \, \, \, \, \, {\left|{h}_{2s}\right|}^{2} \, \, \cdots \, \, {\left|{h}_{Ns}\right|}^{2} \, \, \, \, \, 0\\ {\left|{h}_{1s}\right|}^{2} \, \, \, \, \, 0 \, \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \cdots \, \, \, \, \, \, {0} \, \, \, \, \, \, {\left|{h}_{d1}\right|}^{2}\\ \, \, \, \vdots \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \vdots \\ {\left|{h}_{Ns}\right|}^{2} \, \, \, \, 0 \, \, \, \, \, \, \, \, \, {0} \, \, \, \, \, \cdots \, \, \, \, \, \, {0} \, \, \, \, \, {\left|{h}_{dN}\right|}^{2}\\ \, \, 0 \, \, \, \, \, \, {\left|{h}_{d1}\right|}^{2} \, \, \, \, {\left|{h}_{d2}\right|}^{2} \cdots \, \, \, {\left|{h}_{dN}\right|}^{2} \, \, \, 0\end{array}\right]}_{\left(N+2\right)\times \left(N+2\right)}$$
(11)

Most of the entries in matrix \({{\varvec{A}}}_{d}\) in (11) are zero because relays cannot transmit to each other in the traditional N-relay diamond network [24].

Definition

The following (N + 2) × (N + 2) dimensional matrix is called “squared channel gain matrix” for N-Relay general network:

$${\varvec{A}}_{g}={\left[\begin{array}{c} \, \, 0 \, \, \, \, \, \, {\left|{h}_{1s}\right|}^{2} \, \, \, \, {\left|{h}_{2s}\right|}^{2} \, \, \cdots \, \, {\left|{h}_{Ns}\right|}^{2} \, \, \, \, {\left|{h}_{ds}\right|}^{2}\\ {\left|{h}_{1s}\right|}^{2} \, \, \, \, \, 0 \, \, \, \, \, \, \, {\left|{h}_{12}\right|}^{2} \, \, \cdots \, \, {\left|{h}_{2N}\right|}^{2} \, \, \, \, {\left|{h}_{d1}\right|}^{2}\\ \, \, \, \vdots \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \vdots \, \, \, \, \, \, \, \, \, \, \, \, \vdots \\ {\left|{h}_{Ns}\right|}^{2} \, \, {\left|{h}_{N1}\right|}^{2} \, \, {\left|{h}_{N2}\right|}^{2} \, \, \cdots 0 \, \, \, \, \, \, \, \, \, {\left|{h}_{dN}\right|}^{2}\\ {\left|{h}_{ds}\right|}^{2} \, \, {\left|{h}_{d1}\right|}^{2} \, \, \, \, {\left|{h}_{d2}\right|}^{2} \cdots \, \, {\left|{h}_{dN}\right|}^{2} \, \, \, \, \, 0\end{array}\right]}_{\left(N+2\right)\times \left(N+2\right)}$$
(12)

i.e., \({\left[{{\varvec{A}}}_{g}\right]}_{ij}=\left\{\begin{array}{c}0, \, \, \, \, \, \, \, \, \, i=j\\ {\left|{h}_{ij}\right|}^{2}\text{,} \, \, \, \, \, i\ne j\end{array}\right.\) where \(i,j\in \left\{s,\mathrm{1,2},\cdots ,N,d\right\}\).

Comparing (11) with (12), the general N-relay network’s matrix \({{\varvec{A}}}_{g}\) is a full matrix (with zero diagonal) unlike the diamond N-relay network’s matrix \({{\varvec{A}}}_{d}\).

Definition

Cut of Interference matrix is defined as follows

$$J_{{\user2{\overline{\varLambda }\varLambda }}}^{{}} \left( t \right) = \mathop \sum \limits_{{i \in \left\{ {s, {\boldsymbol{\varLambda}}_{t} } \right\}}} \mathop \sum \limits_{{j \in \left\{ {\overline{\boldsymbol{\varLambda }}_{t} ,d} \right\}}} \left| {h_{ij} } \right|^{2}$$
(13)

3.2 Modified GADIA

A very recent paper [1] shows that the deterministic basic GADIA [2] with the interference matrix \({\varvec{A}}_{g}\) in (12) performs max-cut of the corresponding graph. However, we need min-cut for determining the relay network’s cut-set capacity bound. How can we modify the basic GADIA in [2] so that it performs min-cut instead of max-cut? In what follows, we present a modified and constrained simple GADIA to perform the min-cut of the interference matrix \({\varvec{A}}_{g}\) in (12).

In the proposed modified GADIA (14), we have the negative sign to turn the max-cut problem into the min-cut problem. If we do not introduce any constraints, then this change would eventually give us the trivial solution where the cut would finally vanish, i.e., all relays would be assigned to the same set, which is practically meaningless. To avoid this trivial solution, we need to introduce the constraint that \(N_{{\boldsymbol{\varLambda}}} \ne 0\) and \(N_{{\overline{\boldsymbol{\varLambda }}}} \ne 0\) and \(N_{{\boldsymbol{\varLambda}}}\) and \(N_{{\overline{\boldsymbol{\varLambda }}}}\) are close to each other, i.e., the number of relays in set \({\boldsymbol{\varLambda}}\) and the number of relays in set \(\overline{\boldsymbol{\varLambda }}\) are close to each other.

Proposition 1

For a given general relay network in Fig. 2with the channel gains in (12), the proposed modified algorithm in Table 2minimizes the cut \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) in (13).

Table 2 Proposed modified and constrained GADIA
Full size table

Proof

From (6), (12) and (13),

$$\left| {{\varvec{A}}_{g} } \right|_{1} = {\text{constant}} = 2I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right) + 2J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)$$
(15)

where \(\left| {{\varvec{A}}_{g} } \right|_{1}\) represents the 1-norm of matrix \({\varvec{A}}_{g}\), which is constant. Now let’s take an arbitrary relay n in set \(\overline{\boldsymbol{\varLambda }}\). The total intra-set interference in \({\boldsymbol{\varLambda}}\) and \(\overline{\boldsymbol{\varLambda }}\), i.e., \(I_{{\boldsymbol{\varLambda}}}^{tot}\), and \(I_{{\overline{\boldsymbol{\varLambda }}}}^{tot}\), respectively, at an arbitrary time t is equal to

$$I_{{\overline{\boldsymbol{\varLambda }}}}^{tot} \left( t \right) = \mathop{\underbrace {{2I_{{\overline{\boldsymbol{\varLambda }}}}^{n}}}_{{{\text{related}}\,{\text{to}}}}}\limits_{{\text{relay}}\,n} + \mathop{\mathop{\underbrace{{I_{{\overline{\boldsymbol{\varLambda }}}}^{others} \left( t \right)}}_{{{\text{all }}\,{\text{other}}}}}\limits_{{\text{terms}}\,{\text{in}}\,{ }\overline{\boldsymbol{\varLambda}}}}\limits_{(not\,related\,to\,relay\,n)}$$
(16)

where \(I_{{\overline{\boldsymbol{\varLambda }}}}^{n} = \mathop \sum \limits_{{j \in \left\{ {\overline{\boldsymbol{\varLambda }}_{t} ,d} \right\}}} \left| {h_{nj} } \right|^{2}\) as shown in Fig. 3. If relay n is allocated from set \(\overline{\boldsymbol{\varLambda }}\) to \({\boldsymbol{\varLambda}}\), then

$$\begin{aligned} & I_{{\overline{\boldsymbol{\varLambda }}}}^{tot}\left( {t + 1} \right) = I_{{\overline{\boldsymbol{\varLambda}}}}^{others} \left( t \right),\quad {\text{and}} \\ &I_{{\boldsymbol{\varLambda}}}^{tot} \left( {t + 1} \right) = \mathop{\underbrace{{2I_{{\boldsymbol{\varLambda}}}^{n}}}_{{{\text{due}}\,{\text{to}}}}}\limits_{{\text{relay}}\,n} +I_{{\boldsymbol{\varLambda}}}^{tot} \left( t \right) \end{aligned}$$
(17)
Fig. 3
figure 3

An illustration of the basic GADIA [2] for relay n at arbitrary step number t in a 2-set case

Full size image

where \(I_{{\boldsymbol{\varLambda}}}^{n} = \mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left| {h_{nj} } \right|^{2}\). From (6), (14), (16) and (17), the proposed modified GADIA gives

$$I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( {t + 1} \right) > I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)$$
(18)

Similarly, it is straightforward to show that if a relay in \({\boldsymbol{\varLambda}}\) is assigned to \(\overline{\boldsymbol{\varLambda }}\) by the proposed algorithm (14), then the total interference is strictly further increased, i.e., \(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( {t + 1} \right) > I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\). From (15), an increase in \(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\) causes the cut \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) to decrease. Because the cut \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) is finite, we conclude that the proposed modified GADIA in Table 2minimizes the cut \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) in (13), which completes the proof. □

3.3 Comparison of the basic GADIA [2] and the Modified GADIA

It is recently shown in [1] that the basic GADIA [2] in (9) performs max-cut for the positive interference matrix \({\varvec{A}}_{g}\) in (12). So, the GADIA [2] yields the minimum total interference (\(\min {\text{of}}I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\) in (6)) in the relay network. However, the proposed modified and constraint GADIA does exactly the opposite: The modified GADIA in Table 2 aims at temporarily maximizing the total interference in the relay network for a short time duration just in order to determine the sets \({\boldsymbol{\varLambda}}\) and \(\overline{\boldsymbol{\varLambda }}\) which are needed to find the min-cut capacity bound. In summary, the proposed modified GADIA fully loads the relay network by maximizing the total network interference (\(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\) in (6)) so that the cut-set bound of the relay network is “discovered” in a distributed fashion.

3.4 Low SNR case

Proposition 2

In the low-SNR regime, the proposed simple modified-GADIA algorithm in Table 2 for the “squared channel gain matrix” in (12) yields an upper bound to the mutual information between the source and destination in the Gaussian N-relay network in Fig. 2.

Proof

Applying the max-flow min-cut theorem to the Gaussian general N-relay network in Fig. 2, and following the steps in [24], Appendix A, page 6338, we obtain

$$\begin{aligned} \overline{C} & \le \mathop {min}\limits_{{{\boldsymbol{\varLambda}}\subseteq \left[ N \right]}} \mathop {sup}\limits_{{X_{S} ,X_{{\boldsymbol{\varLambda}}} ,X_{{\overline{\boldsymbol{\varLambda }}}} ,}} I\left( {X_{S} ,X_{{\boldsymbol{\varLambda}}} ; Y_{d} ,Y_{{\overline{\boldsymbol{\varLambda }}}} |X_{{\overline{\boldsymbol{\varLambda }}}} } \right) \\ { } & \le \mathop {min}\limits_{{{\boldsymbol{\varLambda}}\subseteq \left[ N \right]}} \mathop {sup }\limits_{{X_{S} }} I\left( {X_{S} ;Y_{{\overline{\boldsymbol{\varLambda }}}} } \right) + \mathop {\sup }\limits_{{X_{{\boldsymbol{\varLambda}}} }} I\left( {X_{{\boldsymbol{\varLambda}}} ;Y_{d}^{{\boldsymbol{\varLambda}}} } \right) \\ { } & \le \mathop {min}\limits_{{{\boldsymbol{\varLambda}}\subseteq \left[ N \right]}} \left( {\left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} C_{SIMO} \left( {j;\overline{\boldsymbol{\varLambda }}} \right)} \right] + C_{MISO} \left( {\left\{ {s,{\boldsymbol{\varLambda}}} \right\};d} \right)} \right) \\ \end{aligned}$$
(19)

where \({Y}_{d}^{\boldsymbol{\varLambda }}={\sum }_{i\in \left\{s,\boldsymbol{\varLambda }\right\}}{h}_{di}{X}_{i}\). Thus

$$C_{MISO} \left( {\left\{ {s,\varLambda } \right\};d} \right) = \log \left( {1 + SNR\left( {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left| {h_{d,j} } \right|^{2} } \right)} \right)$$
(20)

Unlike the diamond network in [24], allowing the relays to transmit to each other results in extra \({N}_{\boldsymbol{\varLambda }}\) SIMO channels as seen from Fig. 2. We allocate these inter-relay SIMO channels in \({N}_{\boldsymbol{\varLambda }}\) orthogonal sub timeslots/frequencies so that during each sub timeslot/frequency we realize one interference-free SIMO channel. This results in \({N}_{\boldsymbol{\varLambda }}\) extra channel uses as compared to that in [24]. From Fig. 2.

$$\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} C_{SIMO} \left( {j;\overline{\boldsymbol{\varLambda }}} \right) = \mathop \sum \limits_{{j \in \left\{ {s,\varLambda } \right\}}} \log \left( {1 + SNR\left( {\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }}} \right\}}} \left| {h_{i,j} } \right|^{2} } \right)} \right)$$
(21)

From (20) and (21), we have

$$\begin{aligned} \overline{C} & \le \frac{1}{L}\left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \log \left( {1 + SNR\left( {\mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,j} } \right|^{2} } \right)} \right)} \right] \\ { } & \quad + \,\frac{1}{L}\log \left( {1 + SNR\left( {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left| {h_{d,j} } \right|^{2} } \right)} \right) \\ \end{aligned}$$
(22)

where L is the total number of channel uses. Allowing inter-relay \(N_{{\boldsymbol{\varLambda}}}\) SIMO channels yields extra \(N_{{\boldsymbol{\varLambda}}}\) channel uses, and therefore \(L = N_{{\boldsymbol{\varLambda}}} + 2\), where 2 represents the channel use of SIMO from source to \(\overline{\boldsymbol{\varLambda }}\) and the channel use of MISO from \({\boldsymbol{\varLambda}}\) to destination. Considering the low SNR regime, i.e. \(\log \left( {1 + x} \right) \approx x\) in Eq. (11), we obtain

$$\overline{C} \le \frac{1}{L}SNR\left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left( {\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} \left| {h_{i,j} } \right|^{2} } \right)} \right]$$
(23)

Examining the upper bound in (23), we see that the capacity upper bound (23) is equal to the min-cut of the graph represented by the matrix \({{\varvec{A}}}_{g}\) in (12), i.e.,

$$C^{ + } = \frac{1}{L}\min \left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left( {\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} \left| {h_{i,j} } \right|^{2} } \right)} \right] = \frac{1}{L}min \,cut\left( {A_{g} } \right)$$
(24)

From Proposition 1 above, Eqs. (19) and (24), we conclude that the proposed simple modified-GADIA algorithm in Table 2 for the “squared channel gain matrix” in (12) yields an upper bound to the mutual information between the source and destination in the Gaussian N-relay general network in Fig. 2, which completes the proof. □

In summary, the min-cut capacity bound in (3) for the standard diamond relay network is obtained by two channel uses (timeslots/frequencies), and thus

$$UB_{diamond} = \frac{1}{2}C_{SIMO} \left( {s;\overline{\boldsymbol{\varLambda }}} \right) + \frac{1}{2}C_{MISO} \left( {{\boldsymbol{\varLambda}};d} \right)$$
(25)

On the other hand, the min-cut capacity upper bound in (19) for the proposed general relay network is

$$UB_{general} = \frac{1}{L}\mathop \sum \limits_{{j \in \left\{ {s,\varLambda } \right\}}} C_{SIMO} \left( {j;\overline{\boldsymbol{\varLambda }}} \right) + \frac{1}{L}C_{MISO} \left( {\left\{ {s,{\boldsymbol{\varLambda}}} \right\};d} \right)$$
(26)

Comparing (25) and (26), there is a trade-off between the increased channel uses (because \(L\ge 3\)) and the min-cut capacity bound. Do the extra channel uses pay off or not? The answer is that it depends on the inter-relay channel gains as follows (for the low SNR case). From (25), (26) and (24), we have

$$\underbrace {{\frac{1}{2}\left( {\mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,s} } \right|^{2} + \mathop \sum \limits_{{j \in \left\{{\boldsymbol{\varLambda}}\right\}}} \left| {h_{d,j} } \right|^{2} } \right)}}_{{diamond\,\,relay\,\,network\,\,in\,\left[ {24} \right]}} \,\,{\text{versus }}\,\,\underbrace {{\frac{1}{L}\left( {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left( {\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} \left| {h_{i,j} } \right|^{2} } \right)} \right)}}_{proposed\,\,general\,\,relay\,\,network}$$
(27)

Using \(\frac{1}{2}=\frac{1}{L}+\frac{L-2}{2L}\) and the SIMO channels among the relays (from each relay in set \({\boldsymbol{\varLambda}}\) to all relays in set \(\overline{\boldsymbol{\varLambda }}\)) in the right side of (27), we obtain the following result: If

$$\frac{L - 2}{{2L}}\left( {\left( {C_{SIMO} \left( {s;\overline{\boldsymbol{\varLambda }}} \right) + C_{MISO} \left( {{\boldsymbol{\varLambda}};d} \right)} \right)} \right) < \frac{1}{L}\left( {\left| {h_{d,s} } \right|^{2} + \mathop \sum \limits_{i \in \varLambda } C_{SIMO} \left( {i;\overline{\boldsymbol{\varLambda }}} \right)} \right)$$
(28)

or equivalently, if

$$\frac{L - 2}{{2L}}\left( {\mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,s} } \right|^{2} + \mathop \sum \limits_{{j \in \left\{{\boldsymbol{\varLambda}}\right\}}} \left| {h_{d,j} } \right|^{2} } \right) < \frac{1}{L}\left( {\left| {h_{d,s} } \right|^{2} + \mathop \sum \limits_{i \in \varLambda } \mathop \sum \limits_{{j \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,j} } \right|^{2} } \right)$$
(29)

then the min-cut capacity bound is increased. As long as the min-cut capacity bound is concerned, this shows that allowing the relays to communicate to each other pays off the extra channel uses if the condition in (29) is met. The left side of (29) is a portion of the standard diamond relay network’s min-cut capacity bound and the right side of (29) is due to the inter-relay channels which are not used in the diamond network. As an example, for the Gaussian generalized 3-relay network in Fig. 5 examined in Example 1, where \({\boldsymbol{\varLambda}}= \left\{ 3 \right\}\), and \(\overline{\boldsymbol{\varLambda }} = \left\{ {1,2} \right\}\), and \(L = 3\), if

$$\frac{1}{6}\left( {\left| {h_{1,s} } \right|^{2} + \left| {h_{2,s} } \right|^{2} + \left| {h_{d,3} } \right|^{2} } \right) < \frac{1}{3}\left( {\left| {h_{d,s} } \right|^{2} + \left| {h_{1,3} } \right|^{2} + \left| {h_{2,3} } \right|^{2} } \right)$$
(30)

then the min-cut capacity upper bound is increased, i.e. the inter-relay communication pays off in terms of the min-cut capacity bound for low SNR regime.

As another example, let’s assume a 4-Relay network where \({\boldsymbol{\varLambda}}= \left\{ {2,3} \right\}\), and \(\overline{\boldsymbol{\varLambda }} = \left\{ {1, 4} \right\}\), and thus \(L = 4\). From (29), if

$$\frac{1}{4}\left( {\left| {h_{1,s} } \right|^{2} + \left| {h_{4,s} } \right|^{2} + \left| {h_{d,2} } \right|^{2} + \left| {h_{d,3} } \right|^{2} } \right) < \frac{1}{4}\left( {\left| {h_{d,s} } \right|^{2} + \left| {h_{1,2} } \right|^{2} + \left| {h_{4,2} } \right|^{2} + \left| {h_{1,3} } \right|^{2} + \left| {h_{4,3} } \right|^{2} } \right)$$
(31)

then the min-cut capacity bound is further increased in the low SNR case.

3.5 High SNR case

Proposition 3

In the high-SNR regime, the mutual information between the source and destination in the Gaussian general N-relay network in Fig. 2admits an upper bound obtained by the proposed modified-GADIA algorithm in Table 2for the “squared channel gain matrix” in (12).

Proof

We observe the following tight upper bound to the sum of two log’s.

$$\log \left( {x_{i} } \right) + \log \left( {x_{j} } \right) \le \log \left( { x_{i} + x_{j} } \right) + \log \left( {\min \left\{ {x_{i} ,x_{j} } \right\}} \right),$$
(32)

where

$$0 < \left[ {\log \left( { x_{i} + x_{j} } \right) + \log \left( {\min \left\{ {x_{i} ,x_{j} } \right\}} \right) - \left( {\log \left( {x_{i} } \right) + \log \left( {x_{j} } \right)} \right)} \right] \le 1,$$
(33)

for any \({x}_{i},{x}_{j}\ge 2\). In (33) the maximum difference, which is 1, is obtained if and only if \({x}_{i}={x}_{j}\).Footnote 1

The presented bound in (32)–(33) plays a critical role in our derivations below for the high SNR case because (1) the proposed bound is tight and (2) it allows us to replace the sum of two log’s by the log of two sums. In order to give an insight into how tight the bound in (32) is, without loss of generality and the for the sake of brevity, we present an illustrative example with an arbitrary argument \({x}_{1}={2}^{9}={512}\) in Fig. 4. The argument of the other log function varies in the range \(2\le {x}_{2}\le 10000\). Figure 4 confirms that the proposed bound in (32)–(33) is indeed tight for any arguments \({x}_{1}\) and \({x}_{2}\) because in (32)–(33) what matters is the difference between the arguments \({x}_{1}\) and \({x}_{2}\) and not the absolute values of \({x}_{1}\) and \({x}_{2}\). The plots of Fig. 4(a, b) are the same, where argument \({x}_{2}\) is in linear scale and log scale in Fig. 4(a, b), respectively, for the sake of clarity. This is because the term \(\mathit{log}\left(\mathit{min}\left\{{x}_{i},{x}_{j}\right\}\right)\) strictly decreases and vanishes as the difference between the arguments \({x}_{1}\) and \({x}_{2}\) increases.

Fig. 4
figure 4

An illustrative example for Eqs. (32)–(33), \({{\varvec{x}}}_{1}={2}^{9}={512}\) and \(2\le {{\varvec{x}}}_{2}\le 10000\), a linear scale and b log scale

Full size image

Let’s define the following terms:

$${\text{for SIMOs}}\left\{ {\begin{array}{*{20}l} {G_{{\overline{\boldsymbol{\varLambda }},j}} = \mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,s} } \right|^{2} {, } \Rightarrow { }C_{{\overline{\boldsymbol{\varLambda }},j}} = {\text{log}}\left( {1 + G_{{\overline{\boldsymbol{\varLambda }},s}} } \right)} \hfill \\ {{ }\quad \quad \quad \quad j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}} \hfill \\ \end{array} } \right.$$
(34)

and

$${\text{for MISO}}\left\{ {\begin{array}{*{20}l} {G_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} = \mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left| {h_{d,j} } \right|^{2} } \\ { \Rightarrow { }C_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} = {\text{log}}\left( {1 + G_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} } \right)} \\ \end{array} } \right.$$
(35)

Using (26), (32), (34) and (35), we are able to upper bound the sum of log’s in (22) by the log of sums as follows:

$$\overline{C} \le \frac{1}{L}\left( {\log \left( {SNR\left[ {G_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} + \mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} G_{{\overline{\boldsymbol{\varLambda }},j}} } \right]} \right) + {\rm K}} \right),$$
(36)

where \({\rm K}\) has (\({N}_{\varLambda }+1\)) log terms, which are obtained by applying Eq. (32) \(\left({N}_{\varLambda }+1\right)\) times when we upper bound the sum of \(\left({N}_{\varLambda }+2\right)\) log’s by log of \(\left({N}_{\varLambda }+2\right)\) sums. From (34), (35) and (36), we obtain

$$\begin{aligned} \overline{C} & \le \frac{1}{L}\log \left( {SNR\left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left( {\mathop \sum \limits_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} \left| {h_{i,j} } \right|^{2} } \right)} \right]} \right) + \frac{\rm K}{L} \\ { } & \le \frac{1}{L}\log \left( {SNR\left[ {\min cut\left( {{\varvec{A}}_{g} } \right)} \right]} \right) + \frac{\rm K}{L} \\ \end{aligned}$$
(37)

From Proposition 1 above, (19) and (37), we conclude that the mutual information between the source and destination in the Gaussian general N-relay network in Fig. 2 admits an upper bound obtained by the proposed modified-GADIA algorithm in Table 2 for the “squared channel gain matrix” in (12), which completes the proof. □

In order to elaborate more about the constant K in (19), we give the following example: If N = 5, \({\boldsymbol{\varLambda}}= \left\{ {1,3} \right\}\), and \(\overline{\boldsymbol{\varLambda }} = \left\{ {2,4,5} \right\}\), then \({\rm K}\) in (36) is equal to the following:

$$\begin{aligned} {\rm K} & = \log \left( {SNR\min \left( {G_{{\overline{\boldsymbol{\varLambda }},s}} ,G_{{\overline{\boldsymbol{\varLambda }},1}} } \right)} \right) + \log \left( {SNR\min \left( {G_{{\overline{\boldsymbol{\varLambda }},3}} ,G_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} } \right)} \right) \\ & \quad + \,{\text{log}}\left( {SNR\min \left( {G_{{\overline{\boldsymbol{\varLambda }},s}} + G_{{\overline{\boldsymbol{\varLambda }},1}} { , }G_{{\overline{\boldsymbol{\varLambda }},3}} + G_{{d,\left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} } \right)} \right) \\ \end{aligned}$$
(38)

In what follows, we ask the same question as before: Does allowing the relays to communicate to each other pay off the extra channel uses or not for high SNR case? The answer is that it depends on the channel gains as shown below: Writing \(\frac{1}{2}=\frac{1}{L}+\frac{L-2}{2L}\) in (20)–(22) and using (34) and (35) yields the following result: If

$$\frac{L - 2}{{2L}}\left( {C_{SIMO} \left( {s;\overline{\boldsymbol{\varLambda }}} \right) + C_{MISO} \left( {{\boldsymbol{\varLambda}};d} \right)} \right) < \frac{1}{L}\left( {C_{MISO} \left( {\left\{ {s,{\boldsymbol{\varLambda}}} \right\};d} \right) + \mathop \sum \limits_{j \in \varLambda } C_{SIMO} \left( {j;\overline{\boldsymbol{\varLambda }}} \right)} \right)$$
(39)

or equivalently, if

$$\begin{aligned} & \frac{L - 2}{{2L}}\left( {\underbrace {{log\left( {1 + \mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,s} } \right|^{2} } \right)}}_{{C_{SIMO} \left( {s;\overline{\boldsymbol{\varLambda }}} \right)}} + \underbrace {{log\left( {1 + \mathop \sum \limits_{{j \in \left\{{\boldsymbol{\varLambda}}\right\}}} \left| {h_{d,j} } \right|^{2} } \right)}}_{{C_{MISO} \left( {{\boldsymbol{\varLambda}};d} \right)}}} \right) \\ & \quad < \frac{1}{L}\left( {\underbrace {{\mathop \sum \limits_{{j \in{\boldsymbol{\varLambda}}}} log\left( {1 + \mathop \sum \limits_{{i \in \overline{\boldsymbol{\varLambda }}}} \left| {h_{i,j} } \right|^{2} } \right)}}_{{\mathop \sum \limits_{{j \in \left\{ {s,\varLambda } \right\}}} C_{SIMO} \left( {j;\overline{\boldsymbol{\varLambda }}} \right)}} + \underbrace {{log\left( {1 + \mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left| {h_{d,j} } \right|^{2} } \right)}}_{{C_{MISO} \left( {\left\{ {s,{\boldsymbol{\varLambda}}} \right\};d} \right)}}} \right) \\ \end{aligned}$$
(40)

then the min-cut capacity bound is increased. This shows that as long as the min-cut capacity bound is concerned, allowing the relays to communicate to each other pays off the extra channel uses for high SNR regime if Eq. (40) holds.

3.6 Lower bound

A lower bound is straightforwardly obtained by the best link in each transmission of the relay min-cut capacity bound. So, for the low SNR regime, replacing the sum operation by a max operation in the min-cut capacity bound in (23) yields the lower bound in (41). In other words, (41) is a lower bound in the low SNR regime simply because it is a subset of the min-cut capacity bound itself.

$$\overline{C} \ge \frac{1}{L}\min \left[ {SNR\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} \left( {\max \left\{ {\left| {h_{i,j} } \right|^{2} } \right\}_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} } \right)} \right]$$
(41)

Similarly, for the high SNR regime, replacing the sum operation by a max operation in the min-cut capacity bound in (37) yields the lower bound in (42).

$$\overline{C} \ge \frac{1}{L}\log \left( {SNR\left[ {\mathop \sum \limits_{{j \in \left\{ {s,{\boldsymbol{\varLambda}}} \right\}}} {\text{max}}\left\{ {\left| {h_{i,j} } \right|^{2} } \right\}_{{i \in \left\{ {\overline{\boldsymbol{\varLambda }},d} \right\}}} } \right]} \right)$$
(42)

4 Simulation results

The proposed method can be applied to any Gaussian N-relay network where the number of relays N is arbitrary. In what follows, without loss of generality and for the sake of brevity, we examine two networks with 3 relays (in Fig. 5) and 20 relays (in Fig. 12) in Example 1 and 2, respectively. Furthermore, without loss of generality, in both Example 1 and 2 below, we model the channel gains as in e.g. [36, 37] where the attenuation factor is 3, the log-normally distributed slow fading is generated according to the model in [36], and the lognormal variance is 6 dB. The transmit powers vary from 1 mW to 1 W. A unit variance Gaussian noise is added to the received signal at each node.

Fig. 5
figure 5

The Gaussian 3-relay general network example (N = 3)

Full size image

The min-cut capacity bound of the proposed method is verified by the cut-set bounds found by the spectral clustering and using (37) (which was obtained by Eqs. (32)–(33)). For the spectral clustering formulation as applied to the channel allocation problem, see e.g. [38, 39, 43]. Let’s define a discrete-value vector \({\varvec{x}}={\left[{x}_{1} \cdots {x}_{N}\right]}^{T}\) such that

$$x_{i} = \left\{ {\begin{array}{*{20}c} { - 1/2,\quad {\text{if vector }}i{\text{ in set \{ }}s,\varLambda \} } \\ { + 1/2,\quad {\text{if vector }}j{\text{ in set \{ }}\overline{\boldsymbol{\varLambda }},d\} } \\ \end{array} } \right.,\quad i = 1,2, \ldots N.$$

Because \({{\varvec{x}}}^{T}{\varvec{L}}{\varvec{x}} \, = \, {\sum }_{i=1}^{N} {\sum }_{j=1}^{N}{\left|{h}_{i,j}\right|}^{2}{\left({x}_{i}-{x}_{j}\right)}^{2}\), (see e.g. [40,41,42], for details)

$${\text{minCut}}_{{C_{1} ,...,C_{L} }} \left\{ {{\varvec{A}}_{g} } \right\}{ = }\min \left\{ {{\varvec{x}}^{T} {\varvec{Lx}}} \right\}$$
(43)

Relaxing the optimization in (43) such that \({\varvec{x}}\in {\mathfrak{R}}^{N\times 1}\) (instead of being integers), it’s well-known that the optimum solution which maximizes \({{\varvec{h}}}^{T}{\varvec{L}}{\varvec{h}}\) with unit norm constraint is equal to

$${\varvec{x}}^{opt} { } = sign\left( {{\varvec{e}}_{min} } \right)$$
(44)

where L is the Laplacian matrix and \({{\varvec{e}}}_{min}\) is its 2nd minimum eigenvector because the minimum eigenvector gives a trivial solution which is not practical (for details and for further information and references see e.g., [40,41,42]).

Example 1

A 3-Relay network is represented by the following squared channel gain matrix \({{\varvec{A}}}_{g}\) as follows

$${\varvec{A}}_{g}^{3-\mathit{Re}lay}={\left[\begin{array}{c} \, \, 0 \, \, \, \, \, \, {\left|{h}_{1s}\right|}^{2} {\left|{h}_{2s}\right|}^{2} \, \, \, {\left|{h}_{3s}\right|}^{2} \, \, {\left|{h}_{ds}\right|}^{2}\\ {\left|{h}_{1s}\right|}^{2} \, \, \, \, 0 \, \, \, \, \, {\left|{h}_{12}\right|}^{2} \, \, \, {\left|{h}_{13}\right|}^{2} \, \, \, {\left|{h}_{d1}\right|}^{2}\\ \cdots \\ \cdots \\ {\left|{h}_{ds}\right|}^{2} \, \, {\left|{h}_{d1}\right|}^{2} \, \, {\left|{h}_{d2}\right|}^{2} \, \, {\left|{h}_{d3}\right|}^{2} \, \, \, \, 0\end{array}\right]}_{5\times 5}$$
(45)

In order to give an insight into how min-cut capacity bounds change with respect to relay locations, we examine three cases in Figs. 6a, 7a and 8a, which represents the scenario where the relay locations are relatively closer to each other in the middle, the scenario where relay locations are slightly closer to the source and the scenario where relay locations are slightly closer to the destination, respectively. The proposed modified-GADIA (in Table 2) yields source s and relay 3 in one set (shown as yellow diamonds in Fig. 5) and relays 1 and 2 and destination in the other set (shown as red circles in Fig. 5). This means \({\boldsymbol{\varLambda}}= \left\{ 3 \right\}\), and \(\overline{\boldsymbol{\varLambda }} = \left\{ {1, 2} \right\}\) (thus \({N}_{\varLambda }=1\) and\({N}_{\overline{\varLambda } }=2\)). So, we have 3 channel uses (i.e.,\(L=3\)) because there are two SIMO channels from (34) and one MISO channel in Fig. 5.

Fig. 6
figure 6

Case 1: a Relay locations and the final modified-GADIA solution, b evolution of the modified GADIA for the case when transmit power is 1 W, c evolution of the cut when transmit power is 1 W, and d the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 100 mW to 1 W

Full size image
Fig. 7
figure 7

Case 2: a Relay locations and the final modified-GADIA solution, b evolution of the modified GADIA for the case when transmit power is 1 W, c evolution of the cut when transmit power is 1 W, and d the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 100 mW to 1 W

Full size image
Fig. 8
figure 8

Case 3: a Relay locations and the final modified-GADIA solution, b evolution of the modified GADIA for the case when transmit power is 1 W, c evolution of the cut when transmit power is 1 W, and d the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 100 mW to 1 W

Full size image

For the relay locations shown in Fig. 6a, the total interference in the relay network (i.e., \(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\) in (6)), the cut of interference matrix (i.e., \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) in (13)), and the min-cut capacity bounds of the modified-GADIA solution are shown in Fig. 6b–d, respectively, in the high SNR regime. The results of the other two cases (called case 2 and 3) with different relay locations are shown in Figs. 7 and 8. In order to examine if allowing the relays to communicate to each other pays off the extra channel uses or not, we define a relative increase in the min-cut capacity bound with respect to that of the diamond relay network:\(gain\%=\frac{\left({{mincutCapa}_{general}-mincutCapa}_{diamond}\right)}{{mincutCapa}_{diamond}}\times 100\%.\) These gains are shown in Fig. 9 for cases 1, 2, and 3. As seen from Fig. 9, the percentage gains for cases 1, 2 and 3 are positive, varying between + 4 and + 18% depending on the transmit powers (SNRs) and relay locations.

Fig. 9
figure 9

Relative increase in min-cut capacity upper bound (UB) in the high SNR regime for the cases 1, 2 and 3

Full size image

In low-SNR regime, for the relay locations shown in Figs. 6a, 7a and 8a, the cut of interference matrix (i.e., \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) in (13)), and the min-cut capacity bounds of the modified-GADIA solution are shown in Fig. 10a–c respectively. The relative min-cut capacity gains are shown in Fig. 11 for cases 1, 2, and 3 for low SNR. As seen from Fig. 11, the percentage gains for the cases 1, 2 and 3 are positive, varying between + 13% and + 160% depending on the transmit powers (SNRs) and relay locations. Figures 6b, 7b and 8b confirm that the proposed modified GADIA fully loads the relay network by strictly increasing the total network interference so that the min-cut of the relay network is found in a distributed fashion. Figures 6c, 7c, 8c and 10a confirm that the cut of the interference matrix is minimized by the proposed modified simple GADIA in Table 2. In short, all the results (min-cut capacities, modified-GADIA based min-cut capacity bounds, modified simple GADIA evolution, total interference evolution in the relay network, etc.) in Figs. 6, 7, 8, 10 and 11 confirm the findings in Sect. 3.

Fig. 10
figure 10

In the low SNR regime, the cut evolution of the relay network by the modified GADIA for the case when transmit power is 1 mW, and the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 0.1 to 1 mW: a case 1, b case 2 and c case3

Full size image
Fig. 11
figure 11

Relative increase in min-cut capacity upper bound (UB) in the low SNR regime for the cases 1, 2 and 3

Full size image

Example 2

In this example, we increase the number of relays to 20 as seen in Fig. 12(a). For the relay locations shown in Fig. 12a, the total interference in the relay network (i.e., \(I_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{tot} \left( t \right)\) in (6)), the cut of interference matrix (i.e., \(J_{{\overline{\boldsymbol{\varLambda }},{\boldsymbol{\varLambda}}}}^{{}} \left( t \right)\) in (13)), and the min-cut capacity bounds of the modified-GADIA solution are shown in Fig. 12b–d, respectively, in the high SNR regime. The results for low SNR case are presented in Fig. 13. All the results (min-cut capacities, modified-GADIA based min-cut capacity bounds, modified simple GADIA evolution, total interference evolution in the relay network, etc.) in Figs. 12 and 13 confirm that the upper bound in (37) (which is obtained by using Eqs. (32)–(33)) is tight to the min-cut capacity bound and confirm the findings in Sect. 3. Furthermore, we verify the modified simple GADIA based solution with the spectral clustering based solution. The cut bounds obtained by the spectral clustering together with Eq. (37) are presented in Fig. 14. Comparing Fig. 12d and Fig. 14(b), the capacity bounds found by the proposed method are comparable to those of the spectral clustering based capacity bounds obtained by Eq. (37), which verifies the proposed solution.

Fig. 12
figure 12

a Example 2: a Relay locations and the modified-GADIA cluster solution, b evolution of the modified GADIA for the case when transmit power is 1 W, c evolution of the cut when transmit power is 1 W, and d the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 100 mW to 1 W

Full size image
Fig. 13
figure 13

a Case 5: In the low SNR regime, a the cut evolution of the relay network by the modified GADIA for the case when transmit power is 10 mW, and b the min-cut capacity bounds and the upper bound of the relay network as transmit power increases from 1 to 10 mW

Full size image
Fig. 14
figure 14

a Relay locations and the spectral clustering solution and b the cut-set capacity bound and its upper bound of the relay network obtained by the spectral clustering together with (37) as transmit power increases from 100 mW to 1 W

Full size image

5 Conclusions

In this paper, we present a Gaussian N-relay general network by allowing relays to communicate to each other and allowing a direct channel between source and destination in the standard diamond network in [24] at the cost of extra channel uses. The standard N-Relay diamond network [24] is a special case of the presented general N-Relay network. Our investigations yield various novel results some of which are as follows: We

  1. (i)

    propose a modified simple GADIA-based algorithm to find the min-cut capacity upper bound of the Gaussian N-relay network. The proposed modified GADIA-based simple algorithm enables the N-relay general network to determine the relay clusters in a distributed manner.

  2. (ii)

    present a capacity upper bound and a lower bound to its min-cut capacity bound using the modified simple GADIA algorithm. The proposed upper bound is relatively tight to the min-cut capacity bound.

  3. (iii)

    show that the modified GADIA-based upper bounds give an insight into whether allowing the relays to communicate to each other pays off the extra channel uses or not in the general relay network.

  4. (iv)

    verify the proposed capacity bound by comparing the capacity cut-set bounds found by the spectral clustering.

These results also highlight the importance of unleashing the interference avoidance theory for addressing the challenging wireless relay networks capacity problems.

In this paper we focus only on the min-cut capacity upper bounds of the relay networks, and thus we do not consider any particular relay transmission schemes (such as amplitude-and-forward relaying, compute-and-forward, etc.). To examine and design various relay transmission schemes for the Gaussian general N-relay networks would be an interesting future research subject.