Abstract
Recently, the photonics-radar technology comes out as an attractive candidate in the arena of smart autonomous transportation, surveillance, and navigation-related applications owing to provide wide-spectra to attain improved and precise radar-resolutions. On the other hand, microwave radars, due to limited bandwidth, are incapable of coping with the demands of next-generation radar technology. Moreover, the atmospheric fluctuations become more prominent at higher frequencies and affect the radar’s performance significantly. Subsequently, the authors develop a 2 × 2 multi-input multi-output (MIMO) employed linear frequency-modulated continuous-wave coherent photonic-radar system (MIMO-Co-PHRAD) using OptiSystem™ and MATLAB™ to attain a prolonged detection-range with an enhanced visibility. The developed MIMO-Co-PHRAD is investigated with heterodyne- and homodyne-detection approaches under weak-to-strong regimes of the atmospheric fluctuations like Rain and Fog. A comparison is also drawn for both the demonstrated MIMO-equipped laser-driven coherent photonic-radar systems. The performance of both the developed MIMO-Co-PHRAD systems is evaluated by measuring the intensity of reflected-echoes, signal-to-noise ratio, and range-Doppler patterns. A contrast with the single-input single-output coherent photonic-radar (SISO-Co-PHRAD) is also established to validate the robustness of the demonstrated MIMO-Co-PHRAD.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to the latest World Health Organization (WHO) report, about 1.24 million people around the world lost their lives, and ≈ 20–50 million people survive critical damages due to road accidents [1]. Therefore, the autonomous vehicle (AV)-related industries are employing their self-driving vehicles with Advanced Driver Assistance Systems (DAS), including Automotive Collision-Avoidance System (ACAS), Lane Departure Warning System (LDWS), and Brake Assistance System (BAS) [2]. However, the limited range-detection with marginal resolutions provided by the available surveillance and navigation systems makes them comparatively inappropriate for the intelligent automotive industry [3, 4]. Additionally, the state-of-the-art AV-related industries demand high range- and imagery-resolution of the illuminated targets to identify and characterize them with high accuracy. As most of the driving-functions of the self-driving vehicles depend upon the incorporated radar system, the radar needs to be robust enough to provide an accurate range-detection over an extended visibility range with minimal power requirements (\(\le\) 20 W) to avoid any road-hazard [5]. Moreover, the existing microwave radar systems provide marginal detection-range and range-resolution due to limited bandwidth [6]. Therefore, for the last few years, the radar manufacturers have moved towards the 77 GHz frequency band as it offers higher bandwidth (≈ 4 GHz) in contrast to the 24 GHz band (≈ 200 MHz). This wide-bandwidth increases the range- and velocity-resolution along with imagery resolution to identify the closely spaced targets and improves the radar-accuracy [7, 8]. However, the propagation characteristics of the radar signals, especially in the 77 GHz frequency-band experience a significant attenuation [9] when exposed to severe atmospheric situations. Alternatively, the linear frequency-modulated continuous-wave photonic-radar upturns significantly and is growing in intelligent autonomous transportation-related industries rapidly [10,11,12].
The author’s recent work also claims a significant influence of rain, fog, and haze over the coherent and non-coherent configured PHRAD system [13]. However, this work is only demonstrated for a single immobile target. This work is extended further to improve the detection-range in the presence of atmospheric variations by incorporating the spatial-diversity technique to realize a MIMO-Co-PHRAD system, considering immobile and mobile targets. As the 77–81 GHz frequency band offers twenty-time better range-resolution and three-time better velocity-resolution with improved accuracy as compared to the 24–27 GHz frequency band. Subsequently, MIMO-Co-PHRAD is developed at 77 GHz in this work by establishing several traffic-and weathers-scenarios, including several environmental factors (fog and rain) at different severity levels. This work is further extended by modeling a real-time traffic scenario consisting of three automotive targets, including Car, Truck, and Bike, traveling at different speeds before a photonic-radar-equipped vehicle at different distances. The photonic-radar-equipped vehicle is modeled at 100 km/h, assuming all the target-objects are moving towards it. The demonstrated LFMCW-PHRAD computes the target-range and velocity measurements simultaneously for the defined multiple automotive targets. Furthermore, a comparison of the demonstrated MIMO-Co-PHRAD is also established with the SISO-Co-PHRAD to validate its robustness.
The demonstrated MIMO-Co-PHRAD is developed via co-simulation of a well-known photonic software, i.e. OptiSystem™, and the mathematical programming platform, i.e. MATLAB™. In this work, both the demonstrated coherent configured PHRAD systems are modeled in OptiSystem™ photonic-module, while the narrowband LOS channel, target model, and traffic-scenario are developed in the MATLAB™ environment. OptiSystem™ software incorporates a MATLAB component tool that can integrate several modules of MATLAB™ software to design different components or models or systems. Accordingly, the modeled LOS link and target scenario are integrated using this MATLAB component-tool in the photonic environment of the OptiSystem™ to demonstrate the photonic-radar. For making the overall scenario simple, a static target is developed initially in this work, which is further extended to track three different mobile targets in a traffic scenario, modeled using MATLAB™.
This work is presented in six different sections. Section 1 discusses the current developments of photonic-radar and its challenges with the highlights of the demonstrated radar-system. Section 2 discusses the earlier work of MIMO-Co-PHRAD reported in the last few years. Sections 3 and 4 describes the modeling of the MIMO-Co-PHRAD system and the free-space channel. Section 5 discusses the results and discussions of the demonstrated photonic-radar systems considering several traffic-and weather-scenarios. A conclusion based upon the observations is drawn in Sect. 6.
2 Related work
Generally, the laser-driven radar modulates the linear frequency-modulated (LFM) radio-frequency signals using an external modulator to attain spectrally broadened signals. These optical treated pulses are transmitted over the free space via a beam-collimator module towards the illuminated-targets. The beating of target-echoes using photodetector with a suitable detection approach needs additional attention to receive the weakest echo signal with low phase-fluctuations. Due to a high receiver-sensitivity and low phase-noise, the coherent detection outperforms contrast to the non-coherent detection configuration but at the cost of system-complexity [13, 14]. The coherent detection can be implemented in two configurations, i.e. heterodyne-and homodyne mixing, as the latter is more vulnerable to the phase-noise of the optical-carrier. An electro-optic modulator is mostly preferred for coherent heterodyne photonic-radar to attain unprecedented range-resolution [8, 15].
Some recent work has been carried out to measure the impact of environmental factors over the radar performance in RF-and optical-domain. The atmospheric absorption of light pulses at 1550 nm due to CO2 and water-molecules is demonstrated and reported a significant degradation of radar’s performance [16] with limited detection-range. The effect of dust, smoke [17], and gases [18] over the detection-range of laser-driven radar is also observed recently. Furthermore, the signal-fading due to rain, fog, and snow during the propagation of light-treated radar signals cannot be ignored [19,20,21], which validates the influence of atmospheric fluctuations. However, these works are either investigated for single immobile targets or in simple traffic scenarios, considering the impact of individual environmental factors. The situation becomes more complicated under complex traffic-and weather-situations, especially in highly dense traffic-scenes and industrial-dominant areas. For achieving high azimuth-resolution, an accurate direction of arrival (DOA), and multiple target tracking, the photonics radar incorporated with the radar-array technology is an attractive candidate. Recently, a multiple-input-multiple-output (MIMO) radar is considered a promising radar-array, including many comparable transceiver-arrays with minimum hardware requirements. Due to its orthogonal property between different channels, a MIMO radar has the flexibility to realize multiple beamforming, DOA estimation, multiple target tracking, and 2D/3D imaging [22,23,24,25]. Besides, a MIMO radar can achieve a precise target positioning and parameter estimation [26, 27]. A photonics-based 2 × 2 MIMO radar is experimentally demonstrated to estimate the DOA and target positioning [28, 29]. In these approaches, the optically widened radar signals are reconverted into RF signals at the transmitter site and then transmitted towards the targets wirelessly. Alternatively, light-treated LFM radar signals are sent directly towards the targets in the optical domain as light pulses experience low attenuation due to atmospheric variations and safe to the human-eyes as well [8, 13, 15]. However, the MIMO-equipped photonic-radar in optical domain has not been reported comprehensively so far, especially under several weather situations, and is at its initial phases of development.
3 System description
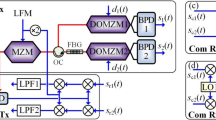
The demonstrated MIMO-Co-PHRAD is employed in heterodyne- and homodyne-mixing configurations using linear frequency-modulated continuous-wave (LFMCW) technique as the automotive radars prefer LFMCW technology due to its compact size and economical installation with low power-needs [10]. Accordingly, for realizing MIMO-Co-PHRAD, an LFM is generated at \({\varvec{f}}_{{\varvec{c}}} =\) 77 GHz with sweep-bandwidth, \({\varvec{B}}_{{{\varvec{sweep}}}}\) in both the coherent configurations, as shown in Fig. 1. If R is the target-range and \({\varvec{T}}_{{\varvec{m}}}\) is sweep-time, then the range-frequency, \({\varvec{f}}_{{\varvec{r}}}\) is calculated [8, 13, 15] as
Further, the LFM signal is modulated over a continuous-wave (CW) laser of 1550 nm with an optical power of 16 dBm and linewidth of 100 kHz using DAMZM modulator. DAMZM is biased at the null transmission-point to attain coherent detection. The suppression of higher-order sidebands is achieved by controlling the bias-voltages of the optical modulator. Accordingly, the switching-and bias-voltage is set to 4 V and – 4 V respectively of the modulator in this work. Moreover, the bias-1 of 2 V and bias-2 of − 2 V are applied to arm-1 and arm-2 of the modulator, respectively.
For MIMO-incorporated coherent-configuration with heterodyning mixing, one part of the generated optical signal is split into two different orthogonal signals after optical modulation and applied to two telescopic lenses, i.e. Tx1 and Tx2 with an aperture diameter of 5 cm each as shown in Fig. 1. Generally, if M, N are the independent orthogonal transmitters and receivers, respectively, then MN be the return-routes from the kth target. Therefore, the generic received signal is computed as [26, 30]
where \(\alpha\) is the complex amplitude of the kth return signal from a target located at an angle \(\theta_{k}\), \(S_{m}\) is the baseband samples of the mth transmitted signal, \(\tau_{mn} \left( {\theta_{k} } \right)\) is the total phase delay between the mth transmitting element, the kth target, and the nth receiver, \(\omega_{c}\) is the carrier frequency, n is the time index. To develop a model of 2 × 2 MIMO-Co-PHRAD, M = N = 2 are taken in this work. These orthogonal signals are transmitted over the free-space channel towards the aiming targets. The reflected echoes from the illuminated target are captured by the receiving telescopic lenses, i.e. Rx1 and Rx2 of an aperture diameter of 15 cm each.
For realizing MIMO-Co-PHRAD with heterodyne-mixing, all the captured echoes by each receiving optical lens are combined by an optical combiner to retrieve a single echo. The detected echo-signal is mixed with the same laser-carrier source used as an input source of light-carrier (CWL) to attain heterodyning-mixing as shown in Fig. 1(a). These optically mixed signals are applied to a balanced photodetector module employed with two PIN diodes in parallel-configuration to accomplish the balance-detection. Each PIN photodetector is sampled at 4 GHz. The ASE-ASE noise, thermal noise, and shot-noise are included for the detection-measurements.
After optical-to-electrical conversion, the de-chirp signal is amplified, filtered out, and beat at FM carrier-frequency to recover the beat signal as [31,32,33,34]
For MIMO-Co-PHRAD with homodyne mixing, the modulated LFM signal is transmitted over the free-space channel towards the aiming target-objects under observation using the beam collimator module in the same way as described in the case of heterodyne mixing. After combining all the echoes captured by the receiving telescopic lenses, the collected echoes are mixed with the optically modulated radar signals using an optical mixer, as shown in Fig. 1(b). The optically mixed de-chirp-signals are reconverted into electrical signals using a balanced photodetector module. The down-converted electrical signals are passed through an LPF after proper electric amplification to recover the beat-signal as [34, 35]
The retrieved beat-signals for both the demonstrated PHRAD system are then analyzed with the help of an RF spectrum analyzer of resolution 1 MHz. Where \(P_{r}\) is the received power of the captured echo, \(P_{t}\) is the power of the optical pulse after optical amplification, m is modulation index = \(\frac{{\pi . A_{0} }}{{V_{\pi dc} }} \ll 1 \), \(B_{sweep}\) = 300 MHz, \(A_{lo} \) = optical-carrier amplitude, \(A_{0} =\) RF-carrier amplitude, Vπdc = bias-voltage of the modulator, \(R_{PD}\) = Responsivity of each photo-detector (PIN) = 0.8 AW−1, \(\tau\) is propagation delay.
4 Channel-modeling
The range-visibility < 100 m is considered as a zero-visibility in the AV-related applications and thus, enhances the possibilities of unfortunate road-hazards. Moreover, the atmospheric fluctuations due to fog, rain, and haze, and snow makes the situation more challenging for self-driving vehicles. It has been reported that fog and rain are the main environmental factors that deteriorate the radar performance severely at higher frequencies, i.e. in the mmW band. Subsequently, in this section, a free-space channel model is developed using the phased-array system toolbox of MATLAB™, including the influence of fog and rain at different severity levels. Therefore, for both the demonstrated PHRAD systems, an investigation is carried out in the presence of rain varying from the weak-to-severe regime. Specifically, the rain attenuation, \(A_{att} \left( {\text{dB/km}} \right)\) at rainfall rate, \(R_{0}\)(mm/h) is calculated [36, 37] as
where \(k \) and \(\alpha\) are power-law parameters depending upon the used mmW-band, raindrop-size, and temperature. By computing the values of power-law parameters as per the Marshall–Palmer distribution [37], the \(A_{att} \left( {\text{dB/km}} \right)\) is measured as ≈ 24 dB/km for heavy-rain at \(R_{0}\) = 50 mm/h, ≈ 14.25 dB/km for mild-rain at \(R_{0}\) = 25 mm/h, and ≈ 4 dB/km for low-rain at \(R_{0}\) = 5 mm/h respectively.
Fog is another dominant degrading environmental factor parameter that deteriorates the visibility range due to its dependence on water–vapor density and particle-size distribution [38]. The specific attenuation due to fog computed by an empirical model for Mie scattering is given [39] as
where V (km) = visibility range, \(\lambda \left( {{\text{nm}}} \right)\) = Laser’s operating wavelength, and p is the size distribution-coefficient of scattering, which can be measured by the Kim model [40] as
According to the Kim model, the specific attenuation for heavy-, mild-, low-fog scenarios are calculated as 84.90 dB/Km, 33.96 dB/Km, and 14.55 dB/Km respectively [37, 38]. Further, all the measurements are carried out by considering the weak-atmospheric turbulence fluctuations with a refraction-index structure of air of 10–17 throughout the work. The receiver threshold is set as 16.5 dB, measured according to Neyman–Pearson (NP) decision-rule [20].
5 Results and discussions
This section presents a comprehensive discussion on the outcomes computed for the established model of 2 2 MIMO-Co-PHRAD by measuring the captured echoes reflected from the target. The performance of both the demonstrated MIMO-Co-PHRAD is measured in terms of signal-to-noise ratio by considering the weak-to-strong atmospheric regimes of rain and fog to comprehend the influence of the weather fluctuations. A comparative investigation of the demonstrated MIMO-Co-PHRAD and SISO-Co-PHRAD is also carried out to determine the impact of the spatial-diversity over radar-performance. The work is further extended to test the demonstrated MIMO-Co-PHRAD in a developed traffic-scenario consisting of three different target-objects.
The observations for the demonstrated MIMO-Co-PHRAD in contrast with SISO-Co-PHRAD under clear-weather scenarios are shown in Fig. 2. It is observed that MIMO-Co-PHRAD captures the strong reflected-echoes in both the established coherent configurations, in contrast to the SISO-PHRAD, as shown in Fig. 2. This is due to the introduction of multiple routes by the spatial-diversity technique of the MIMO technology, thus, resulting in high throughput and signal-to-noise ratio. The results show that heterodyne mixing attains strong return-signals in contrast with homodyne mixing due to a high frequency-offset, caused by LO leakages. Subsequently, the demonstrated work is examined further employed with heterodyne mixing to measure the influence of atmospheric fluctuations. The outcomes show that fog, at the mild-to-heavy severity-level, influences the detection-range significantly by imposing an apparent power-loss of the reflected-echoes. For SISO-Co-PHRAD with heterodyne mixing, the visibility-range of ≈ 300 m and ≈ 500 m under heavy-fog and mild-fog scenarios is attained, respectively, as shown in Figs. 3(a, c) and 4(a). it is also apparent from the attained observations that heavy-rain also limits the detection-range but, its impact is observed comparatively less in contrast to the mild-to-heavy fog-scenario. The detection-range under the heavy-rain scenario is measured as ≈ 800 m for SISO-Co-PHRAD. However, the weak atmospheric regimes show marginal impact, cannot be ignored in complex real-time traffic-scenarios consisting of high target-density or in industrial areas due to the presence of high-density air-pollutants. For MIMO-Co-PHRAD with heterodyne mixing, a prolonged detection-range is attained in contrast to SISO-Co-PHRAD under the influence of all the environmental factors as shown in Figs. 3(b) and 4(b). The visibility-range of ≈ 470 m, ≈ 960 m, ≈ 1160 m is measured under heavy-fog, mild-fog, and heavy-rain scenarios, respectively. This shows the impact of the spatial diversity over the performance of the LFMCW-PHRAD under atmospheric variations, which can be utilized to compensate for the signal-degradation introduced by fog, and rain factors. Alternatively, the detection-range significantly deteriorates in some other complex and environmental situations, including the co-existence of smoke, air-pollutants, and fog especially, in a smoggy-situation, in winter season in industry-dominated areas. However, the smoke, other gasses, and dust particles are not included while carrying out the measurements in this work.
It is worth mentioning here that it is difficult to identify the illuminated targets under adverse weather-and traffic-situations, which can be done by measuring the intensity of the echoes that depend upon the reflectance characteristics of the target-materials. The reflectance characteristics of a particular target can be measured by computing the Bidirectional reflectance distribution function using the Torrance–Sparrow model to retrieve its dimensions [8]. Moreover, with an improved signal-to-noise ratio due to the implementation of MIMO technology, as observed in the demonstrated work, the photonic-radar has high possibilities to realize state-of-the-art self-driving vehicles to work satisfactorily under adverse weather- and traffic-situations.
This work is further extended by developing a real-time traffic scenario, including three mobile-targets (Car, Truck, and Bike) under the influence of fog and rain. The target-vehicles are moving at 96 km/h (Car), 90 km/h (Truck), 70 km/h (Bike) at a distance of 400 m, 450 m, and 250 m, respectively from a radar-equipped vehicle, which is moving at 100 km/h. Figure 5 shows the range-Doppler measurements showing the detection of the targets with their exact location. The power-spectrum density (PDF) are measured as ≈ − 98.063 dBm/Hz, ≈ − 93.127 dBm/Hz, ≈ − 86.516 dBm/Hz for Car, Truck, and Bike, respectively, under the heavy-rain scenario. Under heavy-fog scenario, it is measured as ≈ − 116.166 dBm/Hz, ≈ − 111.721 dBm/Hz, ≈ − 101.118 dBm/Hz. A difference in PSD measurements for the Car, Truck, and Bike is also observed, which is due to the different radar-cross section of the modeled targets. An improvement in PSD measurements is recorded as 15.5%, 16.2%, 17.3% for cars, trucks, and Bikes under both the examined environmental factors, which reveals out that fog is a more detrimental factor than that of rain. The results show the concurrent measurements of range and velocity of the targets unambiguously and successfully for the developed MIMO-Co-PHRAD under the influence of fog and rain. Moreover, the demonstrated MIMO-Co-PHRAD shows a marginal Total Harmonic distortion (THD), high Signal-to-Noise and Distortion Ratio (SINAD), and small Spurious-free dynamic (SFDR) ratio at the receiving end.
The demonstrated work is limited to a simulative environment using the co-simulation of OptiSystem™ and MATLAB™. Moreover, the authors believe that there may be some variations in real-time experiments in contrast to the numerical simulation measurements. However, the demonstrated work will be helpful for the researchers in developing MIMO-employed laser-driven radar systems experimentally to realize the state-of-the-art self-driving vehicles and other surveillance-related applications. Therefore, we believe that the extension of this work can be accomplished in the future to perform experimental and field-trials-based measurements.
Secondly, though the traffic-and atmospheric-conditions are unpredictable, the MIMO-Co-PHRAD has the potential to detect the aiming targets simultaneously with high precision [22,23,24,25,26,27,28,29]. However, there are possibilities to optimize the demonstrated system keeping in mind the unpredictable traffic-and atmospheric-fluctuations. So, an adaptive photonic-radar system is realizable by incorporating a suitable optimization technique. Moreover, Due to an exponential increase in system-complexity and undesirable delay at the receiving end with an increase in the number of transmitting lenses [41], the authors use 2 × 2 beam collimator lenses to keep the system-complexity minimum. Moreover, besides numerous assets of MIMO employed radar systems, there are some challenges of high implementation cost with multiple transmission and reception of radio-frequency channels causes expensive digital signal processing (DSP) modules which can be compensated using the Realistic Sparse Fourier transform (RSFT) and achieve reduced DSP complexity [42]. Therefore, this work may be extended to realize a MIMO-RSFT incorporated photonic-radar system.
6 Conclusion
This work demonstrated an LFMCW-driven MIMO-Co-PHRAD radar in the presence of weak-to-strong atmospheric variations using two different coherent detection configurations. This work is further extended to measure the range and speed of three automotive mobile targets concurrently in a modeled traffic-scenario under the individual influence of the fog and rain. The outcomes validate that by incorporating the spatial-diversity, an extended target-range can be accomplished with MIMO-Co-PHRAD in contrast with the SISO-Co-PHRAD. The observations show that spatial-diversity can play a significant role in attaining better radar-performance by reducing the impact of environmental fluctuations for AV-related applications. Our results achieve an improvement in detection-range of ≈ 56%, ≈ 92%, ≈ 45% under heavy-fog, mild-fog, and heavy-rain respectively for MIMO-Co-PHRAD in contrast with the SISO-Co-PHRAD. The demonstrated MIMO-Co-PHRAD can be extended in future work to carry out experimental demonstrations in more complex traffic-scenarios under the influence of adverse atmospheric fluctuations.
References
Mukhtar, A., Xia, L., & Tang, T. B. (2015). Vehicle detection techniques for collision avoidance systems: A review. IEEE Transactions on Intelligent Transportation Systems, 16(5), 2318–2338. https://doi.org/10.1109/tits.2015.2409109.
Zhou, H., Cao, P., & Chen, S. (2016). A novel waveform design for multi-target detection in automotive FMCW radar. In IEEE radar conference. https://doi.org/https://doi.org/10.1109/radar.2016.7485315
Skog, I., & Handel, P. (2009). In-car positioning and navigation technologies—A survey. IEEE Transactions of Intelligent Transport Systems, 10, 4–21.
Mautz, R. (2008).Combination of indoor and outdoor positioning. In Proceedings of 1st international conference on machine control and guidance (pp. 79–87).
Kutila, M., Pyykönen, P., Ritter, W., Sawade, O., & Schäufele, B. (2016). Automotive photonic-radar sensor development scenarios for harsh weather conditions. In Proceedings of IEEE 19th international conference on intelligent transportation systems (ITSC) (pp. 265–270).
Dudek, M., Nasr, I., Bozsik, G., Hamouda, M., Kissinger, D., & Fischer, G. (2015). System analysis of a phased-array radar applying adaptive beam control for future automotive safety applications. IEEE Transactions on Vehicular Technology, 64(1), 34–47.
Ramasubramanian, K., & Ramaiah, K. (2018). Moving from legacy 24 GHz to state-of-the-art 77-GHz radar. ATZ Elektronik Worldwide, 13, 46–49. https://doi.org/10.1007/s38314-018-0029-6.
Sharma, V., Sergeyev, S., Kumar, L., & Kbashi, H. J. (2020). Range-speed mapping and target-classification measurements of automotive targets using photonic-radar. Optical and Quantum Electronics, 52, 438. https://doi.org/10.1007/s11082-020-02557-5.
ITU-R P.838-3. (2005). Specific attenuation model for rain for use in prediction methods.
Wei, W., Jinsong, D., & Jie, G. (2018). Multi-target-detection method based on variable carrier frequency chirp sequence. Sensors, 18, 3386.
Hu, C., Liu, Y., Meng, H., & Wang, X. (2014). Randomized switched antenna array FMCW radar for automotive applications. IEEE Transactions on Vehicular Technology, 63(8), 3624–3641.
Patole, S. M., Torlak, M., Wang, D., & Ali, M. (2017). Automotive radars: A review of signal processing techniques. IEEE Signal Processing Magazine, 34(2), 22–35.
Sharma, V., & Sergeyev, S. (2020). Range detection assessment of photonic-radar under adverse weather perceptions. Optics Communications, 472, 125891. https://doi.org/10.1016/j.optcom.2020.125891.
Bouteyre, D., Canat, G., Valla, M., Augère, B., Besson, C., Goular, D., Lombard, L., Cariou, J.-P., Durecu, A., Fleury, D., Bricteux, L., Brousmiche, S., Lugan, S., & Macq, B. (2009). Pulsed 1.5 µm lidar for axial aircraft wake vortex detection based on high brightness large-core fiber amplifier. IEEE Journal of Selected Topics of Quantum Electronics, 15, 441–450.
Gao, S., & Hui, R. (2012). Frequency-modulated continuous-wave lidar using I/Q modulator for simplified heterodyne detection. Optics Letters, 37(11), 2022–2024.
ITU-R P.676-11. (2016). Attenuation by atmospheric gases.
Peynot, T., Underwood, J., & Scheding, S. (2009). Towards reliable perception for unmanned ground vehicles in challenging conditions. In Proceedings of IEEE/RSJ international conference on intelligent robots and systems (pp. 1170–1176).
Hasirlioglu, S., Riener, A., Ruber, W., & Wintersberger, P. (2017). Effects of exhaust gases on laser scanner data quality at low ambient temperatures. In Proceedings of IEEE intelligent vehicle symposium (pp. 1708–1713).
Bijelic, M., Gruber, T., & Ritter, W. (2018). A benchmark for photonic-radar sensors in fog: Is detection breaking down? In Proceedings of IEEE intelligent vehicles symposium (IV) (pp. 760–767).
Heinzler, R., Schindler, P., Seekircher, J., Ritter, W., & Stork, W. (2019). Weather influence and classification with automotive lidar sensors. In 2019 IEEE intelligent vehicles symposium (IV) (pp. 1527–1534).
Filgueira, A., González-Jorge, H., Lagüela, S., Díaz-Vilariño, L., & Arias, P. (2017). Quantifying the influence of rain in LiDAR performance. Measurement, 95, 143–148.
Aldayel, O., Monga, V., & Rangaswamy, M. (2017). Tractable transmit MIMO beam pattern design under a constant modulus constraint. IEEE Transactions on Signal Processing, 65(10), 2588–2599.
Ma, C., Yeo, T. S., Zhao, Y., & Feng, J. (2014). MIMO radar 3D imaging based on combined amplitude and total variation cost function with sequential order one negative exponential form. IEEE Transactions on Image Processing, 23(5), 2168–2183.
Yao, T., Zhu, D., Ben, D., & Pan, S. (2015). Distributed MIMO chaotic radar based on wavelength-division multiplexing technology. Optics Letter, 40(8), 1631–1634.
Yang, H., & Chun, J. (2016). An improved algebraic solution for moving target localization in non-coherent MIMO radar systems. IEEE Transactions on Signal Processing, 64(1), 258–270.
Bekkerman, I., & Tabrikian, J. (2006). Target detection and localization using MIMO radars and sonars. IEEE Transactions on Signal Processing, 54(10), 3873–3883.
Li, J., & Stoica, P. (2007). MIMO radar with collocated antennas. IEEE Signal Processing Magazine, 24(5), 106–114.
Zhang, F., Gao, B., & Pan, S. (2018). Photonics-based MIMO radar with high-resolution and fast detection capability. Optics Express, 26, 17529–17540.
Ghelfi, P., Laghezza, F., Scotti, F., Serafino, G., Capria, A., Pinna, S., Onori, D., Porzi, C., Scaffardi, M., Malacarne, A., & Vercesi, V. (2020). A fully photonics-based coherent radar system. Nature, 507, 341–345. https://doi.org/10.1038/nature13078.
Sévigny, P. (2009). MIMO radar: Literature survey of papers between 2003 and September 2008. . DRDC.
Zhou, P., Zhang, F., & Pan, S. (2018). Generation of linear frequency-modulated waveforms by a frequency-sweeping optoelectronic oscillator. Journal of Lightwave Technology, 36(18), 3927–3934.
Varshney, P. K., & Masazade, E. (2014). Academic press library in signal processing.
Agrawal, G. P. (2012). Fiber-optic communication systems. (Vol. 222). Wiley.
Elghandour, A. H., & Ren, C. D. (2013).Modelling and comparative study of various detection techniques for FMCW photonic-radar using optisystem. In Proceedings of SPIE 8905, international symposium on photo-electronic detection and imaging: Laser sensing and imaging.
Elghandour, A., & Dianren, C. (2012). Study on detection techniques of distance and velocity by chirped LIDAR. In 2012 international conference on optoelectronics and microelectronics (pp. 354–358).
Rashidi, F., Jing, H., & Chen, L. (2017). Spectrum slicing WDM for FSO communication systems under the heavy rain weather. Optics Communications, 387, 296–302.
Olsen, R. L., Rogers, D. V., & Hodge, D. B. (1978). The aRb relation in the calculation of rain attenuation. IEEE Transactions on Antennas and Propagation, 26, 318–329.
Gultepe, I., Tardif, R., Michaelides, S. C., Cermak, J., Bott, A., Bendix, J., Müller, M. D., Pagowski, M., Hansen, B., Ellrod, G., & Jacobs, W. (2007). Fog research: A review of past achievements and future perspectives. Pure and Applied Geophysics, 164(6–7), 1121–1159.
Kaushal, H., Jain, V. K., & Kar, S. (2017). Free space optical communication, 1st ed (pp. 41–86). Springer. ISBN 978-81-322-3691-7. https://doi.org/https://doi.org/10.1007/978-81-322-3691-7
Kim, I. I., & Korevaar, E. Availability of Free Space Optics (FSO) and hybrid FSO/RF systems. Light point technical report. www.opticalaccess.com
Sharma, V., Sergeyev, S., & Kaur, J. (2020). Adaptive 2 × 2 MIMO employed wavelet-OFDM-radio over fibre transmission. IEEE Access, 8, 23336–23345. https://doi.org/10.1109/ACCESS.2020.2970085.
Wang, S., Patel, V. M., & Petropulu, A. (2017). MIMO-RSFT radar: A reduced complexity MIMO radar based on the Sparse Fourier Transform. In 2017 IEEE radar conference (RadarConf) (pp. 0885–0890). https://doi.org/https://doi.org/10.1109/RADAR.2017.7944328
Acknowledgements
This work is carried out in Aston Institute of Photonic Technologies, Aston University, Birmingham, UK, and is supported by European Union-sponsored H2020-MSCA-IF-EF-ST project (840267).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sharma, V., Kbashi, H.J. & Sergeyev, S. MIMO-employed coherent photonic-radar (MIMO-Co-PHRAD) for detection and ranging. Wireless Netw 27, 2549–2558 (2021). https://doi.org/10.1007/s11276-021-02605-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-021-02605-2