Full-duplex wireless information and power transfer in two-way relaying networks with self-energy recycling

Abstract

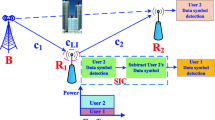
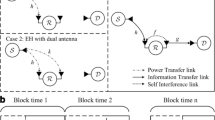
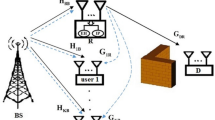
In this paper, we consider full-duplex (FD) two-way relaying networks, where wireless power transfers from hybrid power access-point, H to user and wireless information transmits from user to H via relay. We propose FD-based power splitting (PS) and time-switching (TS) protocols which enables the energy harvesting (EH) and information processing at relay. These protocols overcome the limitation of spectral efficiency and in band self-interference caused by half-duplex relaying and operation of FD respectively. The energy constraint nodes such as relay and user harvest energy from H by radio-frequency signal, where relay also harvests energy by self-energy recycling. The optimal PS ratio and the optimal TS ratio are investigated and expressed in closed-form. With Rayleigh fading channel, we derive the end-to-end ergodic capacity for PS and TS protocols. Numerical results show that our proposed FD-based EH schemes outperform the benchmark schemes significantly. In particular, the PS protocol is superior to TS protocol at high transmit power of H while at low transmit power of H, TS protocol is better than the PS protocol.

Appendices

Appendix 1

1.1 Proof of Theorem 1

In this appendix, we derive the closed-form expression of PS ratio for FD-based EH in two-way AF relaying system. From (19), we can observe that the end-to-end ergodic capacity for PS protocol should be maximized when we maximize the SINR from u-to-H, $\gamma_{uH}^{PS} \left( \alpha \right)$. For maximizing $\gamma_{uH}^{PS} \left( \alpha \right)$, we minimize the denominator of (18). For computing the PS ratio, we follow some important steps which is given below.

Step 1: We consider denominator of (18) that can be written as

$$\tilde{\gamma }\left( \alpha \right) = \frac{{a_{1} }}{{1 - \alpha^{2} }} + \frac{{a_{2} }}{1 + \alpha } + \frac{{a_{3} }}{{\left( {1 - \alpha^{2} } \right)\left( {1 + \alpha } \right)}}$$

(52)

where $a_{1} = \left| {h_{1} } \right|^{2} \sigma_{R}^{2}$, $a_{2} = \xi \left| {h_{2} } \right|^{4} \sigma_{H}^{2}$ and $a_{3} = \frac{{\left( {1 - \xi \left| {h_{R} } \right|^{2} } \right)\sigma_{R}^{2} \sigma_{H}^{2} }}{{\xi P_{H} \left| {h_{1} } \right|^{2} }}$.

Step 2: The derivative of $\tilde{\gamma }\left( \alpha \right)$ with respect to $\alpha$ can be expressed as

$$\frac{{\delta \tilde{\gamma }\left( \alpha \right)}}{\delta \alpha } = \frac{{2a_{1} \alpha }}{{\left( {1 - \alpha^{2} } \right)^{2} }} - \frac{{a_{2} }}{{\left( {1 + \alpha } \right)^{2} }} - \frac{{a_{3} \left( {1 - 2\alpha - 3\alpha^{2} } \right)}}{{\left\{ {\left( {1 - \alpha^{2} } \right)\left( {1 + \alpha } \right)} \right\}^{2} }}$$

(53)

Step 3: We set $\frac{{\delta \tilde{\gamma }\left( \alpha \right)}}{\delta \alpha }$ to be zero and then we obtain polynomial in $\alpha$ as

$$\alpha^{4} - \frac{{2a_{1} }}{{a_{2} }}\alpha^{3} - \left( {2 + \frac{{4a_{1} }}{{a_{2} }} + \frac{{3a_{3} }}{{a_{2} }}} \right)\alpha^{2} - 2\left( {\frac{{a_{1} }}{{a_{2} }} + \frac{{a_{3} }}{{a_{2} }}} \right)\alpha + \left( {1 + \frac{{a_{3} }}{{a_{2} }}} \right) = 0$$

(54)

It is difficult to tractable the closed-form expression of PS ratio,$\alpha$. Note that the term $\frac{{a_{3} }}{{a_{2} }} \propto \frac{1}{{P_{H} }}$. Thus, we consider special case as transmit power of H, $P_{H}$ is very large i.e., $a_{3} \approx 0$. Hence, polynomial of (54) can be rewritten as

$$\alpha^{4} - a\alpha^{3} - 2\left( {1 + a} \right)\alpha^{2} - a\alpha + 1 = 0$$

(55)

where $a = \frac{{2a_{1} }}{{a_{2} }} = \frac{{2\left| {h_{1} } \right|^{2} \sigma_{R}^{2} }}{{\xi \left| {h_{2} } \right|^{4} \sigma_{H}^{2} }}$.

The roots of $\alpha$ can be evaluated with the help of [41, 3.8.3] as

$$\alpha = 1 - \frac{1}{2}\left[ {\sqrt {a\left( {a + 4} \right)} - a} \right]$$

(56)

Step 4: We obtain second derivative of $\tilde{\gamma }\left( \alpha \right)$ with respect to $\alpha$ as

$$\frac{{\partial^{2} \tilde{\gamma }\left( \alpha \right)}}{{\partial \alpha^{2} }} = \frac{{2a_{1} \left( {1 + 3\alpha^{2} } \right)}}{{\left( {1 - \alpha^{2} } \right)^{3} }} + \frac{{2a_{2} }}{{\left( {1 + \alpha } \right)^{3} }} + \frac{{4a_{3} \left( {1 + 4\alpha^{3} + 3\alpha^{4} } \right)}}{{\left\{ {\left( {1 - \alpha^{2} } \right)\left( {1 + \alpha } \right)} \right\}^{3} }}$$

(57)

Since, value of $\alpha$ defines in the range of 0 to 1 i.e., $0 \le \alpha \le 1$. Thus, we observe that the $\frac{{\delta^{2} \tilde{\gamma }\left( \alpha \right)}}{{\delta \alpha^{2} }} \ge 0$. Further, we achieve that the $\tilde{\gamma }\left( \alpha \right)$ is minimum at $\alpha = 1 - \frac{1}{2}\left[ {\sqrt {a\left( {a + 4} \right)} - a} \right]$. The denominator of $\gamma \left( \alpha \right)$ i.e., $\tilde{\gamma }\left( \alpha \right)$ is convex with $\in \left( {0, 1} \right)$. Thereby, SINR from user to H, $\gamma_{uH}^{PS} \left( \alpha \right)$ is concave with $\alpha \in \left( {0, 1} \right)$. Finally, we conclude that the end-to-end capacity from u-to-H for PS protocol achieves maximum at $\alpha = 1 - \frac{1}{2}\left[ {\sqrt {a\left( {a + 4} \right)} - a} \right]$. Thus, this completes the Proof of Theorem 1.

Appendix 2

2.1 Proof of Theorem 2 and Lemma 1

In this section, we investigate the closed-form expression of ergodic capacity from u-to-H for Rayleigh fading.

Proof of Theorem 1

We assume that the fading gains $x = \left| {h_{1} } \right|^{2}$, $y = \left| {h_{2} } \right|^{2}$ and residual self-interference channel gain, $z = \left| {h_{R} } \right|^{2}$ are exponential distributed and followed by Rayleigh fading with means $\mu_{1} = {\mathbb{E}}\left\{ {\left| {h_{1} } \right|^{2} } \right\}$, $\mu_{2} = {\mathbb{E}}\left\{ {\left| {h_{2} } \right|^{2} } \right\}$ and $\mu_{R} = {\mathbb{E}}\left\{ {\left| {h_{R} } \right|^{2} } \right\}$ respectively. The joint probability density function (pdf) of $x$, $y$, and $z$ is defined in [42] as $f_{XYZ} \left( {x, y, z} \right) = \frac{1}{{\mu_{1} \mu_{2} \mu_{R} }}e^{{ - \left( {\frac{x}{{\mu_{1} }} + \frac{y}{{\mu_{2} }} + \frac{z}{{\mu_{R} }}} \right)}}$. Therefore, the ergodic capacity from u-to-H is expressed as

$$C_{E,uH}^{PS} = \frac{1}{2}\iiint {\log_{2} \left( {1 + \gamma_{uH}^{PS} \left( {x,y,z} \right)} \right)}f_{XYZ} \left( {x,y,z} \right)dxdydz$$

(58)

Substituting (17) and $f_{XYZ} \left( {x, y, z} \right)$ in (58), we can write ergodic capacity from u-to-H as

$$\begin{aligned} & C_{E,uH}^{PS} = \frac{1}{{2\mu_{1} \mu_{2} \mu_{R} \ln 2}}\iint {\left\{ {\int\limits_{0}^{\infty } {\ln \left[ {1 + \frac{{A\left( {x,z} \right)y^{2} }}{{B\left( {x,z} \right) + b_{4} xy^{2} }}} \right]e^{{ - \frac{y}{{\mu_{2} }}}} dy} } \right\}e^{{ - \frac{x}{{\mu_{1} }}}} e^{{ - \frac{z}{{\mu_{R} }}}} dxdz} \\ & A\left( {x,z} \right) = \frac{{b_{1} x^{3} }}{{1 - b_{2} z}}\;{\text{and}}\;B\left( {x,z} \right) = b_{3} x^{2} + b_{5} \left( {1 - b_{2} z} \right) \\ \end{aligned}$$

(59)

Note that the set of value, $\left\{ {b_{1} , b_{2} , b_{3} , b_{4} , b_{5} } \right\}$ has been written in (23). We lookup table [43, 3.354.2] and then evaluate ergodic capacity from u-to-H as (22). Thus, this completes the proof of Theorem 2.

Proof of Lemma 1

We assume that the channel gain from H-to-R, $\left| {h_{1} } \right|^{2}$ and residual self-interference channel gain, $\left| {h_{R} } \right|^{2}$ are stationary and channel gain from u-to-R, $\left| {h_{2} } \right|^{2}$ is exponentially distributed and followed by Rayleigh fading. The pdf of function of y defines as, $f_{Y} \left( y \right) = \frac{1}{{\mu_{2} }}e^{{ - \left( {\frac{y}{{\mu_{2} }}} \right)}}$. Thereby, the ergodic capacity from u-to-H is given by

$$C_{E,uH}^{PS} = \frac{1}{2}\int\limits_{0}^{\infty } {\log_{2} \left( {1 + \gamma_{uH}^{PS} \left( y \right)} \right)} f_{Y} \left( y \right)dy$$

(60)

With the help of table in [42, 3.354.2] and (17), we evaluate the ergodic capacity from u-to-H as (24). Thereby, the proof of Lemma 1 is completed.

Appendix 3

3.1 Proof of Theorem 3

In this appendix, we evaluate the closed-form expression of TS ratio for FD-based EH in two-way AF relaying.

Proof of Theorem 3

Substituting (40) into (42), we can express the end-to-end channel capacity for TS protocol as

$$C_{uH}^{TS} = \frac{1}{2}\left( {1 - \delta } \right)\log_{2} \left[ {1 + \frac{{{{\left( {1 + \delta } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \delta } \right)} {\left( {1 - \delta } \right)}}} \right. \kern-0pt} {\left( {1 - \delta } \right)}}}}{{f_{1} \left\{ {f_{2} + f_{3} \frac{1 - \delta }{1 + \delta }} \right\}}}} \right]$$

(61)

Note that the ratio, $\frac{{f_{3} }}{{f_{2} }} \propto \frac{1}{{P_{H} }}$. We assume that the $P_{H} \gg P_{u}^{TS}$. Therefore, $f_{3} \approx 0$. The (61) can be rewritten as

$$C_{uH}^{TS} \left( \delta \right) = \frac{1}{2}\left( {1 - \delta } \right)\log_{2} \left[ {1 + \frac{{\left( {1 + \delta } \right)}}{{f_{0} \left( {1 - \delta } \right)}}} \right]$$

(62)

where $f_{0} = f_{1} f_{2}$. We follow steps to compute the TS ratio which is given below.

Step 1: We derivate (62) with respect to $\delta$ and it can be written as

$$\frac{{\delta C_{uH}^{TS} \left( \delta \right)}}{\delta \delta } = \frac{1}{2\ln 2}\left[ {\frac{2}{{f_{0} \left( {1 - \delta } \right) + \left( {1 + \delta } \right)}} - \log_{2} \left\{ {1 + \frac{{\left( {1 + \delta } \right)}}{{f_{0} \left( {1 - \delta } \right)}}} \right\}} \right]$$

(63)

Step 2: We set derivative in (63) to be zero. We get

$$pe^{p} = \varepsilon$$

(64)

where $\varepsilon = \left( {\frac{1}{{f_{0} }} - 1} \right)e^{ - 1}$ and $p = \frac{{\left( {1 - \delta } \right)\left( {1 - f_{0} } \right)}}{{f_{0} \left( {1 - \delta } \right) + \left( {1 + \delta } \right)}}$.Thus, we obtain TS ratio as (43).

Step 3: The second derivative of (62) can be expressed as

$$\frac{{\partial^{2} C_{uH}^{TS} \left( \delta \right)}}{{\partial \delta^{2} }} = \frac{ - 2}{{\left( {1 - \delta } \right)\left[ {f_{0} \left( {1 - \delta } \right) + \left( {1 + \delta } \right)} \right]^{2} \ln 2}}$$

(65)

From (65), it is clear that the $\frac{{\partial^{2} C_{uH}^{TS} \left( \delta \right)}}{{\partial \delta^{2} }} \le 0$ with $\delta \in \left[ {0, 1} \right]$. Thus, the end-to-end capacity from u-to-H for TS protocol is maximum at $\delta$ that is given in (43). The proof of Theorem 3 is completed.

Appendix 4

4.1 Proof of Theorem 4 and Lemma 2

In this appendix, we investigate the end-to-end ergodic capacity from u-to-H for TS protocol.

Proof of Theorem 4

Similar to “Appendix 2”, we considered gains, $\left\{ {x, y, z} \right\}$ and joint pdf. The end-to-end ergodic capacity from u-to-H with TS protocol for Rayleigh fading is expressed as

$$C_{E,uH}^{TS} = \frac{{\left( {1 - \delta } \right)}}{2}\iiint {\log_{2} \left( {1 + \gamma_{uH}^{TS} \left( {x,y,z} \right)} \right)}f_{XYZ} \left( {x,y,z} \right)dxdydz$$

(66)

By substituting (40) in (66), we can write as

$$\begin{aligned} & C_{E,uH}^{TS} = \frac{{\left( {1 - \delta } \right)}}{{2\mu_{1} \mu_{2} \mu_{R} \ln 2}}\iint {\left\{ {\int\limits_{0}^{\infty } {\ln \left[ {1 + \frac{{B_{0} \left( {x,z} \right)y^{2} }}{{B_{1} \left( {x,z} \right) + k_{2} xy^{2} }}} \right]e^{{ - \frac{y}{{\mu_{2} }}}} dy} } \right\}e^{{ - \frac{x}{{\mu_{1} }}}} e^{{ - \frac{z}{{\mu_{R} }}}} dxdz} \\ & B_{0} \left( {x,z} \right) = \frac{{k_{0} x^{3} }}{1 - \xi z}\;{\text{and}}\;B_{1} \left( {x,z} \right) = k_{1} x^{2} + k_{3} \left( {1 - \xi z} \right) \\ \end{aligned}$$

(67)

The set of value, $\left\{ {k_{0} , k_{1} , k_{2} , k_{3} } \right\}$ has been given in (46). We see [42, 3.354.2] and then compute ergodic capacity from u-to-H as (45). Thereby, the proof of Theorem 4 is completed.

Proof of Lemma 2

For TS protocol, we follow same condition as Lemma 1 and then we obtain end-to-end channel capacity from u-to-H can be written as

$$C_{E,uH}^{TS} = \frac{{\left( {1 - \delta } \right)}}{2}\int\limits_{0}^{\infty } {\log_{2} \left( {1 + \gamma_{uH}^{TS} \left( y \right)} \right)} f_{Y} \left( y \right)dy$$

(68)

With the help of table in [42, 3.354.2] and (40), we evaluate the ergodic capacity from u-to-H for TS protocol as (47). Thus, this completes the proof of Lemma 2.