Abstract
Two radio air interfaces, Evolved-LTE and New Radio, coexist in new 5G systems. New Radio operates in the millimeter band and provides a better bandwidth, but the higher frequencies also imply worse radio conditions. Multi-connectivity, a feature of 5G that allows users to connect to more than one base station simultaneously, can offer the advantages of both interfaces. In this paper, we investigate how multi-connectivity can improve user reliability and the system’s energy efficiency. Five algorithms for secondary cell association are presented and evaluated. We show a decrease in the radio link failure rate of up to 50% at high speeds and improvements of the energy efficiency of up to 20% at low speeds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mobile networks are becoming more and more used throughout the world, and it is expected that the total mobile traffic will increase by a factor of ten in 2022 [1]. In addition, the cellular infrastructure of tomorrow should support new usages—for instance connected vehicles or for industry 4.0 type of applications. Such use cases imply higher requirements on the network, such as ultra-low latency or ultra high reliability [2]. Therefore, the current cellular networks might not be able to tackle this tremendous growth while providing a sufficiently good quality for the services of tomorrow. The next generation of mobile communications, 5G, has therefore been designed to overcome these issues [3].
In addition to the frequencies used by Long Term Evolution (LTE), 5G uses higher frequency bands with a new radio access technology called New Radio (NR). Multiple proposals on the frequencies have been studied: the 15 GHz band [4], the 28 and 38 GHz bands [5, 6], and the 60 GHz band [7, 8]. The next generation of cellular networks also relies on massive MIMO [9], beamforming [10], ultra-dense networks, and multi-connectivity to provide an improved quality of service.
However, the total energy consumption of the infrastructure is increasing for network operators. In 2011, base stations were already consuming 4.5 GW of power (or 20 Mt of CO2) annually [11]. In terms of cost, this equates to up to 18% of operational expenses in Europe, and up to 32% in India [12]. Gruber et al. [13] broke down the network’s power consumption and showed that base stations (BSs) alone represented around 57% of the entire network consumption. Han et al. [14] showed that between 50% and 80% of the BSs’ consumption is caused by the power amplifier, as shown in Fig. 1. This led the International Telecommunications Union (ITU) to consider energy efficiency as one of the key capabilities of 5G.
Multi-connectivity is a 5G technique allowing a user to connect to multiple BSs at the same time, potentially from different radio interfaces [15]. It is an extension of dual connectivity, already present in LTE, to more than two simultaneous links [16]. Dual connectivity and multi-connectivity have been showed to increase the throughput and reliability for the end users [17,18,19]. However, little attention has been given to the energy consumption and energy efficiency of multi-connectivity, both from the end user and the cellular infrastructure’s perspective.
In this paper, we investigate the effects of multi-connectivity on the network performance within an ultra-dense deployment.
We propose new algorithms for multi-connectivity and evaluate them, along with standard algorithms, to study their effects upon the energy efficiency of the cellular network when multi-connectivity is used. This paper makes the following contributions:
We introduce a general expression of the network’s energy efficiency when multi-connectivity is used, and estimate rough lower and upper bounds of its gains;
We introduce a general framework for secondary cell selection;
We design five algorithms for secondary cell association with a focus on improving the energy efficiency of the network;
Finally, we evaluate our proposals using simulations.
The remainder of this paper is organized as follows. In Sect. 2, we introduce ultra-dense networks and make a review of multi-connectivity algorithms. In Sect. 3, we formulate the energy efficiency of multi-connectivity and express its bounds. In Sect. 4, we present our framework for secondary cell association. In Sect. 5, we thoroughly explain our algorithms. In Sect. 6, we present the models used in our simulator. In Sect. 7, we evaluate through simulations our proposals. Finally, we conclude our work in Sect. 8.
2 Background and related work
In this section, we survey the literature regarding ultra-dense network and multi-connectivity. We then present how power consumption and base station sleep are modeled in 5G systems.
2.1 Ultra-dense networks
An ultra-dense network (UDN) is a new paradigm in which network densification is taken to the next level [20]. One way to define UDN is that UDN is a deployment in which the density of access nodes exceeds the density of users. Heterogeneous Networks (HetNets) paved the way for UDNs as small cells were used in the addition of the macro layer. Nodes far away from the macro-BS can connect to a smaller BS, with an improved received signal quality.
Low complexity nodes, such as micro or pico-cells, can be used in greater number to improve capacity. We refer the reader to [21] for an extensive survey on UDN.
UDN possesses four primordial characteristics: (i) users can be within the vicinity of multiple cells, (ii) interferences will be highly critical, (iii) cells will be free of users for most of the time, and (iv) in high frequency bands, line of sight deployment will be of great importance [21].
Thurfjell et al. [22] linked the system densification with an increase of the system throughput, and a densification threshold, after which the improvements decrease, was identified. Li et al. [23] expressed spectrum and energy efficiency of UDNs with stochastic geometry and also showed the improvements and limitations of network densification. Other works focus on new cell association schemes for HetNets and UDNs, such as game theory [24], a tier-level approach [25] or through heuristics [26].
2.2 Multi-connectivity
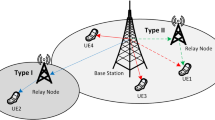
Multi-connectivity (MC) first appeared in 3GPP release 12 as Dual Connectivity (DC). DC is defined as an “operation where a given user equipment consumes radio resources by at least two network points connected with non-ideal backhaul” [16]. It is a special case of carrier aggregation, where carriers are served by different access points. MC is a refined version of DC supporting multi-Radio Access Technology (multi-RAT) [15]. From the DC definition, we define MC as: “The ability for a User Equipment (UE) to connect and consume radio resources from at least two access nodes simultaneously, both for inter-frequency and intra-frequency scenarios.” The architecture of multi-connectivity is depicted in Fig. 2 for two concurrent links. Inter-frequency MC will be enabled by a tight integration between the two air interfaces [27].
The usage of MC millimeter-wave beamforming is investigated in [28], and a novel channel quality measurement for uplink (UL) is proposed to assess the secondary cell candidates. In contrast, our work focuses on the downlink (DL) aspect of MC. Temesa et al. [19], investigated the reliability for pedestrians and car users. An MC scheme is proposed for cloud radio access network in order to improve mobility-related failures and throughput at the edges. In [19], the authors add secondary cells if their received signal is within a certain threshold from the main connection, and remove secondary cells if their signal falls below a second threshold.
While MC offers great benefits for downlink (DL) transmission, UL is a much more complex operation as a limited power budget must be shared across links. A decoupled spectrum aggregation has therefore been proposed in [29] to tackle the challenge of asymmetric UL/DL. The authors showed limited benefits from spectrum aggregation for UL, and described decoupled association for secondary cell.
Finally, Fast Switching (FS) is another approach to DC, where the resource consumption is quickly switched from one RAT to another depending on the network performance. In contrast, users using DC can potentially consume resources and benefit from all access points at the same time. Monteiro et al. [18] compared normal DC and fast switching. The authors use the Reference Signal Received Quality (RSRQ) metric to quickly switch from one RAT to another, therefore allowing a user to always benefit from the best RAT. It is shown that for high loads, FS outperforms DC.
2.3 Power consumption model
The most commonly used power consumption model for LTE has been formulated in the E3 (Energy Efficiency Evaluation) framework from the EARTH project [30], such as:
where \(N_T\) is the number of transceivers, \(N_S\) is the number of sectors, \(N_C\) the number of carriers, \(P_0\) the static power consumption caused by the cooling and signal processing, \(P_\mathrm{tx}\) the radiated power, \(\varDelta _P\) a constant, representing additional costs due to feeder losses and the power amplifier, \(P_\mathrm{max}\) the maximum radiated power and \(P_\mathrm{sleep}\) the power consumption when the base station is in sleep mode.
With the usage of the most energy-efficient hardware and more efficient signalling, 5G base stations will be more energy efficient than their LTE counterparts. Furthermore, it is envisioned that improved sleep modes will be available. Cells will go to sleep faster, more often and for longer periods of time. A breakdown of the base station’s components is done in [31], and partial deactivation of sub-components is seen as a way to optimize power consumption further. Figure 3 shows the envisioned sleep mode for 5G systems.

Adapted from [31]
Envisioned sleep levels in 5G
3 Formulation of energy efficiency
In telecommunications, the ITU defines energy efficiency as “the relationship between the specific functional unit for a piece of equipment and the energy consumption of that equipment” [32]. At the network level, this definition corresponds to the quantity of data transmitted at the physical layer by an equipment per unit of energy. It is expressed in (bit/J), although some works prefer to use the (J/bit) notation (i.e. the quantity of energy consumed to transmit one bit).
In this section, we analytically express the energy efficiency. We start by an ordinary, single connectivity scenario, and extends the expression for multi-connectivity. Then we express rough upper and lower bounds for the energy efficiency of MC.
3.1 Notations
In the remainder of this section, we refer to specific users and base stations based on their characteristics (e.g., their number of links or served users) with different notations. We here list all notations used throughout the section.
U refers to the set of all users connected to the network, and |U| refers to the total number of users. Similarly, C is the set of all cells (i.e., base stations) composing the network, and |C| indicates the total amount of cells. Without loss of generality, the cardinality of a set represents the number of elements of this set throughout this paper.
We further define \(C_\mathrm{used} \subseteq C\) as the subset of cells currently active and serving users. This subset allows us later to differentiate cells active from cells in sleep mode. Additionally, \(C_\mathrm{master} \subseteq C_\mathrm{used}\) are cells used as the main link in multi-connectivity, while \(C_\mathrm{sec} \subseteq C_\mathrm{used}\) contains all cells used as secondary cells.
Moreover, we further define \(U_c \subseteq U\) as the subset of users served by the cell c. In addition, \(U_\mathrm{MC} \subseteq U\) denotes the subset of users actively maintaining more than one link (i.e., users that benefit from multi-connectivity).
3.2 Energy efficiency’s expression
We first present a simple formulation for energy efficiency at the network level when users can connect to at most one base station. We later extend our expression to scenarios where multi-connectivity is possible.
3.2.1 Scenario 1: single connectivity
At the radio access network level, we define energy efficiency as the ratio between the quantity of transmitted data by the network and the operating cost of equipment in terms of power. For the former part, i.e., the quantity of transmitted data, we consider the system throughput as the sum of all communications in the user plane between users and their serving BSs. The control plane is discarded of this analysis and the evaluation. For the power consumption, we discard intermediary components, and only consider the consumption of base stations, as it represents the most important share of the operational cost of a cellular network [13].
We can write the energy efficiency \(\eta _\mathrm{SC}\) of a single connectivity (SC) system as:
where \(R_\mathrm{SC}\) is the system rate (for a single connectivity scenario) and \(P_\mathrm{SC}\) the power consumed by the system. \(R_\mathrm{SC}\) is further defined as:
where u is a user, U the set of active users in the network, \(R_\mathrm{master}(u)\) the downlink bitrate for the user u by its master cell. \(P_\mathrm{SC}\) is defined as:
where c is a cell, C the set of all cells within the network, \(C_\mathrm{used}\) a subset of C containing all the active cells, \(U_c\) the subset of users connected to the cell c, and \(P_{tx}(c,u) = P_\mathrm{tx}*\varDelta _P\) the non-constant part of Eq. (1). In simple terms, the system throughput is the sum of each user’s throughput and the power consumed is equal to the power consumed by the entire network in sleep mode, plus the cost of turning on the active BSs and the cost of transmitting data to the user.
3.2.2 Scenario 2: multi-connectivity
The previous expression of \(\eta _\mathrm{SC}\) covers all scenarios where only one link is allowed per user. For a scenario with multi-connectivity, the expression must be extended. We therefore write:
We further define the rate as:
where \(U_\mathrm{MC}\) is the set of active users using MC, \(C_\mathrm{sec,u}\) is the set of secondary cells the user u is connected to, and \(R_\mathrm{c}(u)\) the downlink bitrate from c to u.
This means that the system throughput in multi-connectivity is composed of the throughput of the main connection and of each additional connection, for each user.
The expression for \(P_\mathrm{MC}\) is similar to the one given for \(P_\mathrm{SC}\), except that the set \(C_\mathrm{used}\) now contains more elements, such as \(P_\mathrm{MC} \ne P_\mathrm{SC}\). More precisely, it contains the set of master cells that were already present in single connectivity, but additionally the set of secondary cells. Furthermore, we have \(R_\mathrm{MC} \ge R_\mathrm{SC}\). We can further expand the expression as:
where \(\delta _R(u) \in [0,1]\) represents the offloading factor between the master cell and secondary cells. In simple terms, the master cell does not need to provide an equivalent bandwidth in MC since a part of the load is served by the secondary cells.
This general expression, however, does not provide much insight to determine whether MC is more or less energy efficient than the classical, single connectivity, scenario. Therefore, we propose here to estimate the lower and upper bounds of this expression, and compare them with the energy efficiency of the same scenario with single connectivity.
3.3 Lower bound
Let us consider a scenario where the usage of MC induces an offloading of data from the primary cell towards the second. Moreover, let us also consider that this traffic steering does not provide any improvement towards the capacity, such as:
Regarding the power consumption, as in Eq. (7), the offloading induces a decrease in the transmitted power of the master cells, and an increase in the secondary cells, written as:
where \(C_\mathrm{sec}\) is the subset of cells containing all the BSs used for secondary links, \(C_\mathrm{master}\) the subset of C containing all the BSs used as master cell, \(U_c\) the subset of users connected to the cell c and \(\delta _P(u)\) the offloading factor associated to the user u. In simple terms, the power consumption of a network with MC is equivalent to the consumption of a network with single connectivity, plus the cost of activating the secondary cells that were otherwise sleeping, plus the cost of transmitting with the secondary cells, minus the energy we save by offloading some traffic. We can rewrite the expression as:
where \(\varDelta _\mathrm{offload} = \sum _{u \in U_c,c\in C_\mathrm{master}} \delta _P(u) * P_{tx}(c,u)\) and \(\varDelta _\mathrm{MC} = \sum _{c\in C_\mathrm{sec},c\not \in C_\mathrm{master}}\left( P_0(c)-P_\mathrm{sleep}(c)\right) + \sum _{u \in U_c,c\in C_\mathrm{sec}} P_{tx}(c,u).\)
Equation (10) is the simplified form of Eq. (9), and it is clear that the energy consumed in multi-connectivity corresponds to the energy consumed with single connectivity, plus the additional cost of MC (i.e., turning on more cells, transmitting using secondary cells), minus the cost of offloading some transmissions from the master cell to the secondary cells (e.g. if secondary cells are more energy efficient).
From Eqs. (8) and (10), we can express the energy efficiency as:
where the efficiency of multi-connectivity is therefore confined to its ability to less consuming transmitters. In the case of non-ideal backhaul, its impact should also be assessed within \(\varDelta _\mathrm{MC}\).
3.4 Low performance bound
A second and less general bound can be defined where we this time consider an increase in capacity with MC. We define in Sect. 4 a disconnection threshold. In simple terms, a secondary link is dropped if its quality falls below a fraction of the quality of the master link. This fraction is the disconnection threshold \(\theta _\mathrm{rmv}\). Here, we express it as a ratio of the bitrate offered by the master cell, such as \(\mathrm{threshold} = \theta _\mathrm{rmv}*R_\mathrm{master}\). Therefore, we consider a worst-case scenario using the following assumptions:
Assumption 1 Each secondary cell serves at most one user.
This assumption ensures us that the power consumption is maximized. Moreover, it is a reasonable assumption with few users, such as in an ultra-dense network.
Assumption 2 We consider that the multi-connectivity feature induces an increase in the system throughput such as \(R_\mathrm{MC} > R_\mathrm{SC}\), i.e. , \(\delta _R(u) < 1\).
We can express the system rate as:
such as:
where \(|U_\mathrm{MC}| = \Pr (u \in U_\mathrm{MC})*|U|\) is the number of users with multiple links, and can also be defined as the factor of the total number of users and the probability that one user can have multiple links, \(mean(|C_\mathrm{sec,Umc}|)\) the average cardinality of \(C_\mathrm{sec,u}, \forall u \in U_\mathrm{MC}\), which corresponds to the mean number of additional connections for a user in MC. For the lower bound, we consider that users have their primary and one secondary link only.
In a similar manner, \(P_\mathrm{MC}\) can be simplified as:
where \(c\in C_\mathrm{sec},c\not \in C_\mathrm{master}\) represents a cell element used as a secondary cell that is not used as a master cell for another user, and \(\varDelta _\mathrm{P,lwr}\) the evolution of the consumed power related to MC such as:
We can thus describe the energy efficiency of an MC scenario as:
where \(\varDelta _\mathrm{R,lwr}\) and \(\varDelta _\mathrm{P,lwr}\) are defined in Eqs. (13) and (15) respectively.
3.5 Upper bound
Now that we have a rough lower bound of the MC energy efficiency, we try to determine a possible upper bound. In reality, determining the actual upper bound is a difficult task, since the network deployment, the users’ positions and the traffic affect the result. We once again only provide a rough upper gain, in order to estimate potential gains of using multi-connectivity..
We again assume two characteristics:
Assumption 1 Each secondary cell serves at most one user.
Ideally, all resources of a secondary cell are used to serve the same user, maximizing its bitrate.
Assumption 2 Each user is connected to as many secondary cells as it is physically possible.
By doing so, we maximize the maximal achieviable bitrate for each user.
We therefore obtain:
where \(R_\mathrm{max}(c,u)\) is the maximum achievable bitrate between u and c, \(max(|C_\mathrm{sec,Umc}|)\) the maximum number of secondary link that a user can handle, \(mean(R_\mathrm{max}(c,u))\) the average maximum achievable bitrate taken for all users and
The power consumption follows a similar evolution as for the lower bound, such as:
where the power transmitted is maximized as we are using all available resources.
Therefore, from Eqs. (18) and (20), we can express the energy efficiency of MC as a bounded value such as:
3.6 Ensuring energy efficient multi-connectivity
Following Eqs. (16) and (21), the energy efficiency of multi-connectivity can be written as:
It can be of great interest to compare the lower bound against the evolution of \(\eta _\mathrm{SC}\), such as we can decide under which conditions MC is more energy efficient than single connectivity. To do so, we search parameters such as:
By choosing the right value for the disconnection threshold, it is therefore possible to ensure that MC is more energy-efficient than single connectivity, as it is shown in Sect. 7.
4 Secondary cell association
Numerous ways of selecting secondary base stations are possible. In this section, we propose a framework that serves as a basis for our secondary cell association. Then, we present a metric that can be used to assess the impact on the energy efficiency of the choice of the secondary cell.
4.1 Framework for target selection and association
First of all, it is important that secondary cell association follows similar mechanisms as normal handovers. Specifically, the same channel measurement mechanisms must be shared by the two procedures in order to limit signaling overhead.
As for handover, it is crucial to avoid the ping pong effect for secondary link. We recall that the ping pong handover happens when a user is at the edge of two cells and constantly connects and disconnects from one cell to the other following channel disturbances, causing a decrease of the system performance and an unnecessary waste of resources.
In our framework, we decouple connection and disconnection into two distinct procedures. Unlike the primary connectivity, we do not want secondary links to be maintained at all time. In our vision, a secondary link should be established only in order to boost performance, and should not become a burden on the system when the conditions are not optimal.
A counter, called Time To Trigger (TTT), is used to avoid the ping pong effect. A target for association must meet the criterion for the counter duration before the connection procedure is launched.
Additionally, two thresholds are used for connection and disconnection. \(\theta _\mathrm{add}\) and \(\theta _\mathrm{rmv}\) quantify both thresholds, respectively. A secondary link is created if the measured metric is higher than the main connection multiplied by \(\theta _\mathrm{add}\). Similarly, a secondary link is dropped if its quality drops below the quality of the main link multiplied by \(\theta _\mathrm{rmv}\).
Figure 4 represents the process of selecting a target for secondary association. Our disconnection procedure follows a similar process, and is therefore not depicted.
For the cell association, numerous metrics can be taken as input for an algorithm. We classify them in four categories:
Robustness this class regroups the most common metrics, such as Reference Signals Received Power (RSRP), Received Signal Strength Indicator (RSSI) or the Signal over Interference plus Noise Ratio (SINR), and are used to estimate the channel or signal quality. Optimizing these metrics allows to select more robust links.
Performance Estimating the achievable bitrate can be used as a metric to increase the performance of the system.
Energy the power consumption can be used as a metric when designing energy efficient algorithms. Realistic power models are however necessary.
Cell utilization Metrics such as the cell load, the number of connected devices or the base station’s state can also be used as inputs.
4.2 Energy efficiency condition
When comparing potential base stations for secondary cell association, it might be of interest to also take into account the power consumption. Indeed, substantial savings can be made if part of the transmission can be done on a small cell, as expressed in Eq. (11). here, we therefore propose a condition comparing the cost, in terms of power consumed, when transmitting data for a user on its main connection or if it was using a secondary cell. It can be written as:
where \(P_C(t)\) represents the power consumed at time t by the system, such as \(P_{C \mid M}(t)\) is the power consumed knowing that the data was transmitted by the master cell, and \(P_{C \mid S}(t)\) when transmitting all the data by the secondary cell. In simpler terms, we can consider that it is more energy efficient to associate to a secondary cell if the power consumed while transmitting with it is lower than the power consumed by simply transmitting the same amount of data on the master link.
The expression can be extended by considering only the master BS and the potential secondary cell. We now have:
where \(P_{\mathrm{C,master}}\) represents the power consumed by the master BS and \(P_{\mathrm{C,sec}}\) the power consumed by the secondary cell.
By considering the evolution between the time t, where the transmission starts, and \(t-1\), we can simplify the expression such as:
Assumption The rest of the traffic is constant between \(t-1\) and t.
This can be seen as a pretty strong assumption. However, in downlink, knowledge of the future traffic can be obtained by looking at the buffer, which can relax the assumption. Furthermore, considering multiple users at the same time while assessing the condition can also relax this assumption.
Using this assumption, the condition can be further simplified as:
Such as the evolution of consumption when transmitting using the master cell should be higher than the evolution of consumption using the secondary cell to consider MC as more energy-efficient.
Using the power model defined in Eq. (1), we obtain the formal expression:
where \(P_0\) is the constant consumption in active mode (from Eq. (1)), \(P_\mathrm{TX}\) the radiated power, \(P_{\mathrm{TX,u}\mid \mathrm{M or S}}\) the radiated power related to the transmission for user u, \(\varDelta _P\) the slope relative to the dynamic power consumption and \(P_C(t)\) the power consumed at the time t.
We define \(\varDelta P_\mathrm{C}(t)\) as the evolution of the power consumption, i.e. \(\varDelta P_\mathrm{C}(t) = P_\mathrm{C}(t) - P_\mathrm{C}(t-1)\). We use this definition only to simplify the expression, as it does not change the content. We can now formulate our condition as:
where
5 Cell association algorithms
Using the framework described in Sect. 4.1, we propose five different implementations for secondary cell association. The parameters used for the TTT counter and the thresholds are summarized in Table 1. Table 2 summarizes in which classification their inputs are taken from. Four algorithms try to maximize performance, i.e., the throughput. Two of them try to improve the robustness of the connectivity. Among these five algorithms, three of them implement the energy efficiency condition described above.
5.1 Max bitrate
We first introduce a simple, well-known optimization metric in the literature: the throughput. The cell association algorithm’s goal is to maximize the user throughput, for a given user. It serves as a baseline for more complex algorithms and performance evaluation. Here, we calculate the capacity using the Shannon Law, such as \(R_u(c) = BW_c*log_2(1+\gamma _u(c))\) where c is a cell, u a user, \(\gamma _u(c)\) the SINR of the downlink connection between c and u, and \(BW_c\) the full bandwidth of c. It is important to note that, unlike maximizing the SNR only, this algorithm takes into account the bandwidth difference of each RAT. We thus only require knowledge of the bandwidth size and the channel quality to estimate the throughput. Much more precise estimations can be made, for example by taking into account the number of available resources. However, the improvements in terms of performance are rather low, especially considering the increased complexity of the resulting algorithm.
Let us denote the set of candidates for association as:
where \(c_m\) is the master cell of u, C the set of all BSs, and \(\theta _\mathrm{add}\) the connection threshold. The candidates are therefore the subset of the set satisfying the condition on the throughput, such as the offered throughput of a candidate must be higher than a fraction of the master cell throughput. We set \(\theta _\mathrm{add} = 0.8\) (see Table 1), which is equivalent to say that a candidate must be at least 80% as good as the master cell in terms of throughput to be considered worthy. Values of the parameters were selected through simulation testing.
We then select the best cell among the candidate and set it as target for association:
We follow a similar principle for the disassociation procedure. We test each throughput provided by the secondary cells against the master cell bitrate, and disconnect the ones that fall below the threshold. We note the subset of cells to remove as:
where \(C_\mathrm{sec}(u)\) is the set of secondary cells of u, and \(\theta _\mathrm{rmv}\) the disassociation threshold. We set the threshold to \(\theta _\mathrm{rmv} = 0.5 < \theta _\mathrm{add}\) such as the hysteresis is maintained.
One could wonder why both selection procedures must be based on the primary link characteristics, while there is no obligation to do so. We base our thresholds on the master bitrate simply because there is no proof beforehand that the best candidate would provide sufficient improvements without such constraint.
5.2 Max SINR
While the previous algorithm aimed at maximizing the performance, the goal of this one is to improve the users’ robustness. Indeed, for some high reliability applications, maintaining the communication channel at all time might be critical. Multi-connectivity can be of great interest for such scenarios. We introduce another well-known solution in the literature, using the SINR as optimization metric for the cell association algorithm. . We now write our set of candidates as:
where \(\gamma _u(c)\) represents the SINR of the downlink between the cell c and the served user u.
This time again, our threshold is dependent on the master link quality. For high reliability applications, however, selecting the best candidates and maintaining the connection without taking into account the ratio with the master might provide better results in terms of robustness, at the price of an increase in power consumption.
We then select the best targets as before:
The disassociation follows the same principle as before.
5.3 Max bitrate-EE
We showed in Sect. 4.2 that a condition can be defined on the power condition in order to ensure energy efficiency. We therefore decide to expand the Max Bitrate algorithm and include this condition as a metric for the selection of secondary cell.
where \(C_{\theta add}\) is defined in Eq. (31), \(P_{\mathrm{C} \mid c_{i}}(t)\) is the power consumed by the system when the data is transmitted by the cell \(c_i\), as expressed in Eq. (24).
It has to be noted that the condition is applied on top of the throughput condition, such as only candidates that satisfy both conditions as considered. Another algorithm presented later will relax this constraint.
No changes are made on the disconnection rule. We simply consider that once the connection is established, keeping it active does not cost extra energy, since the cell is already active, and as long as the link does improve the throughput, the association stays.
5.4 Max clustered-bitrate
Previous algorithms greedily try to maximize each user’s throughput. Now, we propose an algorithm that considers several users at once, and tries to group them to connect to the same secondary cell. The goal is to minimize the number of cells to turn on, therefore minimizing the increase of power consumption.
We consider a matrix \({\mathbf {A}}\) of size \(M \times N\), where M is the number of users and N the number of cells.
The matrix \({\mathbf {A}}\) is then filled following this principle:
where \({\text {R}}_i(c)\) is the downlink bitrate for the user i from the cell c.
We therefore have \({\mathbf {A}}_{ij} \in \{0\} \cup [1,+\infty [\). Although it can tend to infinity, \(A_{ij}\) is unlikely to exceed 10 (i.e., no secondary cell can provide more than ten times the throughput of the master cell).
We can then choose a target for a group of users such as:
where \(\sum _i {\mathbf {A}}_{ij}\) represents the quantity of improvement the cell j can provide to the group of users. Therefore, every user u where \({\mathbf {A}}_{uc_{\text {target}}} \ne 0\) will connect to the cell \(c_\mathrm{target}\). We fix \(\theta _{clst} = 0.8\) as before, which means this time that the collective improvement should be of 80% at least, and the local improvement is fixed by \(\theta _\mathrm{add}\). Here, a lower \(\theta _\mathrm{add}\) can be used compared to the previous algorithms for better results.
5.5 Analytic hierarchy process
The Analytic Hierarchy Process (AHP) technique is a common tool used in multi-criterion decision making and proposed by Saaty [33]. Its principle consists in dividing a goal within sub-problems, and attributing a weight to every sub-problem, such as the sum of the weight is equal to 1. Each alternative is then tested and given a score between [0, 1] for each problem and a weighted sum is done to obtain the final score. The general formulation is given by:
where S(x) is the final score of the solution x, \(w_i\) the weight of the criteria i and \(S_i(x)\) the individual score of x for the criteria i.
In our implementation, the main goal is the selection of the best target for secondary cell association. We therefore define three sub-problems: the performance of a candidate cell, its robustness and whether it satisfies the energy efficiency condition. We can thus write our implementation of AHP as:
where
In our implementation, we fix \(w_\mathrm{perf} = 0.5\), \(w_\mathrm{robust} = 0\) and \(w_\mathrm{EE} = 0.5\) in order to maximise the performance while taking into account the energy efficiency. Although we do not use the robustness, we keep it in the formulation as it makes it easier to adapt the algorithm to a specific situation.
6 System models
A MATLAB-based simulator is used to evaluate our proposals. In this section, we describe the different models implemented.
6.1 Power consumption model
We use the power consumption model given in Eq. (1) for LTE cells. We only consider one sleep level for this RAT, as previous deployment might be used for macro-coverage. In contrast, we consider a more energy efficient hardware for NR, and envision two sleep levels, called micro-sleep, corresponding to the actual level of LTE, and deep sleep. Therefore, we can extend our power consumption model from Eq. (1) for NR such as:
where the sleep mode 1 is the so-called micro-sleep and the sleep mode 2 the deep sleep. \(\delta _\mathrm{NR}\) is an efficiency factor of the RAT from the lean design, as used in [34]. Table 3 summarizes the parameters used in our power consumption model.
We consider a sleep mechanism based on the DL activity and the number of users connected to a cell. A cell without any user connected and without activity will go to sleep, and wake up periodically to send signals for channel quality assessment. A master cell with at least one user will always stay awake no matter the activity. If a BS is only used as a secondary cell, it can go to sleep since the master cell will handle any UL transmission. The sleep mechanism is implemented as follows:
After 10 ms in active mode and without any activity, the base station goes to the sleep level 1;
The base station wakes up directly if it needs to transmit something, or a user connects. Without any activity, the base station stays in sleep level 1 for a maximum duration of 10 ms. After that time, it goes into sleep level 2.
The base station stays in sleep level 2 until an activity is detected. When there is any activity, it goes directly into active mode.
6.2 Traffic model
The METIS project recommends modeling traffic as bursty, user-driven flows for dense urban information society simulations in [35]. We therefore use the 3GPP FTP 2 model as defined in [36]. In order to emulate the diversity of flows of data traffic, chunks are generated with three possible lengths: 1 MB, 10 MB and 100 MB, where the size follows a discrete exponential distribution. Chunks size is independent of any previously generated chunks form the same user. The inter-arrival time between two independent chunks also follows an exponential distribution with a mean of 3 s.
6.3 Network model
An ultra-dense deployment is modeled by a multi-tier network. The deployment is disposed as a hexagonal grid with a wrap-around parameter, such as the network is repeated infinitely and edge cells receive interferences from other cells outside the area of interest. The area of interest measures 0.63 km2.
Evolved-LTE is used for the macro-layer and consists of three tri-sector sites, accounting for 9 cells, with an inter-site distance of 400 m. The micro-layer is composed of 61 New Radio sites, and uses omnidirectional small cells with an inter-site distance of 100 m. Evolved-LTE runs at 2 GHz with a carrier bandwidth of 20 MHz, while NR runs at 28 GHz with a carrier bandwidth set to 100 MHz to model the better performances of the RAT. Figure 5 depicts the deployment used in the simulations and Table 4 summarizes its parameters.
7 Simulation results
We evaluate our proposals through simulations. Experiments are repeated for a single connectivity scenario and for each algorithm for identical parameters. Users are modeled by a homogeneous PPP distribution and follow a linear movement model with a fixed velocity of 3 km/h.
7.1 Robustness and user throughput
The user performance is evaluated through its connection robustness and the 10th percentile user throughput. In Fig. 6a, the Radio Link Failure (RLF) rate is evaluated at different velocities and for different numbers of simultaneous connections with the Max SINR algorithm. At low velocities, little improvement appears from multi-connectivity. At high velocities, however, maintaining two connections offers a decrease in the RLF rate of up to 33% while three simultaneous links offer a decrease of up to 49%. The benefits of adding more links seem to decrease as the number of simultaneous links increases.
As expected, multi-connectivity does increase the user throughput, as more resources are available to claim, as shown in Fig. 6b. Three of the algorithms, namely Max Bitrate, Max Bitrate-EE and AHP, provides an improvement of 70% or more. AHP obtains the highest results, with improvements around 75%, while the others are around 70%. Max Clustered-Bitrate does not perform as well and obtains an average improvement of 34% compared to single connectivity. With few users, the improvement is below 10%, and increases to around 60% as the number of users increases. This is due to the fact that the algorithm groups users towards the same secondary cell, which is not the most optimal from the user perspective.
7.2 Network-level metrics
In this section, we focus on the network performance and give a special interest to the evolution of power consumption and energy efficiency.
7.2.1 Power consumption
Figure 7a depicts the consumed power of the network, i.e., the power consumed by all base stations. With Max Bitrate, which does not implement the energy efficiency condition, we see an increase of 3.9% compared to single connectivity. Max Bitrate-EE and AHP, which both implements the condition, induce an increase of 2.7% and 2.8% respectively. Furthermore, we can see that Max Clustered-Bitrate, which aims at minimizing the number of active cells, does induce a decrease of 1.5% compared to single connectivity. This is simply due to the fact that using a small BS is sometimes more efficient than transmission using a macro-cell.
7.2.2 System energy efficiency
Figure 7b compares the energy efficiency performance of each algorithm against single connectivity. The results show that all our MC algorithms outperform the single connectivity scenario, regardless of the number of active users. We see an improvement of up to 43.8% with three of them, namely Max Bitrate, Max Bitrate-EE and AHP, when the number of users is very low. On average, we see an increase of energy efficiency of 13.1% with Max Bitrate, 13.9% with Max Bitrate-EE and 14.2% with AHP. Max Clustered-Bitrate obtains poorer results with an improvement of 2% by average and up to 3.6% with 65 users. Similar to the power consumption, we see that the energy efficiency condition does increase the algorithm’s performance in terms of energy efficiency.
We now compare the results of Max Bitrate and Max Bitrate-EE against the low performance bound expressed in Sect. 3.4. A disconnection threshold of 0.5 is used in the formula. Figure 8 depicts the comparison through the entire simulated range. Above 70 users, the number of users is higher than the number of cells, which falsify the assumption 1 of the bound. We therefore only consider the results below 65 users, while the whole range is showed to draw a parallel with Fig. 7b. We can observe that the bound is always above single connectivity. This means that every algorithm implementing our proposal will be more energy efficient than single connectivity with an improvement of at least 7%. Max Clustered-Bitrate is not shown as its principle is in contradiction with the first assumption of the low performance bound.
7.2.3 Probability of multi-connectivity
As per our framework design, we do not wish to constantly maintain secondary links. We investigate how many users are using more than two simultaneous links, and infer the probability of a user being in multi-connectivity from this measure. Table 5 summarizes our findings. We can observe that the implementation of the energy efficiency condition between Max Bitrate and Max Bitrate-EE causes a decrease of around 2.8%. AHP, however, sees a reduction of 2.4% only. This is due to the fact that Max Bitrate-EE removes candidates that do not satisfy the condition, whereas compliant candidates improve their score in AHP. Once again, Max Clustered-Bitrate obtains the poorest results. It should however be noted that its performance varies greatly with the number of users present in the network. With few users, only around 10% are in MC while the probability increases up to 17% with many users.
8 Conclusion
In 5G systems, users can connect to two different radio air interfaces, Evolved-LTE and New Radio, each interface offering different benefits and drawbacks. Multi-connectivity, the ability for a user to connect and consume resources from multiple access points concurrently, is seen as a way to benefit from both interfaces at the same time. This work investigates multi-connectivity in ultra-dense 5G networks from the network’s energy efficiency perspective. We propose new algorithms for secondary cell selection, aimed at improving robustness and performance, while minimizing the energy impact of maintaining several links per user. To do so, we introduce a new condition for secondary cell selection based on the estimated energy efficiency gain.
Our evaluation shows that (a) multi-connectivity allows a reduction of up to 50% of radio link failures at high speeds and (b) our novel secondary cell selection allows an improvement of up to 20% of energy-efficiency of the network, compared to the absence of multi-connectivity. Two algorithms, Max Bitrate-EE and AHP, use the energy efficiency condition and are shown to outperform algorithms not considering energy efficiency as part of their metrics.
Additional work must be done to investigate the effect of multi-connectivity on the end user, especially concerning the energy efficiency of user equipment.
References
Ericsson mobility report. Technical report (2016).
[Draft] minimum requirements related to technical performance for IMT-2020 radio interface(s). Technical report (2017). https://www.itu.int/pub/R-REP-M.2410-2017.
Andrews, J. G., Buzzi, S., Choi, W., Hanly, S. V., Lozano, A., Soong, A. C. K., et al. (2014). What will 5G be? IEEE Journal on Selected Areas in Communications, 32(6), 1065–1082.
Okvist, P., Asplund, H., Simonsson, A., Halvarsson, B., Medbo, J., & Seifi, N. (2015). 15 GHz propagation properties assessed with 5G radio access prototype. In 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE.
Rappaport, T. S., Sun, S., Mayzus, R., Zhao, H., Azar, Y., Wang, K., et al. (2013). Millimeter wave mobile communications for 5G cellular: It will work!. IEEE Access, 1, 335–349.
Roh, W., Seol, J. Y., Park, J., Lee, B., Lee, J., Kim, Y., et al. (2014). Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results. IEEE Communications Magazine, 52(2), 106–113.
Yilmaz, T., Fadel, E., & Akan, O. B. (2014). Employing 60 GHz ISM band for 5G wireless communications. In 2014 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom). IEEE.
Daniels, R., & Heath, R. W, Jr. (2007). 60 GHz wireless communications: Emerging requirements and design recommendations. IEEE Vehicular Technology Magazine, 2(3), 41–50.
Lu, L., Li, G. Y., Swindlehurst, A. L., Ashikhmin, A., & Zhang, R. (2014). An overview of massive MIMO: Benefits and challenges. IEEE Journal of Selected Topics in Signal Processing, 8(5), 742–758.
Vook, F. W., Ghosh, A., & Thomas, T. A. (2014). MIMO and beamforming solutions for 5G technology. In 2014 IEEE MTT-S International Microwave Symposium (IMS2014). IEEE.
Bogucka, H., & Conti, A. (2011). Degrees of freedom for energy savings in practical adaptive wireless systems. IEEE Communications Magazine, 49(6), 38–45.
Humar, I., Ge, X., Xiang, L., Jo, M., Chen, M., & Zhang, J. (2011). Rethinking energy efficiency models of cellular networks with embodied energy. IEEE Network, 25(2), 40–49.
Gruber, M., Blume, O., Ferling, D., Zeller, D., Imran, M. A., & Strinati, E. C. (2009). EARTH—Energy aware radio and network technologies. In 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications. IEEE.
Han, C., Harrold, T., Armour, S., Krikidis, I., Videv, S., Grant, P., et al. (2011). Green radio: Radio techniques to enable energy-efficient wireless networks. IEEE Communications Magazine, 49(6), 46–54.
Technical specification group radio access network; evolved universal terrestrial radio access (E-UTRA) and NR [Draft]; multi-connectivity; stage 2 (release 15). Technical report (2017).
Technical specification group radio access network; study on small cell enhancements for E-UTRA and E-UTRAN; higher layer aspects (release 12). Technical report (2013).
Huang, P. H., Sun, S. S., & Liao, W. (2017). GreenCoMP: Energy-aware cooperation for green cellular networks. IEEE Transactions on Mobile Computing, 16(1), 143–157.
Monteiro, V. F., Ericson, M., & Cavalcanti, F. R. P. (2017). Fast-RAT scheduling in a 5G multi-RAT scenario. IEEE Communications Magazine, 55(6), 79–85.
Tesema, F. B., Awada, A., Viering, I., Simsek, M., & Fettweis, G. P. (2015). Mobility modeling and performance evaluation of multi-connectivity in 5G intra-frequency networks. In 2015 IEEE Globecom Workshops (GC Wkshps). IEEE.
Gotsis, A., Stefanatos, S., & Alexiou, A. (2016). UltraDense networks: The new wireless frontier for enabling 5G access. IEEE Vehicular Technology Magazine, 11(2), 71–78.
Kamel, M., Hamouda, W., & Youssef, A. (2016). Ultra-dense networks: A survey. IEEE Communications Surveys & Tutorials, 18(4), 2522–2545.
Thurfjell, M., Ericsson, M., & de Bruin, P. (2015). Network densification impact on system capacity. In 2015 IEEE 81st Vehicular Technology Conference (VTC Spring). IEEE.
Li, Q., Wu, G., & Hu, R. Q. (2013). Analytical study on network spectrum efficiency of ultra dense networks. In 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE.
Sun, Y., Chang, Y., Hu, M., & Wang, B. (2015). A cluster-based hybrid access strategy using non-cooperative game theory for ultra-dense HetNet. In 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems. IEEE.
Ye, Q., Rong, B., Chen, Y., Al-Shalash, M., Caramanis, C., & Andrews, J. G. (2013). User association for load balancing in heterogeneous cellular networks. IEEE Transactions on Wireless Communications, 12(6), 2706–2716.
Corroy, S., Falconetti, L., & Mathar, R. (2012). Dynamic cell association for downlink sum rate maximization in multi-cell heterogeneous networks. In 2012 IEEE International Conference on Communications (ICC). IEEE.
Silva, I. D., Mildh, G., Rune, J., Wallentin, P., Vikberg, J., Schliwa-Bertling, P., & Fan, R. (2015). Tight integration of new 5G air interface and LTE to fulfill 5G requirements. In 2015 IEEE 81st Vehicular Technology Conference (VTC Spring). IEEE.
Giordani, M., Mezzavilla, M., Rangan, S., & Zorzi, M. (2016). Multi-connectivity in 5G mmWave cellular networks. In 2016 Mediterranean Ad Hoc Networking Workshop (Med-Hoc-Net). IEEE.
Lema, M. A., Pardo, E., Galinina, O., Andreev, S., & Dohler, M. (2016). Flexible dual-connectivity spectrum aggregation for decoupled uplink and downlink access in 5G heterogeneous systems. IEEE Journal on Selected Areas in Communications, 34(11), 2851–2865.
Auer, G., Giannini, V., Desset, C., Godor, I., Skillermark, P., Olsson, M., et al. (2011). How much energy is needed to run a wireless network? IEEE Wireless Communications, 18(5), 40–49.
Debaillie, B., Desset, C., & Louagie, F. (2015). A flexible and future-proof power model for cellular base stations. In 2015 IEEE 81st Vehicular Technology Conference (VTC Spring). IEEE.
Recommendation ITU-T L.1310: Series l: Construction, installation and protection of cables and other elements of outside plant; energy efficiency metrics and measurement methods for telecommunication equipment. Technical report (2014).
Saaty, T. L. (1990). How to make a decision: The analytic hierarchy process. European Journal of Operational Research, 48(1), 9–26.
Tombaz, S., Frenger, P., Athley, F., Semaan, E., Tidestav, C., & Furuskar, A. (2015). Energy performance of 5G-NX wireless access utilizing massive beamforming and an ultra-lean system design. In 2015 IEEE Global Communications Conference (GLOBECOM). IEEE.
Deliverable D6.1—Simulation guidelines. Technical report (2013).
Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA),Further advancements for E-UTRA physical layer aspects (Release 9). Technical report (2010).
Klimova, A., Rondeau, E., Andersson, K., Porras, J., Rybin, A., & Zaslavsky, A. (2016). An international master’s program in green ICT as a contribution to sustainable development. Journal of Cleaner Production, 135, 223–239.
Poirot, V. (2017). Energy-efficient multi-connectivity for ultra-dense networks. Master Thesis. http://ltu.diva-portal.org/smash/record.jsf?pid=diva2%3A1136634&dswid=-5012.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Poirot, V., Ericson, M., Nordberg, M. et al. Energy efficient multi-connectivity algorithms for ultra-dense 5G networks. Wireless Netw 26, 2207–2222 (2020). https://doi.org/10.1007/s11276-019-02056-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-019-02056-w