Introduction

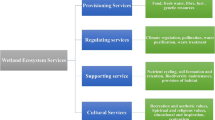
The global extent of inland wetlands has declined by almost 70% during the twentieth century mainly due to land-cover change for agricultural production (Davidson 2014). This rate of wetland conversion has continued into the twenty-first century (Gardner et al. 2015) with the associated loss of many important ecosystem services (Leemans and De Groot 2003). Wetlands play an essential role in maintaining water quality by removing excess nutrients and pesticides that can degrade downstream water quality, especially on agricultural landscapes (Vymazal 2017). Wetlands also modify water quantity by storing water and regulating and recharging aquifers thereby mitigating flooding in wet periods and supporting agricultural production during drier periods (Dixon and Wood 2003). The role of water regulation is particularly crucial for conserving freshwater, a critical resource for community welfare and agricultural production. Other identified wetland ecosystem services include carbon sequestration, recreation, tourism, human and livestock foods, and habitat to support diverse biotic communities (e.g., Davies et al. 2008; Badiou et al. 2011; Gleason et al. 2011; De Groot et al. 2012).

Wetland ecosystem services have many of the characteristics of public goods and are rarely or incompletely traded in economic markets (e.g., habitat for biodiversity, water quality), and there is an incomplete understanding of the link between changes in ecosystem structure and function, and the goods and services that are produced for society (Mitsch and Goesselink 2000; Brander et al. 2006). As a result, it is often challenging to assign a monetary value for many wetland ecosystem services that could be used in, for example, cost–benefit and tradeoff analyses, land-use planning, and wetland-conservation policy development. To overcome this challenge, a range of methods have been tested and adapted to estimate the monetary value of wetland ecosystem services, hereafter referred to as wetland values.

The completion of site-specific studies that can be used to estimate representative monetary values of local wetland ecosystem services requires the investment of considerable time and resources and as a result is not always practical for program and policy development. As a lower cost alternative, benefit transfer methods may often be used to supply information from comparable areas on ecosystem service values for policy decision-making. There are two main benefit transfer methods: (1) a unit value benefit, and (2) a benefit transfer function (Smith and Pattanayak 2002; Johnson et al. 2015; Richardson et al. 2015). Unit value benefit transfer uses a single estimate of environmental resource value from past research to infer the value of similar but separate environmental resources elsewhere (Smith and Pattanayak 2002). Benefit transfer function (meta-regression benefit transfers) use statistical models (meta-regression) to synthesize many environmental resource values from different past research studies and describe how the values change with the characteristics of the studies. It has been shown that, compared to unit value, meta-regression benefit transfers produce lower transfer errors and may generate the most reliable benefit transfer values (Rosenberger and Loomis 2000; Richardson et al. 2015). Several studies have conducted meta-regression analysis on wetland values (Brouwer et al. 1999; Mitsch and Gosselink 2000; Woodward and Wui 2001; Brander et al. 2006, 2007; Ghermandi et al. 2010; Chaikumbung et al. 2019), but these studies did not focus on agricultural wetlands, and the values of wetlands located on agricultural landscapes were often overlooked or misrepresented. Moreover, since wetlands are increasingly being converted to annual crop production in agroecosystems (Watmough and Schmoll 2007; Oliver et al. 2015; Peimer et al. 2017), we urgently need more comprehensive valuations of management alternatives to inform the protection and restoration of wetlands in agricultural regions and other high-valued resource areas (e.g., Turner et al. 2021).

The incentive to drain wetlands for agricultural production in developed countries has been driven by factors such as the increasing cost of farming around field obstructions with larger agricultural equipment, and the lower cost of wetland drainage with tools such as precision water management, GPS aided ditching, improved tile drainage equipment, and other engineering tools (Cortus et al. 2011; De Laporte 2014). In developing countries, increasing human population pressures and climate change are also motivating land managers to convert wetlands to agricultural lands (Dixon and Wood 2003). However, few studies have focused on estimating wetland values on agricultural landscapes, and so the overall estimated values of natural wetlands in agricultural areas are currently underestimated and therefore potentially misunderstood or ignored by the public. A notable exception is work by Brander et al. (2013) who conducted a meta-analysis on ecosystem services provided by wetlands in agricultural landscapes with an emphasis on three regulating ecosystem services: flood control, water supply, and nutrient recycling. These authors estimated average values for flood control, water supply and nutrient recycling to be $6923, $3389, and $5788 US$/ha/year, respectively.

The main objectives of this study are to estimate wetland meta-regression functions for factors that drive the value of wetland regulating services and wetland provisioning services on agricultural landscapes, and to examine the potential for using these functions to guide the benefit transfer of wetland values in agricultural landscapes globally. Our study builds on the work of Brander et al. (2013) by including additional wetland regulating services and provisioning services, creating a more comprehensive analysis of all wetland values (see Appendix Table 7); we excluded cultural and regulating services because of insufficient data. Schuyt and Brander (2004), Meyerhoff (2004), Jenkins et al. (2010), and Simonit and Charles (2011) describe nutrient recycling, nutrient mitigation, and nutrient retention wetland ecosystem services, respectively, as regulating service because they contribute to a healthy environment (Appendix Table 7); this classification is consistent with Brander et al. (2013) who classified nutrient retention as a regulating ecosystem service. Since the ecosystem services in the separate meta-regressions will be comparable in the way they regulate environmental processes or provide goods and services to society, and do not overlap, we are able to avoid commodity inconsistency problems (Vedogbeton and Johnson 2020). Commodity inconsistency occurs when total ecosystem values in meta-regression analyses incorporate a broad range of wetland ecosystem services that often overlap and are difficult to compare due to their different impacts on society (Brander et al. 2013). Commodity inconsistency, which could cause biased meta-regression estimates and incorrect inferences or benefit transfers, has been identified as a problem in previous wetland value studies (Brander et al. 2013; Vedogbeton and Johnston 2020).

Methodology

Systematic review

We completed a quantitative review of the results from published studies that analyzed or documented specific ecosystem services of wetlands within agricultural landscapes. A list of 668 research articles published prior to 2020 was generated using the keywords ‘ecosystem service OR economic’ AND ‘agricultural wetlands OR agriculture AND wetlands’ in the database of ISI Web of Science and with the Environmental Valuation Reference Inventory.

From these 668 papers, we examined each title and abstract to determine whether papers met the following criteria for inclusion in the meta-analysis: (i) reported quantifiable effects, (ii) provided the extent of wetland area change, (iii) listed a study location, and (iv) referred to wetlands in an agricultural context. This screening process identified 192 papers, which were reviewed in full to determine whether they contained relevant and usable data on agricultural freshwater wetlands. Papers were excluded if they measured coastal wetlands, peatlands or constructed artificial wetlands for waste management systems. From this subset, papers were excluded that did not provide (i) sufficient detail about wetland values or (ii) area of wetlands or information that enabled wetland area estimation.

The final database consisted of 45 papers, of which 52% were from peer reviewed publications. The non-peer reviewed publications were reports (e.g., Leschine et al. 1997; Schuijt 2002), a working paper (Meyerhoff and Dehnhardt 2004) and a technical report (Emerton 2005). Five papers were split into multiple entries since they reported multiple study locations across 10 countries. Based on this set of 45 studies, we recorded geographic locations, study coordinates (if not reported, Google Earth was used to identify the coordinates), study year(s) (if study year was not reported the publication year was used), wetland area, the method used to value ecosystem services, the ecosystem services measured, and quantifiable effects of wetlands and their economic value when provided. We focused on regulating and provisioning ecosystem services and converted all wetland values to US dollars using the respective country’s exchange rate to the US$ at the time the study was conducted. Then, we multiplied the wetland values by the ratio of the 2018 consumer price index to the consumer price index of the year the study was conducted to convert all values to US$2018/ha/year.

Carbon sequestration was estimated in tonnes CO2/ha, and sequestration potential was then compared to values as determined by Canu et al. (2015). Local economic values (or geographically and economically similar ones) were used to determine the local monetary value of carbon sequestration. Since we measured possible benefits from carbon sequestration, we acknowledge that these are upper bound values and would need to be offset by variable production of greenhouse gases. For instance, converting wetlands to cropland may produce even more greenhouse gases (depending on the production system). We also did not include peatlands in the study as we focused on agricultural lands. We did not report emissions in each study location as we used sequestration data calculated by the original study.

Wetland water storage was estimated by the storage capacity (m3) of water/ha. In some studies, the total surface area was provided, and the volume was calculated from the area and average depth if reported in the paper. If a monetary value for water storage was not provided, then global averages reported in De Groot et al. (2012) were used.

Nitrogen filtration was predominantly reported in North America, or regions with similar economic and environmental conditions. As such, the ability of wetlands to filter nitrogen was estimated in kg N/ha of wetland, and the monetary value was estimated by averaging the values that had been provided and applying them to papers where an effect was provided but with no accompanying monetary estimate.

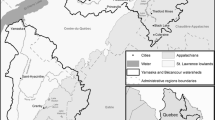
Provisioning services were valued by amalgamating services that included food, building materials, crafting materials, or firewood. Because of the considerable variation in the types of provisioning goods and services, the overall value of each material was converted into monetary terms (2018 US$/ha/year). Provisioning wetland ecosystem service studies were conducted mainly in developing countries (e.g., Africa; see Fig. 1), while regulating service studies were conducted mainly in developed countries, particularly North America (Fig. 1). See Appendix Table 8, in Appendix, for a list of the primary studies used in this study.

Fig. 1
figure 1

Location of study sites for the meta-analysis of provisioning (light grey triangles) and regulating (dark grey triangles) wetland ecosystem services values extracted from the literature

Full size image

Empirical model

Meta-regression involves the application of regression analysis to a pool of comparable empirical estimates (Nelson and Kennedy 2009; Richardson et al. 2015). We regressed the wetland values (US$2018/ha/year) extracted from our systematic literature review on a vector of covariates representing national wetland policies, economic indicators, biodiversity richness indicators, and study characteristics. The values included are categorized as provisioning and regulating wetland values. We did not include cultural and supporting wetland ecosystem values because we could not find enough data on them in our literature search to allow for model estimation.

We compared log–log and log-linear functional forms to estimate our meta-regression model. For the log–log, we took the logarithms of the dependent variable and continuous explanatory variables to improve model fit and reduce heteroscedasticity (Brander et al. 2013); we took only the logarithm of the dependent variable in the log-linear functional form. In the case of the log–log functional form, the coefficients of explanatory variables are interpreted as elasticities, which show that for continuous explanatory variables a 1% change in the variable will result in more than a 1% change in the dependent variable (for elastic effect) or less than a 1% change in the dependent variable (for inelastic effect); the coefficients in the case of log-linear function form represent a unit change in the dependent variable for a percentage change in the independent variables. When the regressor is a binary variable, the effect is compared to its reference group.

Since multiple observations were reported for some of the studies, we initially developed a mixed effects model to explain variation in wetland values. A general specification of a mixed effects model (with study included as a random effect) is given in Eq. 1:

$$Y_{i} = X\beta + u_{j} + \varepsilon_{i}$$
(1)

where: i = subscript i represents the ith observation. j   = subscript j represents the jth study. \(Y_{i}\) = dependent variable representing the logarithm of the value of wetland ecosystem service (US$/ha/year). \(X\) = vector of independent variables (including wetland policy variables, human population and economic indicators, and biodiversity richness indicators) and a constant term. \(\beta\)  = vector corresponding parameters of X to be estimated. \(u_{j}\) = stochastic error term for the jth study, which is assumed to be normally distributed with mean 0 and a variance \(\left( { \sigma^{2}_{u} } \right)\). \(\varepsilon_{i}\)  = stochastic error term for the ith observation, which is assumed to be normally distributed with mean 0 and a variance \(\left( {\sigma^{2} I} \right)\).

We used a likelihood ratio statistic to test for the appropriateness of the mixed effect model (Dias and Belcher 2015); an ordinary least squares model with fixed parameters is estimated if the mixed effects model is rejected. Two separate provisioning and regulating models with the same functional form as Eq. (1) are estimated using frequentist estimation procedure, with the “LMER” and “LM” R statistical software packages, for the mixed and fixed effects models, respectively. The dependent variable for the provisioning model was the logarithm of the total value of provisioning ecosystem services, while the dependent variable for the regulating model was the logarithm of the total value of regulating ecosystem services. The sample sizes for the provisioning and regulating models were 27 and 22, respectively, and we tested for heteroscedasticity using the Breusch Pagan test and multicollinearity using the variance inflation factor. A heteroscedastic model means the variance of the observation level error term is non-constant which would cause inferences from our model to be unreliable. Multicollinearity would reduce the efficiency of parameter estimates and undermine their statistical significance; however, it does not affect the reliability of parameter estimates. A variable inflation factor < 10 signifies that an explanatory variable is not a source of multicollinearity.

Benefit transfer estimation

The final functional model had the lowest root mean square error (RMSE) and mean absolute error (MAE) prediction error metrics. We used a tenfold cross validation procedure to estimate the prediction error metrics. For the tenfold cross validation procedure, we (1) randomly divided the data into ten equal groups or folds, (2) chose one of the folds as holdout test data, and estimated the model with the remaining nine groups of the dataset (k−1 folds); the prediction error metrics were estimated with the holdout test data, (3) repeated the process ten times, using a different set of holdout test data each time, and finally (4) used the average of the estimated prediction error metrics (RMSE and MAE) from each iteration of the ten-fold cross-validation procedure as the final statistic. The prediction errors from the estimated models are called meta-regression benefit function transfer errors. The meta-regression benefit transfer errors were compared with mean unit value transfer errors to show their potential for benefit transfer applications where wetland values were predicted outside this study. For the mean unit value transfer error, we estimated the prediction metrics by comparing the predictions from the models with the mean of the dependent variable. A flow chart summarizing how we conducted the meta-regression analysis on wetland ecosystem values is presented in Fig. 2 below.

Fig. 2
figure 2

Wetland ecosystem service value evaluation flowchart

Full size image

Description of variables and effects on wetland ecosystem services economic variables

Human population density was expected to have a positive impact on both regulating and provisioning wetland values (Brander et al. 2013). To calculate human population density, we used a global gridded human population layer (1-km resolution) that modeled distribution of the human population using counts and densities in 2015 (Center for International Earth Science Information Network 2017) and extracted the relative population density for each study location using bilinear interpolation with ArcGIS 10.5. Six study locations provided no data as the coordinates overlapped ‘no data' cells. For these, we calculated human population density by extracting the nearest density available to that point.

The income level of a country was expected to have a positive effect on both provisioning and regulating wetland values (Brundtland 1987; Brander et al. 2006; De Groot et al. 2012; Peimer et al. 2017) since higher levels of wealth are positively correlated with social willingness-to-pay. From the income level variable, we created a high-income binary variable which was given a value 1 if the gross national income (GNI) in current 2019 USD was greater than $12,535 and 0 if it was less (Serajuddin and Hamadeh 2021).

Agricultural total factor productivity is the average value of crops and livestock produced in relation to the total cost of inputs (land, labor, capital, and material resources) used in their production; we captured agricultural total factor productivity with the agricultural total factor productivity index (AgTFP) that measured the “average productivity of all the factors used in the production of agricultural commodities” (Economic Research Service 2019). The reference period of the AgTFP is 2015 (AgTFP = 100) such that AgTFP value of 120 in 2016 shows that over the 1-year, AgTFP has increased by 20%. Higher values of AgTFP would mean a more efficient agricultural production system which might need less resources (including agricultural lands) to produce agricultural commodities compared to the status quo (International Food Policy Research Institute 2018). Therefore, agricultural productivity was predicted to have a positive effect on wetland ecosystem values (provisioning and regulating).

Biodiversity variables

While wetlands are important habitats for many plant and animal species (Davies et al. 2008), studies that reported a biodiversity metric did not provide information to enable a standardized link to a monetary-value estimate. This is a common challenge in the empirical literature as biodiversity is generally viewed as having a positive cultural and social value, but not generally monetarized or monetization is often incomplete due to lack of data or knowledge (Nunes et al. 2001).

To calculate an index to represent biodiversity we compiled the global species richness of birds from species range maps (≈ 28 × 28 km) by Birdlife International (http://www.birdlife.org/). The global species richness of amphibians (≈ 1 × 1 km) was compiled by the International Union for the Conservation of Nature (IUCN) and the Columbia University Center for International Earth Science Information Network (CIESCN) (IUCN and CIESCN ). Study locations were overlaid with global species richness grids to calculate the total species richness at each site using bilinear interpolation with ArcGIS 10.5. Species richness (birds and amphibians) is expected to have positive effects on wetland values (provisioning and regulating).

National wetland policy

No-net-loss wetland policy, deployed in several jurisdictions, seeks to maintain the total area of wetlands via wetland reclamation, mitigation, and restoration efforts when a wetland is converted to another land use. This policy is expected to help conserve wetlands, and hence increase their benefits to society. This binary variable was 1 if a country has this policy in place and 0 otherwise. Similarly, binary variables for national ecosystem policy, use of incentives and use of penalties to conserve wetlands, are expected to have positive impacts on wetland conservation, and therefore wetland values. Country-specific policy information was obtained from Peimer et al. (2017). There may be regional differences in wetland polices within the same country; for instance, some provinces in Canada have a no net loss policy whereas others do not. However, for this study we focused on overall country-level wetland policies.

Study characteristics

Study-specific nuances or characteristics may influence the heterogeneity in wetland values (both regulating and provisioning). Study-specific variables included wetland area, peer-review journal publication status, valuation method, and geographic location (latitude and longitude). These variables are routinely added to meta-analyses (Brander et al. 2013). Wetland area, a continuous variable, is the size of the wetland that is being evaluated in a specific study. We expected wetland size to have a negative effect on wetland values, since people may be willing to pay the same for a small subset of an environmental feature as for a large area (Loomis et al. 1993). However, Reynaud and Lanzanova (2017) showed that larger lakes are more valued than smaller lakes, because some ecosystem services require a minimum threshold of wetland area (Brander et al. 2013). The valuation method uses a dummy variable which equals 1 if the valuation methodology is an economic valuation method and 0 otherwise. Economic valuation methods are listed in Woodward and Wui (2001) and Brander et al. (2006) and include production functions, replacement cost, and contingent valuation. Peer reviewed studies is included as a binary variable which takes on a value 1 if study is peer reviewed and 0 otherwise. We expect peer review to have a positive effect on wetland values (Ghermandi and Nunes 2013; Reynaud and Lanzanova 2017) as we assumed researchers may be more encouraged to publish studies that produce more significant wetland values. The variable descriptions and their expected effects on wetland values are summarized in Table 1.

Table 1 Descriptions of variables used in the meta-analysis and expected effects on wetland values
Full size table

Results

In this section we present the summary statistics of the variables that are used in estimating the regulating and provisioning meta-regression models. We also present the estimated meta-regression model results and show how our estimated meta-regression models can be used to estimate provisioning and regulating wetland values for other wetlands globally.

Summary trends

The estimated mean value for wetland-based provisioning ecosystem services was US$1645/ha/year (in 2018 US$) with a standard deviation of USD$3,168/ha/year, indicating high variation in ecosystem service values across studies (Table 2). The estimated mean value for wetland-based regulating ecosystem services was US$8711/ha/year with a standard deviation of US$22,375/ha/year. The mean and standard deviation of wetland area for the provisioning meta-regression model were 870,000 and 2,800,000 ha, respectively. Similarly, the mean and standard deviation of wetland area for the regulating meta-regression model were 2,730,000 and 6,600,000 ha, respectively. This shows that wetlands in the regulating meta-regression model, on average, were relatively larger than in the provisioning model. About 70% of the wetlands in the provisioning model were valued using an economic valuation method compared to 52% for the regulating model. The other non-economic valuation method was mainly ecological modeling where the ecosystem end points of wetlands were identified, and their values estimated using corresponding monetary values reported in the literature (see Canu et al. 2015 and De Groot et al. 2012).

Table 2 Summary statistics for variables in the modelling of provisioning and regulating values of wetlands
Full size table

In terms of the economic variables, the mean agricultural total factor productivity index in both models was 114; however, the heterogeneity in the values was greater in the regulating model. Considerably more studies conducted in high-income countries were included in the regulating model (70%) than in the provisioning model (37%). Conversely, about 22% of the studies in the provisioning model were conducted in low-income countries versus 9% in the regulating model. Also, the mean (1003 humans/km2) and standard deviation (2467 human population/km2) of population density were greater for the study regions in the regulating model than for wetlands in the provisioning model with a mean of 755 population/km2 and standard deviation human of 2223 population/km2.

More jurisdictions in the regulating model had an identified wetland policy for conserving wetland ecosystem services (15% more), used an incentive-based policy to conserve wetlands (11% more), used penalties to conserve wetlands (33% more) or had a no-net-loss wetland policy (15% more) than jurisdictions in the provisioning model (Table 2). This suggests that wetlands in the regulating model were supported by a more comprehensive conservation policy framework.

There were more amphibians associated on average with wetlands in the provisioning model (16.2 species/ha), and more heterogeneity in the values of the variable (standard deviation of 10.6 species/ha) than in the regulating model with a mean (standard deviation) species/ha of 12.39 (9.3). There were also more bird species associated with wetlands in the provisioning model (283/ha) than wetlands in the regulating model (194/ha) (Table 2).

Meta-regression results

In this section we discuss the factors that influence regulating and provisioning ecosystem services on agricultural landscapes. First, we discuss the results of the provisioning model followed by the results of the regulating model. The likelihood ratio test statistics of 0.52 (p-value = 0.47) and 0.12 (p-value = 0.73) indicated that a mixed model (using study as a random term) was not supported for the provisioning or regulating model structures, respectively. Therefore, the results of the fixed effect models for both categories of wetland ecosystem services are reported in this section.

Provisioning meta-regression model

We chose a restricted log-linear (Table 3) model as it produced the lowest meta-regression errors compared to the log–log model. The log-linear model was restricted because we dropped the variables that were highly correlated (r > 0.6) with other variables or were consistently not significant even at the 10% level for all the estimated models (this was necessary because of our small dataset). For this model, we dropped the variable representing economic valuation method since it was correlated with high-income (r = 0.68). We also dropped no-net-loss wetland policy, use of incentives, and use of penalties in wetland policy because they were consistently not significant across all the estimated models. Overall, the final model was significant (F statistic = 5.88, p-value = 0.0009) and explained 65.3% of the variation in the dependent variable (log of provisioning wetland ecosystem values). The model was homoscedastic, with the variance of the error term being constant (Breusch Pagan statistic = 5.26, p-value = 0.87); multicollinearity was not detected since all explanatory variables had variance inflation factors < 10.

Table 3 Provisioning meta-regression model results
Full size table

Population density and high-income both had positive effects on the provisioning wetland values on agricultural landscapes, which were significant at the 10 and 5% levels, respectively (Table 3). The estimated coefficient of human population density means that a 1% increase in density will result in a $0.0004/ha/year increase in the value of wetland provisioning services on agricultural landscapes; similarly, wetlands located in a high-income country would have about $3.59/ha/year greater provisioning value than those located in countries from other income groups. Agricultural total factor productivity index had a negative effect on the value of wetland provisioning services on agricultural landscapes (significant at 10% level); specifically, a 1% increase in agricultural factor productivity would result in a $0.027/ha/year reduction in the value of wetland provisioning services. The value of wetland provisioning services reported in peer-reviewed journal publications was about $3.49/ha/year more than values in other studies (significant at 1% level). Other variables in this model were found to be not significant including ecosystem service goal (p-value = 0.57), longitude (p-value = 0.26), latitude (p-value = 0.31), bird species richness (p-value = 0.11), wetland area (p-value = 0.66), and amphibian species richness (p-value = 0.56). Our meta-regression models could estimate the values of wetlands on agricultural landscapes with lower prediction or transfer errors (71 and 66% for root mean squared and mean absolute deviation statistics, respectively) compared to the unit value method, which uses average $/hectare values to value wetlands.

Regulating meta-regression model

For the meta-regression model representing regulating wetland ecosystem services in agricultural landscapes, we selected the restricted log–log model because it produced the lowest meta-regression errors. Like the restricted provisioning model, we dropped variables that had high correlation coefficients (r >|0.6|) with other explanatory variables. For instance, we dropped use of incentives and peer-review because they were correlated with ecosystem service goal (r = 0.69) and economic valuation method (r = − 0.70), respectively. Several variables including no-net-loss wetland policy, use-incentives wetland policy, use-penalties wetland policy, peer-reviewed journal publications and bird richness were dropped from the final model because they were not significant across all the estimated models.

Overall, the final model was significant (F statistic = 9.23, p-value = 0.0002) and explained about 78% of the variation in the value of wetland regulating services on agricultural landscapes. The model was homoscedastic, which means the variance of the error term was constant (Breusch Pagan statistic = 9.07, p-value = 0.43). Variance inflation factors for all explanatory variables were < 10, indicating a lack of multicollinearity.

The model results showed that a 1% increase in wetland area resulted in a 0.31% decrease in the value of regulating wetland ecosystem services on agricultural landscapes (p = 0.012) (Table 4). A 1% increase in agricultural total factor productivity index produced a 7.3% increase in the value of wetland regulating services (p = 0.03). The value of wetland regulating services located in high-income areas were approximately 3.6% higher than similar wetlands located in jurisdictions with lower income (p-value = 0.04). The latitude coordinate had a positive effect with a magnitude of 0.054 (p-value = 0.06). All other variables (population density, economic valuation method, longitude, amphibians, ecosystem service goal) were not significant, even at the 10% level. The meta-regression benefit transfer errors were found to be 300 and 185% lower (for root mean square and mean absolute error statistics, respectively) than the mean unit value transfer errors; this means the estimated meta-regression models could estimate the values of new wetland values on agricultural landscapes at significantly lower errors than the unit value method (Table 4).

Table 4 Regulating meta-regression model results
Full size table

Wetland application of estimated meta-regression models

We applied the final provisioning and regulating models to estimate wetland values for selected wetlands on agricultural landscapes across the world (Table 9 in Appendix). We predicted the wetland value and the 95% confidence interval for each wetland area listed in Tables 5 and 6 by assigning values to the independent variables in the model, for example, by including wetland policy variables, human population and economic indicators, and biodiversity richness indicators, that are appropriate for the wetland and the country location (see Tables 10 and 11 in Appendix for details and a few examples of how we predicted the wetland values). Apart from the Buckingham Marshes, the information on the other wetlands, including country-specific information, were included in the meta-data that was used to estimate the regulation model. Similarly, except Murray-Darling Basin and Pantanal, information on the other wetlands was new to the estimated provisioning model. Predicting the wetland values using information new to the estimated models can help us to assess the robustness or how well our estimated models will perform for real-world policy applications.

Table 5 Model-predicted wetland ecosystem values in agricultural landscapes
Full size table
Table 6 Summary statistics of ecosystem service values in meta-regression meta-data
Full size table

The model-predicted regulating value for the Buckingham Marshes in UK is significantly higher ($11,216) compared to wetlands located in other high-income countries such as US ($214) and New Zealand ($0.62; Table 5). In contrast, the model-predicted regulating value of wetlands in lower-income countries are significantly lower (Sri Lanka = $1.47; Malawi = $0.74). Also, the average model-predicted regulating values for high income countries ($11,430; Table 5) is about $1,000 lower than the average of the original regulating values reported in the regulating model meta-data for high-income countries ($12,500; Table 6); similarly, the average model-predicted regulating value for low-income countries is about $1.5 lower than the average regulating value for wetlands located in low income in the model’s meta-data.

The provisioning value of wetlands located in high-income countries, Germany, Australia, and Canada, are significantly greater ($117–2122) than the provisioning values of wetlands in middle- and low-income countries (e.g., Brazil = $0.95, Kenya = $80; Table 5). Moreover, the average model-predicted provisioning ecosystem service value for high-income ($2633; Table 5) and non-high-income ($36; Table 5) countries are about $1,000 lower and $530 lower than the average value of the original provisioning service values reported in the provisioning model meta-data for high-income ($3596; Table 6) and non-high-income countries ($568; Table 6), respectively.

Discussion and policy implications

Wetlands are highly valued because they produce services that are useful and beneficial to humans (Mitsch and Gosselink 2000). Therefore, the positive effect of increasing human population density on wetland values (both provisioning and regulating ecosystem services) is expected and is consistent with previous studies (Mitsch and Gosselink 2000; Brander et al. 2006, 2013). It is understandable that with greater human populations living near wetland areas a greater number of people could benefit from local wetland services with improved access to the wetland areas. Our analysis focused on wetlands located within agricultural landscapes with these areas characterized as having relatively large human populations when located close to urban developments but with lower human populations in more rural landscapes.

We found that wetlands in high-income countries have higher provisioning and regulating ecosystem service values compared to those in other income groups. Most citizens in wealthy countries live above global average subsistence levels and thus are more likely to have a higher capacity and willingness to pay for the support or be involved in protecting ecosystems, including wetlands (Mitsch and Gosselink 2000).

We showed that agricultural total factor productivity index (AgTFP) has a positive impact on wetland regulating values and a negative effect on wetland provisioning values. A positive change in AgTFP implies a more efficient agricultural production system where relatively less inputs (including agricultural land) are required to produce equivalent agricultural outputs than in the pre-existing AgTFP state (International Food Policy Research Institute 2018). As AgTFP increases, there is perhaps less pressure for agricultural land expansion (including wetland conversion) to produce agricultural commodities; in this case wetland functions would have more time to evolve to produce ecosystem services to benefit society. However, the negative effect of AgTFP on wetland provisioning service values is contrary to expectation. It could be that relatively fewer countries (37%) in the provisioning model are in the high-income status compared to 70% for the regulating model; people in developing nations are relatively poor so might see the need to convert wetlands to croplands to satisfy their subsistence needs, even in the face of increasing agricultural total factor productivity. Also, in high income countries agriculture tends to be more technologically advanced and specialized, as result these agricultural zones may ascribe lower values to provisioning services as these services may not be perceived as necessary for land productivity.

Wetland regulating and provisioning values tend to be negatively related to wetland area (even though the effect on provisioning service value is not significant at the 10% level). The negative relation between wetland area and regulating service value was also reported by Brander et al. (2013). People may be willing to pay for a representative wetland in a given landscape, but they do not express proportionally larger values for larger areas of wetland, that is a small subset of an environmental feature but not for a large area (Loomis et al. 1993). However, a potential positive relationship may exist between wetland area and values because wetland values may require a minimum threshold of area (Brander et al. 2013; Reynaud and Lanzanova 2017).

Studies that are published in peer-reviewed journals are positively related to provisioning wetland values, suggesting a potential publication bias such that studies with significant results on wetland values are more likely to be published than those with less encouraging results. An implication of publication bias is that caution is needed when generalizing results to all provisioning wetland values (Sutton et al. 2000). This observation has been reported previously (Ghermandi and Nunes 2013; Reynaud and Lanzanova 2017). Our study shows that the presence of a national wetland policy could have a positive impact on provisioning wetland values, but a negative impact on regulating wetland values (even though the variable is not significant, even at the 10% level in both cases).

The results from our study can help inform the application of benefit transfer methodology to generate more representative values for target wetland sites for specific wetland ecosystem services. Although unit benefit transfer is the easiest and cheapest valuation method, it may produce unreliable transfers because the demographic and environmental resource location characteristics of the past studies and target sites may be significantly different (Navrud and Ready 2007). Our meta-regression value functions generate lower prediction errors than do unit value benefit transfer methods. Traditionally, unit value benefit transfer approaches simply used mean values from relatively comparable wetland study sites to represent values for the target site. Meta-regression benefit transfer, which uses rigorous quantitative methods to analyze multiple environmental resource values from empirical studies, accounts for demographic and environmental resource location characteristics of past studies; therefore, they may produce lower benefit transfer errors when the results are extrapolated to estimate environmental resource values at policy sites.

Our study applies a meta-regression model to tailor those values from comparable wetland study sites to more effectively develop values that represent the biophysical, social, and economic context of the study wetlands. In a review of 38 meta-regression valuation studies, Rosenberger (2015) reports that the average absolute percentage error (APE) for meta-regression and mean unit value transfers are 65 and 140%, respectively. Also, in a meta-analysis study to estimate the effect of waste sites on residential property values, Schutt (2021) reports a mean APE meta-regression error ranging from 133 to 684%. Our estimated mean meta-regression APE and mean value APE were 200 and 385%, respectively (for the regulating meta-regression model) and 168 and 234%, respectively (for the provisioning model), which are consistent with Schutt (2021). In contrast, our estimated benefit transfer errors are considerably greater compared to the average transfer errors in the literature (Rosenberger 2015). This may be due to the lack of sufficient data (n = 23 for the regulating model and n = 27 for the provisioning model) to allow us to efficiently estimate a global meta-regression value function to value wetlands on globally heterogeneous agricultural landscapes. However, our general observation that meta-regression transfer errors are significantly lower than mean transfer errors is consistent with the literature on benefit transfer errors.

In the absence of localized studies to value wetlands, our models could be used to relate wetland values on agricultural landscapes with our benefit transfer tool (compared to the mean unit value transfer approach) and aid in land-use planning and wetland conservation policy development. For instance, we applied our estimated meta-regression models to estimate wetland regulating values and predicted the values of wetlands on agricultural landscapes ($/Ha/Year) in the Buckingham marshes in UK ($11,216), Rainwater basin in US ($214), and Whangamarino in New Zealand ($0.62); the mean model-predicted regulating values for the high income countries ($11,430) is about $1000 lower than the average of the original regulating values reported in the regulating model meta-data for high-income countries ($12,500). Also, we model-predicted the regulating wetland values for the Kala Oya Basin ($1.47) in Sri Lankan and Lake Chilwa in Malawi ($0.74), both located in low-income countries; the mean model-predicted regulating service values for the low-income countries is $1.83, which is about $1.5 lower than the mean regulating value reported in the original meta-data used to estimate the regulating model. The variability in the predicted wetland regulating values can be explained by the differences in wetland area, country income status, agricultural total factor productivity index and position of wetlands. In comparison, Brander et al. (2013) estimated the mean regulating values for high income regions (US: $1490, Oceania: $512 and Western Europe: $2353) to be $4013/ha/year which is lower than our mean model predicted regulating values for high income countries of $11,430. They also reported the mean of regulating wetland values for south Asia ($5956) and East Africa ($983) to be $3961, which is significantly higher than our mean model-predicted regulating value for low-income countries of $1.84. These differences could be explained by the differences in the variables that best explained the regulating meta-regression models and the levels of variables that were included in both studies. For example, agricultural total factor productivity and high income are among the key variables that were important to our estimated regulating model but not included in Brander et al. (2013), and the levels of wetland areas that were used to predict the values were in the millions of hectares for Brander et al. (2013), while the levels in our model were in the thousands. The large 96% prediction interval for our model, which was also observed in Brander et al. (2013), suggests that our predicted values must be predicted with caution; however, the meta-regression transfer method provides a better alternative to valuing local wetlands compared to the unit value transfer since its transfer error or prediction error is considerably lower.

We also predicted the provisioning wetland values for wetlands in Eastern Saskatchewan in Canada ($2122), the Elver River Basin in Germany ($117), the Murray-Darling Basin in Australia ($1183), the Pantanal in Brazil ($0.95), wetlands in southeast Asia ($8.74), and the Yala Watershed in Kenya ($80). The mean of the model-predicted provisioning service value for high-income ($2633) and non-high-income countries (Brazil, southeast Asia and Kenya; $36), were about $1000 and $530 lower (for high and non-high-income countries respectively) than the mean provisioning service values in the original meta-data used to estimate the provisioning model. The differences in the predicted wetland provisioning values could be due to the differences in income status, agricultural total factor productivity and population density for the countries where the wetlands are located. Again, the results of the predicted provisioning values must be interpreted with caution because of the large 95% prediction interval for the predicted values. Tables 10 and 11 provides examples of how we predicted wetland values, and how wetland resource managers could use it as a guide to estimate local wetland values.

Conclusion

As there is increasing pressure on wetlands in agricultural landscapes due to the intensification and expansion of agricultural production and the conversion of wetlands for urban and industrial development there is a greater demand for policies and programs to mitigate these wetland loss trends. Wetland conservation policy can be supported with a more complete understanding of the social values of wetlands and the ecosystem services that they provide to society. However, site specific representative values of wetland ecosystem services on agricultural landscapes are difficult and expensive to estimate. Benefit transfer methodology has been applied to enable a more rapid and cost-effective approach to assign values to wetlands and the ecosystem services they provide. However, a barrier to developing representative wetland ecosystem service values through benefit transfer is a lack of understanding of the biophysical, social and economic contexts as well as the suite of wetland ecosystem services provided by the source valuation site and the study site.

Our study indicated key variables to inform the effective implementation of a benefit transfer procedure to value wetlands are agricultural total factor productivity index, the income level of a country, and the wetland area under study for the regulating model, and income level of a country, peer-reviewed journal articles, agricultural total factor productivity index, latitude, and population density for the provisioning model. For instance, the results can be used to help calculate the total value of wetlands in areas where localized studies are not available. Wetland managers generally consider the regional context of target wetlands, and we would recommend using the estimated meta-regression value functions to help develop estimates of local wetland values by selecting landscape appropriate levels of key independent variables in an analysis.

Moreover, the results from our study could be used to support the development of more reliable and representative wetland values using a benefit transfer approach compared to those values estimated through a unit value transfer method, especially in the absence of original valuation studies. This is based on the findings that the prediction errors from our models, compared to those from mean-value unit transfers, were lower than similar estimates reported in the literature. For instance, our estimated provisioning and regulating meta-regression models could estimate local wetland values on agricultural landscapes at considerably lower prediction or benefit transfer errors (66 and 185% absolute percentage errors, respectively) compared to unit value transfer errors from both models. This would enable planners to implement better informed wetland conservation policies and can assist in the estimation of the tradeoffs of wetland conversion or conservation on agricultural lands.

While the studies used for this analysis were mostly based on study areas located in developed countries, this is still useful in the context where there are significant pressures to convert wetlands to the production of agricultural commodities. Future studies in developing countries would enable a more accurate benefit transfer of wetland ecosystem-service valuations. In the meantime, our benefit transfer study can be useful to support localized calculations to make policies that consider the total ecosystem services that wetlands provide and integrate them into land-use planning. Moreover, future studies are encouraged to value cultural and supporting wetland ecosystem services which were lacking in our literature search; therefore, we could not include the value of supporting and cultural ecosystem services in our meta-regression model estimations. Lack of sufficient studies on these services could undermine their role in benefit cost analysis of wetland conservation policies.