1 Introduction

In the last century, industrialization and population growth have also increased environmental pollution. In addition to wastes such as metals and dyes used in many production processes, human-caused drug metabolites, pesticides, or wastes generated after use have reached a level that threatens the environment and human health. Among these pollutants, metals occupy the largest area. Mercury, one of these metals, is used in many industrial areas, as well as in areas such as cosmetics and electronics, and it pollutes environmental waters from natural sources.

Mercury is a very dangerous metal for human health. The common types of mercury, which exist in three forms, are Hg (0), Hg (I) and Hg (II). Especially the Hg (II) form is known to cause many diseases (Chalkidis et al., 2020). When it enters the human body by inhalation and ingestion, it can lead to failure and even death in many organs, especially the nervous system and kidneys (Ochedi et al., 2020). Neurological effects are seen even at doses of 0.5 mg/kg. At this dose, it causes inhibition of brain development and regression in the development of psychomotor movements, especially in fetuses. The daily intake dose should not exceed 0.1 µgKg−1 day−1, especially in lactating and pregnant women (Berlin et al., 2007). Due to the enrichment of seawater, the removal of mercury in the form of methylmercury from fish is very important in this respect.

There are many chemical and biological treatment methods for the removal of mercury from the aqueous environment. Filtration (Xiang et al., 2022), oxidation (Guan et al., 2021; Liu et al., 2020), biological treatment (Rani et al., 2021), and adsorption (Eissa et al., 2023; Li et al., 2021; Şimşek & Ulusoy, 2016; Zhang et al., 2019) are widely used methods for the removal and recovery of metals from aqueous solutions. However many of these methods are economically expensive and require technology. Among these methods, adsorption is a preferred one as it is both economical and sustainable, as well as easy to design. At the same time, the fact that it can be used even in very small concentrations has led to an increase in the number of studies in the field of adsorption for mercury removal in recent years.

The adsorption process is widely used, especially in metal removal studies (Cheira, 2020). It is possible to design an appropriate adsorbent with an interface design that will allow metals to be taken to the solid surface by using several chemical interactions such as chelate/complex/ion exchange. Considering the hard-soft acid–base (HSBA) approach (Chattaraj et al., 1991), adsorbents containing functional groups on the adsorbent surface with which mercury can interact can be used effectively in mercury adsorption. Among commonly used adsorbents, carbon, clays, zeolites, minerals, and natural and synthetic polymers are often preferred. In particular, natural adsorbents are preferred because of their high surface areas, functional groups, easy availability, and economy.

Walnut Green Husk (WGH) is an agricultural waste that occurs as waste in walnut production, has very little use, is largely thrown into the environment, and causes environmental pollution. It consists largely of 5-hydroxy-1,4-naphthoquinone, a brown pigment called juglone. In addition, it contains many flavonoids such as tannic acid, ellagic acid, naphthoquinones, and naphthalenone types, as well as glycosides and hydroxycinnamic acids (Jahanban-Esfahlan et al., 2019). The insoluble part of WGH, which is approximately 50% water-soluble by weight, contains cellulose. Many of the substances mentioned in the soluble part it contains are substances that can form a potential complex for metals with groups such as -OH, -OCH3, and carbonyl they carry (Fernández-Agulló et al., 2013). However, it is not possible to use the soluble part as an adsorbent. If this soluble fraction is taken as a solid phase or trapped or grafted in a polymer structure, it can be used as an effective adsorbent. Although there are studies on the use of waste walnut shells as an adsorbent, studies on WGH are very few. In this respect, the use of waste material from the removal of another waste, mercury ions, becomes more important in terms of the "two birds with one stone" strategy.

Polyacrylamide hydrogel is known for its inertness and high water-holding capacity. In particular, previous studies have shown that adsorbents formed by incorporating chelate-compact forming materials, which are water-soluble and have a high metal affinity, into the hydrogel structure, have been used effectively (Ulusoy & Şimşek, 2013).

Immobilization of natural or synthetic ligands with high metal affinity and substances that are chelating but cannot be used as adsorbents due to their solubility by grafting, blending, or impregnating them into a matrix structure or a polymer is an effective way to synthesize potential new adsorbents (Qi et al., 2021). In particular, converting these structures of plant-origin non-wood into an adsorbent is important both in terms of the environment and the synthesis of an effective adsorbent (Fan et al., 2019; Wang et al., 2019). WGH is an agricultural waste rich in these structures, which is easily soluble in water and known to interact with metals.

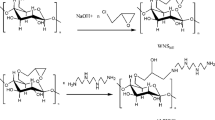
In this study, the water-soluble part of WGH, namely extract (EWGH) and polyacrylamide (Paa), was used during polymerization, and the use of the new material (EWGH@Paa) formed for mercury adsorption was investigated (Fig. 1.). The characterization of the newly obtained material was clarified by Fouirer Transform Infrared Spektrofotometre (FTIR) and Scanning electron microscopy (SEM), and the surface properties were clarified by the point zero charge (PZC) method. The adsorption of the material was tested for Hg (II) ions, and the effect of various conditions on the adsorption was investigated. The results showed that the synthesized new material will be used as a very high-capacity and fast adsorbent for mercury.

Fig. 1
figure 1

Illustration of process

Full size image

2 Chemicals

The chemicals used in the study as Acrylamide monomer (aa), Ammonium peroxide disulfate (APDS), N, N’- methylene bisacrylamide, N, N, N, N tetramethylene diamine (TEMED), Hg(CH3COO)2 HCl, NaOH, KNO3, HNO3, C2H5OH, and other chemicals were obtained from Merck (Germany). The chemical structures of using chemicals are given in Fig. 2. All used chemicals were at analytical reagent grade. Double-deionized water was used throughout the experiments and all experiments were performed in duplicates.

Fig. 2
figure 2

Chemical structure of using chemicals

Full size image

3 Preparation of Adsorbent

4 g of dried WGH dissolved in water. 2 g of soluble WGH mixed to 4 g AA 0,8 g as cross-linker, N, N- methylene bisacrylamide over 2 h. It was polymerized by adding APDS and TEMED. Washed several times with deionized water. The composite sample was dried at 40 0C, ground, sieved to a particle size smaller than 1 mm, and stored in a polypropylene container.

4 Adsorption Study

Adsorptive features of the new biosorbent were investigated for Hg (II) ions. For this purpose, 0.05 g of the adsorbent was equilibrated with 10 mL of Hg (II) in the concentration range of (0.25 – 7.5) × 10–3 mol L−1. The adsorbent–solution systems were equilibrated for 24 h at 298 K in a thermostatic water bath and equilibrium solutions aqueous phase were obtained by centrifuging at 2.500 rpm for 5 min.

The concentration of Hg (II) was measured by using the PAR method as spectrophotometrically. In this method, Mercury formed a selective complex with PAR (4-(2-pyridylazo) resorcinol) at pH 8.5. 7 × 10–3 mol L−1 of PAR was prepared in Tris/HCl buffer. A fraction of supernatant, 500 μL, was added onto 2.5 mL of the reagent, and the absorbance of the formed complex was measured at 507 nm.

5 Results and Discussions

5.1 FTIR Analysis

The FTIR spectra of the soluble WGH, PAA, and composite used in the adsorption study are given in the “Supplementary Material” and the FTIR spectra after the adsorption of the synthesized composite adsorbent and mercury are shown in Fig. 3. The regions between 1200 cm−1 and 1600 cm−1 in the spectrum are the peaks of the -COOH, C–C, C-H, and -OH vibration frequencies in the WGH structure (Torre et al., 2021; Wang et al., 2023).

Fig. 3
figure 3

FTIR spectra of EWGH@Paa and Hg (II) adsorbed EWGH@Paa

Full size image

As shown in the spectrum, deformation, and changes in peak intensities were observed in the peaks in the 1310 -1535 cm−1 region after mercury adsorption. The peak disappearing after adsorption at 1535 cm−1 and the peak broadening after adsorption in the range of 1410–1446 cm−1 were evaluated as evidence of mercury adsorption. Based on the theoretical calculations given in the "Details of density functional theory calculations" section, it was concluded that juglone, ellagic acid, and sinapic acid, which are predominant in the structure of WGH, are the result of changes in the chemical environment due to interaction with mercury. This result can be explained by the change in stretching vibrations as a result of complex-ion exchange formed by WGH-based OH groups in the composite with mercury ions.

5.2 SEM and EDX Analysis

The before and after adsorption SEM images of the EWGH@Paa material used in the adsorption study and the after-adsorption EDX diagram are shown in Fig. 4–5. The SEM images show that a softer and smoother surface was formed after adsorption. Considering the adsorption capacity, it is understood that there is a change in the morphology of the surface after very high mercury adsorption. After adsorption, the decrease in prorosity on the surface and the formation of a smoother surface were evaluated as evidence that mercury binds to the ligands on the composite material that will form chelate-complexes with mercury (Allouche et al., 2014; Li et al., 2020). In the EDX diagram, the presence and high intensity of the Hg peak after adsorption support the experimental adsorption results.

Fig. 4
figure 4

SEM images of materials (a) EWGH (b) EWGH@Paa, (c) Hg (II) adsorbed EWGH@Paa

Full size image
Fig. 5
figure 5

EDX diagrams of Materials (a) EWGH (b) EWGH@Paa (c) Hg (II) adsorbed EWGH@Paa

Full size image

5.3 Surface Area and Pore Structure Analysis of EWGH@Paa

An adsorption–desorption study of N2 was carried out to determine the surface area and pore distribution of the adsorbent, and the isotherms are shown in the Fig. 6. The adsorption isotherm conforms to the Type I isotherm, which shows a microporous structure. This type of pore structure indicates that adsorption occurs through the adsorption of micropores. The BET surface area of the new material was 14.853 m2g-1, and the average pore size was found to be 2.91 nm. (Caner et al., 2015).

Fig. 6
figure 6

Nitrogen adsorption–desorption isotherms

Full size image

5.4 PZC evaluation of adsorbent

One of the effective parameters in adsorption is the surface charge of the adsorbent. Whether the solution is acidic or basic changes the surface charge of the adsorbent. The variation of the surface charge is a very important factor for adsorption when the charge of the adsorbed species is taken into account. For example, for cationic species such as metals, a positive surface reduces adsorption, while a negative surface causes an increase in adsorption. Therefore, it is important that the surface charge changes depending on the pH of the solution. In this pH, which is accepted as a point zero charge, the positive and negative charges are proportionally distributed equally and the total surface charge is accepted as zero. Generally, the region where the surface charge is zero can be found by measuring the pH after the interaction of the adsorbent, which interacts with solutions at different pHs under constant ionic strength (Bakatula et al., 2018). For this purpose, solutions between pH 2–12 were prepared in 0.1 molL−1 KNO3 solution. Solution pH adjustments were made using HCl and NaOH. Equilibrium pH was measured after 24 h and the results are given in Fig. 7. The results showed that the surface charge did not change significantly between 5–7. In this range, the average charge distribution is assumed to be balanced and the surface charge to be zero. Below this point, i.e. in acidic conditions, the surface charge is assumed to be predominantly positive and above it negative.

Fig. 7
figure 7

PZC Study of Adsorbent

Full size image

5.5 Effect of Solution pH on Adsorption

Solution pH, which is one of the factors affecting adsorption, is one of the important parameters, especially in metal adsorption studies. Because the change in the presence of H+ and OH− ions in the solution environment affects the metal ions species, as well as they can compete with these species and affect the adsorption. To determine the change of adsorption with pH, adsorption experiments were carried out at different pH from the constant Hg concentration and the results are given in Fig. 8. As can be seen, a decrease in adsorption was observed at low pH. An increase in adsorption was observed around pH 4, where the surface charge was measured as zero. No significant change in adsorption was observed at pHs above 4. The decrease in adsorption at low pH can be explained by two effects. Firstly, the competition between the increasing H+ ions and the cationic and dominant species of Hg (II) ions at low pH negatively affected the adsorption. Secondly, it can be explained by the change in the dominant mercury type with increasing solution pH. (Inbaraj et al., 2009; Kubáň et al., 2007). It is considered that Hg (II), which is dominant at low pH, is replaced by a neutral species, Hg(OH)2 and Hg(OH)+, and these species cause an increase in adsorption with the decrease in the cationic property of the surface. Adsorption studies were not carried out in alkaline conditions because adsorption and precipitation occur together with mercury hydroxides formed with increasing OH− concentration.

Fig. 8
figure 8

Influence of pH of solution to Hg (II) adsorption

Full size image

5.6 Effect of Mercury Concentration on Adsorption

Finding how adsorption changes with the concentration of the adsorbed species is important for the process. Parameters related to adsorption and adsorbent can be obtained by investigating the compatibility of the isotherms generated at different concentrations, while keeping other parameters constant, with adsorption models based on various mathematical equations. The Langmuir, Freundlich, Temkin, and Dubinin-Radushkevich models are commonly used among these models and were used in this study (Al-Ghouti & Da'ana, 2020). For this purpose, the adsorption of solutions containing mercury at different concentrations was performed, and the equilibrium mercury concentrations were determined using the methods given in Section “Adsorption study”. The isotherm plotted between Ce and Qe obtained experimentally and the graph showing the fit of the experimental results to the theoretical models are shown in Fig. 9, while the parameters obtained from the models are given in Table 1.

Fig. 9
figure 9

Adsorption isotherms and fitting curves of models

Full size image
Table 1 Adsorption parameters Hg (II) onto EWGH@Paa
Full size table

The adsorption isotherm obtained follows the L-type adsorption isotherm in the Giles classification; however, at low concentrations of mercury, it also shows high adsorption amounts that are typical of an H-type adsorption isotherm. In this type of adsorption behavior, adsorption continues until the adsorption sites become saturated. At low initial concentrations, adsorption occurred in the solid-phase direction, whereas at intermediate concentrations, a solid–liquid equilibrium was established. At high concentrations, the adsorption sites become saturated, and a plateau is reached.

The experimental data fit the Langmuir model, and the obtained adsorption capacity was 1.808 molKg−1 (362,67 mgg−1), which is a very high adsorption capacity. The soluble content of WGH, such as tannic acid, ellagic acid, juglones, naphthoquinone glycosides, and numerous flavonoids in the composite, has been effective in adsorption (Jahanban-Esfahlan et al., 2019). The strong interaction between these structures, which are grafted/entrapped in the inert hydrogel, and mercury ions supports the adsorption energy obtained from the D-R model. The adsorption energy, which evaluates whether the binding is chemical or not, was found to be 13.88 kJ mol-1, indicating that this binding is a chemical interaction. The β value obtained from the Freundlich model is also considered to be a measure of surface heterogeneity. Simultaneously, as this value approaches zero, the adsorption energy increases with increasing adsorbate concentration on the surface (Chen et al., 2022). The Freundlich isotherm is not suitable for providing information on surface saturation or adsorption capacity.

The Temkin model assumes that the binding energy is uniform and the adsorption heat is linear at moderate concentrations, considering the interaction between the adsorbate and adsorbent. The bT value is considered the adsorption binding energy, and the AT value can be evaluated as a measure of the adsorption energy, with small AT values indicating physical adsorption (Al-Trawneh et al., 2021).

The Dubinin-Radushkevich (D-R) model is related to the adsorption energy, indicating whether the adsorption is physical or chemical. For EDR values less than 8 kJmol−1, it can be said that physical adsorption occurs. In this study, the EDR value was 13.88, which can be interpreted as chemical adsorption (Kim & Kim, 2019).

After the adsorption process, desorption studies were carried out with 0.1 M HCl, 1 M HCl, 1 M HNO3, and 1 M NaOH for the reusability study of the adsorbent, and the highest recovery of approximately 50% was achieved with 0.1 M HCl. For the reusability study, the samples desorbed with 0.1 M HCl were selected. The samples were subjected to the adsorption and desorption processes three times, and no decrease in the total adsorption amount was observed. However, it was observed that approximately half of the adsorbed mercury was not separated from the adsorbent.

It can be seen that the adsorption capacity is quite high when compared to similar adsorbents listed in Table 2, selected from the literature.

Table 2 Comparison table of various adsorbents
Full size table

5.7 Influence of Time to Adsorption

A series of experiments were carried out to find the change of adsorption over time and the kinetic parameters of adsorption, and the experimental results and the compatibility of these results with the theoretical models such as Pseudo first order (PFO), Pseudo Second order (PSO), intraparticle diffusion (IP) and Elovich (Largitte & Pasquier, 2016) are given in the Fig. 10, and the kinetic parameters found from the models are given in the Table 3.

Fig. 10
figure 10

Effect of time to adsorption and fitting curves of theoretical models

Full size image
Table 3 Kinetic parameters of adsorption and using equations
Full size table

Since the adsorption event takes place in a heterogeneous phase, it is difficult to explain with kinetic models used in homogeneous reactions. Models that are widely used in the evaluation of adsorption kinetics generally provide several parameters such as the adsorption rate constant, accurate estimation of the adsorbed amount in equilibrium, and an opportunity to comment on the change and mechanism of the reaction over time. Although PFO explains the reaction kinetics as a suitable model at the beginning of the adsorption, it is more appropriate with the PSO model to predict the long adsorption time and the amount adsorbed in equilibrium. The experimental data obtained for the change in the adsorption of Hg (II) ions to the Influence of pH of the solution to Hg (II) adsorption onto EWGH@Paa adsorbent over time were found to have high coefficients of fit for various kinetic models. However, the qe values obtained experimentally and the closeness of the qm values from the model to the found one can be considered as a measure to determine which model the adsorption kinetics is suitable for. The results show that the PFO model is suitable for describing adsorption kinetics, but the PSO model can also be used to explain adsorption. The adsorption rate constants are approximate from both models and show very fast adsorption. The half-life found in the PSO model was quite high for the adsorption. The adsorption kinetics can be explained in terms of the parameters obtained from the Elovich model. The Elovich parameters α and β are the initial adsorption rate and desorption constant, respectively (Hosseini-Bandegharaei et al., 2011). The initial velocity is high. These findings show that adsorption is very fast and that the newly synthesized EWGH@Paa adsorbent is useful for Hg (II) ion adsorption. Although the IP model has a low coefficient of fit, the multilinear adsorption curve indicates that intraparticle diffusion also occurs during adsorption.

5.8 Effect of Temperature on Adsorption and Thermodynamic Parameters

To find the thermodynamic parameters of adsorption, the study was carried out at different temperatures, and other adsorption conditions were kept constant, and the results are given in Fig. 11. Adsorption thermodynamic parameters were calculated using the Van’t Hoff equation. The results show that the adsorption is endothermic and the enthalpy is 35.17 kJmol−1. This result shows that the adsorption is in the energy-consuming direction. The adsorption entropy was found to be 183 Jmol−1, i.e. positive. This result indicates that the disorder increases during adsorption. Considering that the free ions in the solution become more regular in the solid phase during the adsorption process, a decrease in entropy is expected, but since this result is the entropy of the whole process, other secondary interactions that occur with adsorption increase the entropy of the system (Abdelmonem et al., 2024). Because together with adsorption, secondary events such as dehydration, ion exchange, and hydrolysis affect the adsorption entropy. Free enthalpy of adsorption was found to be negative for 298 K, as 19.25 kJmol−1. This result is expected because adsorption occurs spontaneously at this temperature.

Fig. 11
figure 11

Effect of temperature on adsorption

Full size image

5.9 Details of Density Functional Theory Calculations

All calculations were performed using the Perdew-Burke-Ernzerhof (GGA-PBE) exchange–correlation functional (Perdew et al., 1996) and 6-31G(d)/LANL2DZ electronic basic set (Francl et al., 1982; Hay & W.R., 1985). The dispersion corrections D3 proposed by Grimme (Grimme et al., 2010) were also included to take into account the weak non-covalent interactions. So, the PBE-D3/6-31G(d)/LANL2DZ level of theory is applied. We used the graphics processor-based TeraChem software (Goumans et al., 2009; Kästner et al., 2009; Titov et al., 2013; Ufimtsev & Martínez, 2009). Geometry optimization was carried out with the efficient geomeTRIC energy minimizer (Wang & Song, 2016). Conceptual Density Functional Theory (CDFT) considered as a branch associated with the chemical reactivity of DFT presents the following mathematical relations to define the chemical potential (µ) and chemical hardness (η) (Islam et al., 2018).

$$\mu = - \chi = \left[ {\frac{\partial E}{{\partial N}}} \right]_{\nu (r)}$$
$$\eta = \left[ {\frac{\partial \mu }{{\partial N}}} \right]_{\nu (r)} = \left[ {\frac{{\partial^{2} E}}{{\partial N^{2} }}} \right]_{\nu (r)}$$
$$\sigma = 1/\eta$$

Here, E, N, and ν(r) are total electronic energy, total number of electrons, and external potential, respectively. As can be seen from the relations presented above electronegativity (χ) corresponds to the negative of the chemical potential while softness (σ) is defined as the multiplicative inverse of the chemical hardness. If one applies the finite difference approach to the aforementioned mathematical relations, ground state ionization energy (I) and electron affinity (A) based hardness and chemical potential equations can be obtained as (Kaya et al., 2023):

$$\mu = - \chi = - \left( {\frac{I + A}{2}} \right)$$
$$\eta = I - A$$

According to Koopmans Theorem (Koopmans, 1934), via frontier orbital energies (HOMO and LUMO energy values), the ionization energy and electron affinities of molecules can be approximately predicted as:

$$I = - E_{HOMO}$$
$$A = - E_{LUMO}$$

In the present work, we used the Koopmans Theorem to predict the ionization energy and electron affinities of the predominantly found molecules in green walnut shell and their Hg (II) complexes.

5.10 Molecular Complexes

First of all, we optimized the structure of the two-molecular complexes containing Hg (II) ions. We considered the ion-containing complexes as the singlets. The electronic and energy characteristics of the considered systems are presented in Table 4. The binding energy was determined as follows:

$$E_{b} = E\left( {{\text{molecule}}} \right) + E\left( {{\text{Hg}}^{2 + } } \right) - E\left( {{\text{molecule/Hg}}^{2 + } } \right)$$

where “molecule” is tannic acid, ellagic acid, sinapic acid, juglanone A, and juglanone B.

Table 4 Calculated electronic and energy characteristics of, ellagic acid, sinapic acid, juglanone A, juglanone B, and their complexes with Hg (II) ion
Full size table

One of the most popular parameters used in the chemical reactivity analysis of the chemical system is the chemical hardness. This concept introduced by R.G. Pearson is defined as the resistance against the polarization of atoms, ions and molecules (Kaya & Kaya, 2015a, 2015b). There is a remarkable relation between quantum chemical parameters like hardness, polarizability and stability. The relations with stability of such parameters are illuminated through some electronic structure rules such as Maximum Hardness Principle (Kaya et al., 2022) and Minimum Polarizability Principle (Kaya et al., 2016). Maximum Hardness Principle (MHP) states that stable chemical states correspond to minimum softness or maximum hardness value. It is clear from this explanation that hard chemical systems are more stable and hardness can be used as a stability indicator. The verbal definition given above for chemical hardness implies the inverse relation between polarizability and chemical hardness concepts. This inverse relation introduced by Ghanty and Ghosh (Ghanty & Ghosh, 1993) has been instrumental in introducing the Principle of Minimum Polarizability (PMM) to science by Chattaraj and Sengupta (Chattaraj & Sengupta, 1996). According to PMM, polarizability is minimized at stable states unlike the chemical hardness. As a measure of the polarizabilities of the studied chemical systems, we calculated their dipole moments and presented in the related table. The emergence of the chemical hardness concept has been realized with the introducing of Hard and Soft Acid–Base (HSAB) Principle (Pearson, 1963). Through HSAB Principle, Lewis acids-base are classified as hard, bonderline and soft. Hard acids prefer the binding to hard bases and soft acids prefer the binding to soft bases because of the power of the interactions between the mentioned species.The most stable sytem among the dominant component of green walnut shell is ellagic acid with a chemical hardness value of 2. 844 eV. The most reactive or soft system is juglanone B with a chemical hardness value of 1.943 eV. It should be noted that in hard and soft classification of Pearson, Hg (II) ion is among widely known soft acids. In the light of HSAB Principle, it is not difficult to predict that this ion will more powerful interact with the most polarizable or soft molecule among the dominanat components. As expected, the binding energy (Eb) calculated for the interaction between Hg (II) and juglanone B is higher than the calculated binding energies for other chemical interactions. This situation shows that our theoretical and experimental observations are in good agreement with HSAB Principle. The mechanism of the interaction between Hg (II) and juglanone B is visually presented in Figs. 12–13. Figures regarding to the interaction with Hg (II) of other components are presented in the Supplementary File of the paper.

Fig. 12
figure 12

Juglanone B: atomic structure (a), HOMO (b), and LUMO (c)

Full size image
Fig. 13
figure 13

Juglanone B/Hg (II) complex: atomic structure (a), HOMO (b), and LUMO (c)

Full size image

6 Conclusion

The high amount of water-soluble part of the green shell, which is released in a very high amount during the walnut production process, poses a serious danger to the environment. The water-soluble component is high in terms of functional groups and consists of active biomolecules. It has been shown that by incorporating this part into an inert polymer structure, it can be an effective adsorbent, especially for metal removal. This feature of the adsorbent has been experimentally shown to be highly effective for mercury removal, with high adsorption capacity and fast adsorption. The aim of this study is to transform a structure that is currently in waste and has a limited application area for use as a usable adsorbent. The results showed that this method is promising for future studies.