Dynamical Modelling of the Global Cement Production and Supply System, Assessing Climate Impacts of Different Future Scenarios

Abstract

The global cement and concrete demand, production, supply, and the general global market price was modelled using the WORLD7 model for different future scenarios. The model was used to analyze some possible measures to reduce the climate impact of cement production. The main result from this study is that three factors may bring regulatory limitations to be imposed on cement production. The contribution of CO₂ to the atmosphere, the amount of iron used in construction and the use of energy in production are the main factors that may cause limitations. Cement accounts for about 8% of the global CO₂ emissions and energy use at present, and this fraction is projected by the simulations to continue to increase. To reduce CO₂ emissions from cement production, ending fossil fuel use for calcination, combined with a change towards using mortar as an alternative for making concrete should be considered. Our conclusion is that the long-term limitation for cement production is the availability of carbon-free energy, and the availability of iron for reinforcement bars. Eliminating the use of hydrocarbons for cement calcination may reduce the future the contribution from cement by 38%. Eliminating the use of hydrocarbons for calcination combined with substituting cement with mortar to 50%, the contribution to the future global average temperature increase is reduced by 62%. Eliminating the use of hydrocarbons for calcination combined with substituting cement with mortar to 90% is a reduction by 90% in the contribution from cement.

1 Introduction

1.1 Background

Cement is one of the world commodities produced in the largest amounts. Figure 1 shows the development of production over time since 1900 to now along with the cement price, inflation adjusted to 1998, was taken from the United States Geological Survey Mineral Summaries Programme, which is publicly available online (USGS, 2022). Cement is from 9 to 11% of the weight in modern concrete, thus an annual volume of 4 billion tons of cement in 2018, imply addition of 30–35 billion tons of stony aggregates (Sand, gravel, crush, stone, and recycled concrete rubble) and 700–800 million tons of steel as reinforcement bars (2015) (Barry et al., 2013). A conventional view is that there is for practical purposes endless resources of what is needed for cement and concrete on the Earth; sand, gravel, stone, and energy to calcinate carbonates. Given that we are in the midst of the Great Acceleration in resource extraction and use (Steffen et al., 2015), this view needs to be critically examined. There is no system dynamics model for global cement production available at the present date (Anand et al., 2006; Nakamura et al., 2007; Neuhoff et al., 2014; Sathaye et al., 2010). Cement production and the correlated energy use has been included in a series of econometric models, but then only as statistical correlations without feedbacks to markets, economy or system dynamics like recycling and effects of price on demand (Akashi et al., 2011).

Fig. 1

a Supply for cement and burned lime (CaO) from 1900 to 2015. b Market price in $ per ton, inflation-adjusted, using 1998 as the reference year. Data from the USGS 2022 mineral commodity summaries

Construction materials, such as sand, gravel, stone aggregates, and rock, are fundamental for human development and wellbeing. The materials play a central role in the global economy, and stony aggregates are one of the largest material flows humans move around in terms of weight. The United States Geological Survey (USGS, 2022) and UNEP GEAS (2014) estimate that sand, gravel, and stone materials used in construction amount to about 47–59 billion tons per year; the range show the uncertainty in the estimate. Sand and gravel account for both the largest share (from 65 to 85%) of that stated above. It is not so that any sand or gravel will do for making good concrete. Specific product qualities are often required, and the available resources for these qualities can be limited. In order to assess the sustainability situation for the global cement production, a proper model for the cement production and use system is required, before any serious advice can be given. The model must be mass balance and energy balance consistent to be a serious model. Econometric formulation or statistical relationships will not do for a model with industrial relevance. The challenge is that such a model is missing at present.

The world’s use of stony aggregates for concrete can be estimated at 26–30 billion tons a year for 2012 (Giljum et al., 2008, OECD, 2018a, 2018b). China, India, Brazil, USA, and Turkey are currently the world’s biggest concrete producers, with China and India accounting for two thirds of total global production. In the past 20 years, cement demand in China has increased fourfold compared to a growth of about 58% in the rest of the world (UNEP, 2011). There are significant concerns about the sustainability of present global material extraction rates, including the issue of sand, gravel, and stone extraction rates (Bardi, 2013, Giljum et al., 2000; Heinberg, 2011, Krausmann et al., 2009, Meadows et al., 1974, 1972, Sverdrup & Ragnarsdottir, 2014, Sverdrup et al., 2017a, 2017b, 2017c).

Figure 1 shows the supply (a) and price (b) for cement and burned lime (CaO) from 1900 to 2015 as recorded by the USGS (2022). Calcite is used for cement production, burnt lime is used in mortar and in many metallurgical processes. In many cases, the cement is the glue of a mix of sand, gravel or stone, and may be as little as 10–15% of the bulk material (Table 1). From 2015 to 2020, the production curve stayed nearly flat. The data was adapted using information from USGS (2015-2021) and Statista (2015-2021). The demand is predicted to increase towards 2025 (Research & Markets 2021). This data is used for validating performance aspects of the model simulations. The largest CO₂ emitters on a global level from human activities are as follows: fossil fuel combustion (oil, gas, coal, peat), iron and steel production (use of coal or gas), cement production (calcinate carbonate rocks), metal production (fossil fuels use and some calcination of carbonate minerals), and production of sand, gravel, and stony aggregates is to a large degree counted into fossil fuels.

Table 1 Typical composition of concrete showing the weight fractions of different materials used in construction (Andrew, 2018)

Making cement implies calcinating carbonates (mostly CaCO₃), releasing the CO₂ to the atmosphere. This is normally done by heating the cement kilns with coal, in a few cases with gas or oil that release CO₂, and in rare cases with electricity. The emissions of CO₂ from the coal used for heating the reaction comes in addition to the CO₂ from the calcination. Cement production is a very significant contributor to global warming (Worrell et al., 2001). It is likely that strong measures to combat climate change will in some way present the cement industry with challenges concerning demands for reduced CO₂ emissions.

1.2 On the Materials

Mortar based on clays and lime go back far in time to before 2000 BC. Mortar is based on calcium oxide, gypsum, and water, and mortar adsorbs CO₂ from the air when it solidifies. The use of mortar today is limited in urban construction but works well with construction based on bricks or stone as the structural main binding element. Lime-based mortar settles slowly but is durable once it is hardened (Despotou et al., 2014). The settling time can be speeded up adding gypsum, but the binding is weaker, especially under wet conditions. However, gypsum plaster is easier to make and requires lower temperatures. The burning of gypsum removes crystal water. Adding silicates like burnt clay minerals or burnt silicate power, allows silica to replace CO₂ in the mortar and concrete is made. It is far stronger and water resistant (Darling, 2011).

Cement with lime, roasted silica, and roasted clay was developed by the Greeks around 500 BC and developed on an industrial scale by the Romans. They used volcanic ash from Pozzoli near Napoli, Italy as the raw material for adding silicate materials. At the end of the Roman empire (476 AD), the knowhow on how to make concrete was lost, and during the Middle Ages, only lime-based mortar was used. Concrete is the composition of cement with reinforcing material of stone and metal. Modern cement and how to make concrete was reinvented in 1824, about 1300 years after the original knowhow from antiquity was lost (Cizer 2009). Concrete and cement have largely replaced mortar in construction during the last 100 years. Cement accounts for about 8% (7–11%), the number varies some between the different sources, see Kermeli et al., (2016a, 2016b) of the global CO₂ emissions and energy use, and this fraction is generally expected to rise (Kermeli et al., 2016a, 2016b; Worrell et al., 2001, 2013; Akashi et al., 2011).

1.3 The Challenge, Objective, and Scope

The purpose of this study was to use an integrated system dynamics assessment model to analyze some possible measures to reduce the climate impact of cement production. A large amount of energy, reinforcement iron and the environmental impact of the derived CO₂ may possibly be a limitation for future cement production. Earlier cement models included in integrated assessment models was flow-sheet-based push-through models, with no feedbacks inside the model. The models included in existing assessment models are often time-series based with simple guesses for future forecasting. At present there is no available assessment model that includes process-based simulation of the cement production and supply system. A model that is mass balance consistent with feedbacks to and from market dynamics is required for future scenarios and serious assessments. The objectives of the study were as follows:

• 1. Develop and create a cement system dynamics model that can be used for sustainability assessment on the global scale. The goal is to make a model that is relatively simple and then continue with details afterwards.

• 2. To dynamically model the global cement demand, production, supply, recycling, and market price dynamics in the global system

• 3. To assess if there are any type of material resource limitations to the global cement production.

• 4. To analyze scenarios for cement production with reduced CO₂ emissions by less use of fossil fuel and using more mortar-based cement that sequesters CO₂.

Cement production is so large that it has an effect on the global energy markets. Fossil fuels will not last forever, and it is a relevant question if there will be enough coal or oil available. It is outside the scope of this study to investigate many alternative demand scenarios, and it is not in the scope to do sensitivity analysis in other aspects than climate change aspects. Adding a cement module to WORLD7 was a long term goal for the authors, linking what goes into making concrete, and as a part of a complete metals and materials part of the WORLD7 model system.

2 Methods and Theory

2.1 General Methods Applied

A number of methods have been combined for this study:

• 1. Model development

  • a. Systems analysis for mapping the global cement system and creating a CEMENT module for WORLD7 leading to causal loop diagrams and flow charts representing the system.

  • b. Integration of the CEMENT module into the WORLD7 structure. Sand, gravel, energy, and iron was sourced inside the existing WORLD7 model.

• 2. Data and parameterization

  • a. Literature and report searches and reading to find necessary data for model parameterization and performance on historical data.

  • b. Earlier assessments by the authors for energy and ferrous metals resources and supply assessment using WORLD7.

• 3. Use the integrated assessment model WORLD7 with the new cement module for running different scenarios

Standard methods of systems analysis and systems dynamics have been used (Senge, 1990; Sverdrup & Svensson, 2004; Sverdrup et al., 2021). Material flow pathways and the causal chains and feedback loops in the cement supply and use system were mapped using a causal loop diagram (CLD) methodology. The resulting coupled differential equations are transferred to computer codes for numerical solutions using the STELLA® systems dynamics software (Fig. 3). For model validation, to assess performance and robustness of the model, the simulations for the past (1900–2015) was compared to the available data for the same period. When the model performance is satisfactory, the model is used to simulate the future (2015–2300) under business-as-usual (BAU) conditions. In this context, it is important to stress that we do not aim to predict or describe the likely future at this future timescale but rather to illustrate implications on resource use and availability under assumed BAU conditions as well as what would happen if something would be changed.

To properly understand the internal feedback system and the dynamics of the WORLD 7 model, to understand its internal couplings and large amounts of feedbacks between many subsystems, it will be necessary to read up on the model. Relevant papers for this are Sverdrup et al., (2013, 2014, 2015, 2021), Sverdrup and Olafsdottir (2018), Olafsdottir and Sverdrup (2019) and Sverdrup and Olafsdottir (2019a, 2019b). Sverdrup and Ragnarsdottir (2014, 2016, 2017) discusses in detail how the reserve and resource assessment were done for the WORLD7 model. For those seeking the details of that, we would send to those publications. In the WORLD7 model, nearly everything is linked in feedback systems, making all responses non-linear.

In order to address the objectives stated, a cement module was developed and included in the WORLD7 integrated assessment model, a module that is able to simulate the production of cement and concrete for the building industry and for infrastructures. From this, the model will estimate demand for sand, gravel, stone, demand for calcination energy and demand for simple steel for reinforcement bars, as well as a secondary effect where construction generates secondary demand for wood, aluminum, copper, zinc, and lead. The present approach differs from earlier approaches by using a fully integrated global materials and economy model.

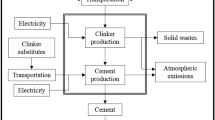
Starting from market data, iterations were used to set the parameterization to such values that the cement supply and cement market price over time could be reasonably well reproduced when compared to available data. The systems analysis and the running of scenarios allows us to see where the intervention points in the system are, and to propose policy interventions (Sverdrup et al., 2019). The model represents a simplified supply chain as has been shown in Fig. 4 (adapted from Elhasia et al., 2013). There, it can be seen that cement production makes a demand in the WORLD7 model for energy, limestone, and sand. The preparation of concrete creates the demand for more sand, gravel, stone, water, and reinforcement bars in iron. The demolition of concrete infrastructures create waste, sand some of that is recycled as stony aggregates to gravel and the reinforcement bars to scrap iron. All of this is handled internally in the WORLD7 model. Based on previous research conducted by the authors it is likely that gravel will not be limiting (Sverdrup et al., 2017a, 2017b, 2017c) for making concrete, if sand and gravel from crush and from recycled aggregate materials are included.

2.2 Model Description

Figure 2 shows the flow chart for the cement system as it is represented in the model. Figure 3 shows the causal loop diagram for the cement module. The causal loop diagram shows the causal relationships in the model, and together with the flowchart in Fig. 1, defines the principles of the system dynamics model (see Senge, 1990 and Sverdrup et al., 2019 for how causal loop diagrams are used and constructed).

Fig. 2

Cement production generates a number of internal system demands in a society. These market demands are covered from other modules in the WORLD7 model

Fig. 3

Causal loop diagram for the cement module in WORLD7 and some of the linkages to energy and iron production. The causal loop diagram shows how the cement demand is modified by energy available, how construction will become restricted by reinforcement bar availability and modified by price. The different R's mark reinforcing feedback loops in the system

It shows how the cement production is linked to the cement market, and how the market is linked to construction and maintenance of a large part of the infrastructure in society. The production is commercially driven by profits, which depend on both income and costs. In the bigger perspective, the cement system (Production, market, construction, maintenance) is linked to the energy market and the iron market. Cement is, because of its sheer production volume, one of the largest single energy users, and through that it has an effect on the market price for energy.

Cement is mixed with fillers (sand and gravel and reinforcement bars) to make concrete. The demand from the concrete market for iron is so large that it has a significant effect on the iron price. The iron price has a feedback to the construction market through the concrete price and the cement production (shown in Fig. 3), whereas the energy price affects the profitability of the cement production. The causal loop diagram shows how the market mechanism operates and how demand and supply are simulated in the model. This is done dynamically, and demand responds to price and availability in every time step. The causal loop diagram shows how the cement demand is modified by energy available, how construction will become restricted by reinforcement bar availability and modified by price. The different R’s mark reinforcing feedback loops in the system.

The loop marked R1 is a reinforcing loop driven by business profits. The loops marked with R2a and R2b are two reinforcing loops driven by construction demand and maintenance demands and infrastructure upkeep. Construction demand is driven by per capita affluence which is correlated with GDP and population, which is derived from the WORLD7 economy module. The cement module is closely linked with the sand, gravel and stone module in WORLD7 through feedback links. To make concrete, sand and gravel and stone ballast is needed in addition to cement. From a fraction of 25% and upward, the energy availability for cement production is gradually restricted, and cement cannot take more than 50% of all energy. For cement, we have one stock for the market (Fig. 2). Sand, gravel, stone, and water is added with the cement and concrete is made into buildings and infrastructures (Fig. 2 and Table 1).

We have one stock for concrete in infrastructures and one for broken down to waste from infrastructures in the model (Fig. 2). This concrete waste is partially recycled to crude sand and gravel. Nothing is recycled back to cement; it reappears as stony aggregate. But a part of the recycled and re-sized sand and gravel will end up in the concrete. The simulations make use of the simple climate change model included in the WORLD7 model. Figure 4 shows an overview of the user interface for the WORLD7 model as it appears in the STELLA Architect system dynamics modelling software. Figure 5 shows the cement submodule in WORLD7. It is beyond the scope of the present study to explain the internal workings of the climate change model in WORLD7, the ferrous metals module (Sverdrup et al., 2018a, 2018b) and the sand, gravel stone supply module (Sverdrup et al., 2017a, 2017b, 2017c), as well as all the other modules now present in the WORLD7 model. The cement module in is closely linked with the sand, gravel, and stone module in the model. This module exchange information with the iron module, the energy module, the population module, and the stony material module in the WORLD7 model structure. The model in Fig. 5 is designed using the flowchart in Fig. 2 and the causal loop diagram in Fig. 3.

Fig. 4

Overview of the WORLD7 model system. The cement module is found in the lower left corner. The cement module communicates with other modules for resources supplied to the production of cement

Fig. 5

The cement submodule in WORLD7 in the STELLA Architect system dynamics modelling environment

2.3 Global Demand for Cement and the Raw Materials Used

The raw materials and natural resources used for cement production are as follows:

• 1. Limestone; this is mostly calcium carbonate in the form of calcite mineral (CaCO₃). This always has some percent dolomite (CaMg(CO₃)₂), and sometimes small amounts of siderite (FeCO₃). Dolomite is sometimes added in the mix. Calcite and dolomite are mined, they are finite resources, but the deposits are truly enormous, most probably inexhaustible. The annual limestone production is about 4.2 billion tons per year (2015). There is a significant regeneration of carbonates by geological processes

• 2. Ironstone is a sedimentary rock composed of iron oxides, carbonate minerals, shale (silicates), and iron carbonate (siderite). Ironstone is mined, it is a finite resource, but the deposits are widespread, but exhaustible. Pure siderite (FeCO₃) is probably an exhaustible resource. When siderite processed to iron, CO₂ is driven off. FeO may be used in cement.

• 3. Gypsum (CaSO₄*2 H₂O). Gypsum is mined, it is a finite resource. The deposits are very large in the size of many hundreds of billion tons. World production is about 260 million tons of gypsum per year (2015). Gypsum can be used in both cement and mortar

• 4. Clay (aluminosilicates, aluminum oxides, aluminum hydroxides). The total deposits are truly enormous, probably inexhaustible for all practical purposes. How large the industrially interesting deposits are, is unknown to us.

• 5. Energy is used in direct proportion to the amount rock calcinated. This was initially applied as coal, later as oil or gas. It is possible to use electricity, as it is about maintaining a high temperature

Cement demand and use is approximately proportional to population times global wealth. Traditionally, cement is made with coal and in special cases, charcoal or oil. In the more distant past, charcoals from wood was used. Other energy sources can be used; oil, natural gas, and electricity (Battaile, 2019; OECD, 2018a, 2018b). Thus, cement production results in a demand for all of these. The cement demand was modelled based on a number of parameters and the numerical values drawn from a number of references (Krausmann et al., 2009; Gutowski et al., 2013; Kermeli et al., 2016a, 2016b; Li et al., 2015; Shan et al., 2019; Bonnet et al., 2019; Xu et al., 2012; Yamaguchi 2018; Zhang et al., 2015). The following parameters were evaluated for setting the world cement demand: Cement demand per person and year follows a pattern with increasing demand during the transition to industrial society with a peak and a decline down to a maintenance level. This is paralleled by the demand development for iron and steel (Taken from Giurco et al., 2013). The cement demand per capita has peaked and declined in most of the industrial countries, China and India are in their major transitional stages now, and Africa is about to start (Bonnet et al., 2019; Kermeli et al., 2016a, 2016b; Li et al., 2015; Shan et al., 2019). A part of the cement demand is taken from the energy module in the WORLD7 structure. Maintenance of stony material-containing infrastructures in use in society creates cement demand. This is based on an annual decay of the infrastructure stock in-use in society. Sand, gravel, stone together with rocks and iron bars for reinforcement gets embedded in cement to make concrete. This is taken together into a general equation that has the following shape as in Eq. 1:

$$\begin{array}{cc}\mathrm{D}=\mathrm{k}*\mathrm{P}*\mathrm{f}\left(\mathrm{A}\right)*\mathrm{g}\left(\mathrm{I}\right)& *\mathrm{g}\left(\mathrm{E}\right)*\mathrm{j}\left(\mathrm{R}\right)\end{array}$$

(1)

In Eq. (1), D is demand, f(A) is a function depending on economic affluency; we are using GDP as a proxy for this. g(I) is an intensity function, specifying how the global demand per year per person goes up with time (Fig. 6), P is the global population in number of persons and k is a scaling coefficient. g(E) is the effect of energy cost on the production cost as discussed earlier. j(R) is the effect of reinforcement by supply limitations, caused by lack of available iron. The numbers to calibrate this relationship came from a number of sources, exemplified by Gutowski et al. (2013), Worrell et al., (2001, 2013) and CemNet (2014) as well as commercial market analysis such as those referred to by NewsChannel-110 (2014). The maintenance demand for material is calculated as:

$${\mathrm{D}}_{\mathrm{M}}={\mathrm{k}}_{\mathrm{M}}*{\mathrm{M}}_{\mathrm{i}}$$

(2)

where k_M is the decay rate of the infrastructure and M_i is the weight of the infrastructure. An inherent assumption is that the decay of the stock-in-use is compensated for by maintenance. When the life time of an infrastructure is passed, it is demolished. The average lifetime is 100 years for sand and gravel in cement used in infrastructures and 200 years for cut stone (Guirco et al., 2013). A building decays with 1–3% at a steady rate which must be replaced by maintenance.

Fig. 6

a The estimated global cement demand per capita and year as a function of time. Units are tons per person per year (adapted from data from several sources on historical consumption combined with future forecasts: Statista 2021, Bonnet et al., 2019, CemNet 2014, Research & Markets, 2021). There are further estimates of cement demand available, with considerable variation for the future. b Applying curve a, results in the demand curve. This is the “low demand scenario.” c The cement demand when modelled as a function of global GDP; this is the “high demand scenario”

Table 1 shows the typical composition of concrete showing the weight fractions of different materials used in construction. When the production of cement is 4.5 billion tons per year, that implies a demand for 1 billion tons of reinforcement iron. It also implies a demand for 11 billion tons of sand and 17 billion tons of gravel and stone. The water demand resulting from making the cement is more than 2.1 billion tons of water (2.1 km³). In addition comes all water used for washing and cleaning at the sites. This amounts to a total of 33 billion tons concrete per year.

Table 2 shows an estimation of available reserves for materials necessary for cement and concrete production. The numbers were derived from earlier studies, this is explained in Sverdrup and Ragnarsdottir (2014), Sverdrup et al., (2018a, 2018b), and Sverdrup (2019). The peak years were read from WORLD7 runs. Durand and Laherrere (2015) give peak years of oil in 2025, gas in 2048 and coal in 2055 based on Hubbert’s model, which are in good correspondence with our dynamic simulation with WORLD7 (Table 2). The annual production of cement is about 5 billion tons per year in 2020, a significant of that is made in China. The most developed nations have gone from a “cement use per person” of almost nothing to about 200–500 kg per person and year during the last 100 years. Nations like Japan and China have played “catch-up” in a shorter time; they have had significantly higher use for some shorter periods. Few other nations have had such a catch-up phase. India has potential for doing something similar and a size that is sufficiently big to matter on a global scale. Raw materials used to produce Portland cement is about 64% calcium carbonate, and the rest is aluminosilicate clay, gypsum, siderite, and sometimes some dolomite and different types of silicates. This is all calcinated in a rotary kiln at 1200–1400 °C, and the burned material, “clinker,” is then grinded to cement powder (Andrew, 2018; Elhasia et al., 2013).

Table 2 Estimation of available reserves for materials necessary for cement and concrete production. Amounts are in million tons. Sand and gravel are limited resources on local and regional scale, but globally, very large resources exist. “High” is high-quality resource; “low” is low-quality sand resource

In the model simulations, cement is made and sold through the market to those that use it. Concrete is made by adding sand, gravel, stone, and reinforcement bars (Table 1) and prepare it with water to pour it into constructions. The original cement powder makes up only 11–13% of the concrete mass. Thus, there is far more concrete around than cement. A large part of the global sand and gravel produced is used to make concrete. Energy is one of the large inputs to cement production. The details behind this simulation and the data used for validation are explained in Sverdrup and Ragnarsdottir (2014). The WORLD7 fossil fuel simulation fits the fossil fuel data for production and market prices simultaneously.

Figure 6 shows the estimated global cement demand per capita as derived from the references cited above. Most developed nations have gone from cement use per person of nothing to about 0.2–0.5 t per person and year during the last 100 years, whereas nations like Japan and China that have played “catch-up” in a shorter time have had significantly higher use for some periods (Statista 2020). From the European curve, it will be suggested that the use per person in China will probably decline during the next 20 years to European levels (0.4 t per capita per year). The demand curve resulting from using the short-term demand estimates, as shown in Fig. 6a, results in a demand curve like that shown in Fig. 6b, when we combine it with the population dynamics. This represents the “low demand scenario.” There is an alternative way to estimate the demand and that is by modelling it using the relationship between cement demand per capita, the global population and global GDP. This gives an equation for the initial demand D₀ as:

$${\mathrm{D}}_{0}=\mathrm{k}*\mathrm{P}*\mathrm{GDP}$$

(3)

This demand is then corrected using feedbacks from iron availability, energy availability, raw material availability and the feedback from price. The dependency of demand on GDP is different for different commodities and involves a lot of uncertainty over time (see GloBULK, 2021 for a discussion). These price to market amount correlations are fairly well documented (Sverdrup & Olafsdottir, 2019a, 2019b) and were used here. Figure 6 c shows the resulting initial demand as calculated this way. This is the “high demand scenario.”

Figure 7 shows the feedback functions that limits the cement demand and feedbacks on energy need and demand for iron. Energy increases the cost as the demand for energy approaches 25% of the global available. Iron limits demand when the reinforcement bar demand approaches 60% of the globally available iron, and on increase in price will decrease demand. Figure 7 c shows the feedback functions that limits the demand in the model. Energy increases the cost as the demand for energy approaches 25% of the global available. Iron limits demand when the reinforcement bar demand approaches 60% of the globally available iron, and on increase in price will decrease demand. In their standard projections, the OECD predict that concrete demand will rise to substantially more than 60 billion tons per year in 2050, and that the cement use will increase from 5 billion tons per year in 2020 to more than 7 billion tons per year in 2050 (OECD, 2018a, 2018b,c). The WORLD7 model simulations are consistent with this, but a little lower. Iron for reinforcement is expected to rise from 1 billion tons per year to about 1.4 billion tons per year (Battaile, 2019). The projected demand increases would require about 4 billion tons of fossil fuels per year under business-as-usual. It is questionable if that amount would be available for iron and cement production alone after 2060 (Sverdrup, 2019, Sverdrup & Ragnararsdottir 2014). It depends very much on what kind of policy there will be concerning the extraction of coal, and how much climate change mitigation will be able to limit coal extraction and use.

Fig. 7

The feedback functions that limit the demand (a). Iron limits demand when the reinforcement bar demand approaches 60% of the globally available iron (b). The response to an increase in price will decrease demand (c)

The OECD demand and production predictions for fossil fuels in particular appears sometimes to have been somewhat redacted for political consumption, and these predictions assume continued economic growth with no end in sight (OECD, 2018a; Battaile, 2019, Research & Markets, 2021). This way of working has effect for demand estimates for large global commodities like cement. Such assumptions appear as not very realistic as compared to current sustainability assessments (Alexandrova & Northcott, 2013; Bardi, 2013; Bookstaber, 2017; Heinberg, 2011). Thus, the OECD predictions must be used only after thorough scrutiny and adjustment (Alexandrova & Northcott, 2013; Beddoe et al., 2009; Bookstaber, 2017; Monbiot, 2015; Sverdrup, 2019; Sverdrup & Ragnarsdottir, 2014).

2.4 Further Feedbacks and Assumptions

The following assumptions made for the cement module inside the WORLD7 model are worth mentioning:

Assumption 1	The cement production is not allowed to take more than 50% of the global energy available, if it is more, we will limit cement production in the model
Assumption 2	When the energy fraction of the total global energy demanded exceeds 10%, then the cost of energy rise sharply, affecting the cost of cement production; Cost = Other cost + energy cost * f(E), were f(E) is the scaling factor for how the increase energy price when the fraction of the global energy demanded by cement goes over 10%. We have set other cost at 40 $/t and energy cost at 20 $/t
Assumption 3	The construction industry cannot demand more that 60% of the global iron available
Assumption 4	When the reinforcement bar demand more than 15% of the globally available, the cost of concrete will go up

Further information on WORLD7 can be found in the references listed at the end. Figure 6 shows the feedback functions that limits the demand in the cement module of the WORLD7 model. Energy increases the cost as the demand for energy approaches 25% of the global available (Fig. 6a). Iron limits demand when the reinforcement bar demand approaches 60% of the globally available iron (Fig. 6b). The response to an increase in price will decrease demand (Fig. 6c).

2.5 Scenarios Applied in the Simulations

Several future scenarios were conducted using the model, based on the following assumptions:

• 1. Scenario BAU: Business as usual, 0.5 t CO₂ per ton cement in 2020 from calcination and 0.2 t CO₂ from heating the reaction, nothing is sequestered back into the concrete on solidification

• 2. Scenario FFP: Fossil fuels free production: 0.5 t CO₂ per ton cement in 2020 from calcination and 0.02 t CO₂ from heating the reaction, nothing is sequestered back into the concrete on solidification

• 3. Scenario FFP-HM: Fossil fuels free production: 0.5 t CO₂ per ton cement in 2020 from calcination and 0.02 t CO₂ from heating the reaction, 0.22 t CO₂ per ton cement is sequestered back into the concrete on solidification

• 4. Scenario FFP-AM: Fossil fuels free production: 0.5 t CO₂ per ton cement in 2020 from calcination and 0.02 t CO₂ from heating the reaction, 0.44 t CO₂ per ton cement is sequestered back into the concrete on solidification

The energy source for heating the process is assumed to start in 2030 and the switch to mortar-based concrete is assumed to take effect from 2040.

3 Results

3.1 Business-as-Usual Simulations

The simulations were made for BAU as well as a number of possible future scenarios. The outputs have been shown in Figs. 8–17. Figure 8 shows some of the simulation outputs from the WORLD7 model. Figure 8 a shows the demand, supply, and production of cement. Demand is the demand based on what the population would ask. Energy modified is the demand after adjusting for how much energy is really available; more demand increases the energy cost and thus the production cost. Iron modified is adjusting the cement demand depending on how large a fraction of all iron that is available globally is demanded. A fraction approaching 50% of the global iron supply after 2140 makes iron reinforcement bars hard to get and demand for concrete goes down (Fig. 7b). After 2020, this limitation kicks in, normally through higher energy price. Price modified is the final demand after adjustment for higher price. When the cement price goes above 100 $ per ton, the demand starts to decline. The biggest reduction is because of energy and this starts when the cement production reaches about 5 billion tons per year. Figure 8 b shows how much cement as concrete goes to construction, maintenance and how much is originating from demolition and how much of that which is recycled as aggregate. In poor societies, the recycling is high because of lack of purchasing power to buy new material, in rich societies, recycling is both a monetary issue and one of culture and regulations.

Fig. 8

Simulation outputs from the WORLD7 version 7.156 model. a The demand, supply, and production of cement in the low future demand scenario. The significance of the different lines is explained in the text. b How much cement as concrete goes to construction, maintenance, and how much is originating from demolition and how much of that which is recycled as aggregate. The peak shape of the curve originates from the demand driven by the population numbers

Figure 9 a shows the cement stocks in infrastructure and the stock of rubble from discharged buildings and buildings under deconstruction. Figure 9 b shows the fraction of the scrap flux that is recycled. simulation outputs from the WORLD7 model for cement and concrete available per person. The stock-in-use per person is the amount providing service to the citizen, and the supply per person and year is the amount available for repair, replacement, and expansion per year.

Fig. 9

Simulation outputs from the WORLD7 model. a The stock of concrete in buildings and infrastructure and as demolition rubble. b The fraction of demolition rubble that will be reused as stony aggregate. It is not recycled to cement, but can be reused in concrete

Figure 10 a shows the supply per person per year (kg per person per year) and the stock of concrete on use per person (kg per person). The simulation shows that the production per capita stagnates after 2030 and the curve remains flat after that, suggesting no further economic growth after that date. The stock-in-use stagnates after 2100 and the development after that depend on the development of the populations curve. Figure 10 b shows the simulated market prices for coal and steel. The recycled amount increase in response to increases in sand market price.

Fig. 10

Simulation outputs from the WORLD7 model. a The supply per person per year (kg per person per year) and the stock of concrete on use per person (kg per person). b The simulated iron price and coal price in $ per ton

Figure 11a shows the simulated global cement spot price and the cost of production. Three curves are shown: the price as dependent on market mechanisms only, and estimate based on production cost plus 15% in supply chain business margin. This is a very low margin, equivalent to assuming a very efficient market. We have assumed that nobody produce cement with deficit for any significant time. In the model we have calculate the market price and a price based on production cost plus a margin. We also calculate the maximum of those two curves. All curves are very close as can be seen in Fig. 11a.

Fig. 11

Tahe simulated cement price and cost of production 1900–2200. b The amount iron demanded for reinforcement bars and iron beams by the use of the concrete production in society as simulated by the model. Compared to cement prices around 2000, there is a slight price increase associated with increased energy costs

Figure 11 b shows the iron demand as fraction of the global total iron demand for all purposes, coming from use of reinforcement bars in concrete as simulated by the model.

Figure 12 a shows the total amount of iron produced and the amount iron demanded for reinforcement bars and iron beams by the use of the concrete production in society as simulated by the model. It is evident from the figure that a significant part of the global iron production goes to constructions made in cement and concrete. The simulations do not indicate that iron will become limiting for construction use of cement and concrete. Figure 12 b shows the outcome of an alternative scenario where we use demand modelled as a function of GDP, including the catch-up of production in China during 2000–2015. The demand is estimated as a cement demand per capita, multiplied with the global population, and with an enhancement factor for 2000–2025 for the Chinese production catchup in built infrastructure. Chinese production reached the saturation point in 2015–2016 for cement use and will slowly decline after 2020 to European levels of cement use per capita. From 2020, India will arrive at a similar, but slower process of infrastructural catch-up. The demand and production is the same as the Business-as-usual standard case until about 2015, after which the supply becomes bigger in the long run in this scenario.

Fig. 12

a The amount iron supplied, the amount iron going to reinforcement bars and that as a fraction of the total. b The outcome of an alternative scenario 2 where we use demand modelled as a function of GDP, including the catch-up of China during 2000–2015. The demand and production is the same for both scenarios until about 2015, after which the supply becomes bigger in the long run in this scenario than in the first scenario

3.2 Validation of the Model Performance on Data

Figure 13 shows the simulation outputs from the WORLD7 model when compared to available data on production and market price. Figure 13 a shows the simulation for cement supply as compared to the observed data according to the USGS (2011). The correlation to the data for production appears to be very good, and we can see that there is no build-up of bias in the model when we plot the cumulative production as observed and simulated over time together (Fig. 13b). The two diagrams verifies that the model do reproduce the observed production from 1920 to 2020 with good accuracy. Figure 13 c shows the price as compared to the observed data (USGS 2011). The price level is captured, but the small short-term variation are only partially reproduced by the model. The level is reproduced and some of the variations in the later part of the period. The period before 1960 shows some discrepancy from the data. There was not a fully functioning global market before 1960, and a significant part of the production was under governmental command-and-control management.

Fig. 13

Validation. Simulation outputs from the WORLD7 model. a The simulation for production as compared to the observed data. b The cumulative production price as compared to the observed data. The simulation appears as reasonable. The data was adapted using information from USGS (2015–2020) and Statista (2015–2021)

3.3 Scenario Analysis

3.3.1 Different Demand Function

Figure 14 shows a comparison of the effect of two different ways of making the demand for the future. The two demand scenarios tried were:

• 1. A scenario using demand based on market analysts and the assumption that global demand has peaked

• 2. A scenario where China does a grand catch-up during 2000–2015 on top of a demand function based on population, a per capita factor and the global population as simulated by the WORLD7 population module.

Fig. 14

Comparison of results using the low future demand scenario, considering the apparent global demand stagnation (a) and the high demand scenario resulting from scaling cement use to GDP development (b). The diagrams below (c, d) shows the stocks in use (kg/person) and the supply (kg per person per year) for the two scenarios. e, f The CO₂ emission and their fraction of the global CO₂ emissions

The high demand leads to situations where the cement production may be somewhat limited by resources, whereas this is not pronounced in the lower demand case. The cement supply intensity seems to get into the lower reaches of what is normally discussed as the cement use (the point is about 0.6–0.8 t per person and year, depending on source) saturation level. The authors think the data support the higher estimate rather than the low, but this shows the potential range in the future. The output from this scenario is shown in Fig. 14. Figure 14 a and b show the demand and supply for both scenarios. Figures 14 c and d show the stocks in use (kg/person) and the supply (kg per person per year) for the two scenarios. Figure 14 e and f show the total global CO₂ emissions, the emissions coming from cement production, and the cement CO₂ emissions as fraction of the total global CO₂ emissions, for the low and the high demand scenarios. The energy use for making cement and concrete is very significant. The industrial transition of China, India, and many other countries improving their economy use huge amounts of cement for doing so. The cement use in China stagnated during 2014–2020 but has since started to increase again. Other parts of the world have increased further, compensating for the decrease in demand growth in China, leading to an overall global increase.

3.3.2 Different Climate Change Impacts from Changing Production and Product

The scenarios were defined earlier and are summarized in Table 3. It shows an overview of the scenarios, the basic assumptions made in them, and the simulated effect on the global temperature increase in °C using the WORLD7 model. Figure 15 shows how the different measures used in the scenarios have been phased in over time. Figure 15 a shows the change from using fossil fuels to heat the cement process to emission-free energy sources, was implemented from 2030 to 2060. In principle, we have assumed the energy used for the process to come mainly from electricity from hydropower. Figure 15 b shows the phasing in of mortar-based concrete in order to sequester back the calcination release of CO₂. It is known that CO₂ sequestration back into mortar-based concrete on solidification, but it can take considerable amounts of time, in some cases, several centuries when the cast walls are very thick (Despotou et al., 2001). This can be considered in the design of the building and in the design of the concrete formulation, but still, the delay is significant (30–200 years). We have assumed a delay in CO₂ sequestration into the concrete of 80 years.

Table 3 Overview of the scenarios, the basic assumptions made in them, and the simulated effect on the global temperature increase in °C using the WORLD7 model

Fig. 15

a The change from using fossil fuels to heat the cement process to emission-free energy sources was implemented from 2030 to 2060. In principle, we have assumed the energy to come mainly from hydropower. b The change from cement to mortar is assumed to start in 2040 and have full effect in 2170

This will cause the effect of going from silica-based cement to mortar-based to be delayed by about 80 years. This delay is in the same order of magnitude as the delay between the harvest and burning of trees for fuel and the time until they have regrown and sequestered the CO₂ back. Figure 15 b shows the change from cement solidifying with silica to mortar solidifying with CO₂ sequestration is assumed to start in 2040 and have full effect by 2170, 130 years later.

The results of running the scenarios summarized in Table 3 are shown in Figs. 16 and 17. The WORLD7 simulation suggest that under BAU, the global temperature increase will be about 3.3 °C in 2200, 1.4 °C above the Paris agreement target of 2 °C (see Fig. 17a). The model suggests that the primary goal of 1.5 °C increase is no longer reachable (Sverdrup, 2019) and that the world may stabilize at a temperature increase of 3.2 °C. Figure 17 b shows the net CO₂ emissions from the different scenarios as given in Table 3 (the lines show 1 = BAU, 2 = EFP, 3 = EFP + HM, 4 = EFP + AM). By switching to fossil free heating of the cement production process and well as introducing 50% or 90% mortar-based cement will lead to very significant reduction of CO₂ emissions caused by the use of cement (Table 3 and Fig. 15).

Fig. 16

a The graphs show the business-as-usual run with the WORLD7 climate change model for the expected temperature increase and atmospheric CO₂ concentrations. b The net CO₂ emissions from the different scenarios in billion tons CO₂ per year. We have assumed that measures are taken in 2030 concerning conversion to fossil free heating of the process and from 2040 for switching to mortar-based concrete. The lines in b are numbered as follows for the different scenarios: 1 = BAU, 2 = EFP, 3 = EFP + HM, 4 = EFP + AM

Fig. 17

Different total global temperature change for the different cement scenarios. A section of the diagram (a) was enlarged to allow for reading out the effect of introduction different measures on the global temperature change (b). The lines are numbered as follows for the different scenarios: 1 = BAU, 2 = EFP, 3 = EFP + HM, 4 = EFP + AM

We have used the climate change module in WORLD7 to estimate the impact of these reductions on the future global temperature change. Figure 17 a shows different temperature global temperature change for the different scenarios. A section of the diagram was enlarged to allow for reading out the effect of introduction different measures on the global temperature change (Fig. 17b). In Figs. 15b and 16a, b, the lines and the scenarios have the same numbering. Their impact on the global warming can be summarized as this:

• 1. BAU: Under business-as-usual, the contribution to the global temperature increase from cement production and use is 0.21 °C in 2200.

• 2. EFP: Using CO₂ emission-free heating of the production process, the impact of cement production and use is reduced to 0.14 °C in 2200.

• 3. EFP + HM: Using CO₂ emission-free heating of the production process and having 50% mortar-based concrete, the impact of cement production and use is reduced to 0.07 °C in 2200.

• 4. EFP + AM: By using zero CO₂ emissions heating of the production process and having 90% mortar-based concrete, the impact of cement production and use is reduced to 0.02 °C in 2200.

Mitigating cement-associated CO₂ emission have a significant effect on future global climate change. However, much more is needed in order to limit the impact. Iron and steel production are larger contributors to global climate change; however, the combustion of fossil fuels dwarf them both.

4 Discussion

4.1 The Shape of the Curves

The emission curves have a behavior consisting of a period of exponential growth, an intermediate piece with the end of exponential growth and stabilization at a stable level. The reason for this is the way demand is driven by population, increasing disposable income, this leads to the typical demand per person and year, The following parameters affected the shape of the curve the most: the population over time development, and with it general consumption is an important determinant for demand. The shape of the demand per person and year curve, and the approach to infrastructural saturation. The shape of this curve was taken from the scientific literature and UNEP reports from the International Resource Panel. In the model a technology development curve is used, this was adapted after results like those presented by Gutowski et al., (2008, 2014) and Dahmus and Gutowski (2007).

4.2 Material Constraints

It can be seen that a few of the key resources used for making cement and concrete may create challenges for the cement production (Table 2). Fossil fuels like coal, gas, and oil will be largely exhausted after 2100 and may not be readily available for cement nor iron production (Sverdrup & Ragnarsdottir, 2014). High-quality sand may run into scarcity by 2100 (Sverdrup et al., 2018a, 2018b). For low-quality sand and aggregate, there will be no limits for supply for the next millenniums. Sand can be made from rocks by grinding and sorting, but this comes at a significantly higher cost. Limestone as calcite and dolomite are abundantly available for the next 10,000 years and do not impose mass balance limitations on cement production. Most important is the effect of price increases as a result of energy price increases and scarcity of available fossil fuels normally used for cement. Iron reinforcement bar scarcity plays a minor role as compared to the fossil fuels effect (Fig. 8). The main effect of iron scarcity will be expressed as increased steel prices (Sverdrup & Olafsdottir, 2019b; Sverdrup & Ragnarsdottir, 2014).

4.3 Environmental Constraints

Cement is a major consumer of fossil fuels at present (8.5% of the total fossil fuel in 2020 in WORLD7) and because of this a major source of CO₂ emissions to the atmosphere. It takes on the average 0.33 t of coal to make 1 t of cement for the calcination, and about 0.2 t coal energy equivalents for running other aspects of the production like grinding, transport, and distribution. This is amplified by the fact that fossil fuels are used to calcinate, to drive off CO₂ from the source mineral (limestone and carbonate minerals), nearly 5% in 2000, 8% in 2020 of the total fossil fuel (Worrel et al., 2001). About 0.5–1 t of CO₂ is released for every 1 t cement produced and used. This is CO₂ not adsorbed back as the cement solidifies, the binding occurs with silicates instead of carbonate. If the global anthropogenic CO₂ emissions need to be reduced by 80% in the next 30 years, cement will have to be a part of the plan. Since cement is a very important material, it will be a major competitor for available CO₂ emission free energy. It would be possible to create cements based on only silicates to avoid CO₂ emissions, but the silicate calcination would require more energy (which could be a limiting resource). An alternative would be to change from silicate to mortar, which has no or little silicate and reabsorbs CO₂ when it solidifies (Cizer 2009; Lechtenböhmer et al. 2016; Manocha and Ponchon 2018; PCA 2012, 2014). An issue is that mortars settle far slower than modern cement and has significantly less strength. An advantage is that minor cracks tend to selfheal with moisture, CO₂ adsorption, and recrystallization.

4.4 Uncertainties and Certainties

The very long time perspective of the model runs as such is a complicating factor. Very long-term demographic, economic, and technological development are obviously hard to foresee on century and global scales. The model was not intended to capture all details, and it seems to work surprisingly well at the global level. While we can securely assume mass balance principles to be valid at all, other factors are less straightforward. The apparent model output should be seen as a representation of an illustrative future under assumed “business-as-usual” conditions rather than a projection of a likely future as such. Nevertheless, seen as a scenario, the results allow a better informed discussion about the magnitudes of future resources, their long-term use and sustainability than the alternative of no attempt at assessment.

4.5 Policy Implications

The main problem with cement production is the very substantial CO₂ emissions. It may be necessary to cap future CO₂ emissions from cement production, to prevent climate change to progress into very high risk territory. This could be implying a change towards mortar (which reabsorb CO₂ when it sets) or turn towards alternative materials like wood or carbon fibres which stores carbon, and that come from biomass that can be made to sequester carbon, as well as making materials. Other ways to substitute reinforcement bars may exist or be developed (Eide & Hisdal, 2012). One proposal for a partial alternative would be to substitute cement for wood. This will only work for certain types of buildings and face some challenges in large metropolitan areas. Using would for construction on a large scale would certainly compete with other uses such as for pulp and paper, for biofuels and require very strong governance and prevention of corruption for such a substitution to promote further deforestation. There is certainly not building wood available to substitute all cement use with a population of 8 billion.

The sheer size of the global cement production is a problem in itself, pointing towards the fact that the human population may be too big. In the overshoot archetype, the work of Ehrlich (Ehrlich & Ehrlich, 1990, 2009; Ehrlich et al., 1992; 1968) on population, and the studies of Meadows et al. (1974) are still very relevant. The fact that the Earth’s population is 8 billion and not 2 billion as 150 years ago plays a major role in the size of the impact. But at present, that is politically incorrect to say and a bit of a taboo for many to discuss. Problem denial is another political system archetype, which is not willingly discussed (Kegan & Laskow-Lahey, 2014). These elements point towards that the present political attitudes and political cultures are so far unable to handle controversial issues on the global scale.

The long-term limitation for cement production is the availability of energy, the limits induced by sustainable CO₂ emissions (Climate change aspect), and the availability of iron for reinforcement bars. Additional environmental CO₂ limitations come from the fact that cement lets out a half a ton of CO₂ for each ton cement produced. The potential limitation for reinforcement bars will limit the demand for concrete. That may work both ways. It will lead to less projects that cannot be done without reinforcement in the construction. For those buildings where reinforcement bars can be replaced with stone and brick, it will lead to heavier constructions and demand more cement.

4.6 So What Is Different with This Study

This study differs from earlier studies in the sense that this is a paradigm shift in how to model cement production. It is a mass balance flowchart approach, but driven by feedbacks and mechanisms, rather than statistical correlations and forward push-through (Kermeli et al., 2016a, 2016b). There has some partial earlier attempt at modelling cement production (Kunche & Mielczarek, 2021), but it never really lifted beyond the conceptual level, and no model was made. Others have used the statistically based Hubberts model for cement production, something it was not really designed for. They can be found on the Internet in unpublished notes. This is the first time cement has been included in an integrated assessment model, with the feedbacks discussed in many studies actually implemented and included.

4.7 Next Step

The next step in these assessments is to link together the big CO₂ emission sources not linked to resource extraction and metal-making: cement production, production of aluminum, chromium, manganese, copper, zinc, lead, and nickel production, using the WORD7 model. These are the next sectors where we need to assess their climate change impacts and investigate how to make them CO₂ emission free.

5 Conclusions

The long-term limitation for cement production is the availability of energy, reinforcement iron, and the availability of iron for reinforcement bars, and the environmental limitation derived from the fact that cement lets out a half a ton of CO₂ for each ton cement produced.

• 1. A significant portion of the global CO₂ emissions come from the production of cement. Eliminating the use of hydrocarbons for calcination may reduce the future global average temperature increase to 0.14 °C, out of a total contribution of 0.22 °C, or a reduction by 38% in the contribution from cement.

• 2. Eliminating the use of hydrocarbons for calcination combined with substituting cement with mortar to 50%, the contribution to the future global average temperature increase is 0.08 °C, or a reduction by 62% in the contribution from cement.

• 3. Eliminating the use of hydrocarbons for calcination combined with substituting cement with mortar to 90%, the contribution to the future global average temperature increase is 0.02 °C, or a reduction by 90% in the contribution from cement.

Achieving points 1 and 2 appears as realistic but demands an electrification of the calcination process in the cement industry. Substituting 50% of the cement with mortar appears as possible, with high strength cement prioritized for those constructions that demand it. The availability limitation found will be that the cost for cement will go up significantly and decrease demand. Substituting 90% of the cement with mortar appears as very challenging. Mortar does not have the strength required for certain types of constructions like high-rises, off-shore installations, and constrictions like bridges. An open questions to explore would be which of these types of constructions are really essential for humanity and which are not. The large global population size and increasing number of consumers striving for higher and higher standard of living are parts of driving demand. On a finite planet, there is no such thing as unlimited resources. When more people need to share a fixed amount, it means that there will be less for each one.