1 Introduction

In multi-aquifer hydrogeologic systems, when compressible aquitards are present or are interbedded within the aquifers, intensive groundwater pumping causes land subsidence, generating multiple adverse effects from extensive damage to infrastructure to a gradual depletion of the storage capacity of the hydrogeological system (Galloway and Burbey 2011; Bagheri et al. 2019). Each of these processes occurs gradually depending on the characteristics of the hydrogeological system; the time scales involved in the system's response to anthropogenic disturbances can be very large and diverse (Rousseau-Gueutin et al. 2013; Currell et al. 2016) and the time for an aquitard to reach equilibrium in the face of a disturbance can take hundreds of years (Rudolph and Frind 1991; Zapata-Norberto 2019; Zapata-Norberto et al. 2018). These diverse time scales must be considered in groundwater management.

Groundwater management models have been widely applied to evaluate measures to counteract the effects of saltwater intrusion, to evaluate social and hydro-environmental policies, and evaluate new sources of water supply (Abd-Elaty et al. 2021; Khatiri et al. 2020; Zhu 2013). Pumping strategies for subsidence control have also been investigated without explicitly incorporating land subsidence variables within the model constraints but focusing on limiting drawdown (Qin et al. 2018; Chang et al. 2007, 2011; Psilovikos 2006; Steinbrügge et al. 2005; Maddock 1972).

Chang et al. (2007) developed an optimal stochastic groundwater management model explicitly considering land subsidence. By neglecting transient effects within the aquitard (assuming that the time required for the aquitard to reach steady state given a perturbation in hydraulic head is smaller than the management time period), they employ an uncoupled representation of groundwater flow and consolidation and the response matrix technique for the deterministic management groundwater model. They consider random hydrogeologic parameters and, by using a first-order variance-estimation method, transfer the original deterministic management model into its stochastic form. Chang et al. (2011) extended the deterministic model to simultaneously consider inelastic and elastic compaction. In these two works the transient effect in the aquitard was neglected, i.e., they assumed that the time required for a perturbation (drawdown) to be transmitted to the full thickness of the aquitard is much less than the time step used in the optimization model. However, this is not applicable in hydrogeological systems that include highly compressible aquitards such as those found in Mexico City, where the aquitard response time can be hundreds of years (Rudolph and Frind 1991; Ortega-Guerrero et al. 1999; Zapata-Norberto et al. 2018; Zapata-Norberto 2019).

Díaz-Nigenda (2022) proposed a methodological approach to identify the transient effect in an aquitard and include it in a groundwater management model for a multi-aquifer system, considering land subsidence induced by pumping; their methodology is based on the theory of Bredehoeft and Pinder (1970) and, in order to apply it to highly compressible aquitards, the propagation of the drawdown through the aquitard is computed using Duhamel's theorem. The model integrated three modules that analyze the optimization of the system, the transient propagation of drawdown through the aquitard and the calculation of land subsidence.

Here, the shortcomings of a partial vision in groundwater management are analyzed through an approach that only considers maximizing pumping and restricting drawdown in the aquifer. This approach may lead to recovery of piezometric levels (drawdown is reduced) in some areas, while increasing drawdown in other areas, causing that a greater area may be affected by subsidence.

On the other hand, the importance of considering the response time of the system is also analyzed. In multi-aquifer systems, aquifer units have a characteristic response time which typically can be orders of magnitude smaller than the characteristic response time of aquitard units, and the magnitude of the latter controls land subsidence. In addition, the importance of timely action when dealing with land subsidence and other adverse effects of groundwater overexploitation is emphasized; early detection of adverse effects is important as well as implementing management measures to mitigate the problem.

2 Materials and Methods

Since hydraulic diffusivity of aquitards is typically several orders of magnitude smaller than that of aquifers, for simplicity we assume that drawdown in the aquifer can be uncoupled from the drawdown in the aquitard during a time step (Neuman et al. 1982).

2.1 Methodology for Land Subsidence Analysis

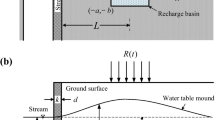
Following Díaz-Nigenda (2022), we employ the response matrix method to compute drawdown in the aquifer at Nc selected control points, due to pumping at Nwell wells. We build a model using Modflow (Harbaugh 2005) and its graphic interface ModelMuse (Winston 2019) to represent a hydrogeologic system composed of an aquifer of thickness b, overlain by an aquitard of thickness b’. From the Modflow model we compute response coefficients \({\alpha }_{m,j,k}\) [L−2 T], which represent the drawdown at the mth control point due to a unit pumping rate at the jth well during the kth time step.

The drawdown within the aquifer, \({s}_{\left(m\right)}\) at the mth control point (observation well) and at the kth time step is computed by

$${s}_{m}\left({t}_{k}\right)={s}_{m,k}=\sum\limits_{j=1}^{{N}_{well}}\left({\alpha }_{m,j,k}{Q}_{j,1}+\omega \sum\limits_{p=1}^{k-1}{\alpha }_{m,j,k-p}\Delta {Q}_{j,p+1}\right)$$
$$\omega =\left\{\begin{array}{cc}0& k=1\\ & \\ 1& k>1\end{array}\right.$$
(1)

where, \({s}_{\left(m,k\right)}\) is the drawdown at the mth control point, [L]; \({Q}_{\left(j,k\right)}\) is the pumping rate of the jth well [L3 T−1] and \(\Delta {Q}_{j,p+1}\) is the change in the pumping rate of the jth well observed in the pth time step, that is,\(\Delta {Q}_{j,p+1}={Q}_{j,p+1}-{Q}_{j,p}\).

To compute the propagation of drawdown through the aquitard, Díaz-Nigenda (2022) employ Duhamel's Theorem:

$${s}_{m}^{\prime}\left(z,{t}_{k}\right)={\int }_{0}^{{t}_{k}}{s}_{u}^{\prime}\left(z,\tau \right)\frac{\partial }{\partial t}{s}_{m}\left({t}_{k}-\tau \right)d\tau$$
(2)

where \({s}_{m}^{\prime}\left(z,{t}_{k}\right)\), is the drawdown in the aquitard at control point m and at elevation z. Equation (2) allows extending the methodology proposed by Chang et al. (2007) to highly compressible aquitards, where storage effects are important. \({s}_{m}^{\prime}\) is the drawdown in a one-dimensional aquitard (in the vertical direction) due to an instantaneous unit drawdown, \({s}_{0}=1\), at the interface with the aquifer, while the other end remains at a constant head, given by the analytic solution (Hanshaw and Bredehoeft 1968)

$${s^{\prime}}_{u}\left(z,{\tau }_{j}\right)={s}_{0}{\sum }_{n=0}^{\infty }\left\{erf\left[\frac{\left(2n+1\right)+\frac{z}{{b}^{\prime}}}{\sqrt{4{t}^{*}}}\right]-erf\left[\frac{\left(2n+1\right)-\frac{z}{{b}^{\prime}}}{\sqrt{4{t}^{*}}}\right]\right\}$$
(3)
$${t}^{*}=\frac{K^{\prime} {\tau }_{j}}{{{S}^{\prime}}_{s}{{b}^{\prime}}^{ 2}}$$
(4)

where, \({b}^{\prime}\) is the aquitard thickness; \({K}^{\prime}\) is the hydraulic conductivity of the aquitard; and \({Ss}^{\prime}\) is the specific storage of the aquitard; \({t}^{*}\) is dimensionless time (Bredehoeft and Pinder 1970). Equation (2) is discretized as

$${{s}^{\prime}}_{m}\left(z,{t}_{k}\right)={\sum }_{j=1}^{N+1}\frac{{s}_{m}\left({t}_{k}+\Delta t-{\tau }_{j}\right)-{s}_{m}\left({t}_{k}-{\tau }_{j}\right)}{\Delta t}{{s}^{\prime}}_{u}\left(z,{\tau }_{j}\right)\Delta \tau$$
(5)
$$N=\frac{{t}_{k}}{\Delta \tau }$$
(6)

Based on (3), Bredehoeft and Pinder (1970) propose that for \({t}^{*}<0.2\) the system is in a transient state, while for larger values of \({t}^{*}\) the flow within the aquitard reaches a steady state and storage effects can be neglected. Díaz-Nigenda (2022) suggested that transient and storage effects are significant even for values of \({t}^{*}\) close to 0.4 and that only for \({t}^{*}\ge 0.5\) flow in the aquitard reaches steady state. Therefore, for \({t}^{*}<0.5\) transient and storage effects need to be considered through our methodology.

The thickness of the aquitard b’ is divided into Nb’ segments of constant length \({\Delta b}^{\prime}\); then total settlement at control point m and time \({t}_{k}\), \({\delta }_{m}\left({t}_{k}\right)\) is computed by

$${\delta }_{m}\left({t}_{k}\right)={{S}^{\prime}}_{se} \Delta {b}^{\prime} {\sum }_{p=1}^{{N}_{{b}^{\prime}}}{{s}^{\prime}}_{m}\left({z}_{p},{t}_{k}\right)$$
(7)
$${{S}^{\prime}}_{s}\approx {{S}^{\prime}}_{se}=\frac{{\rho }_{w}g}{\gamma +2G}$$
(8)

where, \({z}_{p}\) is the elevation of the centroid of the pth segment; \({\rho }_{w}\) is density of water, g is the acceleration of gravity, and \(G \mathrm{and} \lambda\) are Lame constants. For simplicity we only consider irreversible consolidation, that is, if drawdown is positive \({\delta }_{m}\left({t}_{k}\right)\) is computed by (7), otherwise it is zero.

2.2 Numerical Example

A numerical experiment was designed considering a hypothetical multi-aquifer system (Fig. 1) composed by an aquitard that overlies a leaky aquifer. Left and right boundaries are set to constant head (Dirichlet) while upper and bottom boundaries are set to no flow. The aquifer has three zones, each one homogeneous and isotropic but with different hydraulic conductivity, K, and specific storage, Ss (Table 1); three extraction wells (A, B, C) and 8 observation wells/control points (a, b, c, d, e, f, g and h) were considered.

Fig. 1
figure 1

Hypothetical multi-aquifer system

Full size image
Table 1 Hydrogeological and mechanical parameters of the aquifer and the aquitard
Full size table

2.3 Definition of Scenarios

We consider a hypothetical scenario of an aquifer being developed. Pumping rates start from zero and are increased rapidly during the first 5 years to reach 85% of a total annual volume and then keep raising until year 25; this scenario is similar to what has occurred in some regions in Mexico. Pumping rates are then kept constant (which implies a constant annual volume) during another 25 years, for a total simulation time of 50 years. With this as the base scenario, we define two alternatives:

  1. (a)

    Controlling drawdown. A maximum allowed drawdown \({s}_{max}\) is defined, which is enforced at all control points; thus, pumping rates are reduced to ensure compliance in some wells but in others the pumping rates are increased. This strategy is applied from year 26 onwards. Pumping rates that maximize the pumped volume in the system Z subject to drawdown restrictions are computed by solving

    $$Z=max\left\{{\sum }_{j=1}^{{N}_{well}}{\sum }_{k=1}^{{N}_{y}}{Q}_{\left(j,k\right)}\Delta t\right\}$$
    (9)
    $$\mathrm{subject\;to}\;{s}_{m}\left({t}_{k}\right)\le {s}_{max}\quad m=1,\dots ,{N}_{c}$$

    where \({N}_{y}\) is the number of years.

  2. (b)

    Intervention time. Pumping rates are reduced or increased by the same procedure, but this reduction or increase is enforced at earlier times. Different intervention times are employed to illustrate that early action is needed to deal with the “memory” effect of land subsidence.

Table 2 shows some of the characteristics of the analysis scenarios. Figure 2 shows the pumping rates considered in the study cases.

Table 2 Annual pumping rates and drawdown of the test cases
Full size table
Fig. 2
figure 2

Comparison of pumping rates at well A, and aquitard drawdown and land subsidence with the implementation of the base and control drawdown scenarios at control point PC-a

Full size image

3 Results and Discussion

The hydrogeologic system in Fig. 1 has two relevant and contrasting time scales. The first one corresponds to the time required for a perturbation in the piezometric level due to pumping in each well to reach the nearest lateral Dirichlet boundary. Once simulation time is larger than this time scale, drawdown and hydraulic head in the aquifer tend to stabilize. We can approximate this time scale by \({t}^{c}=\frac{{L}^{2}{S}_{s}}{K}\) (Currell et al. 2016), where L is the distance from the pumping well to the nearest Dirichlet boundary. In our example, tc ranges from 0.5 to 3 days for the three pumping wells. The second relevant time scale corresponds to the time for a step perturbation in hydraulic head / drawdown to completely propagate through the aquitard and reach steady state. In this case \({t}^{c}=\frac{{b^{\prime}}^{2}{S^{\prime}}_{se}}{K^{\prime}}\), which leads to tc = 101.5 years; however, based on the analytic solution given by (3), one can assume that the aquitard is close to steady state for half of that time period, that is, \({t}^{*}=0.5\), which leads to 50.75 years, hence the 50-year planning horizon adopted in the test cases.

3.1 Base Scenario

Figure 2A depicts drawdown in control point PC-a, as well as the pumping rate in the nearest well, A. Drawdown rates in PC-a increase as the pumping rate keeps increasing during the first 6 years; the effect of Dirichlet / constant head boundaries is evident as drawdown within the aquifer adjusts quickly to changes in pumping rate and stabilizes (rate of change of drawdown is zero) after year 26. Most of the drawdown within the aquifer (83%) occurs in the first 5 years and after 10 years 95% of the final drawdown has been registered. Figure 2B depicts drawdown propagation within the aquitard at the same location, showing that hydraulic head within the aquitard keeps adjusting with large variation withing the first 20 years. As shown in Fig. 2C, maximum drawdown rates in the first 6 years lead also to maximum subsidence rates (close to 59 cm/year during year 5); total land subsidence is about 5.3 m and more than 50% of this deformation occurs after year 9, continuing during the entire simulation period (rate of subsidence is 0.6 cm/year during year 50), even though drawdown within the aquifer is small after 10 years.

Similar behavior occurs at PC-b (Fig. 3A–C) and PC-c (not shown) in response to pumping wells B and C, respectively. However, in these two areas total drawdown in the aquifer is smaller than in PC-a and therefore subsidence rates and total subsidence are smaller; total settlement at PC-b is 1.8 m (Fig. 3B) and the maximum subsidence rate is 20 cm/year at year 5 (Fig. 3C).

Fig. 3
figure 3

Comparison of pumping rates at well B, and aquitard drawdown and land subsidence with the implementation of the base and control drawdown scenarios in control point PC-b

Full size image

3.2 Controlling Drawdown

This scenario is integrated with pumping rates that maximize the pumped volume in the system starting from year 26, while limiting drawdown in the aquifer to less than or equal to 10 m at the control points. Within this scenario, annual pumping rate is reduced at well A and is increased at wells B and C (Table 2).

3.2.1 Pumping Rate Reduction at Well A

This case illustrates the option of controlling land subsidence by reducing pumping rate. Figure 2D shows that reducing the pumping rate at year 26 leads to recovering piezometric levels in that area of the system (from 13.31 m to 10.405 m, Table 2). Although piezometric level in the aquifer recovers quickly at year 26 (Fig. 2D), recovery within the aquitard takes more time (Fig. 2E) and relatively large subsidence rates are maintained at least 6 more years after drawdown within the aquifer has stabilized (Fig. 2F). This extra time needs to be considered in planning and management. This case leads to a total settlement at year 50 of 4.8 m (Fig. 2F), 0.5 m less than the base case (5.3 m, Fig. 2C).

3.3 Intervention Time

In this section we analyze the case where the pumping rate is reduced at well A at an early time with the aim of controlling or reducing land subsidence at control point PC-a. Figure 4A depicts the evolution of cumulative settlement while Fig. 4B shows annual rate of subsidence, for four cases: the base scenario, when pumping rate is reduced at year 26 to control drawdown to 10 m, and when this reduction in pumping rate is implemented at years 10 and 6. Although maximum subsidence rates are of a similar order of magnitude (between 58 and 64 cm/year) for all four cases and occur between years 5 and 6 (Fig. 4B), total settlement at the end of the simulation period is 5.3, 4.8, 4.1 and 4.0 m for each case, respectively (Fig. 4A). Evidently, reducing the pumping rate is more effective at diminishing total settlement if implemented early, ideally as soon as the negative impact is observed. This might be of the utmost importance in cases of coastal aquifers or near large rivers, as the risk of flooding would increase due to land subsidence.

Fig. 4
figure 4

Comparison of total settlement in the aquitard (point PC-a) with different implementation times of optimal pumping as a measure to control land subsidence

Full size image

4 Discussion and Conclusions

Management strategies to control land subsidence are often seen as stabilizing piezometric levels and, in intensively pumped or overexploited hydrogeologic systems, reducing the disparity in the subsurface water balance. The results obtained here highlight part of the complexity of controlling land subsidence, and the importance of considering the characteristic time scales of the process. It is shown that, in highly compressible aquitards, the characteristic time scale that controls land subsidence can be more than one order of magnitude larger than the characteristic response time of the aquifer. Selection of the management time horizon should consider both time scales. Economic evaluation of the negative effects of land subsidence must consider the fact that ground deformation will continue long after piezometric levels in the aquifer have been stabilized (by implementing managed artificial recharge, for example). Employing the methodology developed by Díaz-Nigenda (2022), which computes the delayed response of an aquitard to pumping in an aquifer by means of Duhamel’s theorem, allows accounting for the disparity in the characteristic response times of the aquifer and the aquitard in a computationally efficient manner. Our work expands the applicability of computationally efficient modeling schemes such as Chang et al. (2007, 2011) to cases when highly compressible aquitards are present in multi-aquifer hydrogeologic systems.

It is also shown that identifying the problem and acting early is important and leads to a significant reduction in the observed total land settlement. In this context, an effective monitoring system registering ground deformation (by topographic surveys or remote sensing techniques such as InSAR) and piezometric levels in the aquifer and the aquitards, is desirable.

Implementing optimal pumping in a multi-aquifer system to control land subsidence needs to consider the restriction of subsidence rates and total settlement, and economic costs of damage to infrastructure, in addition to other restrictions to diminish negative impacts due to intensive groundwater pumping. Of course, all actions should consider all groundwater stakeholders to avoid social, economic, and environmental conflicts.