1 Introduction

Clean drinking water is a basic human need; thus, WDNs (Water distribution networks) are essential infrastructures of every modern settlement. From the smallest villages to the largest cities, properly operating such systems is crucial for the population’s health, quality of life and industrial efficiency. In the last decades, researchers and engineers published papers trying to quantify the resilience (Liu and Kang 2022; Diao et al. 2016), reliability (Walski 1993), or vulnerability (Tornyeviadzi et al. 2021) of drinking water networks. Although there is a significant progression from the original Todini’s resilience index (Todini 2000), numerous papers have developed novel methods (Diao et al. 2016; Zhan et al. 2020; Tsitsifli and Kanakoudis 2010), yet there are still open questions in the field. The main goal is to create quantities that can characterise the behaviour of networks from a selected point of view, thus supporting decision-making in new network design or the analysis of the state of existing networks. This paper follows the path from previous research (Wéber et al. 2020b, 2021) regarding the vulnerability and extends it with the criticality of the isolation valves.

This paper aims to analyse the importance of isolation valve operations during a random pipe burst concerning the consumers in the network. Utility companies are generally responsible for proper functioning WDNs with a strict yearly budget. Moreover, building accurate and calibrated hydraulic models is expensive, or the models are too large for comprehensive analysis. Recently complex network theory tools have been applied to discover the exposed elements in extensive networks (Simone et al. 2022; Giustolisi et al. 2022). The advantages of such quantities are the computational efficiency and the lack of need for a hydraulic model. The questions for this research are the following.

  • How can the utilities prioritise the isolation valves during failures? Are there more crucial valves than others, or are they equally important?

  • If a hydraulic model is unavailable, can any complex network theory quantity be used to estimate the criticality of isolation valves?

The study analyses 14 real-life WDNs from Hungary to answer the above questions. All the models are built for an average demand state, i.e. these are snapshot simulations.

This paper is organised as follows. The next chapter introduces the vulnerability analysis of WDNs and highlights previous results. The mathematical definition of the criticality of isolation valves is introduced in the third chapter, and the results are presented. The fourth chapter represents the approximations of complex network theory tools, while the last chapter contains the conclusions of the work.

2 Vulnerability Analysis

Predicting the vulnerability of water distribution systems in the planning stage and during operation is still a significant challenge. Even with a detailed hydraulic model and a geographic information system database, it is difficult to accurately predict the consequences of a single pipe burst. There are numerous definitions of vulnerability as a quantity in the literature; some of them are based on a topological approach (Maiolo et al. 2018), while some use hydraulics (Wéber et al. 2020b), or both (Tornyeviadzi et al. 2021). This paper considers the interpretation that the purpose of vulnerability is to monitor the general hydraulic behaviour of water drinking networks during a single random pipe burst. If there is a pipe burst, the water company must isolate the affected area to ensure the operation of the rest of the system. At the same time, professionals can carry out repairs and avoid unnecessary water waste or collateral damage. A segment is, by definition, the smallest set of pipelines (and some other hydraulic elements) that can be disconnected from the network by locking the corresponding isolation valves (Walski 1993; Alvisi et al. 2011).

According to (Wéber et al. 2020b), the definition of the local vulnerability of a segment is the product of the failure rate and the relative consumption loss caused by the closing of the segment. Mathematically

$$\begin{aligned} \gamma _i = \alpha _i \beta _i \end{aligned}$$
(1)

where \(\alpha _i\) is the failure rate, \(\beta _i\) the relative consumption loss, \(\gamma _i\) the local vulnerability, and i goes from 1 to the number of segments. The failure rate quantifies the probability of an accidental pipe failure in the segment, where different properties should be considered, such as pipe lengths, material or age (Wéber et al. 2021). Since an accidental pipe failure is inevitable, the failure rate informs only the location of the failure, i.e. it is a normalised quantity, and its sum equals one. The relative shortfall \(\beta _i\) can be estimated using a proper hydraulic model that can cope with pressure-dependent demands and incidentally closed segments, i.e. demand-driven simulations are necessary. Instead of the traditional EPANET (Rossman 2000), an in-house solver STACI (Wéber et al. 2020a) is utilised (similarly to the previous studies (Wéber et al. 2020b, 2021)). STACI is a modular hydraulic solver with a general nonlinear, algebraic solver using Eigen (Guennebaud et al. 2010), validated to EPANET. Since both variables (\(\alpha _i\) and \(\beta _i\)) are between zero and one, so is the local vulnerability. Moreover, the local vulnerability is a segment-specific, dimensionless quantity whose distribution follows a power-law trend (Wéber et al. 2020b). Some segments have primary importance in serving drinking water, while the rest of the network is negligible in vulnerability. Similar results have been achieved recently in the literature (Berardi et al. 2022) with a different real-life network. While these conclusions are based on hydraulics, hierarchical topological metrics also show a power-law trend in vulnerability (Abdel-Mottaleb and Zhang 2021).

The mean relative shortfall can be calculated as the weighted average of relative consumption losses with the failure rates being the weights, i.e. it represents the whole network during an unexpected pipe failure with a single variable, similarly to (Creaco et al. 2012).

$$\begin{aligned} \Gamma = \dfrac{\sum _i \alpha _i \beta _i}{\sum _i \alpha _i} = \sum \gamma _i \end{aligned}$$
(2)

The failure rate is a normalised value, i.e. the denominator is one. It simplifies to the sum of local vulnerabilities. Mathematically the relative shortfall is also a scalar, dimensionless variable for a whole network.

3 Criticality of Isolation Valves

3.1 Overview

Placing the isolation valves in water distribution networks is critical as it greatly affects system shortfall. The N rule (where a node with N connecting pipes has N isolation valves towards each pipe) represents an ideal layout from a hydraulic perspective; however, it is too redundant and not cost-efficient (Walski et al. 2006). Even the N-1 rule is practically too robust and expensive. Many researchers and engineers publish papers about how different layouts affect the segment properties (Liu et al. 2017), the resilience (Liu and Kang 2022), or the shortfall (Atashi et al. 2020). Since the correct valve layout is a complex optimisation problem between the robustness and the cost, multi-objective evolutionary techniques are popular (Yang et al. 2022; Creaco et al. 2010; Lee and Jung 2021). Nowadays, multiple different packages and toolboxes are available for such purposes.

Besides the design of new networks, analysing the operation of existing systems is also beneficial in terms of maintenance. The importance of isolation valves is investigated with topological quantities: betweenness centrality (Giustolisi et al. 2022) and relevance-based betweenness (Simone et al. 2022). Topological metrics have the advantage in computational time; however, they might not be able to catch the essence of some crucial scenarios due to neglecting the hydraulics (Creaco et al. 2012). This paper presents the definition of the criticality of a single isolation valve based on hydraulic modelling during the segmentation of an accidental pipe break.

3.2 Definition

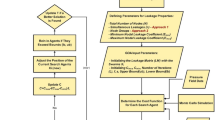
If proper operation (and existence) of every isolation valve is assumed, the average shortfall \(\Gamma _{orig}\) due to a random, single pipe failure can be calculated with hydraulic simulations. However, a valve malfunction (or non-existence) can increase the relative average shortfall as a larger segment might need segregation, see Fig. 1. Note that the figure is a simple example for demonstration. The average shortfall in the case of the ith valve \(\Gamma _i\) malfunction can also be determined with hydraulic simulations. By definition, the increment in the average shortfall is the criticality \(C_i\), i.e.,

$$\begin{aligned} C_i = \Gamma _i - \Gamma _{orig}. \end{aligned}$$
(3)
Fig. 1
figure 1

Demonstration of the malfunction (i.e. missing or not operating) of an isolation valve in a simple WDN. In this example, isolation valve B cannot be closed; thus, S1 and S2 segments must be segregated if there is a pipe failure in either of those segments

Full size image

An isolation valve with \(C_i\) criticality is considered essential if the increment of the relative average shortfall is significant, i.e. \(C_i\) is high. The shortfall can increase with the demand of the additionally closed areas directly, to the unintentionally closed areas, or due to hydraulic reasons. A site might be topologically connected; however, the network still cannot serve enough pressure for all the consumers. Since the relative average shortfall is dimensionless, so is the criticality.

Calculating the shortfall \(\Gamma\) requires \(N_{seg}\) number of hydraulic simulations (one simulation for each segment closure), and the criticality needs \(N_{iso}\) number of shortfall simulations. \(N_{seg}\) represents the number of segments, and \(N_{iso}\) the number of isolation valves. Both numbers can exceed thousands or even ten-thousands for a real-life network. The criticality analysis requires \(N_{seg}*N_{iso}\) number of simulations, i.e. a total evaluation is computationally expensive.

3.3 Results and Discussion

Fig. 2
figure 2

Steps to create the special probability density function (PDF) with logarithmic scaling from raw data for Network 2. a Original data, b Probability density function (PDF), c PDF with dots, d PDF with a logarithmic scale

Full size image

Since the criticality values cover several orders of magnitudes for real-life networks, a special probability density function (PDF) is applied for the proper visualisation. Figure 2 demonstrates the steps to create the PDF for Network 2. Inset a) includes the original raw data for each valve. Indicating the criticality value of each valve (e.g. in (Liu et al. 2017; Simone et al. 2022)) is hard to follow and challenging to identify the actual distribution of the metric, especially in the case of multiple networks or large systems with thousands of valves. Moreover, it cannot illustrate the mathematical distribution of the values. A classic PDF is drawn with columns at Inset b). The PDF is similar to a histogram, but the y-axis does not represent the frequency but the probability density of finding a value at that x location (Montgomery and Runger 2003). Although Network 2 contains only 25 isolation valves, the columns can be barely seen due to the extensive range between the lower and higher values. A logarithmic scale is necessary for presenting the criticality of large networks. Since drawing columns is difficult with logarithmic axes, only the centre point of the column is marked, see Inset c). Finally, the logarithmic scaling is applied for both axes. The same procedure is followed for every network.

Fig. 3
figure 3

The probability density function (PDF) of the criticality of isolation valves in 14 real-life WDNs indicates a power-law trend. Each point visualises several isolation valves. Practically, the proper operation of some valves (on the right of the figure) is crucial, while the criticality of the rest is negligible

Full size image

Figure 3 contains all the results from 14 real-life WDNs. As both axes use a logarithmic scale for proper visualisation and all the points are located along a linear, the distribution is power-law. Similar property of the segments is presented in (Wéber et al. 2020b). Practically it means that the operation of some isolation valves is essential in terms of water service, while the rest of the valves can be neglected. Moreover, water utility companies can distribute the financial sources accordingly, i.e. the valves with high criticality can be prioritised during maintenance, ensuring their proper operation. For example, in Network 2, the raw data is presented in Fig. 2 at Inset a). Some outstanding values have significantly higher importance, while most valves have around zero criticality. Similar phenomena were found by Giustolisi et al. 2022 with topological quantities; however, without the proper visual representation, which is the PDF, the exact distribution could not have been found.

4 Network Theory Estimate of the Criticality

4.1 Overview

The complete criticality analysis of a WDN requires \(N_{seg}*N_{iso}\) number of hydraulic simulations that practically means millions. Even with a computationally effective solver and high-performance computers, the amount of CPU time might be unfeasible. Moreover, the size of the networks tends to grow continuously. Recent years brought numerous handful tools from complex network theory which require negligible computational time while still being able to cope with the essence of the network in terms of its reliability (Giustolisi 2020) or vulnerability (Diao et al. 2014). The goal is to find a strong correlation between a hydraulic metric and a topological quantity that can be used for an estimate (Meng et al. 2018; Giustolisi et al. 2019). The main idea of our proposed technique is similar to the on in (Abdel-Mottaleb and Walski 2021), but instead of the shortfall, a correlation is searched between the criticality and a topological quantities.

Since the nature of the criticality follows a power-law trend, Spearman’s rank correlation is applied, quantifying the monotony between the two variables. Spearman’s rank correlation equals one if one quantity increases, and so does the other for every variable pair, even if not linearly. It is equal to minus one if one grows and the other decreases. In general, Spearman’s rank correlation is between minus one and one, and the closer the coefficient is to one (or minus one), the stronger the relationship is. It can be calculated as the correlation coefficient, or Pearson correlation coefficient, between the rank variables. (Myers and Well 2003).

4.2 Topological Quantities

This section presents the examined topological metrics briefly. For detailed information about the metrics, see the cited papers. Each quantity is calculated using the NetworkX (Hagberg et al. 2008) package in Python 3.6.9. Some metrics are defined for vertices, while the focus is on the edges. In such cases, the graph is transformed into a line graph, with a node for each edge and an edge joining those nodes if the two edges share a common node (Hemminger and Beineke 1978). In other words, it transforms the nodes into edges and the edges into nodes. Every metric is calculated for the segment graph of the networks, where segments are the nodes and the connection edges are the isolation valves (Wéber et al. 2020b; Simone et al. 2022). Table 1 summarises the data of the quantities: name, notation, reference, and whether link graph transformation is needed.

The betweenness centrality \(T_{B}\) of node v is the sum of the fraction of all-pairs shortest paths that pass through

$$\begin{aligned} T_{B}(\nu ) = \sum _{s,t\in V} \dfrac{\sigma (s,t\mid v)}{\sigma (s,t)} \end{aligned}$$
(4)

where V is a set of nodes, \(\sigma (s,t)\) is the number of shortest paths between node s and t, and \(\sigma (s,t\mid v)\) is the number of those paths passing through node v (Giustolisi et al. 2019). A node has a high betweenness value if there is numerous shortest path passing through, i.e. it is located at the centre of the graph. Line graph transformation is necessary for this metric.

The edge betweenness centrality \(T_{EB}\) is directly defined for edges, i.e. there is no need for line graph transformation.

$$\begin{aligned} T_{EB}(e) = \sum _{s,t\in V} \dfrac{\sigma (s,t\mid e)}{\sigma (s,t)} \end{aligned}$$
(5)

where e indicates an edge of the graph, and the other notations are the same.

The closeness centrality \(T_{C}\) of node u is the reciprocal of the sum of all the shortest path distances from u to all \(n-1\) other nodes. Since the sum of distances depends on the number of nodes in the graph, closeness is normalised by the sum of minimum possible distances \(n-1\).

$$\begin{aligned} T_{C} = \dfrac{n-1}{\sum _{v\mathop{=}1}^{n\mathop{-}1}d(v,u)} \end{aligned}$$
(6)

where d(v, u) is the distance of shortest path between v and u, and n is the number of nodes in the graph. (Hagberg et al. 2008)

The current flow closeness centrality \(T_{CFC}\) and edge current flow betweenness centrality \(T_{ECFB}\), or sometimes called random-walk betweenness, considers how often a node falls on a random walk between another pair of nodes. The measure is beneficial for finding vertices of high centrality that do not happen to lie on geodesic paths or on the paths formed by maximum-flow cut-sets (Newman 2005).

The degree centrality \(T_{D}\), also called degree, of a node, equals the number of connecting edges. The degree and its distribution are closely related to network robustness or vulnerability (Barabási and Albert 1999; Albert et al. 2004). The degree centrality considers only the direct neighbours of a node, i.e. it cannot cope with the importance of the connecting nodes.

The eigenvector centrality \(T_{E}\) overcomes such an issue by including the neighbourhood of a node more generally. Instead of the degree, the uth node is characterised by the uth element of the vector x from the equation

$$\begin{aligned} \lambda x_u = \sum _{j\mathop{=}1}^n a_{ij} x_j, u=1,\dots ,n \end{aligned}$$
(7)

where \(\lambda\) is the largest eigenvalue of the adjacency matrix A, \(a_{ij}\) is the element of A from the ith row and jth column. \(a_{ij}\) equals to 1 if there is a connection between the ith and jth node, and 0 otherwise. (Newman 2010)

The Katz centrality \(T_{K}\) generalises the eigenvector centrality. The Katz centrality computes the relative influence of a node within a network by measuring the number of the immediate neighbours (first-degree nodes) and all other nodes in the network that connect to the node under consideration through these immediate neighbours (Hagberg et al. 2008). The Katz centrality for node u

$$\begin{aligned} x_u = \alpha \sum _{j\mathop{=}1}^n a_{ij} x_j + \beta , u=1,\dots ,n \end{aligned}$$
(8)

where \(\alpha\) and \(\beta\) are constants. \(\alpha\) must be smaller than the highest eigenvalue of the adjacency matrix, i.e. \(\alpha <\lambda\), and \(\beta\) controls the initial centrality. If \(\alpha =1/\lambda\) and \(\beta =0\), Katz centrality is the same as eigenvector centrality. During this research, the default values in the NetworkX package are applied, i.e. \(\alpha =0.1\), and \(\beta =1\) (Newman 2010). The values for the constants are arbitrary and can be further researched.

The second order centrality \(T_{SO}\) of a given node is the standard deviation of the return times to that node of a perpetual random walk on the graph (Hagberg et al. 2008). It provides each node locally with a value reflecting its relative criticality and relies on a random walk visiting the network unbiasedly. To this end, each node records the time elapsed between visits of that random walk (called return time in the sequel) and computes the standard deviation (or second-order moment) of such return times (Kermarrec et al. 2011). The lower the second-order centrality is, the higher the actual importance gets, i.e. an inverse relationship is expected between the second-order centrality and the criticality.

Table 1 Topological quantities to estimate the criticality. All metrics are computed with the Python NetworkX package (Hagberg et al. 2008). Since some metrics are defined for nodes, not edges, they need line graph transformation, where links become nodes, and nodes become links
Full size table

4.3 Results and Discussion

Spearman’s rank correlation coefficient is calculated between the topological metrics and the criticality values for 14 real-life WDNs. Besides the topological quantities, the volumetric flow rate is also considered since an isolation valve with a higher flow rate is expected to have a higher criticality. Figure 4 contains all the boxplots. A boxplot represents the correlation coefficients for each network, i.e. each boxplot contains 14 data points. The boxplots are arranged in decreasing order regarding the median value, and the volumetric flow rate is individually presented on the right side.

The flow rate in most networks does not show any significant correlation with criticality, even though it was expected, similarly to (Giustolisi et al. 2019) in the case of pipelines. If an isolation valve transfers a high amount of water during regular operation, it might not be a critical element of the network. WDNs also show negative and positive correlations for most centrality measures, except the Katz and the Degree centrality. Both indicate positive relations to criticality; however, neither is strong enough for a direct approximation. Practically, if the complete evaluation of the criticality is not available (e.g. due to the size of the hydraulic model or lack of model), the Katz or the Degree centrality can be used as a rough estimate for the criticality. It can still provide information about the criticality that can help distribute the resources in maintenance planning.

Although the betweenness centrality might be the most popular topological metric in the field, see (Giustolisi et al. 2022; Simone et al. 2022; Giustolisi et al. 2019), the correlation for most networks is below 0.25. Even the direction of the relationship is not clear, as four networks indicate negative correlations. As expected, the second-order centrality shows negative coefficients; however, their absolute value is lower than the Katz or the Degree centrality.

Fig. 4
figure 4

Spearman’s rank correlation coefficients between the relative average shortfall and different topological metrics. Each boxplot includes data from 14 real-life WDNs

Full size image

The widely used betweenness and closeness centrality cannot estimate the criticality. Moreover, most analysed topological parameters cannot catch the essence of the criticality. However, Katz and Degree centrality show a convincing correlation for most real-life networks. The computational time is negligible for each complex network theory quantity. Since the required input data is only the topology with the pipelines and isolation valve location is necessary, Katz and Degree centrality can be used during the design phase or for operating networks where a calibrated hydraulic model is unavailable.

5 Conclusions

The paper presented the criticality analysis of isolation valves during a random pipe failure and topological estimates avoiding computationally expensive hydraulic simulations. The criticality of a valve is, by definition, the extra relative average shortfall caused by the valve malfunction; that is, it cannot be closed or missing. The nature of the criticality distributions shows a power-law trend, i.e. each network contains a highly exposed isolation valve, which operation is crucial in terms of service vulnerability. During financial planning of the maintenance, it is essential to concentrate the resources on ensuring the operation of such valves to keep the vulnerability of the network as low as possible.

Since the complete evaluation of the criticality analysis is computationally expensive, several topological metrics are introduced. The graph quantities have the advantage regarding CPU time and necessary information, as they do not need a calibrated hydraulic model, only the topology. Although most metrics could not achieve high Spearman’s rank correlation coefficients that can be used for approximation, Katz and Degree centrality show acceptable positive relationships. The correlations are still not strong enough for a direct approximation. However, suppose a hydraulic model or the complete criticality evaluation is not feasible. In that case, they can serve as a first estimate and help distribute the resources for maintenance or support during the planning phase.