Generalized Impedance-based Transient Analysis for Multi-branched Pipeline Systems

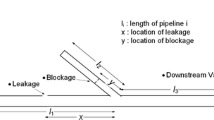
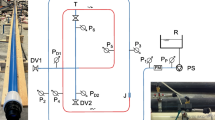
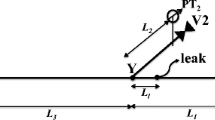
Abstract

Transient analysis of multi-branched pipeline systems is generalized by the development of an impedance method. Both open and closed boundaries of branched pipeline elements were implemented in the analytical development of a reservoir multi-branched pipeline valve system, in which impedance and transient responses performance were compared with those of conventional approaches. To address realistic boundary conditions along the branched element, a partially opened boundary condition was implemented in the impedance expression of the branched pipeline system. The performance of the generalized multi-branch impedance method was evaluated on a large water supply system with 10 minor branches from the actual system. The impact of the designated branches was evaluated using the pressure root-mean-square error (RMSE) and the energy spectral density difference between the original and skeletonized systems. Combinations of multiple branches for certain flow conditions were identified based on the holistic response for both the frequency and time domains. The proposed method can be a useful alternative to effectively address the skeletonization issue for pipeline systems with multi-branched elements.

Appendix

The analytical impedance formulation (AIF) for the unsteady friction model under laminar flow conditions can be developed from existing studies (Brown 1962; Kim 2020). If the boundaries for multi-branched systems are closed, the hydraulic impedance of the nth number of branched pipeline elements can be generalized as follows:

$$\frac{{H}_{3n+1}}{{Q}_{3n+1}}=-{\mathrm{Z}}_{sxn}\frac{{\sum }_{j=1}^{n}\left({\prod_{i=x1}^{yn}{Z}_{si})}_{i\ne j}(\mathrm{tanh}{\Gamma }_{xj}{x}_{j}\right)+\sum_{k=1}^{n}{(\sum_{j=1}^{m1}(\prod_{i=x1}^{xn}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{odd cmb}))}_{k}}{{\prod_{i=x1}^{xn}\left({Z}_{si}\right)}_{3n th}+{\sum_{k=1}^{n}(\sum_{j=1}^{m2}(\prod_{i=x1}^{y2}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{even cmb}))}_{k}}$$

(22)

where the propagation constant is ${\Gamma }_{xj}=s{x}_{j}/({a}_{j}\sqrt{1-2{J}_{1}(\frac{i{D}_{j}}{2\sqrt{\frac{s}{\upsilon }}})/(i{D}_{j}/2\sqrt{\frac{s}{\upsilon }}{J}_{0}(i{D}_{j}/2\sqrt{s/\nu )}}$), and the characteristic impedance is ${Z}_{si}={a}_{i}/(g{A}_{i}\sqrt{1-2{J}_{1}(\frac{i{D}_{i}}{2\sqrt{\frac{s}{\upsilon }}})/(i{D}_{i}/2\sqrt{\frac{s}{\upsilon }}{J}_{0}(i{D}_{i}/2\sqrt{s/\nu )}}$, s is the frequency, ${\mathrm{D}}_{i or j}$ is the diameter of the element number subscript i or j, i is an imaginary unit, and J₀ and J₁ are first-type Bessel functions of the zero and first orders, respectively.

If the boundaries for multi-branched systems are open, the hydraulic impedance can be expressed as follows:

$$\frac{{H}_{3n+1}}{{Q}_{3n+1}}=-{\mathrm{Z}}_{sxn}\frac{\sum_{k=1}^{n}{(\sum_{j=1}^{m1}(\prod_{i=x1}^{xn}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{even cmb}))}_{k}}{{\sum_{k=1}^{n}(\sum_{j=1}^{m2}(\prod_{i=x1}^{y2}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{old cmb}))}_{k}}$$

(23)

and

$$\frac{{H}_{3n+1}}{{Q}_{3n+1}}=-{\mathrm{Z}}_{sxn}\frac{\sum_{k=1}^{n}{(\sum_{j=1}^{m1}(\prod_{i=x1}^{xn}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{odd cmb}))}_{k}}{{\sum_{k=1}^{n}(\sum_{j=1}^{m2}(\prod_{i=x1}^{y2}{\left({Z}_{si}\right)}_{3n th}{\left(\mathrm{tanh}{\Gamma }_{j}{(x or y)}_{j}\right)}_{even cmb}))}_{k}}$$

(24)

for odd and even numbers of upstream branched elements, respectively.

The AIF formulation for the unsteady friction model under turbulent flow conditions can be developed from models of instantaneous accelerations (Brunone et al. 1991; Kim 2020). If the boundaries for multi-branched systems are closed conditions, the hydraulic impedance downstream of the branched pipeline element, subscript db, can be generalized as follows:

$$\frac{{H}_{db}}{{Q}_{db}}=\frac{{Zcx}_{1}{Zcx}_{3}{Zcx}_{6}+{Zcx}_{5}({Zcx}_{2}{Zcx}_{3}-{Zcx}_{1}{Zcx}_{4})}{{Zcx}_{8}{Zcx}_{1}{Zcx}_{8}+{Zcx}_{7}({Zcx}_{2}{Zcx}_{3}-{Zcx}_{1}{Zcx}_{4})}$$

(25)

where ${Zcx}_{1}=-{Z}_{cxu1}{Z}_{cxu2}{e}^{{\Upsilon }_{xu1}{x}_{u}}+{Z}_{cxu1}{Z}_{cxu2}{e}^{{-\Upsilon }_{xu2}{x}_{u}},$ ${Zcx}_{2}={Z}_{cxu2}{e}^{{\Upsilon }_{xu1}{x}_{u}}+{Z}_{cxu1}{e}^{{-\Upsilon }_{xu2}{x}_{u}}$, ${Zxc}_{3}={Z}_{cyb2}{e}^{{\Upsilon }_{yb1}{y}_{b}}+{Z}_{cyb1}{e}^{{-\Upsilon }_{yb2}{y}_{b}}$, ${Zcx}_{4}={e}^{{\Upsilon }_{yb1}{y}_{b}}-{e}^{{-\Upsilon }_{yb2}{y}_{b}}$, ${Zcx}_{5}=-{Z}_{cxd1}{Z}_{cxd2}{e}^{{\Upsilon }_{xd1}{x}_{d}}+{Z}_{cxd1}{Z}_{cxd2}{e}^{{-\Upsilon }_{xd2}{x}_{d}}$, ${Zcx}_{6}={Z}_{cxd1}{e}^{{\Upsilon }_{xd1}{x}_{d}}+{Z}_{cxd2}{e}^{{-\Upsilon }_{xd2}{x}_{d}}$, ${Zcx}_{7}={Z}_{cxd2}{e}^{{\Upsilon }_{xd1}{x}_{b}}+{Z}_{cxd1}{e}^{{-\Upsilon }_{xd2}{x}_{b}}$, and ${Zcx}_{8}={e}^{{\Upsilon }_{xd1}{x}_{d}}-{e}^{{-\Upsilon }_{xd2}{x}_{d}}$. Here, the propagation constants ${\Upsilon}_{l1}$ and ${\Upsilon}_{l2}$ can be defined as ${\Upsilon}_{l1, l2}=(\mp mCs+\sqrt{(mCs{)}^{2}+4({s}^{2}CL+RCs)})/2$; $\mathrm{m}={(a}_{l}{k}_{2})/(2g{A}_{l})$; the capacitance as $C=(g{A}_{l})/{{a}_{l}}^{2}$; the inertance as $\mathrm{L}=(1+{k}_{1})/(g{A}_{l})$; the resistance per unit length as $R=(f\overline{Q })/(g{D}_{l}{{A}_{l}}^{2})$ for turbulent flow; and the characteristic impedances as ${Z}_{cl1},{Z}_{cl2}=\frac{{\Upsilon }_{l1}}{Cs},\frac{{\Upsilon }_{l2}}{Cs}$ where subscript l represents corresponding pipeline elements (e.g., xu, xd, and yb represent the upstream section, downstream section, and branched element, respectively).

If the boundaries for multi-branched systems are open conditions, the downstream hydraulic impedance of the branched pipeline element, subscript db, can be generalized as follows:

$$\frac{{H}_{db}}{{Q}_{db}}=\frac{{Zox}_{1}{Zox}_{3}{Zox}_{6}+{Zox}_{5}({Zox}_{2}{Zox}_{3}-{Zox}_{1}{Zox}_{4})}{{Zox}_{8}{Zox}_{1}{Zox}_{8}+{Zox}_{7}({Zox}_{2}{Zox}_{3}-{Zox}_{1}{Zox}_{4})}$$

(26)

where ${Zox}_{1}=-{Z}_{cxu1}{Z}_{cxu2}{e}^{{\Upsilon }_{xu1}{x}_{u}}+{Z}_{cxu1}{Z}_{cxu2}{e}^{{-\Upsilon }_{xu2}{x}_{u}}$, ${Zox}_{2}={Z}_{cxu2}{e}^{{\Upsilon }_{xu1}{x}_{u}}+{Z}_{cxu1}{e}^{{-\Upsilon }_{xu2}{x}_{u}}$, ${Zoc}_{3}={{Z}_{cyb1}Z}_{cyb2}{e}^{{\Upsilon }_{yb1}{y}_{b}}-{{Z}_{cyb1}Z}_{cyb2}{e}^{{-\Upsilon }_{yb2}{y}_{b}}$, ${Zox}_{4}={Z}_{cyb1}{e}^{{\Upsilon }_{yb1}{y}_{b}}+{Z}_{cyb2}{e}^{{-\Upsilon }_{yb2}{y}_{b}}$, ${Zox}_{5}=-{Z}_{cxd1}{Z}_{cxd2}{e}^{{\Upsilon }_{xd1}{x}_{d}}+{Z}_{cxd1}{Z}_{cxd2}{e}^{{-\Upsilon }_{xd2}{x}_{d}}$, ${Zox}_{6}={Z}_{cxd1}{e}^{{\Upsilon }_{xd1}{x}_{d}}+{Z}_{cxd2}{e}^{{-\Upsilon }_{xd2}{x}_{d}}$, ${Zox}_{7}={Z}_{cxd2}{e}^{{\Upsilon }_{xd1}{x}_{b}}+{Z}_{cxd1}{e}^{{-\Upsilon }_{xd2}{x}_{b}}$, and ${Zox}_{8}={e}^{{-\Upsilon }_{xd2}{x}_{d}}-{e}^{{\Upsilon }_{xd1}{x}_{d}}$.

Further formulations to multiple downstream branches and main sections can be developed from Eqs. (25) and (26).