1 Introduction

Soil water-driven properties are basic requirements for water balance in irrigation and drainage, leaching requirements of salts, water supply for plants, and other agronomical and natural applications (Fredlund et al.1997; Rousseva et al. 2017). The soil water holding capacity (WHC) is a key parameter in hydrological modeling for imparting the difference between surface and base flow. The available water for different soils i.e. the amount of water stored between soil moisture at the suction of 15 bar (PWP) and the suction of 0.33 bar (FC) is conducive for precision irrigation. The measurement of soil water retention requires sophisticated instruments, and skilled manpower (Wosten et al. 2001) hence some alternative methods/models are essential (Rawls et al. 1991; Qi et al 2018) for developing countries like India.

Zhang and Han (2019) analyzed the impact of different concentrations of feldspathic sandstone (T1 as 1:5, T2 as 1:2, and T3 as 1:1) on aeolian sandy soil in the form of changing soil texture and concluded that van Genuchten's model worked well to replicate SWR. The hydraulic properties like texture, organic carbon, and pore spaces (Bronick and Lal 2005; Alaoui et al 2011) along with climatic factors like temperature, wind, and humidity have a major role to define the amount of water infiltrating the ground, retained in the soil and returned to stream as base flow (Hu et al 2009). The soil characteristics and organic compounds are the basic properties that govern soil water retention (Rasyid et al. 2017) and most of the pedotransfer equations developed in the past used soil texture and percentage carbon. However, Srivastava et al. (2021) applied Bucket Grassland Model (BGM) to understand the effect of different parameters on soil moisture variation in different landscapes and found that it is more sensitive to topography and climate. Chen et al. (2014) used the HYDRUS-1D model to investigate soil moisture dynamics in two different catchments for hydrological modeling. Wang et al (2017) proposed two different PTFs for van Genuchten’s model using basic gradation parameters of size from which 60% of soil particles passed (d60) and uniformity coefficient (Cu) having an advantage of better results despite fewer parameters. Apart from pedotransfer function and analytical models, the artificial neural network, fuzzy and adaptive neuro-fuzzy inference systems (ANFIS), and other artificial techniques can be used for modeling the soil water retention process and other experimental data (Sihag et al. 2019; Angelaki et al. 2021; Salmasi et al. 2021). The ANFIS is the framework intended to reproduce how the human mind breaks down and measures data. Furthermore, Kumar et al. (2014) applied the ANFIS technique for the assessment of evaporation from the pan, and different researchers used it for rainfall-runoff modeling (Belvederesi et al. 2020; Ehteram et al. 2019; Talei et al. 2010; Nourani and Komasi 2013; etc.). Besides this, ANFIS has been used for other fields, e.g., daily average wind power interval (Zhang et al. 2016), short-term wind speed (Zhang et al. 2017), sustainability performance (Nilashi et al. 2018), greenhouse gas emissions (Alhindawi et al. 2019), and proton exchange membrane fuel cells (Wilberforce and Olabi 2020).

From the literature review on different modeling techniques, it has been observed that the PTFs are commonly used due to simplicity, but ANFIS is now being progressively used for characterizing the SWR process. The pedotransfer functions due to their empirical nature have limited regional applicability and cannot be applied universally. On the other hand, soft computing techniques have the tolerance for error, reasoning ability, regionalizing the processes with greater flexibility in applications, and can provide accurate results. In the present study, a comparative analysis was made to evaluate the performance of both these techniques for m soil water retention characteristics which are useful to assess the appropriate amount of water needed to supply in the command for optimal production besides understanding drainage and leaching phenomenon.

2 Materials and Methods

2.1 Study Area and Data Used

Two adjoining irrigation commands of Benisagar and Rangawan reservoirs situated in the Madhya Pradesh state of India were considered for the present study having wheat and gram in rabi and soybean in kharif seasons as principal crops. The depth-integrated soil samples (0 to 90 cm) from eleven sites have been collected from different sites to cover the spatial distribution of soils and analyzed for soil water retention using the pressure plate apparatus. The soil moisture after applying different suction pressure was determined and used in the analysis. The textural analysis was conducted for coarse and fine particles in the soil along with the determination of organic carbon in these soils. The location map and soil sampling points in the commands were given in Fig. 1.

Fig. 1
figure 1

Location map and sample sites in the commands of Benisagar and Rangawan reservoirs in India, a. Location map, b. Sites for collection of soil samples

Full size image

2.2 Methodology

The fundamental hypothetical models of unsaturated flow generally depend on the distorted depiction of medium pores as a load of round and hollow formed vessels and expect that water pressure head in the soil is attributed to slender powers just and dismisses the forces due to adsorptive surface (Jaiswal et al 2020). Subsequently, it is regularly expected that the fluid stream is irrelevant when the soil is closed or at the residual moisture content (θr). To represent effective saturation, the given equation is called the Mualem equation (Mualem 1976).

$${S}_{e}=\frac{\theta -{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}$$
(1)

Here, Se is effective saturation ranges from 0 to 1, \(\theta\) is the volumetric soil moisture at suction pressure h, \({\theta }_{s}\) and \({\theta }_{r}\) are saturated and residual soil moisture content respectively. Soil water retention in the field can be obtained either by collecting field samples and laboratory analysis or by using the pedotransfer function where easily known soil properties can be used to compute soil moisture at different pressure heads (Ghanbarian-Alavijeh and Liaghat 2009). Fitting the soil suction pressure with soil moisture, Brooks and Corey (1964) suggested the following to relate the effective water saturation with suction pressure (h) and air entry pressure head (hd)

$$\frac{\theta -{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}= \left[\begin{array}{c}{\left(\frac{h}{{h}_{d}}\right)}^{\lambda }\\ 1, h<{h}_{d}\end{array},h>{h}_{d}\right.$$
(2)

Brooks & Corey is the simplest and most commonly used model but is unable to represent the whole range of soil suction pressure (Sillers et al 2001) and hence van Genuchten (1980) simply represented the Mualem equation with the help of two non-dimensional parameters m and n by the following equation

$$\frac{\theta -{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}= {[1+{\left(\alpha h\right)}^{n}]}^{-m}$$
(3)

where, \(\alpha\) is a pore size-related parameter, while n is the dimensional less constant depending on texture (pore size distribution), and m is another dimension less constant. A fixed relationship of m = (1–1/n) was suggested and the equation can be expressed as

$$\frac{\theta -{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}= \frac{1}{{[1+{\left(\alpha h\right)}^{n}]}^{(1-\frac{1}{n})}}$$
(4)

In India, the soil water retention (SWR) properties are not commonly accessible and Patil et al (2013) referenced the non-accessibility of information in the black soil region and applied pedotransfer function, artificial neural network (ANN) and k nearest neighbor (kNN) approaches. Pan et al (2019) compared Brook & Corey, van Genuchten, and Gardner’s models (\(\theta =\frac{1}{1+\alpha {\varphi }^{n}}\), where \(\varphi\) is suction pressure) for soil water retention properties (Gardner 1970) and found that the first two models perform better than the Gardner model in terms of adjusted coefficient of determination while no significant change was found in all three models during degradation. In the absence of the availability of test data, several pedotransfer functions to relate textural characteristics with soil water retention have been suggested in the past by researchers and presented in Table 1.

Table 1 Soil properties used in the development of PTFs based models (Guber 2010)
Full size table

The pressure plate apparatus was used to compute soil moisture at different suction pressures. The apparatus contains a membrane system where different suction pressure ranging from 0.1 to 15 bar can be applied to determine moisture retention through the measurement of volumetric/gravimetric moisture content. This apparatus is useful to eliminate moisture from soil samples under controlled applied pressure required throughout the plant growth period. The USDA system of soil texture classification was used to define the type of soil based on percentages of clay, silt, loam, and sand. In the investigation, pedotransfer and ANFIS based models were applied for assurance of best-fit models from collected data.

2.2.1 Pedotransfer Function (PTF) Based Models

The CalcPTF (Calc PedoTransfer Functions) (Guber and Pachepsky 2010) was used to fit PTF-based models (Brooks & Corey and van Genuchten models) on different sites for computation of the range of soil moisture retention (Pachepsky and Rawls 2004; Patil and Singh 2016). The CalcPTF software was used in the analysis to fit seven models to fit Brooks and Corey’s equation using PTFs suggested by Oosterveld and Chang 1980 (P-BC-OC), Saxton et al. 1986 (P-BC-SEL), Campbell and Shiosawa 1992 (P-BC-CS), Williams et al. 1992 (P-BC-WEL1 and P-BC-WEL2) and Mayr and Jarvis 1999 (P-BC-MJ) and remaining nine are based on van Genuchten equation suggested by Gupta and Larson 1979 (P-VG-GL), Wösten et al. 1999 (P-VG-WOEL1), Wösten et al. 1999 (P-VG-WOEL2) and Tomasella and Hodnett 1998 (P-VG-TH).

2.2.2 ANFIS Based Model for Soil Water Retention and Sensitivity Analysis

The fundamental of the ANFIS approach is the data powered by the fuzzy simulation method. This is a three-component rule-based method: membership functions of the input and output variables, fuzzy principles, output features, and outcomes (Naderloo et al. 2012). ANFIS contains a structure of the feed-forward neural network (FFNN) where each layer represents a component of the neuro-fuzzy system (NFS). In ANFIS, two learning techniques are commonly used to define the relationship between input and output to evaluate the optimized distribution of membership tasks (Fig. 2A). Propagation and hybrid are these learning approaches. The fuzzy logic toolbox of the MATLAB version (R2019a) was used to build FIS using ANFIS. The number of input variables was four, and the SWR is also regarded as the ANFIS model output under different pressures. It has the membership function forms of output (linear or constant), methods of optimization (hybrid or backpropagation), and the epochs number (Polykretis et al. 2019; Bajirao et al. 2021). The type of membership function (MF) was Gumbel and linear for the input and output, respectively. The number of epochs was 100 and the learning method was hybrid. The ANFIS has some advantages, including the ability to capture the nonlinear structure of a process, adaptation capability, and rapid learning capacity (Lotfi et al. 2016; Srisaeng et al. 2015; Panapakidis and Dagoumas 2017; Prasad et al. 2016; Zafarani et al. 2005). The detailed functioning of the ANFIS structure is obtained in the literature by Bajirao et al. (2021). In addition, flowchart for implementing the study work is presented in Sensitivity analysis is an analysis technique that works on the basis of what-if analysis like how independent factors can affect the dependent factor and is used to predict the outcome when analysis is performed under certain conditions. Best subsets regression, an exploratory model building regression analysis was used in this study for estimating the best input-variables in SWR estimation under different pressures (Fig. 3). It compares all possible models that can be created based upon an identified set of predictors.

Fig.2
figure 2

A The structure of the ANFIS network (Sahin and Erol 2017), B Flowchart for modelling SWR based on PTF and ANFIS models

Full size image
Fig.3
figure 3

Sensitivity analysis of SWR parameters under different pressures

Full size image

2.2.3 Performance Evaluation of Models

The performance evaluation of different PTF and ANFIS-based models were computed using root mean square error (RMSE), coefficient of determination (R2), and adjusted R2. The RMSE indicates the difference between observed and modelled results and any value near zero may be considered the best match. The adjusted R2 reflects the coefficient of correlation considering the number of parameters of the model on performance and investigated the degree of correlation between observed and predicted values, which can take any value ≤ 1 indicating a better fit (Neter et al. 1996). The equations for the computation of different performance evaluators can be seen in the literature (Elbeltagi et al. 2020a, b, c, d).

The major disadvantage of PTF based modeling approach lies in the development of a separate model for each site and hence cannot be replicated on other sites. On the other hand, ANFIS-based models used data from multiple sites and can be used on other sites but need knowledge of advanced computing techniques and programming languages.

3 Results and Discussion

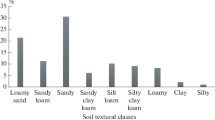
The soil samples from eleven different sites were collected and analyzed for textural analysis, organic carbon, bulk density, and soil water retention testing, and found that the soils in the commands are silty loam (Table 2). After determining soil moisture at different suction pressures, PTF-based models were applied and ANFIS based model was developed and compared using the goodness of fit measures like root mean square error (RMSE), Nash Sutcliffe efficiency (NSE), coefficient of determination (R2), mean annual percentage error (MAPE), etc.

Table 2 Location of soil sampling sites and results of textural analysis
Full size table

3.1 Results of PTF Based Models

Various PTF based models explained in the methodology part were fitted for each site and different goodness of fit parameters was determined. From the analysis, it was found that Rawls and Brakensiek's 1985 model performed the best for site-1, 2, 5, 6, 10, and 11, Saxton et al 1986 for site-3 and 9, Tomasella and Hodnett 1998 for site-4 and 7and Campbell and Shiosawa 1992 for site-8. The best-fit model based on Nash Sutcliffe efficiency and RMSE is presented in Table 3 and found that Brook and Corey's equation is the most suited model for most of the sites in the command. The measured and computed PTFs-based SWRs on different sites matched closely and the correlation for different sites ranged from 0.93 (Site-4) to 0.99 (Site-6, 7, 9, 11).

Table 3 Best-fit PTFs based models and their parameters
Full size table

3.2 Results of the ANFIS Model

To model soil water retention at different pressures, the input variables of the ANFIS model were the percentages of gravel, sand, silt, clay, and SWR at different suction pressures. Figure 4 showed the relationship between the number of epochs and ANFIS network training error and it can be noticed that after two ANFIS training and testing, the error is decreased as the number of epochs increases from 1 to 100 and that finally levels off. After implementing the modeling process by the ANFIS model, the outputs generated proved well with the observed SWR values as shown in Fig. 5. From the analysis, it is clear that the proposed ANFIS model is capable to model regional (when results of all sites were combined) as well as at-site soil water retention. The linear regression correlation coefficient, slope, and intercept were found to be 1.00, 0.999, and 0.001, respectively. Moreover, the lowest and highest variations for all developed ANFIS models varied from -0.03 to 0.08, -0.01 to 0.02, -0.04 to 0.15, -0.02 to 0.03, -0.02 to 0.02, -0.02 to 0.03, -0.01 to 0.02, -0.01 to 0.02, -0.02 to 0.03, and -0.03 to 0.04 at the different pressures from 0.1 to 15 bar. Furthermore, the performance metrics of MSE, MAE, and MARE reached nearly zero for most of the ANFIS models. Also, the mean absolute percentage error (MAPE) achieved the lowest and highest values of 0.00, and 0.02 (Table 4). The radar chart depicting the performance of SWR in terms of RMSE, MAPE, MAE, MARE, and NSE is presented in Fig. 6. Perecentage of uncertainty was as follows: 1, 2.94, 1.61, 1.49,1.23, 1.03, 0.98, 1, 0.98 and 1% for different ANFIS models under 0.1, 0.3, 0.5, 0.7, 1, 3, 5, 7, 10 and 15 BAR, respectively.

Fig.4
figure 4

The relation between ANFIS training errors (bar) and the epoch’s number in (A) training and (B) ANFIS testing

Full size image
Fig. 5
figure 5

Scatter plot of measured and predicted SWR at different suction pressures (a) 0.1 bar, (b) 0.33 bar, (c) 0.5 bar, (d) 0.7 bar, (e) 1 bar, (f) 3 bar, (g) 5 bar, (h) 7 bar, (i) 10 bar, (j) 15 bar

Full size image
Table 4 Comparison of performance of ANFIS and PTF models
Full size table
Fig. 6
figure 6

Radar chart showing SWR prediction performance (a) RMSE, (b) MAPE, (c) MAE, (d) MARE, and (e) NSE

Full size image

3.3 Comparison of PTF and ANFIS Based Models

The PTF based multiple models and the ANFIS model were compared and found that although PTF based models work well, the ANFIS model replicates the observed SWR exactly and displayed efficiency near 1. PTF-based applications found separate best-fitted models for different sites and no single PTF can be used unanimously all over the region. This limitation can be overcome by the application of ANFIS models which can be used at any point in the region using sand, silt, and clay percentage only. The ANFIS models gave high performance and accuracy compared to Fashi et al. (2019) who found a correlation coefficient of 0.88. As well, the outcomes of ANFIS models are very well in comparison with Fashi (2016), who computed a correlation of 0.55 using combinations of sand, silt, and clay for modeling soil water retention. In the digital era, ANFIS based model can be used in any command of the region using soil texture to determine irrigation scheduling, irrigation demand, and drainage planning. The measured and computed SWR from PTF and ANFIS models for a few sites are presented in Fig. 6 indicating that the ANFIS model predicts the measured SWR well, on the other hand, PTF predicts the SWR on the higher side. The ANFIS method applied in the study yielded efficiency near to one which was higher than the PTF-based assessment where it ranged from 0.73 to 0.91. The ANFIS model has the advantage of regional estimation of SWR properties which is not possible with PTF based modeling (Fig. 7).

Fig. 7
figure 7

Comparison of PTF, ANFIS, and measured SWR for few sites in the commands

Full size image

4 Conclusions

Field experiment-based SWR computations require costly field experiments and can’t be done on different soils on a regional scale. Alternatively, pedotransfer functions are used to compute these characteristics using physical properties of soil readily available having a higher margin of error due to its empirical nature. The proposed adaptive neuro-fuzzy inference systems (ANFIS) approach proposed has given better Nash-Sutcliff efficiency (nearly 1) as compared to PTFs (0.73 to 0.91). Easily available soil properties like sand, silt, and clay percentages can be used to estimate soil water retention. The proposed ANFIS model's estimated field capacity and permanent wilting point are utilized to predict irrigation water amounts and design drainage to remove excess water, making the research directly applicable in the field. The AFIS-based model proposed in the investigation showed the potential to reproduce the soil water retention qualities on local as well as regional scales.