Parameter Estimation for Univariate Hydrological Distribution Using Improved Bootstrap with Small Samples

Abstract

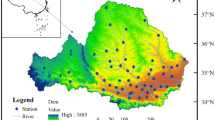
It is crucial yet challenging to estimate the parameters of hydrological distribution for hydrological frequency analysis when small samples are available. This paper proposes an improved Bootstrap and combines it with three commonly used parameter estimation methods, i.e., improved Bootstrap with method of moments (IBMOM), maximum likelihood estimation (IBMLE) and maximum entropy principle (IBMEP). A series of numerical experiments with different small sized (10, 20, and 30) of samples generated from the three commonly used probability distributions, i.e., Pearson Type III, Weibull, and Beta distributions, are conducted to evaluate the performance of the proposed three methods compared with the cases of conventional Bootstrap and without-Bootstrap. The proposed methods are then applied to the estimation of distribution parameters for the average annual precipitations of 8 counties in Qingyang City, China with assumption of Pearson Type III distribution for the average annual precipitations. The resulting absolute deviation (AD) box plots and Root Mean Square Error (RMSE) and bias estimators from both the numerical experiments and the case study show that the estimated parameters obtained by the improved Bootstrap methods have less deviation and are more accurate than those obtained through conventional Bootstrap and without-Bootstrap for the three distributions. It is also interestingly found that the improved Bootstrap provides more relative improvement on the parameter estimation when smaller size of sample is used. The method based on improved Bootstrap paves a new way forward to alleviating the need of large size of sample for quality hydrological frequency analysis.

Appendices

Appendix A: Distribution Functions

1.1 Pearson Type III Distribution

It contains three parameters $\alpha ,\beta ,a_{0}$ with the following probability density:

$$f(x) = \frac{{\beta^{\alpha } }}{\Gamma (\alpha )}(x - a_{0} )^{\alpha - 1} e^{{ - \beta (x - a_{0} )}}$$

(8)

where $\alpha$ is the shape parameter, $\beta$ is the scale parameter, and $a_{0}$ is the position parameter; $x > a_{0}$, $\beta > 0$; $\Gamma (\alpha ) = \int_{0}^{\infty } {t^{\alpha - 1} e^{ - t} dt}$.

The distribution function of the Pearson Type III distribution has the following form:

$$F(x) = \int_{{a_{0} }}^{x} {\frac{{\beta^{\alpha } }}{\Gamma (\alpha )}(t - a_{0} )^{\alpha - 1} e^{{ - \beta (t - a_{0} )}} } dt$$

(9)

1.2 Weibull Distribution

This paper studies the latter two-parameter estimation problem with the following probability density function.

$$f(x) = \frac{a}{b}(\frac{x}{b})^{a - 1} e^{{ - (\frac{x}{b})^{a} }}$$

(10)

where $a$ is the shape parameter and $b$ is the scale parameter; $a > 0$, $b > 0$.

The distribution function of the Weibull distribution has the following form:

$$F(x) = e^{{ - (\frac{x}{b})^{a} }}$$

(11)

The Weibull is a two-parameter distribution that can be considered as an inverse generalized extreme value distribution.

1.3 Beta Distribution

Its probability density function containing two parameters $a,b$ is shown as follows.

$$f(x) = \frac{\Gamma (a + b)}{{\Gamma (a)\Gamma (b)}}x^{a - 1} (1 - x)^{b - 1}$$

(12)

where the range of parameters is $a > 0$, $b > 0$ and $0 < x < 1$, $a,b$ are called shape parameters.

The distribution function of the Beta distribution has the following form:

$$F(x) = \frac{\Gamma (a + b)}{{\Gamma (a)\Gamma (b)}}\int_{0}^{x} {t^{a - 1} (1 - t)^{b - 1} } dt$$

(13)

Appendix B: Parameter Estimation Methods

2.1 Method of Moments (MOM)

• 1. MOM for Pearson Type III distribution is as follows:

$$\left\{ \begin{array}{l} \overline{x} = \alpha \beta + a_{0} \hfill \\ \sigma^{2} (x) = \alpha^{2} \beta \hfill \\ C_{s} = \frac{2}{\sqrt \beta } \hfill \\ \end{array} \right.$$

(14)

• 2. MOM for Weibull distribution is as follows:

  $$\left\{ \begin{array}{l} \overline{x} = b\Gamma (1 + \frac{1}{a}) \hfill \\ \sigma^{2} (x) = b^{2} \Gamma (1 + \frac{2}{a}) \hfill \\ \end{array} \right.$$

  (15)

• 3. MOM for Beta distribution is as follows:

  $$\left\{ \begin{array}{l} \overline{x} = ab \hfill \\ \sigma^{2} (x) = a^{2} b \hfill \\ \end{array} \right.$$

  (16)

  where $x$ is the original sample sequence, $\alpha ,\beta ,a_{0}$ is the parameters to be estimated for the Pearson Type III distribution, which are shape, scale and location parameters, respectively, and which used the first three orders of sample moments $\overline{x},\sigma^{2} (x),C_{s}$, i.e., mean, variance and skewness coefficients to build a ternary system of equations; $a,b$ is the two parameters to be estimated for the Weibull and Beta distributions.

2.2 Maximum Likelihood Estimation (MLE)

• 1. MLE for Pearson Type III Distribution is as follows:

$$\begin{aligned} \ln L(x;\alpha ,\beta ,a_{0} ) & = - n\ln \alpha - n\ln \Gamma (\beta ) + (\beta - 1)\sum\limits_{i = 1}^{n} {\ln (x_{i} - a_{0} )} \\ & \quad - n(\beta - 1)\ln \alpha - \frac{1}{\alpha }\sum\limits_{i = 1}^{n} {\ln (x_{i} - a_{0} )} \\ \end{aligned}$$

(17)

$$\left\{ \begin{gathered} \frac{n\beta }{\alpha } = \frac{1}{{\alpha^{2} }}\sum\limits_{i = 1}^{n} {(x_{i} - a_{0} )} \\ n\psi (\beta ) + n\ln \alpha = \sum\limits_{i = 1}^{n} {\ln (x_{i} - a_{0} )} \\ (\beta - 1)\sum\limits_{i = 1}^{n} {(\frac{1}{{x_{i} - a_{0} }})} = \frac{n}{\alpha } \\ \end{gathered} \right.$$

(18)

• 2. MLE for Weibull distribution is as follows:

  $$\ln L(x;a,b) = n\ln (\frac{a}{b}) + (a - 1)\sum\limits_{i = 1}^{n} {\ln (\frac{{x_{i} }}{b})} - \sum\limits_{i = 1}^{n} {(\frac{{x_{i} }}{b})^{a} }$$

  (19)
  $$\left\{ \begin{array}{l} \frac{1}{a} = \frac{{\sum\limits_{i = 1}^{n} {x_{i}^{a} \ln x_{i} } }}{{\sum\limits_{i = 1}^{n} {x_{i}^{a} } }} - \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln x_{i} } \hfill \\ b^{a} = \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{i}^{a} } \hfill \\ \end{array} \right.$$

  (20)

• 3. MLE for Beta distribution is as follows:

  $$\ln L(x;a,b) = n\ln \Gamma (a + b) - n\ln \Gamma (a) - n\Gamma (b) + \sum\limits_{i = 1}^{n} {\ln (x_{i}^{a - 1} (1 - x_{i} )^{b - 1} )}$$

  (21)
  $$\left\{ \begin{array}{l} \frac{\partial [\ln \Gamma (a)]}{{\partial (a)}}{ - }\frac{\partial [\ln \Gamma (a + b)]}{{\partial (a)}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln x_{i} } \hfill \\ \frac{\partial [\ln \Gamma (b)]}{{\partial (b)}}{ - }\frac{\partial [\ln \Gamma (a + b)]}{{\partial (b)}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln (1 - x_{i} )} \hfill \\ \end{array} \right.$$

  (22)

  where $\Gamma ( \cdot )$ and $\psi ( \cdot )$ are the gamma function and the Pusey function, respectively, and the expression of the relationship between them is that,

  $$\begin{aligned} \psi (x) & { = }\int_{0}^{\infty } {[\frac{{e^{ - t} }}{t} - \frac{{e^{ - xt} }}{{1 - e^{ - t} }}]} dt \\ & = \frac{d}{dx}\ln \Gamma (x) = \frac{{\Gamma^{\prime}(x)}}{\Gamma (x)} \\ \end{aligned}$$

  (23)

  where $x$ must satisfy ${\text{Re}} (x) > 0$, i.e., the real part of each sample is greater than 0.

2.3 Maximum Entropy Principle (MEP)

Based on the book "Entropy-based Parameter Estimation in hydrology" by Singh of Louisiana State University (1998), the derivation of the maximum entropy estimates for the three distributions involved in this paper is given below.

• 1. MEP for Pearson Type III distribution is as follows:

$$\left\{ {\begin{array}{*{20}c} {\overline{x} = \alpha \beta + a_{0} } \\ {\sigma^{2} (x) = \alpha^{2} \beta } \\ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\ln (x_{i} - c)} { = }\psi (\beta ) + \ln \alpha } \\ \end{array} } \right.$$

(24)

• 2. MEP for Weibull distribution is as follows:

  $$\left\{ \begin{array}{l} b^{a} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln x_{i}^{a} } \hfill \\ \psi (1) - \ln b = \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln x_{i} } \hfill \\ \end{array} \right.$$

  (25)

• 3. MEP for Beta distribution is as follows:

  $$\left\{ \begin{array}{l} \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln x_{i} } = \psi (a) - \psi (a + b) \hfill \\ \frac{1}{n}\sum\limits_{i = 1}^{n} {\ln (1 - x_{i} )} = \psi (b) - \psi (a + b) \hfill \\ \end{array} \right.$$

  (26)

The significance of each parameter in the Eqs. (24) to (26) of this section has been described in detail in the previous two subsections.

Appendix C: Empirical Analysis

Fig. 9

P-P plots of the EFC and TFC using unexpanded and expanded data in the Huanxian County

Fig. 10

P-P plots of the EFC and TFC using unexpanded and expanded data in the Qingcheng County

Fig. 11

P-P plots of the EFC and TFC using unexpanded and expanded data in the Zhenyuan County

Fig. 12

P-P plots of the EFC and TFC using unexpanded and expanded data in the Huachi County

Fig. 13

P-P plots of the EFC and TFC using unexpanded and expanded data in the Nianxian County