Joint-Probabilistic Double-Sided Random Interval Programming for Booster Optimization in Water Distribution Network

Abstract

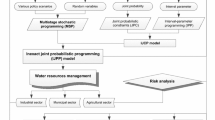
In this paper, a joint-probabilistic double-sided random interval chance-constrained programming (JDRICCP) model was proposed to deal with the random and interval uncertainties in both sides of the constraints and nodal joint probability in booster cost optimization of water distribution system (WDS). The JDRICCP model was applied to two Cases to verify the efficiency of the method on the booster cost optimization under uncertainty. After formulating the JDRICCP model, the booster costs under various violation levels based on four nodal importance measures can be obtained for two Cases. The results indicated that the booster costs are only affected by lower violation probability, and decreased with the rise of violation levels. In addition, the booster costs are closely related to the nodal importance measures. By comparing the booster costs under random interval variables and random variables, the results indicated that under random interval variables the booster costs are less than that under random variables. The results obtained can provide more information for managers to make boosters schemes under dual uncertainties of random and interval.

Appendix I

1.1 Theorem 1

The inequity relationship ${\boldsymbol{A}}(\omega ){x}_{i}^{\pm }\le {\boldsymbol{B}}(\omega )$ is equivalent to ${{\boldsymbol{A}}}^{{\boldsymbol{L}}}(\omega ){x}_{i}^{\pm }\le {{\boldsymbol{B}}}^{{\boldsymbol{R}}}(\omega )$.

1.2 Proof

For any $\lambda \left(0\le \lambda \le 1\right)$, we can have Eqs. (A1) and (A2) expressed as follows.

$$\lambda {A}^{L}\left(\omega \right)+\left(1-\lambda \right){A}^{R}\left(\omega \right) \epsilon {\boldsymbol{A}}(\omega )$$

(A1)

$$\lambda {B}^{L}\left(\omega \right)+\left(1-\lambda \right){B}^{R}\left(\omega \right) \epsilon {\boldsymbol{B}}(\omega )$$

(A2)

Then, for any $\omega$ we can obtain Eqs. (A3) and (A4) expressed as follows.

$${A}^{L}(\omega ){x}_{i}^{\pm }\le \lambda {A}^{L}\left(\omega \right){x}_{i}^{\pm }+\left(1-\lambda \right){A}^{R}\left(\omega \right){x}_{i}^{\pm }\le {A}^{R}\left(\omega \right){x}_{i}^{\pm }$$

(A3)

$${B}^{L}\left(\omega \right)\le \lambda {B}^{L}\left(\omega \right)+\left(1-\lambda \right){B}^{R}\left(\omega \right)\le {B}^{R}\left(\omega \right)$$

(A4)

Moreover, when ${x}_{i}^{\pm }\ge 0$ we can have Eq. (A5) expressed as follows.

$$\begin{aligned}\left\{\omega |{A}^{L}\left(\omega \right){x}_{i}^{\pm }\le {B}^{R}(\omega )\right\}&\supseteq \left\{\omega |\lambda {A}^{L}\left(\omega \right){x}_{i}^{\pm }+\left(1-\lambda \right){A}^{R}\left(\omega \right){x}_{i}^{\pm }\le \lambda {B}^{L}\left(\omega \right)+\left(1-\lambda \right){B}^{R}\left(\omega \right)\right\}\\&\supseteq \left\{\omega |{A}^{R}\left(\omega \right){x}_{i}^{\pm }\le {B}^{L}(\omega )\right\}\end{aligned}$$

(A5)

As such, we can obtain Eq. (A6) expressed as follows.

$$\begin{aligned}Pr\left\{\omega |{A}^{L}\left(\omega \right){x}_{i}^{\pm }\le {B}^{R}(\omega )\right\}&\ge Pr\left\{\omega |\lambda {A}^{L}\left(\omega \right){x}_{i}^{\pm }+\left(1-\lambda \right){A}^{R}\left(\omega \right){x}_{i}^{\pm }\le \lambda {B}^{L}\left(\omega \right)+\left(1-\lambda \right){B}^{R}\left(\omega \right)\right\}\\&\ge Pr\left\{\omega |{A}^{R}\left(\omega \right){x}_{i}^{\pm }\le {B}^{L}(\omega )\right\}\end{aligned}$$

(A6)

hence, $Pr\left\{\omega |{\boldsymbol{A}}\left(\omega \right){x}_{i}^{\pm }\le {\boldsymbol{B}}(\omega )\right\}$ can be replaced by $Pr\left\{\omega |{A}^{L}\left(\omega \right){x}_{i}^{\pm }\le {B}^{R}(\omega )\right\},$ i.e., ${A}^{L}\left(\omega \right)$ and ${B}^{R}(\omega )$ extend the feasible sets.

1.3 Theorem 2

The inequity relationship ${\boldsymbol{A}}(\omega ){x}_{i}^{\pm }\ge {\boldsymbol{B}}(\omega )$ is equivalent to ${A}^{R}(\omega ){x}_{i}^{\pm }\ge {B}^{L}(\omega )$.

1.4 Proof

The proof of this theorem is the same as Theorem 2.