1 Introduction

Worldwide groundwater demand for irrigation is increasing due to diminishing and variable surface water supplies that stress aquifer systems (Richey et al. 2015). For this reason it is important to assess how food production, aquifers and their feedback respond to water policies and economic and crop production changes. Models used to understand these relationships have intrinsic uncertainties in their input and calibration parameters. In order to develop better informed modeling support tools is important to assess how changes in the results are attributed to these uncertainties.

Modeling efforts have explored the dynamics and feedbacks of food-water systems using hydro-economic modeling approaches (Harou et al. 2009), factoring the particular characteristics of water and agricultural production systems. Various studies have used modular and response functions coupling taxonomies to represent the coevolution of agricultural production systems with surface water systems (Giuliani et al. 2016; Forni et al. 2016; Maneta et al. 2020) and groundwater systems (Graveline 2019; Afshar et al. 2020; MacEwan et al. 2017), to assess impacts of exogenous changes and water policies.

As HEMs grow in their complexity, improved diagnostic tools to better map how inputs and calibration uncertainties shape the outputs become increasingly important. Sensitivity Analysis (SA) is a formalized methodology to study how the uncertainty in the output of a model is attributed to uncertainties in the model inputs (Saltelli 2002). Two general SA methods are used depending on the taxonomy of the model: local and global sensitivity analysis. Global sensitivity analysis is used for non-additive models where there are nonlinear interactions among inputs. The objective of this analysis is to quantify the variability of model outputs that result from direct and higher order effects (interactive effects) of uncertain inputs. Additionally, GSA considers the variation of all the uncertain inputs at the same time, whereas local SA is performed by varying one input at a time.

SA is widely employed in environmental and hydrologic modeling (Pianosi 2016; Song et al. 2015), to explore inputs prioritization (Hashemi and Mahjouri 2022; Budamala and Baburao Mahindrakar 2020; Karimi et al. 2022), climate change uncertainties (Fayaz et al. 2020), and calibration performance (El Harraki et al. 2021). Despite the large use of HEMs in food-water systems, diagnostic sensitivity analysis is seldom performed and is often limited to exploring impacts on the outputs from a single input through scenario analysis without exploring all the uncertain space of inputs with some exceptions (D’Agostino et al. 2014; Singh 2022; Ghadimi and Ketabchi 2019). Furthermore, sensitivity analysis has also been applied to calibrated agricultural production models, where the diagnostic results were used to identify how changes in economic variables (Shirzadi Laskookalayeh et al. 2022; Arribas et al. 2017) and calibration parameters (Graveline and Merel 2014) shape revenues and inputs allocation forecasts.

In this work, we contribute a coupled HEM and a GSA diagnostic framework for an improved understanding of the most consequential factors that shape the evolution of the food-water system in California’s San Joaquin Valley (SJV), and provide insight for assessing a groundwater pumping restriction policy. The HEM used in this study uses a PMP model to emulate agricultural production, coupled with a groundwater response function (GRF), which was embedded in the PMP model through an ANN. Our diagnostic GSA explores uncertainties in economic, crop production, groundwater restriction and calibration factors. Additionally, we perform the diagnostic for two baseline conditions, to show how the selection of the baseline changes the results of the GSA and groundwater restriction impacts. This framework is applied for the Wheeler Ridge-Maricopa Water Storage District, a water district representative of the SJV.

This paper is organized as follows. In Sect. 2, we describe the study area and the agricultural and water characteristics of the water storage district. In Sect. 3, we lay out the coupled hydro-economic modeling framework used in this paper, including a description of the calibration process and the GSA experiment. Results are summarized in Sect. 4, where we analyze the diagnostic insights from the GSA to clarify key factors shaping the performance metrics of the model. Finally, conclusions and areas for future research are described in Sect. 5.

2 Study Area Description

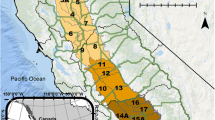
The Wheeler Ridge-Maricopa Water Storage District (Fig. 1) is the third-largest district in crop acreage in Kern County, one of the most productive counties in the United States (USDA 2019). Perennial crops are the commodities mainly produced in the district, including vines, subtropical fruit trees and nut trees. Perennials cropland has increased overtime as shown in Fig. S2 of the Supplemental Information (SI). In the SJV, highly variable surface water supplies have significant impacts on aquifers as groundwater pumping for irrigation serves as an important backstop source of water during dry periods (Lund et al. 2018), affecting groundwater storage (Xiao et al. 2017; Yin et al. 2021) and groundwater depths (Vasco et al. 2019). With climate change, stress on groundwater is expected to exacerbate as changes in precipitation, temperature and snow-pack have impacts on surface water supply (Fernandez-Bou et al. 2021). Water stakeholders located on overdrafted groundwater basins are facing regulatory pressure to achieve groundwater sustainability following the objectives of the Sustainable Groundwater Management Act (SGMA) (DWR 2021). Recent studies highlight the implementation of groundwater and land use controls on agriculture to achieve sustainability (Hanak et al. 2019), such as pumping restrictions (Miro and Famiglietti 2019; MacEwan et al. 2017), pumping fees (Stone et al. 2022) and land fallowing (Li et al. 2018; Bryant et al. 2020; Van Schmidt et al. 2022). In this study, we assess a candidate groundwater pumping restriction while considering other uncertainties.

Fig. 1
figure 1

Wheeler Ridge-Maricopa Water Storage District located in the San Joaquin Valley, California. The district spans two groundwater basins: Kern County and White Wolf

Full size image

3 Methodological framework

The coupled HEM approach used in this paper integrates a groundwater depth response function, modeled using an ANN, in a calibrated agricultural production model. Both models were calibrated separately and coupled as explained in the following subsections.

3.1 Agricultural production model

We modeled the agricultural production system following PMP (Howitt et al. 2012) using two baselines: the average of 2010-2012 (wet period) and the average of 2013-2015 (dry period). The average of these years was taken from observed data used in the calibration process. By using a time window average, we capture the average farmers behaviour during each water condition. The calibration process can be found in the SI.

The calibrated model (Eqs. 1 to 6) maximizes the economic revenue at the water district level by optimizing the input allocation (\(x_{i,j}\)) of j={water, land, labor, other supplies} for production of crop i={almonds and pistachios, alfalfa, cotton, cucurbits, other deciduous, other truck, grain, other field, fresh tomatoes, processing tomatoes, onions and garlic, sugar beets, dry beans, pasture, subtropical, vine, potatoes, safflower, corn} and use of water (\(wat_{w}\)) by source w = {surface water, groundwater}. The second term in the objective function (Eq. 1) is the crop specific exponential cost function, where the calibration parameters \(\gamma _{i}\) and \(\delta _{i}\) are parameterized using dual values (\(\bar{\lambda }_{land,i}\)) obtained from solving the linear model in the SI (Eqs. S1-S4). \(\delta _{i}\) equals \((\omega _{i,land} + \bar{\lambda }_{land,i}) / (\gamma _{i} \exp (\gamma \bar{x}_{land,i}))\) where \(\gamma _{i}\) equals 1/\(\theta _{i} \bar{x}_{i}\), \(\bar{x}_{land,i}\) is the baseline land use and \(\theta _{i}\) is the own-price supply elasticity.

$$\begin{aligned} \begin{aligned} Max_{x_{i,j},wat_{w}}\prod&= \sum _{i} (p_{i} yld_{i} y_{i}) - \sum _{i}(\delta _{i} \exp (\gamma _{i} x_{i,land}))- \\&\sum _{i}\sum _{j\ne land, water}(\omega _{i,j} x_{i,j})-\sum _{w}(\hat{\omega }_{w} wat_{w}) \end{aligned} \end{aligned}$$
(1)

where \(p_{i}\) is the price by crop (\(\$/ton\)), and \(yld_{i}\) is the crop yield change coefficient. In the third term there is a linear cost of the use of inputs j, where \(\omega _{i,j}\) is the marginal cost of each input per acre. Lastly \(\widehat{\omega }_{w}\) is the cost per acre foot of water used from every source. The pumping cost (\(\widehat{\omega }_{GW}\)) is a function of depth and electricity price described in the SI. \(y_{i}\) is the total production (tons) by crop given by a Constant Elasticity of Substitution (CES) production function with constant returns to scale (Debertin 2012), defined as:

$$\begin{aligned} y_{i}=\tau _{i} [\sum _{j}\beta _{i,j} x^{\rho _i}_{i,j}]^{1/\rho _i} \end{aligned}$$
(2)

where \(\tau _{i}\) is a scale parameter given by \(\bar{y}_{i} \bar{x}_{i}/[\sum _{j}\beta _{i,j} x^{\rho _i}_{i,j}]^{1/\rho _i}\), where \(\bar{y}_{i}\) is the baseline crop yield. The parameter \(\beta _{i,j}\) represents the relative use of each input. The parameter \(\rho\) is equal to (\(\sigma\)-1)/\(\sigma\) where \(\sigma\), elasticity of substitution, is 0.17 for all crops.

The optimization model has a set of resource constraints: land availability (Eq. 3), surface water availability (Eq. 5), and groundwater pumping restriction (Eq. 6). Where \(b_{land}\) is the available land, \(b_{SW}\) is the available surface water and \(b_{GW}\) is the groundwater pumping capacity. GWR represents the groundwater pumping restriction policy.

$$\begin{aligned} \sum _{i} x_{i,land} \le b_{land} \end{aligned}$$
(3)
$$\begin{aligned} \sum _{i} x_{i,water} \le \sum _{w}wat_{w} \end{aligned}$$
(4)
$$\begin{aligned} wat_{SW} \le b_{SW} \end{aligned}$$
(5)
$$\begin{aligned} wat_{GW} \le (1-GWR) b_{GW} \end{aligned}$$
(6)

3.2 Groundwater Depth Change Response

In order to estimate the groundwater depth (GWD) change response from agricultural pumping, an ANN was calibrated. The groundwater depth change (\(\Delta d_{g,t}\)) at each year (t) of simulation is modeled at a water district level. The ANN was calibrated using data from twenty-four water districts within the Kern county region listed in Table S1, and using a categorical variable to forecast district-specific changes (g). The ANN has nine input variables, one output variable, and two hidden layers, each with nine neurons, as shown in Fig. 2. The variables used from the year of the simulation t and the previous year t-1 are: San Joaquin Valley Water Year Hydrologic Classification Index (WYI), total volume of surface water used for irrigation (VSW), total volume of groundwater used for irrigation at the end of the irrigation season (VGW), and volume of intentional groundwater recharge (VIR). Data sources for the calibration process are explained in Sect. 3.4. Details about the ANN calibration and validation results for Wheeler Ridge-Maricopa can be found in the SI.

Fig. 2
figure 2

Artificial Neural Network (ANN) graphic representation which estimates the change in the average groundwater depth (\(\Delta d_{g,t}\)) by water district

Full size image

3.3 Global Sensitivity Analysis

The economic production model and groundwater depth response neural network were calibrated and coupled in a single model in Python. The selected model input variables analysed in the GSA are: crop prices, crop yield change coefficients, surface water price, price of electricity and crops own-price supply elasticities. Additionally, a potential groundwater restriction was included. Three outputs were analyzed in the diagnostic: groundwater depth change, total land use and total net revenue. Figure 3 shows the flow of inputs for the calibration of the model and simulation.

Fig. 3
figure 3

Global Sensitivity Analysis experiment. In red are the inputs selected for the GSA experiment from all the inputs used (green boxes). The gray arrows represent the flow of inputs for the calibration of the PMP model. The flow of inputs (in red) and outputs for the GSA experiment is depicted with black arrows. The yellow boxes represent the two models (PMP and ANN) and the red boxes represent the outputs of analysis. \(P_{i} = \sum _{i,j} (p_{i} y_{i} - \omega _{i,j} x_{i,j}) x_{land,i}\)

Full size image

A variance-based GSA method, Sobol, was used for this study (Sobol’ 2001). It uses the principle of variance decomposition to estimate the single interaction, higher order, and total effects of each input variable on the output. This method is computationally efficient, easy to interpret, and mathematically reliable.

Following Saltelli et al. (2010), the first order sensitivity index (S1) represents the contribution of a parameter \(X_i\) to the variance of the output Y given by Eq. 7. V(Y) is the total variance of the output and \(X_{\sim i}\) is a matrix of all parameters but \(X_{i}\). The mean of Y is taken over all the possible values of \(X_{\sim i}\) while keeping \(X_{i}\) constant. \(S1_{i}\) is normalized so the first order indices have values between zero and V(Y).

$$\begin{aligned} S1_{i} = \frac{V_{X_i}(E_{X_{\sim i}}(Y\vert X_{i}))}{V(Y)} \end{aligned}$$
(7)

Using variance decomposition, Sobol indices capture interactions among parameters that are present due to nonlinearities in the model. The second order sensitivity (S2) is given by the joint effect of two parameters \((X_{i},X_{j})\) on the variance of the output Y. This index is the result of the difference between the joint effect of the two parameters minus their first order effects as described by Eq. 8.

$$\begin{aligned} S2_{ij} = V(E_{X_{\sim ij}}(Y\vert X_{i},X_{j})) - V(E_{X_{\sim i}}(Y\vert X_{i})) - V(E_{X_{\sim j}}(Y\vert X_{j})) \end{aligned}$$
(8)

Finally the total order index (ST) for an input \(X_i\) is given by Eq. 9. This represents the total effect of any input parameter \(X_{i}\) on the output Y, accounting for the first order effect and higher order effects. Where \(V_{X_{\sim i}}(E_{X_{ i}}(Y \vert X_{\sim i}))\) is the first order effect of \(X_{\sim i}\). V(Y) minus \(V_{X_{\sim i}}(E_{X_{ i}}(Y \vert X_{\sim i}))\) is the total contribution of \(X_i\) to the variance of the output Y.

$$\begin{aligned} ST_{i} = 1 - \frac{V_{X_{\sim i}}(E_{X_{ i}}(Y \vert X_{\sim i}))}{V(Y)} \end{aligned}$$
(9)

Since the distribution of the selected input variables is unknown we used the Saltelli sampling scheme (Saltelli 2002), using minimum and maximum boundaries for each input (Table 1). For uncertainty on crop prices, we assume a relative price uncertainty of 20% and changes in yields of plus and minus 10% from the baseline as assessed by Medellín-Azuara et al. (2011) and Pathak et al. (2018). Crop prices show constant volatility as they are subject to global markets, while yield changes can be the result of farm-scale decisions (e.g. water stress, technology and fertilization) and climate factors. We used the baseline surface water price plus and minus 20% boundaries. For the price of electricity we used the minimum and maximum values reported in the analysis period. For own-price supply elasticities we used the minimum and maximum values found in the literature (Maneta et al. 2020; Russo et al. 2008; Volpe et al. 2010), or plus and minus 20% from the estimated values. Finally, we included a groundwater pumping restriction policy, which can restrict up to 50% from the baseline groundwater pumped for each year. Values used for the GSA experiment are reported in Tables S2-S4 of the SI.

Table 1 Boundaries of input variables for Global Sensitivity Analysis Experiment
Full size table

To perform this experiment we used the Python library SALib (Herman and Usher 2017). The number of simulations to achieve significance and convergence on the sensitivity indices depend on the number of samples and number inputs (Saltelli et al. 2010). We performed simulations using 1,000 to 20,000 samples (n) for each input. The convergence of ST indices happened after n=2,000, however S1 indices converged after n=15,000. For the final simulations we chose n=20,000 samples for each input for a total of 2,080,000 state of the world simulations for the wet year conditions and 1,960,000 for the dry year conditions.

3.4 Data Sources

Land use data is available from KCDAMS (2021). Crop water requirements were obtained from the California Department of Water Resources (DWR) (DWR 2020a). Price and yield information was obtained at the county-level data for Kern (USDA 2019). We assumed subsidies for crops that exhibit potentially negative marginal profitability under historical conditions. Costs of production were obtained from UC Davis Cost and Return Study estimates, using proxy crop costs per crop category (UC Davis 2015). Agricultural surface water cost was estimated from rates published in the water district Agricultural Water Management Plans (DWR 2020b). Surface water delivery, groundwater pumping and groundwater recharge amounts were obtained from simulations of the California Food-Energy-Water Systems (CALFEWS) model (Zeff et al. 2021). Groundwater depths and pumping rates used for the ANN calibration were obtained from C2VSim-FG outputs (Brush and Dogrul 2013) using the weighted-averaged groundwater depth to agricultural pumping. Water year classification was obtained from DWR (2020c). Additionally, the electricity costs, used in the pumping cost function, were obtained for agricultural customers reported by PG &E (2021).

4 Results and Discussion

Results allow us to compare the sensitivity of groundwater depth change, total net revenue and total land use to input variable uncertainties. Figures 4 and 5 show the Sobol indices for wet year and dry year conditions, respectively. Second order indices are depicted by the ribbons of the chord-diagram. First order indices are the next outer circle, and total order indices are depicted in the outermost color circle. Variables related to the water supply (surface water price, price of electricity and groundwater restriction) are labeled as “water”. Visualizations of the results were filtered to show the ten inputs with the highest ST for each output. The Python library used for the experiment, SALib, computes confidence intervals for the three indices, which satisfied a significance level of 0.05 for all the results. First order effects (S1) from Sobol were compared to Delta Moment-Independent Measure indices which can be found in the SI (Tables S5-S10).

For wet year conditions (Fig. 4), the results show that highest ranked input variables are the groundwater restriction and variables related to the most produced crops: vine, almonds and pistachios, other truck and subtropical. Allocation of land is highly sensitive to a restriction of groundwater pumping, which has a 68.3% ST. Additionally, the price of almonds and pistachios, price of other truck, and yield of cotton are among the most important inputs that affect land allocation based on their ST. Total net revenue is highly sensitive to price and yield of vine, the most produced crop in the district, and price of other truck crops.

For the wet year baseline 74% of irrigation was supplied from surface water, which price has a 13% ST to the groundwater depth change. Additionally, joint effects for GWD change are significant between price of almonds and pistachios with groundwater restriction (2.6% S2), which is also the largest joint effect of the study, and between the yield and price of almonds and pistachios. Groundwater pumping restriction has the largest ST to GWD change of 73.08%.

Fig. 4
figure 4

Results GSA for wet year conditions for Total Land Use (A), Total Net Revenue (B), and Groundwater Depth Change (C). SE=Supply Elasticity

Full size image

As shown by the singular and joint effects, profitability changes due to crop price, yield and surface water price variation, have large impacts on land use and water use. This translates to changes in groundwater depth. The supply elasticity of almonds and pistachios used in the PMP calibration process has a total effect of 4% on total land use and 7.6% on groundwater depth change, showing the highest sensitivity indices from these calibration parameters in the analysis.

Results for the dry year are shown in Fig. 5. Compared to the wet year, a lower number of inputs have large ST. Given a higher dependence on groundwater pumping (68.4% of the baseline water demand), crop production is less flexible and more sensitive to water shortages. Expansion of perennial tree crops has been driven by increasing profits. However, these crops have a large water demand, 4 acre-feet per acre on average, making the food system vulnerable to water shortages. Groundwater restriction is the variable with the largest first order and total order effects on the total land allocation and groundwater depth change, with 90% ST.

Fig. 5
figure 5

Results GSA for dry year conditions for Total Land Use (A), Total Net Revenue (B), and Groundwater Depth Change (C). * = Price, PT = Processing tomatoes, SE = Supply Elasticity, Al. &Pis. = Almonds and Pistachios

Full size image

Total land use is sensitive to price of other truck crops with 7.0% ST. Total net revenue as in the wet year is highly sensitive to price and yield of vine. The groundwater depth changes is highly sensitive to yield and price of subtropical crops with ST of 20% and 15% respectively, which are highly contributed from the high joint effect between these two inputs (2.7% S2), and the joint effect between subtropical crop yield and the groundwater restriction (2.5% S2).

By comparing wet and dry year conditions, we can observe that during a dry year S1 and ST effects of variables related to the most important crop groups are the most significant along with a groundwater restriction. This highlights the importance of groundwater, and that with a groundwater restriction the allocation of total land would likely be substantially reduced. S1 effects for the dry year are closer to representing the total variance of the outputs than in the wet year, meaning that direct effects are largely shaping the performance of the system. Additionally, during a wet year, multiple single and join effects are affecting the outputs of analysis, given the adaptation of farmers modeled by PMP in a year with more flexible water supply. In both years the price of electricity resulted in low indices, given the low electricity tariffs for agricultural users.

Other objectives beyond factor ranking can be achieved using the results of the diagnostic GSA. Factor fixing is a common practice that can reduce the uncertainty in the forecasts. Inputs with ST \(\simeq 0\) can be fixed at any value in the space of the variation boundaries and will not affect the outputs. Since we are focusing on three outputs of the model and two base conditions, we have six total order indices for each input. Even though there are no inputs that satisfy this condition for all the outputs, some inputs show consistently low total order sensitivity, for example the supply elasticity of other deciduous and corn, yield of fresh tomatoes, and price of alfalfa and grain; suggesting that changes of these outputs would not have any significant effect to the outputs and can be fixed. In PMP modeling, crop own-price supply elasticities is one of the most uncertain inputs due to the limited information about them in the context of the SJV. Our analysis suggests that these parameters are candidates for factor fixing given their low ST.

Results from the diagnostic GSA can be used to explore the uncertainty space of the outputs, which can support stakeholders to identify areas of interest in the output space and trade-offs. Figure 6 shows the performance of the outputs at different percentage levels of groundwater pumping restrictions (color gradient). Trade-offs among outputs are depicted by the lines in the parallel-coordinate plot, each one represents the results from a state of the world simulated in the GSA experiment.

Fig. 6
figure 6

Random sample of five hundred scenarios for wet year and dry year from the diagnostic sensitivity analysis experiment

Full size image

Our results show that the same level of pumping restriction can have different outcomes. For example, scenarios with a 50% pumping restriction in both water conditions can result in different levels of total land use and depth change. This is driven by the profitability of crops with high ST and high joint effects with the restriction policy, such as price and yield of almonds and pistachios, price and yield of subtropical crops and surface water price. The diagnostic GSA results show the dominant inputs and joint effects that explain the nuances in the trade-offs. Furthermore, the pumping restriction does not have a clear effect on the net revenue for which other inputs with higher ST have a greater impact. Stakeholders can use these results to identify specific scenarios supported by the diagnostic GSA results and understand the drivers of particular results. Additionally, these results can inform policy makers about the expected magnitude of change in policy performance and the largest vulnerabilities in the system.

5 Conclusions

GSA diagnostic results inform how much each input and their joint effects impact three outputs of interest: total land use, total net revenue, and groundwater depth change. The diagnostic provides insight about dominant inputs (with high ST) or inputs (with ST \(\simeq\) 0) that can be fixed. The inclusion of a groundwater restriction policy allowed us to explore its impacts on the food-water system and how other dominant inputs can affect its performance. Even though the restriction parameter showed the largest sensitivity indices, other inputs also showed substantial total order effects. Changes in prices and yields of tree crops and vines can be considered vulnerabilities of the system and affect policy results and trade-offs among system performance metrics. Diagnostic results can be used to inform stakeholders about potential drivers of undesirable results, vulnerabilities and other elements to consider for the development of a robust policy. Future work will include other groundwater management policies such as a groundwater pumping fee and land restrictions.

Our findings show that significant differences in the diagnostic results emerge from two baseline water condition scenarios. We suggest that the use of the diagnostic framework shown in this study is applicable for any HEM. Furthermore, performing this diagnostic under different baselines is particularly important for studies of places with highly variable water supplies such as the San Joaquin Valley, and other places in Mediterranean, arid, and semi-arid climate regions.