Towards a More Robust Evaluation of Climate Model and Hydrological Impact Uncertainties

Abstract

The uncertainty of climate model projections is recognized as being large. This represents a challenge for decision makers as the simulation spread of a climate model ensemble can be large, and there might even be disagreement on the direction of the climate change signal among the members of the ensemble. This study quantifies changes in the hydrological projection uncertainty due to different approaches used to select a climate model ensemble. The study assesses 16 Euro-CORDEX Regional Climate Models (RCMs) that drive three different conceptualizations of the MIKE-SHE hydrological model for the Ahlergaarde catchment in western Denmark. The skills of the raw and bias-corrected RCMs to simulate historical precipitation are evaluated using sets of nine, six, and three metrics assessing means and extremes in a series of steps, and results in reduction of projection uncertainties. After each step, the overall lowest-performing model is removed from the ensemble and the standard deviation is estimated, only considering the members of the new ensemble. This is performed for nine steps. The uncertainty of raw RCM outputs is reduced the most for river discharge (5 th , 50 th and 95 th percentiles) when using the set of three metrics, which only assess precipitation means and one ‘moderate’ extreme metrics. In contrast, the uncertainty of bias-corrected RCMs is reduced the most when using all nine metrics, which evaluate means, ‘moderate’ extremes and high extremes. Similar results are obtained for groundwater head (GWH). For the last step of the method, the initial standard deviation of the raw outputs decreases up to 38% for GWH and 37% for river discharge. The corresponding decreases when evaluating the bias-corrected outputs are 63% and 42%. For the bias corrected outputs, the approach proposed here reduces the projected hydrological uncertainty and provides a stronger change signal for most of the months. This analysis provides an insight on how different approaches used to select a climate model ensemble affect the uncertainty of the hydrological projections and, in this case, reduce the uncertainty of the future projections.

Introduction

The impact of climate change on the water sector in terms of duration and magnitude of floods and droughts has been significant, and it is expected that the impacts will accelerate during the coming decades (Cisneros et al. 2014; Winter et al. 2020). The assessment of climate change impacts on water resources has attracted substantial research interest in the last decades, focusing on uncertainty assessments towards improving decision-making (e.g. Meresa and Zhang 2021; Gaur et al. 2021). Assessing the impacts involve raw or bias-corrected outputs of an ensemble of General Circulation Models (GCMs) or Regional Climate Models (RCMs) as input to (a) calibrated hydrological model(s). Using this approach, the projected changes and statistics of different hydrologic variables can be estimated.

The recognised uncertainties in climate change projections result in uncertainties on projected hydrological impacts that are so large that, in practice, they restrain climate change adaptation (Kundzewicz and Stakhiv 2010; De Niel et al. 2019), particularly with respect to precipitation (Collins 2017). The dominating uncertainty most often originates from climate models (Refsgaard et al. 2016). This uncertainty can basically be reduced by improving climate models, which is a long-lasting and continuous effort (e.g., Flato et al. 2013; Di Luca et al. 2015). In the meantime, it is relevant to evaluate how realistic the uncertainties of currently used climate model projections are and to assess whether they are overestimated (or underestimated).

The skill of the GCMs and RCMs in simulating the observed climate varies with region and variable because of the different theories, formulations and parameterisations behind each model (e.g., Rummukainen 2016; Jury et al. 2015). As a result, members of a climate model ensemble could provide unrealistic projections for specific regions, variables and/or metrics, which are likely to increase the ensemble spread and the uncertainty of the projection.

Given their different simulation skills, it seems plausible that assigning low weights to less trustworthy models could reduce the uncertainty of the projection. However, it should be noted that if the group of best performing (behavioural) climate models happens to have the largest spread in climate signal, a weighting may instead lead to increased projection uncertainty.

In practice, two approaches are used for weighting climate models. The first approach assumes that the different climate model projections have the same probability of being true, usually referred to as model democracy (Knutti 2010; Farjad et al. 2019). The second approach evaluates the simulation skills of the climate models for a historical period, and/or additional criteria, to assign a weight to each model and produce a weighted projection (e.g., Christensen et al. 2010; Evans et al. 2013; Pennell and Reichler 2011; Wang et al. 2019; Lehner et al. 2019; Raju and Kumar 2020). The climate modelling community mostly uses model democracy whereas assigning weights is mostly used by the impact community (Chen et al. 2017). Alternatively, models with poor simulation skill can be removed from the ensemble.

Two main approaches deal with uncertainty. The goal of the first approach is to preserve the projection spread of the complete model ensemble while reducing the number of models included in the ensemble (e.g. Evans et al. 2013; Lee and Kim 2017; Seo et al. 2018; Pechlivanidis et al. 2018; Farjad et al. 2019). Models that resemble the projection of other models are removed resulting in a reduction of the, often heavy, computational burden when analysing a combination of several emission scenarios, climate model projections and impact models. The second approach intends to reduce the number of models used in the ensemble by removing or weighting the models in the ensemble based on specific criteria (Wang et al. 2019). This approach is based on the hypothesis that the uncertainty of the projection is often overestimated because of the variable performance of climate models, and that the robustness of the projection increases if only the better performing models are used. Few studies have analysed the latter approach for impact studies. For instance, Lehner et al. (2019) reduced the initial runoff projection uncertainty by 57% in catchments in the US when the models were observationally constrained. Similarly, Wang et al. (2019) used streamflow-based metrics to assign weights to climate models concluding that using bias-corrected models and equal weighting of the climate models seemed enough to decrease uncertainty in impact assessments.

Different methodologies have been used to estimate the uncertainty of a climate change impact projection. These vary from a simple evaluation of the range of the projections (Her et al. 2019) to more complex analysis, such as estimation of d-factors (Najafzadeh et al. 2021) or Bayesian model averaging (Najafi and Moradkhani 2015). Nevertheless, the final objective of any of these approaches is to provide an estimation of the uncertainty of the projection.

The aims of this study are i) to introduce a new methodology for reducing the climate model ensemble based on simulation skills in the present climate, and ii) to evaluate how the integration of climate model simulation skills to climate model selection affects the uncertainty of the future projections of river discharge and groundwater head. Our underlying assumption is that climate models with large biases in the present climate are likely to provide the least reliable projections of future climate (Knutti 2008). The results of this new approach are compared to results from other methods to demonstrate it’s potential. This approach has the potential of being an important contribution for the improvement of the decision-making process.

Methodology

Study Area

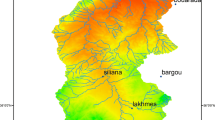
The study is carried out in the Ahlergaarde catchment (1,055 km²), located in western Denmark (Fig. 1). The land surface elevation ranges from 150 m above sea level in the east to 25 m above sea level at the outlet of the catchment in the west (Sebok et al. 2016). The annual mean precipitation is 1,050 mm with an annual mean temperature of 8.2 degrees Celsius. The shallow aquifer mostly consists of sandy and silty deposits (Houmark-Nielsen 1989). Intensive agriculture is the dominating land use (80%), followed by forests (10%), heath (6%) and urban areas (4%) (Ridler et al. 2014).

Fig. 1

Location of the Ahlergaarde catchment along with the observation stations used for evaluation of the model

Climate Models

16 GCM-RCM combinations (Table S1) from the EURO-CORDEX initiative (Jacob et al. 2014) are used. Each GCM is driven by Representative Concentration Pathway (RCP) 8.5 and downscaled to a spatial resolution of 0.11°.

The RCM outputs are remapped to match the observed temperature (20 km × 20 km) and precipitation (10 km × 10 km) grids produced by the Danish Meteorological Institute. Raw climate model outputs usually have systematic errors when compared to the observations (Maraun 2016). Therefore, the RCM outputs are bias-corrected employing a Distribution Based Scaling method (Seaby et al. 2013) which uses a double Gamma distribution to correct precipitation and a normal distribution to correct temperature. For precipitation, the cut-off threshold between the two distributions is set at the observed 90th percentile. In an initial step, the number of observed and simulated days without precipitation are matched by setting a threshold below which the daily precipitation outputs are set to zero (Pastén-Zapata et al. 2019).

Hydrological Model Setup, Calibration and Validation

The MIKE SHE code, a physically-based, integrated and fully distributed model (Abbott et al. 1986; Graham and Butts 2005) is setup for the catchment with a spatial resolution of 500 m × 500 m. The MIKE SHE code is the basis of the national hydrological model of Denmark (Henriksen et al. 2003; Højberg et al. 2013; Stisen et al. 2019) where the saturated zone, the unsaturated zone, river flow, evapotranspiration and overland flow are included. The dynamics of the unsaturated zone are of critical importance for the hydrological response of climate change.

The robustness of the results is assessed using three different model conceptualizations to simulate flow and evapotranspiration in the unsaturated zone: Richards’ equation, gravity flow and two-layer water balance. The models are described in supplementary Sect. S3 and their calibration and validation procedure and results are shown in Sect. S3.1.

Each bias-corrected GCM-RCM combination (16 in total) is used as the driving climate for each of the calibrated hydrological models (3 in total), producing 48 simulations in total. The average results of each climate model, across the three hydrological models, are used to estimate the projected absolute changes in discharge and groundwater head.

Climate Model Evaluation Metrics and Ranking

The simulation skill of the climate models is determined by comparing observations to simulations of precipitation from 1991 to 2010 following two different pathways (Fig. 2). The primary difference between pathways A and B is that in A, ranking is based on the match of the raw CMs to observed precipitation while in B, ranking is determined by the match of the bias-corrected CM output to observed precipitation following a five-fold cross-validation approach.

Fig. 2

Diagram of the process used to evaluate the change in uncertainty of the hydrological projections, CM: Climate Model

The cross-validation scheme evaluates whether the bias-correction method provides accurate results outside its training period (Gutiérrez et al. 2019). The five-fold cross validation method divides the observation period into five equal-length and non-overlapping blocks, where four of the blocks are used to train the parameters which are then used to correct the remaining block. This is repeated for all blocks until a cross-validated time series of the same length of the period with observations is produced.

It has been suggested that evaluating cross-validated outputs from free-running bias-corrected models (as pathway B) could give misleading results (Maraun and Widmann 2018). Nevertheless, these outputs are typically used to assess the impacts of climate change and cross-validation is employed to evaluate the reliability of the bias-correction method (Maraun 2016).

A set of nine metrics (9 m) is defined to evaluate the climate models with respect to precipitation (see Table S2). The metrics assess the simulation skills for the mean, ‘moderate’ extremes, ‘highly’ extremes and variability of precipitation. The extreme metrics are taken from the daily extreme climate change indices (Zhang et al. 2011). To explore the importance of the selection of the metrics, subsets of six (6 m), and three metrics (3 m) are also included in the analysis. In 3 m, the mean behaviour and one ‘moderate’ extreme metrics are evaluated, whereas 6 m includes more metrics on ‘moderate’ extremes and 9 m adds three ‘highly’ extreme event metrics.

For each metric, the climate models are assigned a score between 1 (smallest bias) and 16 (largest bias). For the purpose of ranking, the scores of all metrics for each model are summed up. Based on the final sum, models are ranked to differentiate their overall relative simulation skills. A low relative value of the final sum represents a model with good simulation skill whereas a high relative value indicates poor simulation skill.

Analysis of the Uncertainty in the Projection

The uncertainty of the hydrological projections is evaluated by analysing the projected ensemble mean river discharge and mean groundwater head of the 16 ensemble members by the end of the century (2071–2100). The analysis focuses on the 5th, 50th and 95th percentiles of each variable from the best performing RCMs still remaining at a given step in the analysis.

The change in the uncertainty is analysed in a series of steps (see Fig. 2). For each step, a set of phases are followed, as described next for step ‘n’:

• Phase 1. Estimate the standard deviation of the variable of interest (river discharge or groundwater head) considering the RCMs in the ensemble at the beginning of step ‘n’.

• Phase 2. For all the RCMs in the current ensemble, evaluate their ability to simulate the historical precipitation using the different subsets of metrics (Table S2) and rank them, as described in Sect. 2.4.

• Phase 3. Remove the worst-ranked RCMs from the ensemble.

• After reaching Phase 3, all three phases are repeated for the following step ‘n + 1’. This approach is used for nine steps, leaving seven models in the final ensemble. Previous analyses (e.g., Evans et al. 2013; Pennell and Reichler 2011) indicate that the order of seven models is considered as an appropriate ensemble size.

Comparison with Other Weighting Methods

The results of this approach are compared to other weighting methods. The reliability ensemble averaging (REA) and the upgraded reliability ensemble averaging (UREA) methods are selected for comparison because these methods can assign weights with larger differences to the climate models (Wang et al. 2019; Chen et al. 2017). Both are multiple criteria methods and can reduce the discharge uncertainty in the historical period to a larger extent than other weighting methods (Wang et al. 2019). In the present study, only the projections of precipitation are evaluated to define the climate model weights of these methods. REA assigns the weight of a model by assessing its reliability, which consists of the product of two components: its biases in the historical period and the convergence of its projection with the projection of the whole model ensemble (Giorgi and Mearns 2002). UREA removes the criteria of convergence and replaces it with the skill of each individual model to simulate the observed interannual precipitation variability (equations used are shown in the supplementary Sects. S4 and S5).

Uncertainty Assessment for the Different Methods

The uncertainty of the methods is assessed initially using the standard deviation of the projection by the end of the century and subsequently the signal to noise ratio (SNR) of the projected change. The standard deviation of the ensemble is estimated using the square root of the sum of the squared differences between the projection of model i (X_i) and the projected mean of the ensemble (µ), multiplied by the weight (W) of model i:

$$\sigma =\sqrt{{\sum}_{i=1}^{N}{W}_{i}\cdot {\left({X}_{i}-\mu \right)}^{2}}$$

(1)

The SNR estimates the uncertainty of the projected change from the reference period (1981 to 2010), to the future period (2071 to 2100). Thus, the SNR is estimated by dividing the projected mean change of the model ensemble (µ) by its standard deviation (σ):

$$SNR=\frac{\mu }{\sigma }$$

(2)

A larger SNR indicates that the uncertainty is relatively small, compared to the larger uncertainty of smaller SNR values.

Results

Calibration and Validation of the Hydrological Model

The skill of all models to simulate discharge is good with the gravity flow model slightly underperforming (Table S3). Simulation of groundwater head using Richards’ equation is worse compared to the other models, but it is the best model to match observed soil water content. In summary, there is a significant variability in the simulation skill of the different hydrological models for the different variables and evaluated statistics. However, for most metrics the two-layer model provides the best match to the observed values, given the variability in performance for the different variables, it can be inferred that the models included in the ensemble complement each other. A complete assessment of the results and decription of the calibration and validation procedure is available in the supplementary material (Sect. S3).

Change in the Uncertainty of the Projection

Both the raw and bias-corrected GCM/RCM combinations are ranked based on their simulation skill for each of the evaluation metrics (Table S2). The ranking is used to discard the model with the poorest performance during each step. The resulting change in the uncertainty of the hydrological ensemble after each step is shown in the following sections. The results represent the mean of the results of the three hydrological model configurations. Note that the bias-corrected precipitation projections are used as input to the hydrological models for both pathways A and B because this is a standard practice in impact assessments. The final ensemble of climate models, after the ninth step, for both pathways is shown in Table S1. Note that for pathway A there are six models in the final ensemble because two models had the same score at the ninth step. For pathway B, seven models are left in the final climate model ensemble.

Groundwater Head

The projected mean groundwater head under pathway A changes only slightly after each step for the evaluated percentiles and all the subsets of metrics (Fig. 3, first column). The standard deviation increases (negative decrease in standard deviation) for all steps when using the full set of metrics (9 m), showing no clear relation between the historical performance of climate models and hydrological projections. When the most extreme metrics are removed and only the moderate extreme and the mean metrics remain (6 m), a decrease in uncertainty is found after deletion step 5. If only the metrics for the mean response and one extreme metric are left (3 m), a decrease in uncertainty is observed in earlier steps. The standard deviation is reduced the most for 6 m: 32% for the 95th percentile, 31% for 50th percentile, and 36% for the 5th percentile.

Fig. 3

Change in the projected mean (dashed lines) and standard deviation (solid lines) of the 5th, 50th and 95th percentiles of the groundwater head (in meters). The decrease in uncertainty is shown as change in the standard deviation of the ensemble after each step, compared to the standard deviation of the initial ensemble. Results are shown for pathway A (left column) and pathway B (right column) and for the subsets of metrics (different symbols) analysed. The grey area represents the spread (maximum – minimum) of the projection for each step. The spread is shown for the set of metrics that reduced the initial uncertainty the most: 6 m for pathway A and 9 m for pathway B

The mean of the projections of pathway B does not vary much after each step, independently of the subset of metrics and the percentiles that are analysed (Fig. 3, second column). The uncertainty is reduced after each step for all the subsets of metrics. The subset that includes all the metrics (9 m) produces the largest decrease in the initial standard deviation., A significant decrease in uncertainty is observed at the last step. The initial standard deviation is reduced by 52% for the 95th percentile, 60% for the 50th percentile and 56% for the 5th percentile. This is in clear contrast to pathway A, where the evaluation is based on the raw precipitation data.

River Discharge

The mean river discharge simulated under pathway A varies slightly after each deletion step (Fig. S1, first column). Similar to the groundwater head, when using the full set of metrics (9 m), the initial standard deviation increases for all of the steps. Again, the standard deviation of the ensemble decreases per step when using the other subsets of metrics (6 m and 3 m). For the 95th and 5th percentiles, using the 3 m subset results in the largest decrease in the initial standard deviation: 17% and 37%, respectively. For the 50th percentile, the standard deviation decreases the most when using 6 m, 36%.

In pathway B, the mean river discharge of the ensemble does not vary much after each step, for all subsets of metrics and percentiles analysed (Fig. S1, second column). For all subsets of metrics the standard deviation decreases after each step. For the 95th and 50th percentiles, the initial standard deviation is decreased the most when using all metrics (9 m), by 37% and 42%, respectively. The initial standard deviation of the 5th percentile is decreased the most when using six metrics (6 m), 55%.

Monthly Uncertainty Compared to other Weighting Approaches

Standard Deviation of the Monthly Projection

In Pathway A, the largests reduction in the standard deviation of the projection is obtained when the REA and UREA methods (Fig. 4a) are used. The methodology proposed here, evaluated by the 3 m subset, results in a larger standard deviation for most of the months, and from March to June its standard deviation is the same as that of the ensemble using all climate models (initial standard deviation). No clear difference in model performance is found for the REA and UREA methods. When assessing Pathway B, the methodology proposed here reduces the initial standard deviation the most for the majority of the months (Fig. 4b). Only from February to May, the REA method results in a smaller standard deviation.

Fig. 4

Uncertainty measures of the monthly mean river discharge considering the initial uncertainty compared to the uncertainty derived from the approach presented in this analysis (3 m for pathway A and 9 m for pathway B), REA and UREA: standard deviation of the projected monthly mean river discharge for a) pathway A, b) pathway B, and signal to noise ratio for the projected change in the monthly mean river discharge for c) pathway A and d) pathway B

Signal to Noise Ratio (SNR) of the Projected Monthly Change

In Pathway A, the method with the strongest SNR for each month varies (Fig. 4c). The 3 m subset has a stronger SNR for February, June, September and November. Overall, there is no method that consistently outperforms the others. When evaluating Pathway B, the 9 m subset of metrics consistently outperforms REA and UREA, providing a stronger SNR for 10 months (Fig. 4d). Only for September, UREA and REA had stronger SNR. For this month, the change in monthly mean river discharge is projected to be slightly negative.

Discussion

Methodology for a More ‘Realistic’ Uncertainty Assessment of the Hydrological Projections

The aim of the study is to obtain a more realistic uncertainty assessment of the projection of future hydrological variables by discarding climate models that do a relatively poor job in simulating the historical precipitation accurately. It is argued that for certain applications, a ‘behavioural uncertainty’ is useful to ease decision making and to decrease the computational burden that an impact assessment with a large climate model ensemble represents (Farjad et al. 2019). The idea behind evaluating the climate models in the historical period is that if a model has a low skill in the present, then it can be argued that its performance will be low in the future as well (Knutti 2008). However, we acknowledge that even if a good simulation skill is obtained in the present, it does not guarantee a good skill in the future (Knutti 2008; Reifen and Toumi 2009).

Previous studies have evaluated the simulation skill of climate models in the present to select or assign weights to an ensemble in hydrological impact studies (e.g., Wang et al. 2019; Chen et al. 2017; Seo et al. 2018). However, these studies evaluated the simulation skill of the mean or extremes independently, not in combination. This study goes beyond and combines metrics that assess the climate model skill to simulate mean, ‘moderate’ extreme and ‘highly’ extreme precipitation. Furthermore, the study compares the change in the uncertainty of the projections when using different subsets of metrics to determine whether there is a benefit from evaluating ‘moderate’ and ‘highly’ extreme metrics.

The methodology presented in this study appears to be a robust way of evaluating climate model projection uncertainties, providing results similar to approaches using weights and in some cases outperforming them (e.g. SNR for pathway B). By discarding non-behavioural climate models, the ensemble size is reduced, which is an advantage in cases with computationally demanding impact models. Furthermore, the method is applicable to different hydrological processes, such as river discharge and groundwater levels. The uncertainties of the low, mid and high percentiles of the analysed hydrological variables are reduced by the method at a similar extent. In principle, the method is easily reproducible because it is based on historical precipitation data that normally would be available. Nevertheless, the results might depend on the skill of the bias-correction method and on the metrics that are employed.

Selection of Metrics for Climate Model Evaluations

There is always a degree of subjectivity involved whenever assigning weights to climate models (Chen et al. 2017). This comprises selecting the evaluation metrics and choosing the weighting method (Christensen et al. 2010). Here, a set of metrics is used, involving the analysis of the annual mean and extreme precipitation. We acknowledge that the different extreme precipitation metrics might be correlated (Seo et al. 2018). However, we use different subsets of metrics that include means, variability, ‘moderate’ extremes and ‘highly’ extremes to evaluate the importance of each for the uncertainty of the projection.

No metrics considering the length of dry and wet spells are included. Such metrics could provide further understanding about the climate model capabilities, as observed by Seo et al. (2018). We argue that the set of metrics used is sufficient for a fair evaluation of the skills of the different climate models in a catchment which is driven mainly by precipitation.

In our case, the 3 m and 6 m subsets reduce the initial standard deviation the most following pathway A. Therefore, using basic metrics (means and ‘moderate’ extremes) for this pathway reduces uncertainty the most. In contrast, all metrics produce a higher reduction in the standard deviation when pathway B is evaluated. Thus, the metrics that are related to the ‘highly’ extreme events are relevant for reducing the uncertainty when bias-corrected climate models are evaluated. When compared, the final uncertainty is reduced more in pathway B than in pathway A. Thus, the evaluation based on the skill of the raw models is not valid after bias-correction and it can be argued that the bias-corrected projections are more robust than the raw outputs.

Evaluation Based on Raw or Bias-corrected RCM Data

Maraun and Widmann (2018) investigated the possible limitations of cross-validated bias-corrected free-running climate simulations against observations, which is the approach followed in pathway B. The main concern regarding this method is that the internal variability of the observations and simulations is not synchronized, possibly resulting in misleading results. Therefore, as a method for differentiating between the different climate models, they suggested to evaluate the skill of the uncorrected climate models considering temporal, spatial and process-based aspects.

Overall, the reduction in the hydrological uncertainty is larger for pathway B, which evaluates the bias-corrected models. This is likely to happen because the projections of hydrological variables used in the analysis are also based on bias-corrected outputs. In contrast, for Pathway A the evaluation and ranking is based on raw climate models, whose skill do not remain the same after they are bias-corrected. One could argue that the RCMs of Pathway A are not constrained by observed data (bias correction) and therefore can be expected to show a larger spread and a larger potential for reducing the spread by the ranking process. However, this is not the case and could be because the evaluation of the raw climate models does not succeed to identify the models that introduce a larger uncertainty to the hydrological projection after bias-correction.

Projection Uncertainties

Considering pathway B, by selecting the climate model ensemble based on an evaluation of different precipitation characteristics in the historical period, the uncertainty in the future hydrological projections is reduced. This is true for three different (high, median and low) percentiles of river discharge and groundwater head. The results of this analysis indicate that the uncertainty is reduced for each of the evaluated percentiles of the future period (2071–2100) as well as on a monthly basis. In contrast, for pathway A, the results do not show a clear change in the initial uncertainty when using each subset of metrics.

Additionally, the robustness of the results is confirmed by using three hydrological models with different conceptualizations of the unsaturated zone. This confirms that the above finding is not just an artefact of a single model but robust to different hydrological models that, as shown in Table S3, have different performance.

The projection uncertainty of the behavioural models in the ensemble depends on the metrics used to evaluate the simulation skill of the climate model. Here, the variation in uncertainty is larger for the last steps of the methodology. This might be because the models which projections differ the most from the projections of the remaining models in the ensemble are not discarded until the last steps, as shown by the spread depicted in Figs. 3 and S1. For both discharge and groundwater level, the projected mean does not change much after each step. Therefore, the method can be used to assess the change in projection uncertainty, while the projected mean is unaffected. It has been argued that the uncertainty in the projection can mainly be reduced by using bias-corrected models with equal-weighting (Wang et al. 2019). However, in our case, the uncertainty can be further reduced by removing the bias-corrected models that are poor at reproducing the historical precipitation.

Overall, this study indicates that the uncertainty of future conditions can be reduced following the methodology presented here, especially for pathway B and when using the 9 m subset of metrics as evaluation. Furthermore, the SNR results of the monthly mean change indicate stronger change signals from the approach presented here, compared to other methods (REA and UREA). These results should be tested for other contexts to evaluate their transferability.

Conclusions

Traditionally, impact assessments are based on the assumption that climate models have the same probability of occurrence. However, discarding poor-performing models from the ensemble can reduce the computational burden and affect the uncertainty of the projection. Previous research acknowledged that the large projection uncertainties negatively affect decision-making (e.g., Wilby and Harris 2006). In cases where the uncertainty is too large, the impact information is often disregarded for making any decision (Soares et al. 2018).

This study analyses the change in uncertainty of hydrological projections when the climate model ensemble is based on evaluating the simulation skill of the historical precipitation for a set of different evaluation metrics. The metrics used here evaluate the mean, variability, ‘moderate’ and ‘high’ extreme precipitation. The results indicate that when evaluating the raw climate models, there is not a clear link between the climate model ensemble selection and the uncertainty of the hydrological projection. When evaluating the bias-corrected climate models, the selected ensemble always reduced the hydrological uncertainty for different subsets of metrics, with a larger decrease when using all metrics.

It is relevant to assess whether the methodology is replicable elsewhere. Additionally, alternative evaluation approaches could be developed to rank the climate models and decrease the size of the ensemble. Such approaches could, for instance, assess the interdependence of the models (e.g. Evans et al. 2013; Pennell and Reichler 2011), the accurate simulation of precipitation trends or the accuracy of the simulation of global scale climate processes. Furthermore, other metrics could be used for evaluation, such as spatial–temporal metrics, which were not included in this analysis due to the relatively small size of the catchment. Similarly, it would be relevant to assess the potential of the method for other processes that could be driven by other climate factors than precipitation or more influenced by the structure of the impact model (e.g., soil moisture) (Her et al. 2019).

The results suggest that the uncertainty of future projections can potentially be reduced following the proposed methodology. Even though uncertainty reduction is encouraging seen from a decision-making point of view, it is acknowledged that the approach has the risk of hiding the uncertainty rather than reducing it (Chen et al. 2017). For instance, it is possible that a climate model with low historical simulation skill or with a significantly different climate change signal compared to the others, might project the changes in climate more realistically.