Abstract
This study hopes to develop a multi-criteria decision-making (MCDM) method for equitable and efficient allocation of water resources under scarcity. Based on the Bankruptcy problems, five classic plus one proposed allocation rules are introduced to generate water distribution alternatives. The “Core” solution of Cooperative Game Theory (CGT) and the Security Restriction have been used to select feasible alternatives. Additionally, five voting methods in Social Choice Theory (SCT) are launched to aggregate preferences and obtain a “win” alternative. Apply this model to the 2030 water allocation planning project of Ezhou City, China, as a case study. Under the proposed rule, Adjust minimal overlap rule (AMO), five regions, Urban Area, Gedian DZ, and three counties, hold the water deficit rate of 5.9%, 15.8%, and 4.7%-6.1%, respectively. In aggregating preferences by voting, AMO wins four out of five methods and takes second place in the last one, which provides some insights for allocating water fairly and feasibly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Water scarcity is becoming more prominent, with the intensification of global climate change and the acceleration of industrialization and urbanization (Salman 2007). In the past decades, human activities have caused the globally available water resources to decrease at a rate of about 100 billion \(m^3/year\) (Mueller Schmied et al. 2014; Wang et al. 2018). At the same time, global water consumption has increased six times in the past 100 years and is still growing steadily at a rate of approximately 1.0% per year (WWAP 2020). Uncontrolled water withdrawal and increased demand for fresh water are main causes of water shortages. Therefore, putting forward an equitable, reasonable, and sustainable water resource allocation manner is an effective way to solve the shortage of water resources.
Water resources management in a basin has changed from a single-goal problem into more complex multi-criteria decision making (MCDM) problems, which involve multiple features, multiple aspects, and multiple stakeholders (Huang et al. 2011; Gebre et al. 2021). Water is a fundamental resource for economic development, social welfare, and environmental protection. The allocation of water resources is a complex process that needs to meet the basic needs of agriculture, industry, and domestic use, as well as to maintain the balance of the ecosystem. At the same time, different water users have different preferences and characteristics, coordinating the conflicts of interests and demands among watershed stakeholders is a challenge for decision-makers.
Researchers try to solve the MCDM problems of water resources by using various methods, but defects are accompanied. The classical tools transform the MCDM problem into a single objective function and solve it through optimization algorithms (Harou et al. 2009). Although those methods can obtain optimal results theoretically, they still face low implement ability in practice because of their complex algorithms and abundant assumptions. Therefore, Game Theory (GT) has been introduced to describe the relationship between the individual and/or group rationality and to analyze the global equilibrium (Kaveh 2009; Thomson 2003). Even GT can better reflect the reality and provide foreseeable consequences, the reliable scenario requires accurate and large data, and proper determination of utility functions, which are often difficult to quantify (Kaveh 2009; Yu et al. 2019; Li et al. 2019; Lee 2012). Therefore, to maximize the comprehensive benefits of water resources allocation under MCDM, the following questions need to be answered: How to raise reasonable and realistic alternatives and how to choose them fairly and effectively, when data is scarce or utility functions are difficult to obtain?
1.1 Raise Alternatives
The Bankruptcy problems, coming from enterprise bankruptcy scenario, mainly study on how to distribute the remaining assets E, which is less than the claims C, among shareholders and creditors (O’Neill 1982). Distribution rules under Bankruptcy theory can offer equitable and reasonable solutions under limited resources, which has been widely used in many areas (Brink et al. 2013; Gimenez-Gomez and Penis 2014; Dietzenbacher et al. 2021). In water resource management, when the available water cannot meet the demands from basin users, how to efficiently and reasonably allocate water has a similar scenario with bankruptcy problems.
Several classic Bankruptcy rules have been proposed, under various interpretations of equity, which includes: Proportional rule (PRO), Constrained equal awards (CEA), Constrained equal losses (CEL), Piniles rule (Pin), the Talmud rule (TAL), Constrained egalitarian (CE), Adjust proportional (AP), Random arrival (RA) rule, and so on (Curiel et al. 1987; Mianabadi et al. 2014; Madani et al. 2014b; Thomson 2003). In addition to classic rules, two branches of Bankruptcy problems can be roughly extended: 1) weighted-based; 2) sequential-based. Considering the contribution and corresponding claims, scholars re-determine the weight of each stakeholder by introducing coefficients or vectors from different standards (Mianabadi et al. 2015), like marginal contribution to the coalition (Degefu et al. 2016), willingness to pay criterion (Sechi and Zucca 2015), multiple hydrological constraints (Yong et al. 2017), to adjust equitable consequences. Meanwhile, other scholars have considered spatial variability of river basins users, Ansink and Weikard (2012) transfer a basin-based bankruptcy problem to a linear order two-agent sharing problem, and Goetz et al. (2008) define two different sequential allocation rules that respect asymmetry. In recent years, many studies integrate Bankruptcy theory with other game-based theories to explore new allocation methods: Degefu et al. (2016) systematically combine Bankruptcy framework with the Bargaining theory, Yuan et al. (2017) construct a cooperation bankruptcy game model, and Yazdian et al. (2021) develop a non-cooperative optimal management scenario under bankruptcy conditions. In practice, we found that current Bankruptcy rules mostly sets water allocation weights when facing economic factors, while insufficiently considering the details and differences of participants that are reflected by the factors. Failure to consider the characteristics and constraints of the sectors (agriculture, industry, domestic, etc.) in each region may lead to a gap between theory and reality.
To solve this problem, we propose a novel distribution rule, the Adjusted minimal overlap rule (AMO), based on the Bankruptcy theory, which takes into account the different characteristics of participants while ensuring fairness. Then, we propose a new restriction, the Security Restriction, which considers the influence of different economic factors to determine whether the alternatives are feasible.
Applying Bankruptcy rules to water resources allocation has the following advantages: 1) Bankruptcy rules provide fair and reasonable allocations to the riparian stakeholders. 2) They are game-theoretic-based methods, which can reflect the individual preference and group rationality of stakeholders. 3) They are well understood, easily implemented, which is more valuable for solving actual water conflict.
1.2 Choose Alternatives
Social Choice Theory (SCT) studies the relationship between individual preferences and group choices, which can be considered as a voting technique that belongs to MCDM (Madani et al. 2014b). Due to few requirements and a concise voting process, SCT has been widely accepted in scenarios with incomplete information or unknown utility functions. By designing a voting process, individual preferences are aggregated into a collective decision, and the “win” alternative is selected (Feldman and Serrano 2006).
Water resources are managed by different stakeholders who have different characteristics and interests. Considering the heterogeneity of stakeholders, centralized optimization models cannot well reflect the individual preferences, and game-based models insufficient consideration of the group decision-making process, which reduces the motivation of agents to participate and leads to deviations. SCT can evaluate and rank different water resources allocation alternatives based on the preferences of stakeholders. Although the result may not be Pareto optimal, SCT can aggregate consensus among stakeholders and reach an acceptable and implementable solution (Read et al. 2014).
The advantages of SCT in water resources management can be summarized as follows: 1) Relatively simple and clear rules, which suitable for MCDM problems. 2) Concise voting process does not rely on detailed data and utility functions, which is particularly attractive when information is uncertain. 3) Well participation of stakeholders provides better acceptability and stability, which is especially valuable for resolving conflicts under scarcity scenarios.
1.3 Innovation and Structure
In response to the questions raised previously, this research aims to make water resource allocation decisions in an equitable, reasonable, and sustainable manner, in the case of insufficient data or the utility function is unavailable. The highlights of this paper can be summarized as follows:
-
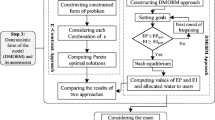
Propose a model that can solve the above problems, which mainly includes three steps: raising, filtering, and choosing alternatives (see Fig. 1 for details).
-
Based on the Bankruptcy theory, we propose a novel distribution rule (the AMO rule) that takes into account the different characteristics of participants while ensuring fairness.
-
Propose a new constrain measure, the Security Restriction, to find the feasible solutions, together with the “Core” Solution in the Cooperative Game Theory (CGT).
-
Five voting methods, base on SCT, are launched to aggregate preferences and to obtain a “win” alternative in different situations
Apply this model to water resource planning problems of Ezhou City, Hubei Province, China as a case study. This study provides a concise and efficient decision-making solution for the multi-agent decentralized MCMD problem under the condition of insufficient information.
This paper organizes in the following structure: Sect. 2 mainly defines and describes the model, which consists of three parts. The first part describes the basic rules of Bankruptcy and proposes the new rules, the second part takes the economic factors as constraints to ensure feasibility, the last part introduces the aggregating process under SCT. A case study application of the three parts is described in Sect. 3. The results and discussion of the model application will be presented in Sect. 4. The last Sect. 5 presents a summary of the study.
2 Methodology
The flowchart below illustrates the methodology of this research (see Fig. 1) and the following sections discuss the methods involved in the model.
2.1 Bankruptcy Allocation Rules
This subsection generates alternatives through Bankruptcy rules. We use five widely accepted rules (PRO, AP, CEA, CEL, and TAL) and one proposed rule (Adjusted minimal overlap rule, AMO) for water resource allocation.
2.1.1 Basic Scene
Consider a total amount E of water resource available for distribution among a set of agents \(N=(1,2,...,n)\) in the river basin. The claims of each agent are \(c_i\ge 0\) for, and the sum for their claims C exceed E (\(C \ge E\)).
The Bankruptcy problem in basin system can be defined as \(\Psi (N,E,c)\), and the objective is to determine the allocation amount of each agents, denoted by \(x_i\), where \(x=(x_1,x_2,...,x_n)\). There are three basic requirements for the Bankruptcy problems:
Requirement(a), “efficiency”
the sum of all resources should not exceed the amount available and the entire amount available should be allocated (Thomson 2003).
Requirement(b), “non-negativity and feasibility”
each agent should receive a non-negative amount and should not be larger than his claims (Mianabadi et al. 2014; Mianabadi et al. 2015).
Requirement(c), “equal treatment and monotonicity”
same claims receive the same treatment, and the amount of allocations should be positively correlated with the claims (Thomson 2003).
For each \((N,E,c)\in \Psi\) and each \(\{ i , j \}\in N\):
2.1.2 Classic Rules
-
1.
Proportional rule, PRO, is the most commonly used rule in practice, and its allocation principle is to allocate water resources according to a fixed proportion \(\lambda\) of claims in each agent:
$$\begin{aligned} P R O ( x _ { i } ) =\lambda x _ { i } \quad where \quad \lambda = \frac{ E }{ C } \end{aligned}$$(7)in which, \(PRO(x_i)\) stands for the allocation \(x_i\) of each agent under the proportional rule, follows are same.
-
2.
Adjusted proportional rule, AP, can be considered to ensure the minimal right of agents first, and then the PRO rule is launched on the remainder.
For \((N,E,c) \in \Psi\) and each \(\{i,j\} \in N\), the minimal right of agents can be defined as:
$$\begin{aligned} m _ { i } ( E , c ) = m a x \{ E - \sum_{ j \in N \Vert \{ i \} } c _ j, 0 \} \end{aligned}$$(8)Then the AP rule:
$$\begin{aligned} A P ( x _ { i } ) = m _ { i } ( E , c ) + P R O ( c _ { i } - m _ { i } ( E , c ) ) \end{aligned}$$(9) -
3.
Constrained equal awards rule, CEA, takes “equal” as primary, assigns equal amounts to all agents, subject to no one exceeding his claims:
$$\begin{aligned} C E A ( x _ { i } ) = min \{ c _ i , \lambda \} \quad where \quad \sum m i n \{ c _ i, \lambda \} = E \end{aligned}$$(10)in which, \(\lambda\) represents an equal share of total amount E.
-
4.
Constrained equal losses rule, CEL, also takes “equal” as primary but on anther side, assigns equal loss to all agents, constrained to no claimant receiving a negative allocation:
$$\begin{aligned} C E L ( x _ { i } ) = max \{ 0 , c_i - \lambda \} \quad where \quad \sum max \{ 0, c _ i- \lambda \} = E \end{aligned}$$(11)in which, \(\lambda\) represents an equal loss of agents.
-
5.
Talmud rule, TAL, generated by Aumann and Maschler (1985), draws on the half-sum idea. Determine whether the amount to divide (E) equals half of the claims (C/2) firstly. If there is less, the CEA formula is applied; and if there is more, the CEL is launched. In each case, the half-claims are used in the formula instead of the claims themselves (Thomson 2003):
if \(\sum ( \frac{ c _ { i } }{ 2 } ) >E\), then:
$$\begin{aligned} T A L ( x_i ) = m i n \{ \frac{ c _ { i } }{ 2 } , \lambda \} \quad where \quad \sum min \{ c _ { i } / 2 ,;\,\lambda \} = E \end{aligned}$$(12)if \(\sum ( \frac{ c _ { i } }{ 2 } ) \le E\), then:
$$\begin{aligned} T A L ( x_i ) = c_i - m i n \{ \frac{ c _ { i } }{ 2 } , \lambda \} \quad where \quad \sum [ c_i - min \{ c _ { i } / 2 , \lambda \} ]= E \end{aligned}$$(13)
2.1.3 The Proposed Rule
Adjust minimal overlap rule, AMO
is inspired by the Minimal overlap rules (MO) mentioned by O’Neill (1982). The disadvantage of the MO rule is that it can only be applied when the assets are no more than the maximum claim and no less than the minimum claim, which leads to insufficient applicability. We put forward an improvement on MO, taking the total water deficits \((C-E)\) as “assets” and applying MO rules to allocate them. The water allocation \(x_i\) of each agent equals to its claim \(c_i\) minus its share of the deficit \(D_i (c)\), calculation steps are following:
-
(a)
Sort claims from small to large, and the new sequence marked as \(k = 1,2,...,N\).
-
(b)
Divide the deficit \((C-E)\) according to specific “units”, so that the number of units claimed by agent \(k=N\) is maximized. Then, the size of each “unit” can be expressed as \(u=\frac{C-E}{c_n}\).
-
(c)
Distribute claims over these units to minimize overlap claims of the “assets” . For each “unit” , equal division prevails among all agents claiming it. Denote the deficits shared by agent k as \(D_k(C), k \in N\), then:
$$\begin{aligned} {\left\{ \begin{array}{ll} D _ { 1 } ( c ) = \frac{ c _ { 1 } }{ n } \times u\\ D _ { 2 } ( c ) = ( \frac{ c _ { 2 } - c _ { 1 } }{ n - 1 } + D _ { 1 } ( c ) ) \times u\\ \qquad \vdots \\ D _ { k } ( c ) = ( \frac{ c _ { k } - c _ { k-1 } }{ n-k+1 } + D _ { k-1 } ( c ) ) \times u\\ \qquad \vdots \\ D _ { n } ( c ) = ( \frac{ c _ { n } - c _ { n-1 } }{ 1 } + D _ { n-1 } ( c ) ) \times u \end{array}\right. } \end{aligned}$$(14) -
(d)
The amount of water allocation to each agent is its claims minus its share of deficit:
$$\begin{aligned} A M O ( x_k ) = c_k - D_k (c) \end{aligned}$$(15)
2.2 “Core” Solution and Security Restrictions
-
1.
“Core” Solution
The Bankruptcy problems arise for total claims exceeding the available resources, which can be considered as a branch of CGT that determine the fair allocation of assets among different agents (Aumann and Hart 1992). CGT provides the necessary instruments to determine how benefits or assets can be fairly and efficiently distributed among agents, and where are the boundaries of grand coalitions or cooperation remain stable, called the “Core” solution. To define a CGT, additional definitions are following:
-
\(x_i\) represent the benefit when agent i cooperate with others;
-
\(x_i^*\) represent the benefit when agent i act alone;
-
\(S \in N\) is a “coalition” , when S=N is the “grand coalition” ;
-
v(S) is the benefit linked to the coalition S;
-
v(N) is the benefit linked to the grand coalition.
To obtain a “Core” solution, CGT exploits three fundamental principles:
The Efficiency, the benefits of the coalition are all distributed among its participants.
$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _ { i \in N } x _ { i } = v ( N ) \\ \sum _ { i \in S } x _ { i } = v ( S ) \end{array}\right. } \end{aligned}$$(16)The Coalition Rationality, no agent or coalition gain benefit less than its standalone benefit:
$$\begin{aligned} \sum _ { i \in S } x _ { i } ^ * \le v ( S ) \end{aligned}$$(17)The Individual Rationality, for each agent, cooperative is no less than not
$$\begin{aligned} x _ { i } \ge x _ { i } ^ * \end{aligned}$$(18)Sechi and Zucca (2015) establishes the connection between CGT and Bankruptcy problems in water resources allocation by treating the water allocation \(x_i\) as the benefits in CGT, so we have: \(v(N) = E\) for Eq. (16).
Here, we refer Sechi and Zucca (2015) definition of the “Core” solution characteristic function:
$$\begin{aligned} v ( S ) = m a x \{ ( E - \sum _ { i \in ( N - S ) } c _ { i }) , 0 \} ,\quad S \in N \end{aligned}$$(19)Take the “Core” solution of CGT as one of the restriction conditions of the water allocation alternatives.
-
-
2.
Security Restriction
The “Core” solution ensures that participants can get more benefits in the grand coalition and maintain cooperation, but it does not mean that the alternatives will be accepted automatically. Different departments have different security requirements (tolerance of water deficit rate), and the economic factors of regions are different as well. At the same time, the same amount of water shortage has less impact on larger water users (low deficit ratio), and different sectors (agriculture, industry, domestic, etc.) have different tolerance of deficit ratios. Failure to take into account the characteristics and constraints of regions and sectors may lead to infeasible alternatives.
Combining the two aspects of economic factors, economic volume (represented by total water demand) and economic structure (represented by tolerance of water deficit), we propose another constraint: the security restriction. This study regards the maximum tolerance for water deficits as the bottom line, considers the economic structure of agriculture, industry, and domestic in each region, and sets the Security Restriction as follows:
$$\begin{aligned} c _ { i } - x _ { i } = D _ { i } ( c ) \le d _ { i } ^ { a g r } + d _ { i } ^ { i n d } + d _ { i } ^ { d o m } \end{aligned}$$(20)In which, \(d _ { i } ^ { a g r } , d _ { i } ^ { i n d } , d _ { i } ^ { d o m }\) represents the maximum allowable deficit of agriculture, industry, and domestic water for region i , respectively.
2.3 Aggregate Preference under Social Choice Theory
SCT may be regarded as concise and efficient decision-making tools that enhance the stability or acceptability of group endeavors (Srdjevic 2007; Zolfagharipoor and Ahmadi 2016; Madani et al. 2014a). The basic problem in the water resource allocation area is to design a reasonable voting method on given water resource allocation alternatives. Voters (stakeholders) state their preferences for each alternative assuming that they have equal powers. Social Choice rules are launched to aggregate voters’ preferences and produce the “win” alternative based on each specific notion of social optimality and fairness.
Here, five popular and practical voting processes are introduced to the water allocation problem which includes: Plurality voting (PV), Hare system (HS), Borda count (BC), Pairwise comparisons voting (PC), Approval voting (AV).
2.3.1 Basic Scene
A general mathematical formulation of Social Choice problems can be denoted in the following way:
Considering there are n stakeholders and m alternatives, stakeholders rank the alternatives based on their preferences (or utility functions). Therefore, a preference odder matrix \(R_ {n \times m }\) can be constructed as below:
In which, \(r _ {i,j}\) represents the preference ranking value of stakeholder i for alternative j. If j is the best alternative for stakeholder i, then \(i _ {i,j} = 1\); If j is the second best alternative for stakeholder i , then \(i _ {i,j} = 2\), and so on; for the worst alternative, then \(i _ {i,j} = n\).
2.3.2 Voting Methods
-
1.
Plurality voting, PV, is one of the oldest and perhaps the most commonly used method (Madani et al. 2014a). Based on the plurality rule, the “win” solution is the alternative with the largest number of first-place rankings:
Define:
$$\begin{aligned} p( r _ {i,j} ) = {\left\{ \begin{array}{ll} 1 &{} if \quad r _ {i,j} = 1\\ 0 &{} otherwise \end{array}\right. } \end{aligned}$$(22)For each alternative j, the sum:
$$\begin{aligned} P _ { j } = \sum _ { i = 1 } ^ { N } p ( r _ { i j } ) \end{aligned}$$(23)The number of \(P _ j\) indicates how many times alternative j has been chosen as the best, and the “win” alternative \(P V _ j\) under the Plurality voting rule is:
$$\begin{aligned} P V _ { j } = m a x \, { P _ j } \end{aligned}$$(24) -
2.
The Hare system, HS, is based on the successive deletion of less desirable alternatives (D’Angelo et al. 1998). After each round of voting, the alternative with the least votes is eliminated and a new round of voting is done with the remaining alternatives until there is an alternative that gets more than half of the votes or all remaining alternatives get equal votes.f
For M alternatives election, the Hare system requires \(M - 1\) rounds at a maximum.
At each step, the deleted alternative \(j ^ *\) is selected as:
$$\begin{aligned} P _ {j ^ *} = m i n\,{P _ j} \end{aligned}$$(25)where \(P _ j\) are defined in the Plurality rule (see Eq. 23). After deleting the least desirable alternative, the preference odder matrix changes to \(R _ {n \times (m -1) }\) and preference ranking value \(r _ {i,j}\) of stakeholder i modify as:
$$\begin{aligned} r _ {i,j} ^ { new } = {\left\{ \begin{array}{ll} r _ {i,j} &{} if \quad r _ {i,j} \le r _ {i,j ^ *}\\ r _ {i,j} - 1 &{} otherwise \end{array}\right. } \end{aligned}$$(26)The process terminates, the “win” alternative \(HS _ j\) under the Hare system voting rule when:
$$\begin{aligned} H S _ j = {\left\{ \begin{array}{ll} P _ {j} \ge \frac{M}{2} \\ P _ {j} &{} \text{when}\;P_{j}\;\mathrm{equals\;to\;each\;other} \end{array}\right. } \end{aligned}$$(27) -
3.
The Borda count, BC, follows the highest point to “win” . In this method, every alternative receives a point according to its rank for each stakeholder. When a lower rank means a better preference, the worst alternative gets 0 points, the second-worst gets 1 point, and so on, the very best alternative gets points.
If \(a _ {i,j}\) is preference point, then:
$$\begin{aligned} a _ { i ,j } = m - r _ { i ,j } \end{aligned}$$(28)Hence, the total point for each alternative j is:
$$\begin{aligned} P _ { j } = \sum _ { i = 1 } ^ { n } a _ { i, j } = n m - \sum _ { i = 1 } ^ { n } r _ { i ,j } \end{aligned}$$(29)And the “win” alternative \(BC _ {j}\) under the Borda count rule is:
$$\begin{aligned} BC _ { j } = max \ { P _ j } \end{aligned}$$(30) -
4.
Pairwise comparisons voting, PC, match alternatives with each other head-to-head (Srdjevic 2007; Ghodsi et al. 2016). Each alternative gets 1 point for a one-on-one win and a half a point for a tie. The alternative with the most total points is the winner.
For each ordered pair \(j_1,j_2\) of alternatives, let the number of stakeholders who prefer \(j_1\) than \(j_2\) denoted by \(N ( j_1,j_2 )\). The overall \(j_1\) is preferred to \(j_2\) if:
$$\begin{aligned} N ( j _ { 1 } , j _ { 2 } ) \succ N ( j _ { 2 } , j _ { 1 } ) \end{aligned}$$(31)And the compare point \(b _ {g,h}\) is:
$$\begin{aligned} b _ {g,h} = {\left\{ \begin{array}{ll} { 1 } &{} if \quad N ( j _ g , j _ h ) \succ N ( j _ h , j _ g ) \\ { 0.5 } &{} if \quad N ( j _ g , j _ h ) \equiv N ( j _ h , j _ g ) \\ { 0 } &{} if \quad N ( j _ g , j _ h ) \prec N ( j _ h , j _ g ) \end{array}\right. } \end{aligned}$$(32)where: \(g \ne h\) and \(g, h \in \{ 1,2,...,m\}\).
Then, a preference matrix \(P _ {m \times m}\) can built by compare point \(b _ {g,h}\):
$$\begin{aligned} P _ {m \times m} = \begin{pmatrix} { - } &{} b_ {1,2} &{} \cdots &{} b_ {1, m-1} &{} b_ {1,m} \\ b_ {2,1} &{} { - } &{} \cdots &{} b_ {2, m-1} &{} b_ {2,m} \\ \vdots &{} \vdots &{} { - } &{} \vdots &{} \vdots \\ b_ {m-1,1} &{} b_ {m-1,2} &{} \cdots &{} { - } &{} b_ {m-1,m} \\ b_ {m,1} &{} b_ {m,2} &{} \cdots &{} b_ {m, m-1} &{} { - } \end{pmatrix} \quad where \quad b_{g,h} + b_{h,g} = 1 \end{aligned}$$(33)For each alternative j, the sum of compare point is:
$$\begin{aligned} P _ { j } = \sum _ { g = 1 } ^ { m } b _ { g , j } \end{aligned}$$(34)The “win” alternative \(PC _ j\) under the Pairwise comparisons rule is:
$$\begin{aligned} P C = m a x \ \{ P _ { j } \} \end{aligned}$$(35) -
5.
Approval voting, AV, is a method of voting in which stakeholders can vote for (approve for) as many alternatives as they wish (Brams and Fishburn 1978). Similar to the plurality rule, ranking of options is not required, but the certain number \(l \ ( l < m )\) of the approved-group needs to be determined. The alternative that has the largest number of approved votes will “win”.
Mathematically, this concept can be formulated as follows:
Define:
$$\begin{aligned} p _ (r _ {i,j}) = {\left\{ \begin{array}{ll} 1 &{} if \quad r _ {i,j} \le \rho \\ 0 &{} otherwise \end{array}\right. } \quad where \quad 1 < \rho \le l \end{aligned}$$(36)For each alternative j the sum:
$$\begin{aligned} P _ { j } = \sum _ { i = 1 } ^ { N } p ( r _ { i ,j } ) \end{aligned}$$(37)The number of \(P _ j\) indicates how many times alternative j has been approved, and the “win” alternative \(AV _ j\) under the Approval voting rule is:
$$\begin{aligned} A V _ { j } = max \ \{ P _ { j } \} \end{aligned}$$(38)There is no single voting method that works for all MCMD problems, nor is there “the best” method. Researchers need to choose the appropriate voting methods based on the specific problem they face. This paper makes a preliminary discussion on the advantages and disadvantages of the above five methods, as shown in Table 1.
3 Case Study
This section applies the proposed model to the 2030 water resources allocation planning of Ezhou City (China), where the water supply is less than the claims of stakeholders. Initially, the General Water Allocation and Simulation Model (GWAS) is applied to simulate the natural-social water cycle process. Then, the water allocation alternatives are raised based on the Bankruptcy theory. Use the “Core” solution of CGT and the Security Restriction to test the feasibility of alternatives. Finally, with five SCT voting methods, the preferences are aggregated, the ”win” alternatives are selected, and the results are analyzed and discussed.
3.1 Study Area
Ezhou City is located in the southeast of Hubei Province, China, with a total area of 1,594 \(km^2\), including five regions: the Urban Area, Gedian Development Zone (Gedian DZ), and three counties (Echeng, Huarong, and Liangzihu). The main source of water supply in the study area is the Yangtze River, which flows through the northern part of Ezhou City (see Fig. 2). The five regional governments of Ezhou City will be regarded as stakeholders in the issue of water resource allocation.
3.2 Problem Description
According to data from Ezhou Comprehensive Planning of Water Resources, Ezhou City Water Resources Bulletin, and Statistical Yearbook of Hubei Province, the estimation of total water demand in Ezhou City will reach \(1196.85 {Mm^3}/{year}\) in 2030, including \(304.75 {Mm^3}/{year}\) for agriculture, \(649.79 {Mm^3}/{year}\) for industry and \(242.32 {Mm^3}/{year}\) for domestic use. However, by 2030, the planned water supply capacity of Ezhou City is only \(1,080.02 {Mm^3}/{year}\), with a deficit of \(116.83 {Mm^3}/{year}\). After determining the maximum water withdrawal, the five stakeholders negotiate quotas based on their respective development plans and economic predictions. As the total amount of claims by water users exceeds the available supply, the water resources planning can be characterized as a Bankruptcy problem. At the same time, how to allocate water resources equitably and efficiently is a challenge for decision-makers as there is little measurable data available for future scenarios.
Stakeholders have different water claims, details are illustrated in Table 2. From the perspective of water use structure, since the residents are mainly live in the Urban Area, domestic water and light industrial water are dominant. Heavy industrial enterprises are concentrated in Gedian DZ, resulting in 63.45% of the total industrial water consumption in this region. The three counties of Echeng, Huarong, and Liangzihu have well-developed planting and irrigation systems, which are the main bodies of agricultural water use.
In water resource allocation planning, each region hopes to minimize the deficit of its own water claims; but due to the different economic structures, different regions have different maximum allowable deficit rates. Domestic water, as the basic social security resource, has the highest security requirements and the upper limit of the deficit rate is 5.0%. Industrial water requires a high level of water supply stability, and the water deficit rate needs to be below 15.0%. Agricultural water is relatively flexible according to weather conditions (which are unpredictable), so this study controls the deficit rate to 50.0%.
3.3 Water Allocation and Simulation
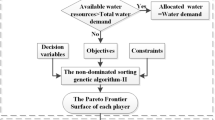
In order to better analyze the situation of regional water resources in the future scenario (2030), the General Water Allocation and Simulation model (GWAS) is launched for water resources simulation and management. GWAS is further developed from the Water resources Allocation and Simulation model (WAS) (Sang et al. 2018), which contains a variety of functions, including regional water use and drain, reservoir operation, power generation, ecological flow, economic analysis, and so on (Wang et al. 2014; Zhai et al. 2017; Yan et al. 2020). With the help of two algorithms (the rule algorithm and NSGA-II algorithm) and a multi-objective calculation scheme, this model can dynamically simulate the “natural-artificial” water cycle influenced by nature and human beings (see Fig. 3).
4 Results and Discussion
4.1 Bankruptcy Alternatives
Starting with the previous definition, we applied PRO, AP, CEA, CEL, TAL, and AMO (the proposed) allocation rules for water distribution, respectively, results are reported in Table 3.
In the water allocation alternatives, CEL and TAL results are the same, which is not surprising since the algorithms for CEL and TAL are equal when the water supply is greater than half of the total water claims. Gedian DZ is the least affected (deficit rate of 4.7%) due to its largest water claim, while the three counties have relatively serious water shortages (deficit rates of 18.5%, 10.6%, 16.5%, respectively). However, under the CEA rules, Gedian DZ will bear all the losses (deficit rate of 23.7%), also because the water demand is the largest, while the rest of the regions are completely satisfied.
The AP rule is noteworthy because we found that if the minimum rights of all stakeholders are non-zero, the AP allocation results will be consistent with the CEL. The reason is that a non-zero minimum right of all participants will result in the distributable water shares being clearly divided into two parts: an undisputed part (claimed by only one participant) and a disputed part (all participants claim against it). When comes to the second stage, the PRO rule is applied to the disputed part, causing this part to be divided equally, making the final value equal to CEL (see Eq. 9).
The AMO rule makes the deficit “shared but differentiated” among all participating stakeholders: the greater the water claim, the larger the water deficit. Since Huarong and Liangzihu counties have low water demand, their losses are also small (5.1% and 5.9% of the total deficit, corresponding to 4.7% and 4.9% of the deficit rate). Gedian DZ consumes 41.3% of the total allocatable water, causing it to bear the largest share of the shortage (66.7% of the total deficit), but with a deficit ratio of only 15.8%, which is lower than CEA and higher than CEL. The distribution of AMO rules is relatively moderate, avoiding extreme situations and making participants more inclined to reach a deal.
4.2 Feasible Test
The principles of Efficiency, Coalition, and Individual Rationality define the “Core” of the Cooperative Game solutions (Sechi and Zucca 2015), representing fairness and efficiency, meaning the solution is feasible for all stakeholders (Degefu and He 2016; Degefu et al. 2018). Use the “Core” as one of the constraints of the Bankruptcy alternatives, which refers that individuals cannot obtain more water resources through non-cooperation or partial coalition (See Eqs. 16–19). At the same time, the Security Restriction are also raised, because we cannot ignore the tolerance level of the regional economic structure for water scarcity (See Eq. 20).
In Table 4, the “Core” solution and security restriction ranges are shown. A water allocation alternative within the upper and lower limits can be considered as feasible for all stakeholders. For this Bankruptcy problems with five stakeholders, two constraints can be represented graphically by an equilateral pentagon with heights standing for the deficit rate of each participants, show in Fig. 4.
In this study, it is not difficult to find that the security restrictions are more stringent than “Core” solutions, and differences vary from region to region. All alternatives fit into the ”Core” solutions, which means that participants cannot obtain greater benefits through non-cooperation or acting alone. But the ”Core” does not mean that alternatives will be automatically accepted, and regional policymakers must also consider their own development needs and basic water security requirements when making decisions.
As can be seen in Fig. 4, although the CEA rule complies with the “core” solution, it will still be rejected by the Gedian DZ. The security requirements for domestic and industrial water are much higher than for agricultural water, resulting in a lower tolerance for water shortage in densely populated or industrially concentrated areas. This difference in economic structure narrows the scope of the Security Restrictions in the Urban Area and Gedian DZ.
Ultimately, within these two constraints, the acceptable solutions are PRO, AP, CEL, TAL, and AMO (the proposed). These five alternatives will undergo the preferences aggregation process to determine the final “win” alternative.
4.3 Social Choice Selection
SCT, as a concise and effective MCDM tool, can properly design the voting process, aggregate the opinions of the participants, and reach a consensus. Although the result is not necessarily Pareto optimal, it is more acceptable to stakeholders (Read et al. 2014). Use five voting methods, PV, HS, BC, PC, and AV, to aggregate preferences for all the alternatives that satisfy the constraints. The results are shown in Table 5.
It’s easy to find that the AMO rule came first in the PV, HS, BC, and PC voting process, while the PRO rule was the most popular under the AV method. The PRO wins in the last method due to its “good” (second priority) rating from all participants and gets points for any cases that the size of approved-group larger than two (\(l \ge 2\)). The AMO rule ensures that all participants share the deficit, but they are treated differently according to their respective circumstances, making it easier to reach a consensus. Although it is slightly worse than PRO in the AV process (2nd place), the AMO solution still has very stable and fair performance and can be considered as the most widely accepted (maximum probability) method.
5 Conclusion
This study hopes to develop a water resource allocation management method when data is lacking or utility functions cannot be obtained. Based on Bankruptcy Theory, five classic allocation rules for water resources planning and management are introduced, and a new allocation rule under water scarcity is proposed. The main feature of the proposed rules is to benefit the interests of disadvantaged groups while guaranteeing fairness and efficiency. In addition, we use the “core” solution from CGT and the Security Restrictions to ensure the acceptability. Finally, five different voting processes under the SCT have been launched to aggregate the preferences of the alternatives and obtain the “win” solution. We use the water resources allocation planning of Ezhou City, Hubei Province, China, as a case study to discuss the water resources allocation problems when data is scarce or utility functions are difficult to obtain.
Six allocation rules (PRO, AP, CEA, CEL, TAL, and AMO), according to different principles, propose six different allocation scenarios for the water resources planning project in Ezhou City. Although all the alternatives are keeping in line with the “Core” solution, CEA has been excluded due to the Security Restriction of Gedian DZ. The proposed rule, AMO, holds the water deficit rate of Urban Area, Gedian DZ, and three counties are 5.9%, 15.8% and 4.7%–6.1%, respectively. In the process of aggregating stakeholder preferences and selecting the “win” solution, the AMO rule won four out of five SCT-based voting methods and came second in the fifth. Therefore, research shows that AMO has certain advantages in obtaining fair and efficient solutions in the case of water scarcity.
Like most studies, this paper also has shortcomings and regrets. Limited by the research conditions and data, we have studied water supply and demand management, but only analyzed the regional water use pattern under the water scarcity from the perspective of economic structure. Other economic factors, like water benefits and costs, were under-considered, and this regret will further expend in the follow-up researches.
In short, the proposed allocation model can allocate water resources in a situation of scarcity fairly and effectively, and provide a reference for solving the MCMD problem.
References
Ansink E, Weikard HP (2012) Sequential sharing rules for river sharing problems. Soc Choice Welfare 38(2):187–210. https://doi.org/10.1007/s00355-010-0525-y
Aumann R, Hart S (1992) Handbook of game theory with economic applications. Tech Rep. https://doi.org/10.2307/2234489
Aumann RJ, Maschler M (1985) Game theoretic analysis of a bankruptcy problem from the talmud. J Econ Theory 36(2):195–213. https://doi.org/10.1016/0022-0531(85)90102-4
Brams SJ, Fishburn PC (1978) Approval voting. Am Political Sci Rev 72(3):831–847. https://doi.org/10.2307/1955105
Brink R, Funaki Y, Gerard V (2013) Characterization of the reverse talmud bankruptcy rule by exemption and exclusion properties. Eur J Oper Res 228(2):413–417. https://doi.org/10.1016/j.ejor.2013.01.052
Curiel IJ, Maschler M, Tijs SH (1987) Bankruptcy games. Zeitschrift Für Oper Res 31(5):A143–A159. https://doi.org/10.1007/BF02109593
D’Angelo A, Eskandari A, Szidarovszky F (1998) Social choice procedures in water-resource management. J Environ Manag 52(3):203–210. https://doi.org/10.1006/jema.1997.0156
Degefu DM, He W (2016) Allocating water under bankruptcy scenario. Water Resour Manag 30(11):3949–3964. https://doi.org/10.1007/s11269-016-1403-x
Degefu DM, He W, Yuan L et al (2016) Water allocation in transboundary river basins under water scarcity: a cooperative bargaining approach. Water Resour Manag 30(12):4451–4466. https://doi.org/10.1007/s11269-016-1431-6
Degefu DM, He W, Yuan L et al (2018) Bankruptcy to surplus: Sharing transboundary river basin's water under scarcity. Water Resour Manag 32(8):2735–2751. https://doi.org/10.1007/s11269-018-1955-z
Dietzenbacher B, Estevez-Fernandez A, Borm P et al (2021) Proportionality, equality, and duality in bankruptcy problems with nontransferable utility. Ann Oper Res 301(1-2SI):65–80. https://doi.org/10.1007/s10479-020-03643-3
Feldman AM, Serrano R (2006) Welfare economics and social choice theory. Springer Science & Business Media
Gebre SL, Cattrysse D, Van Orshoven J (2021) Multi-criteria decision-making methods to address water allocation problems: a systematic review. Water 13(1252). https://doi.org/10.3390/w13020125
Ghodsi SH, Kerachian R, Zahmatkesh Z (2016) A multi-stakeholder framework for urban runoff quality management: Application of social choice and bargaining techniques. Sci Total Environ 550:574–585. https://doi.org/10.1016/j.scitotenv.2016.01.052
Gimenez-Gomez JM, Penis JE (2014) A proportional approach to claims problems with a guaranteed minimum. Eur J Oper Res 232(1):109–116. https://doi.org/10.1016/j.ejor.2013.06.039
Goetz RU, Martinez Y, Rodrigo J (2008) Water allocation by social choice rules: the case of sequential rules. Ecol Econ 65(2):304–314. https://doi.org/10.1016/j.ecolecon.2007.06.018
Harou JJ, Pulido-Velazquez M, Rosenberg DE et al (2009) Hydro-economic models: Concepts, design, applications, and future prospects. J Hydrol 375(3–4):627–643. https://doi.org/10.1016/j.jhydrol.2009.06.037
Huang IB, Keisler J, Linkov I (2011) Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Sci Total Environ 409(19):3578–3594. https://doi.org/10.1016/j.scitotenv.2011.06.022
Kaveh M (2009) Game theory and water resources. J Hydrol 381(3). https://doi.org/10.1016/j.jhydrol.2009.11.045
Lee CS (2012) Multi-objective game-theory models for conflict analysis in reservoir watershed management. Chemosphere 87(6). https://doi.org/10.1016/j.chemosphere.2012.01.014
Li D, Zhao J, Govindaraju RS (2019) Water benefits sharing under transboundary cooperation in the lancang-mekong river basin. J Hydrol 577:123989. https://doi.org/10.1016/j.jhydrol.2019.123989
Madani K, Read L, Shalikarian L (2014a) Voting under uncertainty: a stochastic framework for analyzing group decision making problems. Water Resour Manag 28(7):1839–1856. https://doi.org/10.1007/s11269-014-0556-8
Madani K, Zarezadeh M, Morid S (2014b) A new framework for resolving conflicts over transboundary rivers using bankruptcy methods. Hydrol Earth Syst Sci 18(8):3055–3068. https://doi.org/10.5194/hess-18-3055-2014
Mianabadi H, Mostert E, Zarghami M et al (2014) A new bankruptcy method for conflict resolution in water resources allocation. J Environ Manag. https://doi.org/10.1016/j.jenvman.2014.05.018
Mianabadi H, Mostert E, Pande S et al (2015) Weighted bankruptcy rules and transboundary water resources allocation. Water Resour Manag 29(7):2303–2321. https://doi.org/10.1007/s11269-015-0942-x
Mueller Schmied H, Eisner S, Franz D et al (2014) Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol Earth Syst Sci 18(9):3511–3538. https://doi.org/10.5194/hess-18-3511-2014
O’Neill B (1982) A problem of rights arbitration from the talmud. Math Soc Sci 2(4):345–371. https://doi.org/10.1016/0165-4896(82)90029-4
Read L, Madani K, Inanloo B (2014) Optimality versus stability in water resource allocation. J Environ Manag 133:343–354
Salman SM (2007) The Helsinki rules, the UN watercourses convention and the berlin rules: Perspectives on international water law. Water Resour Dev 23(4):625–640. https://doi.org/10.1080/07900620701488562
Sang X, Wang H, Wang J et al (2018) Water resources comprehensive allocation and simulation model WAS(I): Theory and development. Shuili Xuebao/J Hydraul Eng 49(12):1451–1459. https://doi.org/10.13243/j.cnki.slxb.20180507
Sechi GM, Zucca R (2015) Water resource allocation in critical scarcity conditions: a bankruptcy game approach. Water Resour Manag 29(2SI):541–555. https://doi.org/10.1007/s11269-014-0786-9
Srdjevic B (2007) Linking analytic hierarchy process and social choice methods to support group decision-making in water management. Decision Supp Syst 42(4):2261–2273. https://doi.org/10.1016/j.dss.2006.08.001
Thomson W (2003) Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: a survey. Math Soc Sci 45(3):249–297. https://doi.org/10.1016/S0165-4896(02)00070-7
Wang J, Sang X, Zhai Z et al (2014) An integrated model for simulating regional water resources based on total evapotranspiration control approach. Adv Meteorol 2014:1–10. https://doi.org/10.1155/2014/345671
Wang J, Song C, Reager JT et al (2018) Recent global decline in endorheic basin water storages. Nat Geosci 11(12):926–+. https://doi.org/10.1038/s41561-018-0265-7
WWAP (2020) The united nations world water development report 2020: Water and climate change
Yan Z, Zhou Z, Liu J et al (2020) Multiobjective optimal operation of reservoirs based on water supply, power generation, and river ecosystem with a new water resource allocation model. J Water Resour Plan Manag 146(12):05020024. https://doi.org/10.1061/(ASCE)WR.1943-5452.0001302
Yazdian M, Rakhshandehroo G, Nikoo MR et al (2021) Groundwater sustainability: Developing a non-cooperative optimal management scenario in shared groundwater resources under water bankruptcy conditions. J Environ Manag 292(112807). https://doi.org/10.1016/j.jenvman.2021.112807
Yong Z, Li J, Cai Y et al (2017) Equitable and reasonable freshwater allocation based on a multi-criteria decision making approach with hydrologically constrained bankruptcy rules. Ecol Indicators 73:203–213. https://doi.org/10.1016/j.ecolind.2016.08.049
Yu Y, Tang P, Zhao J et al (2019) Evolutionary cooperation in transboundary river basins. Water Resour Res 55(11):9977–9994. https://doi.org/10.1029/2019WR025608
Yuan L, He W, Degefu DM et al (2017) Water allocation model in the lancing-mekong river basin based on bankruptcy theory and bargaining game. World Environ Water Congr 2017:78–92. https://doi.org/10.1061/9780784480595.008
Zhai Zl, Sang Xf, Chen J et al (2017) The total control of water supply and water consumption in Tianjin city based on was model. The 3rd International Conference on Green Materials and Environmental Engineering (GMEE), p. 56–60
Zolfagharipoor MA, Ahmadi A (2016) A decision-making framework for river water quality management under uncertainty: Application of social choice rules. J Environ Manag 183(1):152–163. https://doi.org/10.1016/j.jenvman.2016.07.094
Acknowledgements
This study was supported by the National Key Research and Development Program of China (2021YFC3200200), China Three Gorges Corporation Research Project (Contract No: 202103044), and the Scientific Research Projects of IWHR (WR0145B062021, WR0145B042021). The authors wish to express their gratitude for the support.
Funding
This study was supported by the National Key Research and Development Program of China (2021YFC3200200), China Three Gorges Corporation Research Project (Contract No: 202103044), and the Scientific Research Projects of IWHR (WR0145B062021, WR0145B042021).
Author information
Authors and Affiliations
Contributions
Y.Z. developed the models and methods, analyzed the data, and drafted the manuscript; X.S. guided and supervised the whole process; S.Z. collected the data; Z.L., S.Z. and P.L. discussed the idea and revised the manuscript; and all authors read and approved the manuscript.
Corresponding author
Ethics declarations
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Conflict of Interest
The authors have no relevant financial or non-financial interests to disclose.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zheng, Y., Sang, X., Liu, Z. et al. Water Allocation Management Under Scarcity: a Bankruptcy Approach. Water Resour Manage 36, 2891–2912 (2022). https://doi.org/10.1007/s11269-022-03098-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-022-03098-0