A Cox Process with State-Dependent Exponential Pulses to Model Rainfall

Abstract

A point process model based on a class of Cox processes is developed to analyse precipitation data at a point location. The model is constructed using state-dependent exponential pulses that are governed by an unobserved underlying Markov chain. The mathematical formulation of the model where both the arrival rate of the rain cells and the initial pulse depth are determined by the Markov chain is presented. Second-order properties of the rainfall depth process are derived and utilised in model assessment. A method of moment estimation is employed in model fitting. The proposed model is used to analyse 69 years of sub-hourly rainfall data from Germany and 15 years of English rainfall data. The results of the analysis using variants of the proposed model with fixed pulse lifetime and variable pulse duration are presented. The performance of the proposed model, in reproducing second-moment characteristics of the rainfall, is compared with that of two stochastic models where one has exponential pulses and the other has rectangular pulses. The proposed model is found to capture most of the empirical rainfall properties well and outperform the two alternative models considered in our analysis.

Introduction

Rainfall is the main input to hydrological systems. Access to rainfall data is therefore essential to an understanding of how a hydrological catchment behaves. Available rainfall data sets are however often not long enough for the application in question. The lack of available data might mean that it is impossible to assess catchment response to a sufficiently wide range of rainfall events, or lead to poor estimates of the probability of high or low flows. Hydrological studies, flood and drought design will thus all benefit from the availability of a stochastic rainfall model that is able to generate long series of rainfall at scales such as one hour.

There are many approaches to modelling precipitation as a stochastic process. Among them, the following classes can be distinguished:

• statistical models which may for instance involve the use of a standard distribution to represent the rainfall depth, with Markov chain occurrences (Kannan and Farook 2015), of a Generalised Linear Model to relate rainfall with climatological drivers (Chandler and Wheater 2002), or of (S)ARIMA models (Dabral and Murry 2017); alternatively, the task is to specify both a marginal distribution and a correlation structure (see Papalexiou 2018);

• models in which the scaling, i.e. scale-independent features of rainfall depths over ranges of temporal scales are modelled explicitly (Lovejoy and Schertzer 2013);

• mechanistic models in which the scale-dependent features of the rainfall time-series are modelled explicitly (Onof et al. 2000).

Models in the last category involve representations of the clustering of small contributions by rain cells to the total depth, in which the clustering of these cells inside storms is either modelled explicitly (Poisson-cluster models) or arises from having the rates of arrival of cells governed by a Markov process (Doubly stochastic or Cox models). The first approach is more prominent in the literature as the initial seminal paper by Rodriguez-Iturbe et al. (1987) triggered a series of publications over the past 30 years in which the models they presented were further developed and tested with a growing range of types of rainfall. These typically focused on the use of one of two types of clustering processes for the underlying continuous rainfall process: the Bartlett-Lewis and the Neyman-Scott processes. In the first, cell arrivals follow the storm arrival in a secondary Poisson process which is truncated by a random variable representing the duration of storm activity. In the second, two random variables are specified: the delay between storm and cell arrival and the number of cells per storm. For reviews of the first period of these developments, see Onof et al. (2000). For more recent papers in this area, see Kilsby et al. (2007), Kaczmarska et al. (2014), Onof and Wang (2020), Kim and Onof (2020), Aryal and Jones (2020).

The second, i.e. doubly stochastic approach has been developed in parallel and benefited from consistent improvements over the past 10 years. Ramesh et al. (2012) employed a class of doubly stochastic Poisson point processes (DSPP), rather than Poisson cluster processes, as the driving point process in their stochastic models. Thayakaran and Ramesh (2013) extended this class of models to a multi-site model. Thayakaran and Ramesh (2017) explored the use of instantaneous pulses with these doubly stochastic models. Garthwaite and Ramesh (2018) utilised this class of models, incorporating reanalysis climatological data, to model winter season rainfall. These models were further developed by attaching an exponentially decaying pulse to each point of such a point process with the focus on reproducing the properties of fine-scale rainfall (Ramesh et al. 2017).

The aim of this paper is to pursue this research programme of exploration of the potential of DSPP models in modelling observed rainfall. The appeal of this modelling approach is that it explicitly models an underlying non-observed state of the rainfall process which represents the atmospheric drivers of the rainfall generation mechanism. Here, we extend this class of Cox process models with exponentially decaying pulses by allowing the distribution of the initial pulse depth to be dependent on the state of the underlying Markov chain. This innovation we present in this paper makes an important contribution to the realism of such models in that it imparts greater physical realism to them. This is because the pulse depth distribution is now dependent upon the underlying atmospheric state. This new model is used to describe the probabilistic structure of the rainfall at a single rain-gauge. The proposed model is applied to a set of sub-hourly rainfall data from Bracknell in England, obtained from the U.K. Meteorological Office, and also to a set of rainfall data from Bochum, Germany.

The mathematical formulation of the proposed Cox process model with state-dependent exponential pulses is described in Sect. 2. Second-moment characteristics of the rainfall intensity are studied in Sect. 3. Mathematical expressions for the aggregated rainfall processes are also derived in Sect. 3. Parameter estimation is discussed in Sect. 4. A case study, which employs two different versions of the model, using 15 years of English rainfall data and 69 years of German rainfall data is presented in Sect. 5: the performance of the proposed model is thereby compared with that of a doubly stochastic rectangular pulse model and another exponential pulse model. Conclusions are summarised in Sect. 6.

Exponential Pulse Model with State-Dependent Initial Pulse Depth

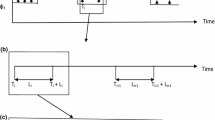
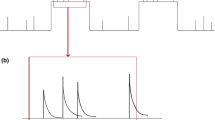
Let $\left\{N(t)\right\}$ be a stationary Cox process, evolving in time, representing the arrival pattern of rain cells at a location. Suppose that the arrival rate of the process is governed by an underlying two-state continuous time Markov chain where state one represents the low intensity rain spell and state two the high intensity one. The arrival rates of rain cells in the two states are denoted by $\phi _1$ and $\phi_2$ respectively, whereas the transition rates of the Markov chain between the two states are denoted by $\lambda \, (1 \rightarrow 2)$ and $\mu \, (2 \rightarrow 1)$. Each cell of the point process $\left\{N(t)\right\}$ has a rainfall pulse of random initial ‘depth’ X and the pulse depth decays exponentially with time at a constant rate $\beta$. The initial depth of the rain pulse depends on the state of the Markov chain at the pulse origin. The state-dependent distributions of the initial pulse depth in the two states are left unspecified. The mean initial depths of rain pulses are $\mu _{X_1}$ and $\mu _{X_2}$ in states one and two, respectively. All the active pulses terminate after a fixed duration d. The pulses are taken as mutually independent, as well as independent of the point process $\left\{N(t)\right\}$.

We define a random variable $X_{t-u}(u)$ as the rainfall depth of the pulse originating at time $(t-u)$, measured at time t. $X_{t-u}(u)$ is given by the following equation:

$$\begin{aligned} X_{t-u}(u) = {\left\{ \begin{array}{ll} X_1e^{-\beta u} &{} \text {if Markov chain is in State 1 at} \;(t-u) \; \text {and} \;u \le d \\ X_2e^{-\beta u} &{} \text {if Markov chain is in State 2 at} \;(t-u) \; \text {and} \;u\le d \\ 0 &{} \text {if} \;u > d \end{array}\right. } \end{aligned}$$

(1)

where $X_1$ and $X_2$ are the initial amplitudes of pulses in States 1 and 2 respectively. The rainfall intensity Y(t) at time t is the sum of all active pulses at time t and so can be written as

$$\begin{aligned} Y(t)= \sum _{t_i\in [t-d,t]} X_{t_i}(t-t_i)= \int _{u=0}^{d} X_{t-u}(u) dN(t-u). \end{aligned}$$

(2)

A schematic description of the model is displayed in Fig. 1.

Fig. 1

Diagrammatic representation of state-dependent initial depth exponential pulse model with a fixed pulse duration d

Second-Order Properties of the Processes

To study the second-order properties, let $\pi =[\pi _1,\pi _2]$ be the stationary distribution of the underlying Markov chain which is obtained by solving $\pi$ Q= $0_{1\times 2}$ under the constraint $\pi _1$ + $\pi _2$ =1, where Q is the generator matrix, and is given by $\pi _1$= $\frac{\mu }{\lambda +\mu }$ and $\pi _2$= $\frac{\lambda }{\lambda +\mu }.$ The mean initial depth of a pulse is obtained by conditioning on the state of the underlying Markov chain at the origin of the pulse and it can be written as $E(X)=\mu _X=\pi _1\mu _{X_1}+\pi _2\mu _{X_2}.$

Second-Order Properties of the Intensity Process

We shall first study the second-order moment properties of the rainfall intensity process Y(t) recognising that they are related to the properties of the point process $\left\{N(t)\right\}$. The mean intensity of the point process $\left\{N(t)\right\}$ is given by $m=\pi _1\phi _1+\pi _2\phi _2=\frac{\lambda \phi _2+\mu \phi _1}{(\lambda +\mu )}$. Hence, the mean of the rainfall intensity process Y(t) is obtained by taking expectations on both sides of the Eq. (2) and is given as:

$$\begin{aligned} E[Y(t)]&= \int _{0}^\infty E\left\{X e^{-\beta u } \right\} \quad dN(t-u) \nonumber \\&=\int _{0}^d E\left\{X\right\} e^{-\beta u } \quad dN(t-u)\nonumber \\&=\left( \pi _1 \mu _{X_1} + \pi _2 \mu _{X_2} \right) \Big (\frac{1-[e^{-\beta d}]}{\beta }\Big ) \Big (\frac{\lambda \phi _2+\mu \phi _1}{(\lambda +\mu )}\Big ) \end{aligned}$$

(3)

The autocovariance of the rainfall intensity process Y(t) at lag $\tau$ is defined by:

$$\begin{aligned} C_Y(\tau )&= \mathrm {Cov} [Y(t),Y(t+\tau )]\nonumber \\&= \int _{0}^{\infty }\int _{0}^{\infty }E\left\{X_{(t-u)}(u)X_{(t+\tau -v)}(v)\right\} \mathrm {Cov}\left\{dN(t-u),dN(t+\tau -v)\right\}, \end{aligned}$$

(4)

where Cov $\left\{dN(t),dN(t+u)\right\}$ is the covariance density of the point process $\left\{N(t)\right\}$. Ramesh (1998) showed that

$$\begin{aligned} \mathrm {Cov}\left\{dN(t),dN(t+u)\right\}= m \delta (u)+Ae^{-(\lambda +\mu )u} \end{aligned}$$

where $\delta (.)$ is the Dirac delta function and A is a constant given by $A=\frac{\lambda \mu (\phi _1-\phi _2)^2}{(\lambda +\mu )}.$ Using this in Eq. (4), we obtain the expression for the covariance of the rainfall intensity process Y(t) as follows:

$$\begin{aligned} C_Y(\tau )&= \int _{0}^d\int _{0}^d E[X_{t-u}(u)\quad X_{t+\tau -v}(v)]\quad \left\{m\delta (u+\tau -v)+Ae^{-(\lambda +\mu )(\tau +u-v)} \right\}\quad du \; dv \nonumber \\&=mE[X^2]\int _{0}^d e^{-\beta (\tau +u)}du+A\int _{0}^d\int _{0}^dE(X)e^{-\beta u } E(X)e^{(-\beta v)}\left\{ e^{-(\lambda +\mu )(\tau +u-v)}\right\}\quad du\; dv \nonumber \end{aligned}$$

By completing the two integrals, we obtain:

$$\begin{aligned} C_Y(\tau ) = \frac{\left\{mE[X^2]e^{-\beta \tau } [1-e^{-\beta d}] \right\}}{\beta }+ \Big [ \frac{A\mu _X^2 e^{-\tau (\lambda +\mu )}[1-e^{-d(\beta -\lambda -\mu )}-e^{-d(\beta +\lambda +\mu )}+e^{-2\beta d}]}{(\beta +[\lambda +\mu ])(\beta -[\lambda +\mu ])}\Big ] \end{aligned}$$

(5)

It follows that, by conditioning on the state of the underlying Markov chain at the origin of a pulse,

$$\begin{aligned} E[X^2]=[\pi _1E(X_1^2)+\pi _2E(X_2^2)]\quad \mathrm {and} \quad \mu _X^2=[E(X)]^2=[\pi _1\mu _{X_1}+\pi _2\mu _{X_2}]^2 \end{aligned}$$

Hence, by substituting these expressions in Eq. (5), we get

$$\begin{aligned} \mathrm {C}_Y(\tau )&= K_1 (1-e^{-\beta d})e^{-\beta \tau } +K_2 (1-e^{-(\lambda +\mu ) d}) e^{-(\lambda +\mu )\tau } \end{aligned}$$

(6)

where,

$$\begin{aligned} K_1&= \frac{m[\pi _1E(X_1^2)+\pi _2E(X_2^2)](1-e^{-\beta d})}{\beta } \nonumber \\ K_2&=\frac{\left\{A [\pi _1\mu _{X_1}+\pi _2\mu _{X_2}]^2 [1-e^{-d(\beta -\lambda -\mu )}-e^{-d(\beta +\lambda +\mu )}+e^{-2\beta d}] \right\}}{(\beta ^2 - (\lambda +\mu )^2)} \nonumber \end{aligned}$$

The variance of the rainfall intensity process is obtained by setting $\tau$ = 0 in Eq. (6), and is given by:

$$\begin{aligned} \mathrm {Var}[Y(t)]&=\frac{\left\{m[\pi _1E(X_1^2)+\pi _2E(X_2^2)](1-e^{-\beta d}) \right\}}{\beta } \nonumber \\&+\frac{\left\{A [\pi _1\mu _{X_1}+\pi _2\mu _{X_2}]^2 [1-e^{-d(\beta -\lambda -\mu )}-e^{-d(\beta +\lambda +\mu )}+e^{-2\beta d}] \right\}}{(\beta ^2 - (\lambda +\mu )^2)} \end{aligned}$$

(7)

Second-Order Properties of the Aggregated Process

Rainfall is normally recorded in the form of cumulative amounts over discrete time intervals of a constant width such as hourly or daily rainfall. In order to study the properties of the aggregated rainfall totals in disjoint intervals of length h, we define $Y_i^{(h)}$ for $i= 1,2,\cdots ,$ as

$$\begin{aligned} Y_i^{(h)}=\int _{(i-1)h}^{(ih)} Y(u) du. \end{aligned}$$

The second-moment properties of the aggregated rainfall can be obtained by using the following general expressions given by Rodriguez-Iturbe et al. (1987)

$$\begin{aligned} E\left\{Y_i^{(h)}\right\}&=hE\left\{Y(t)\right\}\end{aligned}$$

(8)

$$\begin{aligned} \mathrm {Var}{Y_i^{(h)}}&= 2 \int _{0}^h (h-u) C_Y(u)\quad du\end{aligned}$$

(9)

$$\begin{aligned} \mathrm {Cov}\left\{Y_i^{(h)}, Y_{i+k}^{(h)} \right\}&= \int _{-h}^h C_Y(kh+u) (h-|u|)\quad du \end{aligned}$$

(10)

In addition, we also make use of the following two integrals in our derivation

$$\begin{aligned} \int _{0}^h (h-u)e^{-cu} = \frac{h}{c}-\frac{1}{c^2}+\frac{e^{-ch}}{c^2} \quad \mathrm {and} \quad \int _{-h}^0 (h-u)e^{-cu} =\frac{-h}{c}-\frac{1}{c^2}+\frac{e^{ch}}{c^2}. \end{aligned}$$

Using the above results and substituting the equations for $E\left\{Y(t)\right\}$ and $C_Y (\tau )$ given by Eqs. (3) and (6) into Eqs. (8)−(10), we obtain the following expressions for the mean, variance and autocovariance of the aggregated rainfall process for our model as:

$$\begin{aligned} E\left\{Y_i^{(h)}\right\}&=h[\pi _1 \mu _{X1} + \pi _2 \mu _{X2} ] \Big (\frac{1-e^{-\beta d}}{\beta }\Big ) \Big (\frac{\lambda \phi _2+\mu \phi _1}{(\lambda +\mu )}\Big )\end{aligned}$$

(11)

$$\begin{aligned} \mathrm {Var}(Y_i^{(h)})&= 2K_1\left[ \frac{h}{\beta }-\frac{1}{\beta ^2}+\frac{e^{-\beta h}}{\beta ^2} \right] + 2 K_2\left[ \frac{h}{(\lambda +\mu )}-\frac{1}{(\lambda +\mu )^2}+\frac{e^{-h(\lambda +\mu )}}{(\lambda +\mu )^2} \right] \end{aligned}$$

(12)

$$\begin{aligned} \mathrm {Cov}\left\{Y_i^{(h)}, Y_{i+k}^{(h)} \right\}&=K_1 \Big [\frac{1-2e^{-\beta h} +e^{-2\beta h}}{\beta ^2}\Big ] e^{-\beta (k-1)h} \nonumber \\&\;+ K_2 \Big [\frac{1-2e^{-(\lambda +\mu )h}+e^{-2(\lambda +\mu )h}}{(\lambda +\mu )^2}\Big ] e^{-(\lambda +\mu )(k-1)h} \end{aligned}$$

(13)

Note here that the derivation of these equations does not assume any specific distribution for the initial pulse depth X. However, in the data analysis section below we assume an exponential distribution for X, although other distributions can be used.

Estimation of Model Parameters

In the absence of a suitable likelihood function in a closed form, stochastic models are usually fitted with the generalised method of moments. A set of properties are chosen so as to minimise some measure of discrepancy between the theoretical and empirical estimates of the chosen properties. Let y be a vector of observations and $\theta$=( $\theta _{1}$, $\theta _2$,..., $\theta _p)$ be a vector of unknown parameters in the model. Let $T(y)=(T_1(y), \cdots ,T_k(y))$ be the vector of summary empirical statistics calculated from the observations and $E_\theta (T(y))= \zeta (\theta )=( \zeta _1(\theta ),\cdots , \zeta _k(\theta ))$ be the theoretical expected value of the chosen summary statistics according to the model. Denote the measure of disagreement between T and $\zeta$ by

$$\begin{aligned} S(\theta \mid y)= \sum _{i=1}^{k} w_i [T_i (y)-\zeta _i (\theta )]^2 \end{aligned}$$

(14)

where $w_i$ is the weight assigned to the $i^{\text {th}}$ term in the summation and $\zeta _i(\theta )$ is the expected value of the $i^{\text {th}}$ summary statistics. The method of moment estimates are obtained by minimising $S(\theta \mid y)$ over $\theta$.

Objective Functions

The models we considered in this paper have either seven or eight parameters, depending on whether the pulse duration is taken as a constant or variable. We employ the Method of Moment (MoM) estimation technique to estimate the model parameters and use the mean ($\mu$), standard deviation ($\sigma$) and lag-1 autocorrelation ($\rho$) at different time-scales. There are several choices for the objective function to be used in MoM estimation including the generalised method of moment technique suggested by Jesus and Chandler (2011). Another useful objective function utilised by Cowpertwait et al. (2007) is given as

$$\begin{aligned} \sum _{h} \left( \left( 1-\frac{\hat{\mu }(h)}{\mu (h)}\right) ^2+\left( 1-\frac{\mu (h)}{\hat{\mu }(h)}\right) ^2+\left( 1-\frac{\hat{\sigma }(h)}{\sigma (h)}\right) ^2+\left( 1-\frac{\sigma (h)}{\hat{\sigma }(h)}\right) ^2+\left( 1-\frac{\hat{\rho }(h)}{\rho (h)}\right) ^2+\left( 1-\frac{\rho (h)}{\hat{\rho }(h)}\right) ^2\right) \end{aligned}$$

(15)

This function can also be modified to incorporate a weighted sum of squares, where $w_{ih}$ is the weight assigned to the $i^{th}$ statistics at time-scale h:

$$\begin{aligned}&\sum _{h} \left( w_{1h}\left[ \left( 1-\frac{\hat{\mu }(h)}{\mu (h)}\right) ^2+\left( 1-\frac{\mu (h)}{\hat{\mu }(h)}\right) ^2 \right] +w_{2h}\left[ \left( 1-\frac{\hat{\sigma }(h)}{\sigma (h)}\right) ^2+\left( 1-\frac{\sigma (h)}{\hat{\sigma }(h)}\right) ^2\right] \right. \nonumber \\&+ \left. w_{3h}\left[ \left( 1-\frac{\hat{\rho }(h)}{\rho (h)}\right) ^2+\left( 1-\frac{\rho (h)}{\hat{\rho }(h)}\right) ^2\right] \right) \end{aligned}$$

(16)

Optimisation

We use the objective function given by either Eq. (15) or (16) to estimate model parameters. The objective function (16) works better for large data sets and is therefore used for the German rainfall data. Numerical minimisation of the objective function is performed using R optimisation routines (R-Core-Team 2017) that uses function evaluations as well as derivatives. The approach we used was to employ an initial search algorithm that uses function evaluations only (Nelder-Mead downhill simplex method) to find a promising region of optimal parameter values in the parameter space. A derivative based algorithm is then utilised to find refined estimates.

Data Analysis

The model developed in Sect. 2 has been applied to two different data sets, one from Bracknell in England and the other from Bochum in Germany. The Bracknell data set was collected over a period of 15 years, in the form of rainfall bucket tip times, whereas the Bochum data set was collected as five minute rainfall depths over a period of 69 years. We explored two different versions of the model proposed in Sect. 2. The first one assumed that the lifetime of the rain pulses terminates after a fixed duration d and the second one extended this model by taking the pulse duration d as a random variable.

Analysis of Bracknell Data

We begin our analysis with the fixed pulse duration model applied to the Bracknell data. Previous studies suggest that $d=1$ is sufficient to capture the properties of rainfall well and we shall use this value in our analysis. In addition, we take the initial pulse depth X at the pulse origins as independent random variables with an exponential distribution with parameter $\theta _1$ at State 1 and $\theta _2$ at State 2. Our model then has seven parameters per month and we estimate them by the method of moments approach using the objective function given in Eq. (15). The estimates of the model parameters, when this model is applied to the Bracknell data, are given in Table A1 (See Supplementary Material for Table A1). The time-scales used in fitting were $h=20$ minutes for the mean and $h=10, 30, 60$ minutes for the standard deviation and lag-1 correlation. The estimates show that the rainfall bursts have high arrival rates ($\phi _2$) in State 2 with shorter sojourn times ($1/\mu$) and low arrivals ($\phi _1$) with long sojourn times ($1/\lambda$) in State 1.

Our model performance is assessed by comparing the fitted values of the theoretical properties, calculated using the estimated parameters, with the corresponding empirical values. The comparison was made at both sub-hourly and sub-daily time-scales, including those that are not used in fitting. In addition, simulation bands using 1000 simulations from the fitted model were calculated and displayed with observed (empirical) and fitted (theoretical) values.

For all the plots in this section, the black line represents the empirical values, the blue line shows the fitted values of our proposed state-dependent exponentially decaying initial pulse model M2, the red lines show the simulation bands. We compare the results of the proposed model (M2) with that of the model which has a common initial pulse distribution in both states (M1). The brown dashed lines are for model M1: they are included in the plots for comparison. Figure A1 shows that the empirical and fitted means of the aggregated rainfall at $h=1$ hour are in excellent agreement and hence the mean rainfall has been reproduced well by the fitted model (see Supplementary Material for Fig. A1). The same is true at all the other time-scales, as the mean is simply scaled by a factor of h.

The empirical and fitted values of the standard deviation of the accumulated rainfall at several time-scales ($h=1/6, 1, 6$ hours) are displayed in the left-hand panels of Fig. A2, along with simulation bands (see Supplementary Material for Fig. A2). Here again, both observed and fitted curves are in excellent agreement, at all time-scales, and the alignment between the observed and fitted values of our proposed model M2 is better than that of the reference model M1 which has a fitted value outside the simulation bands for the month May. The empirical and fitted values of the lag-1 autocorrelation of the accumulated rainfall are displayed in the right-hand panels of Fig. A2, along with simulation bands. Both observed and fitted curves are in excellent agreement at finer time-scales. Although there are some differences between the observed and fitted curves at coarser time-scales, they are both well within the simulation bands. Here again the model M2 provides a better fit.

The observed and fitted values of the coefficient of variation of the aggregated rainfall are in good agreement at all time-scales in the left-hand panels of Fig. A3, including those that are not used in fitting (See Supplementary Material for Fig. A3). Once again it is noticeable that the proposed model M2 has better alignment with empirical values than the model M1. The right-hand panels of Fig. A3 display the observed values of the proportion of dry periods together with simulation bands from the fitted model M2 at time-scales $h=1/12, 1/6, 1/3$ hours. The model appears to reproduce these reasonably well and capture their pattern across the year quite well at finer time-scales, but not at coarser time-scales. Our model tends to overestimate the proportion of dry periods at coarser time-scales. However, these statistics are not used in fitting and hard to reproduce at all values of h, as they depend more on the scale of measurement.

To compare the performance of the two models (M2 and M1) numerically, we calculated the root mean square error (RMSE) of the three statistics used in fitting. Their mean square error is calculated as the squared difference between the empirical and fitted values of the statistics averaged over all eleven time-scales considered in our analysis, from h=1/12 to $h=24$, separately for each month. The smaller the values of the RMSE, the better the model fit, as it shows closer agreement between the observed and fitted values. Table A2 shows the values of the root mean square error of the three statistics mean, standard deviation and autocorrelation (see Supplementary Material for Table A2). It is clear from the Table that the RMSE values of the model M2 are mostly smaller than those of M1, which provides evidence of the fact that M2 outperforms M1.

Analysis of Bochum Data with Fixed Pulse Duration Model

Here, we use our state-dependent initial pulse model with the fixed pulse duration to analyse the Bochum rainfall data over a 69 year period. We start our analysis by taking the pulse duration as $d=1$ and assume that the initial pulse depths follow exponential distributions with mean $1/\theta _1$ and $1/\theta _2$ in States 1 and 2, respectively. This model was fitted to the data using the weighted objective function given in Eq. (16) separately for each month, to obtain the parameter estimates and they are given in Table A3 (see Supplementary Material for Table A3). The weights applied to the statistics in the objective function were calculated as the reciprocal variance of the yearly statistics at each time-scale over the 69 years. The time-scales used in fitting were $h=60$ minutes for the mean and $h=5, 20, 60$ minutes for both the standard deviation and autocorrelation, as well as $h=12$ hour for autocorrelation.

The estimates show that the overall pattern of the rainfall characteristics is similar to that of the Bracknell data, suggesting the two regions have similar rainfall patterns. The Bochum rainfall bursts have slightly smaller arrival rates ($\phi _1, \; \phi _2$) but longer sojourn times ($1/\lambda , \;1/\mu$) in both states when compared with those of Bracknell data. In addition, both states have larger mean for initial pulse depth ($1/\theta _1$, $1/\theta _2$) for the Bochum data. This suggests that Bochum experiences fewer rainfall bursts but with larger initial pulse depth than Bracknell. Another point worth noting is that the estimates of the parameter $\beta$ for Bochum data are smaller than those for Bracknell, which suggests that the rain pulses take longer to deposit the rain. Estimates of $\beta$ show that, for each of the 12 months, the rain pulses deposit 95% of their rain within 30 minutes, and 99% within 50 minutes from their pulse origin.

The plot for the observed and fitted mean rainfall at time-scale $h=1$ is displayed in Fig. A4 (see Supplementary Material for Fig. A4). There is close agreement between the fitted and empirical values at $h=1$ hour and also at all other time-scales. The left-hand panels of Fig. 2 show the empirical and fitted values of the standard deviation of the accumulated rainfall at time-scales $h=1/6, 1, 6$ hours along with their simulation bands. Here again both observed and fitted curves are in near perfect agreement at all time-scales, including those that are not used in fitting. The same can be said about the empirical and fitted values of the lag-1 autocorrelation of the accumulated rainfall displayed in the right-hand panels of Fig. 2.

The left-hand panels of Fig. 3 show the empirical values of the skewness coefficient for the accumulated rainfall at time-scales $h=1/6, 1, 6$ hours along with the simulation bands from the fitted model. The fitted model clearly underestimates the skewness at sub-hourly time-scales but does reasonably well at coarser time-scales. The right-hand panels of Fig. 3 display the empirical values of the proportion of dry periods together with a simulation band from the fitted model M2 at time-scales $h=1/12, 1/6, 1/3$ hours. The model appears to reproduce the proportion of dry periods reasonably well and capture its pattern across the year quite well at these sub-hourly time-scales, but not at coarser time-scales.

Fig. 2

Observed (black) and fitted (blue) values of the standard deviation (left-hand panels) and autocorrrelation (right-hand panels) of the aggregated rainfall at h=1/6, 1, 6 hours for the model M2 along with simulation bands (red) for Bochum data

Fig. 3

Observed (black) values of the skewness (left-hand panels) coefficient of the aggregated rainfall for the model M2 along with simulation bands (red) for Bochum data. The right-hand panels show the observed values (black) of the proportion of dry periods with simulation bands (red) from the fitted model M2

Analysis of Bochum Data with Variable Pulse Duration Model

In this section, we extend our model to allow the pulse lifetime d to vary rather than taking a fixed value. This can be done in different ways and one approach is to take the pulse lifetime as a random variable with a specified distribution. Another approach is to take d as a parameter of the model and try to estimate it along with other parameters and we employ this second approach in this paper. When d is taken as a parameter, the expressions for mean, variance and autocovariance given in Eqs. (11), (12) and (13) are still valid and we treat them as functions of one additional parameter. The eight model parameters $\lambda ,\mu ,\phi _1,\phi _2,\beta ,\theta _1,\theta _2 \; \text {and}\; d$ are estimated by employing the weighted objective function (16) and using the statistics mean ($\mu$), variance ($\sigma$) and autocorrelation ($\rho$) over the same combination of time-scales as those used earlier for the fixed d model in Sect. 5.2. The estimated model parameters are given in Table 1.

Table 1 Parameter estimates for the state-dependent initial pulse depth model with variable pulse lifetime for Bochum data

The parameter estimates have similar patterns to those of the earlier model with fixed d and the mean sojourn times $1/\mu$ of the State 2 are shorter in summer months than those of the winter months. The values of overall $\hat{\mu }_X$ are again larger for summer months, showing higher initial rainfall intensity for the pulses, when compared with the winter months. The parameter estimates $\hat{\beta }$ are similar to those of the fixed d model used earlier. The estimated values of d suggest that the average duration of the pulse lifetime for Bochum is between 0.58 and 0.89 hours.

Fig. 4

Observed (black) and fitted (blue) values of the mean rainfall at h=1 hour time-scale for the state-dependent initial pulse depth model M2 with variable lifetime, along with simulation bands (red), for Bochum data. The dashed line (brown) is for the rectangular pulse model M0 discussed in Sect. 5.4

Fig. 5

Observed (black) and fitted (blue) values of the standard deviation (left-hand panels) and autocorrrelation (right-hand panels) of the aggregated rainfall at h=1/6, 1, 6 hours for the state-dependent initial depth model M2 with variable lifetime, along with simulation bands (red) for Bochum. The dashed line (brown) is for the rectangular pulse model M0 discussed in Sect. 5.4

Fig. 6

Left: Observed (black) values of the skewness coefficient for the aggregated rainfall at $h=1, 6, 24$ hours with simulation band (red) from the fitted model. Right: Observed (black) values of the proportion of dry period of the aggregated rainfall at $h=1/12, 1/6, 1/3$ for the state-dependent initial pulse depth model M2 with variable lifetime for the Bochum data

Figure 4 displays the observed and fitted means of the aggregated rainfall at $h=1$ and they are in perfect agreement which shows that the mean rainfall has been reproduced very well by the fitted model. The dashed line (brown) in Figs. 4 and 5 is for the fitted values of the model described in the next subsection, and is given here for comparison and will be discussed in Sect. 5.4. The empirical and fitted values of the standard deviation of the accumulated rainfall are given in the left-hand panels of Fig. 5 at sub-hourly and higher time-scales, along with simulation bands. Here again, both empirical and fitted values of our proposed model M2 are in excellent agreement at all time-scales, including those not used in fitting. The simulation bands suggest that the sampling distribution of the standard deviation is skewed at sub-hourly time-scales for the summer months but it gets better and less skewed at coarser time-scales. The observed and fitted values of the lag-1 autocorrelation of the aggregated rainfall for the state-dependant initial pulse model M2 are in very good agreement in the right-hand panels of Fig. 5 for all time-scales. Hence, the fitted model M2 performs well in reproducing the autocorrelations.

The empirical values of the skewness coefficient of the accumulated rainfall are given in the left-hand panels of Fig. 6, for hourly and higher time-scales, along with simulation bands. Our model vastly underestimates the skewness at sub-hourly time-scales but does reasonably well at coarser time-scales. The observed values of the proportion of dry periods are displayed in the right-hand panels of Fig. 6, together with simulation bands from the fitted model at sub-hourly time-scales. The model appears to reproduce these reasonably well and capture their pattern across the year quite well at $h=1/12,\; 1/6$ hours, but not at other time-scales. In general, our model overestimates the proportion of dry periods at coarser time-scales. These are, however, minor discrepancies given that these statistics are not used in the fitting, depend more on the scale of measurement and are affected by the occasional arrival of rain pulses in State 1.

Fig. 7

Ordered empirical annual maxima of the aggregated rainfall (red line) plotted against the reduced Gumbel variates for h=1/12, 1, 24 hours. Interval plots are based on annual maxima of 100 simulations from the fitted model M2. The return periods are specified at the foot of the plot above the x-axis

To study how well our model captures the extreme rainfall, we compare the annual extreme values of the observed rainfall data with those generated by the proposed model. Figure 7 shows the ordered empirical annual maximum rainfall (red solid lines) against the reduced Gumbel variate for $h=1/12, 1, 24$ hours along with the vertical interval plots showing the variability of the simulated ordered maxima from the fitted model. The mean of the 100 simulated ordered maxima for each plotting position is identified by the triangles in the interval plots . The return periods of the extreme rainfall are specified at the foot of the plot above the x-axis. At the five minute ($h=1/12$) time-scale, the model underestimates the extremes. As reported in previously published studies, see for example (Cowpertwait et al. 2007), the estimation of extreme values at sub-hourly time scales is a common problem for most stochastic point process models for rainfall and our results reveal the same. Despite the underestimation at the sub-hourly level, our model reproduces extremes well at the hourly time-scale, which is a notable improvement from earlier results (Ramesh et al. 2017), and the same goes for the daily time-scale.

Model Comparison

The variable pulse duration model described in Sect. 5.3 provided the best results for the Bochum data. To assess the performance of this model, we shall compare it with one of the existing doubly stochastic point process models for rainfall. The Bracknell data analysis in Sect. 5.2 compared the performance of the state-dependent initial pulse depth model M2 with that of the common initial pulse depth model M1. As there were no substantial differences in the results of the two models in that comparison despite some improvement, we now chose to compare the results of the state-dependent initial depth exponential pulse model M2 with that of a doubly stochastic rectangular pulse model (M0), described in Ramesh (1998), when both models are fitted to the Bochum data.

Figure 4 displays the empirical mean rainfall and the fitted values of the mean rainfall from the doubly stochastic rectangular pulse model (M0) as well as the state-dependent exponential pulse model (M2). The broken brown line shows the fitted values of this rectangular pulse model in Figs. 4 and 5 and the other lines of the plots are as described earlier in Sect. 5.3. Figure 4 shows that the mean rainfall has been reproduced better by our new model M2, especially for the summer months.

The left-hand panels of Fig. 5 compare the fitted values of the standard deviation of the accumulated rainfall from the two models with the empirical values at sub-hourly and coarser time-scales. The observed and fitted curves are in excellent agreement for the state-dependent exponential pulse model which clearly outperforms the rectangular pulse model at all time-scales in reproducing the standard deviation of the rainfall. The observed and fitted values of the lag-1 autocorrelation of the aggregated rainfall for the two models are compared in the right-hand panels of Fig. 5. They suggest that the rectangular pulse model vastly overestimates the autocorrelation at sub-hourly time-scales whereas, the state-dependent exponential pulse model provides a near perfect fit at these time-scales. The performance of the rectangular pulse model gets better at the hourly time-scale, although not as good as that of the exponential pulse model, but it gets worse again for coarser time-scales.

Here again, to compare the performance of the proposed state-dependent initial pulse depth model M2 with that of a rectangular pulse model M0 numerically, we calculated the root mean square error (RMSE) of the three statistics used in fitting. They are calculated as the square root of the squared difference between the empirical and fitted values of the statistics, averaged over all eleven time-scales considered in our analysis. Smaller values of the RMSE means closer alignment between the observed and fitted values. Table 2 shows the values of the root mean square error of the three statistics mean, standard deviation and autocorrelation for the two models M0 and M2 applied to the Bochum data. Results show that the RMSE values of the model M2 are smaller than those of M0 in almost every case, providing evidence to the fact that M2 outperforms M0.

Table 2 Root mean square error of the three statistics used in fitting for the models M0 and M2

Conclusions

This paper presented a class of Cox process models with state-dependent exponential pulses to describe the statistical properties of the accumulated rainfall totals. Mathematical expressions were derived for the second-order moment properties of the rainfall intensity and the aggregated rainfall processes. Our data analysis showed that the proposed model reproduced most of the second-moment properties well at various time-scales. We analysed two versions of the model, one with fixed duration for the pulse lifetime and the other with variable pulse lifetime. Both models performed well in reproducing the second-moment properties of rainfall but the variable-pulse-lifetime model showed some improvement, in terms of the alignment between the observed and fitted values of the properties studied.

Model performance was assessed by comparing the proposed state-dependent initial-pulse-depth model with either a common initial-pulse-depth model or a doubly-stochastic rectangular pulse model. The proposed model performed better in reproducing the rainfall properties in both cases. Possible future work could consider generalising the exponential decay of the initial pulse depth, by allowing two different rates of decay for the two states. This might introduce more variation in the rainfall duration. Another direction for future research would be to explore the extension of this model to a multi-site framework that will allow us to model rainfall data from multiple stations in a catchment area.