1 Introduction

There are two main factors that alter the hydrological cycle and cause changes in the spatio-temporal distribution of water availability in the catchment – direct human activities, i.e., land use change or channel modifications, and changes in climatic variables, i.e., temperature, evaporation and precipitation (Şen 2020; Dey and Mishra 2017).

If both climate and land use changes affect the catchment simultaneously, it may not be clear which of these two factors has a greater influence on the hydrological cycle (Ranzi et al. 2017). This knowledge is relevant in the context of adaptation to the environmental changes (Mohammed and Scholz 2017). Therefore, several attempts have been undertaken to separate and quantify both factors, to improve the ability to recognize environmental changes and to help plan the future management of water resources (Zuo et al. 2014). For instance, Dong et al. (2014) have reported that human activities are the major driver of runoff variation in the region of northwest China. For the same region, Chen et al. (2013) found that the contribution of climate shifts accounts for 90.5% of runoff change, while the land use change is responsible for only 9.5%. These two studies disclose difficulties in quantifying individual drivers of the hydrological cycle and show the need to improve our understanding of this complex interaction between human impact and climate change on water resources.

The relationship between runoff, climate change or direct human activities can be written as follows:

$$ \Delta Q={Q}_2-{Q}_1 $$
(1)
$$ \Delta Q={\varDelta Q}^H+\Delta {Q}^C $$
(2)

where:

ΔQ:

total change in runoff (mm),

Q2:

average runoff in the post-change period (mm),

Q1:

average runoff in the pre-change period (mm),

ΔQH:

land use or human contribution to the change of runoff (mm),

ΔQC:

climate change contribution to the change of runoff (mm),

This contribution of a specific change (land use or climate) can also be expressed in relation to the total change in runoff in the catchment as:

$$ \Delta {Q}_{\%}^H=\frac{\Delta {Q}^H}{\Delta Q}\times 100\% $$
(3)
$$ \Delta {Q}_{\%}^c=\frac{\Delta {Q}^H}{\Delta Q}\times 100\% $$
(4)

where:

\( \Delta {Q}_{\%}^H \) and \( \Delta {Q}_{\%}^C \) stand for the percentage contribution of land use and climate change to the change of runoff in a specific catchment.

The methods currently available to solve the set of Eqs. (1) and (2) can be divided into four major groups that are based on a) hydrological modelling, b) direct measurements in paired catchments, c) analytical methods and d) conceptual models (see Dey and Mishra 2017 for a review). All of these methods require long-term, high quality hydro-meteorological data. Moreover, different variants of equations describing the same process exist and therefore, authors are often left with an arbitrary decision in relation to the choice of the computation procedure. Consequently, the results of impact studies from different applications may often be difficult to compare, because they often focus on different spatial scales, from small watersheds to large basins. However, not all changes can be observed at all spatial scales (Xu 2000). For instance, small catchments are usually less affected by human activities, which can be better identified and localized than in large basins, where human activities may be multi-dimensional and not transparent (Krajewski et al. 2020). Yet, most of the previously developed methods to separate climate from human impact were tested with larger catchments. Thus, more impact studies in small catchments are needed to test the methods’ applicability to small catchments and to improve our knowledge relating to the human and climate interactions altering water resources.

Specifically, this study aims at: i) better understanding the coupled interactions between human activities, climate change and the aquatic ecosystem in a small Polish catchment (<100 km2) and ii) verifying available approaches to separate land use and climate change impacts on water resources in such a small catchment. The novelty of this study lies in the holistic approach of decomposing the effect of climate and land use changes on water resources in a small catchment with a very long observation record of hydro-climatic variables spanning 56 years. This combined with the history relating to land use changes, is an exception for such a small catchment. In this work, both the conceptual and analytical approach methods are applied, compared and discussed. The other two methods, i.e., hydrological modelling and paired catchments, are not within the scope of this paper. While methods using hydrological modelling are based on global climate models that are often inaccurate on a small catchment scale, the paired catchments method requires finding at least one sister-catchment free from anthropopressure. As such, a sister-catchment was not available for this study, therefore, this method could not be applied.

At the end of this paper, practical guidelines are given to the reader.

2 Methods

2.1 Study Set-up

The framework for assessing the direct human and climate impacts consists of the following steps; firstly, pre- and post-change periods are specified with the change point method. In addition, any changes in land use structure are identified. Secondly, hydro-meteorological variables are analysed for changes in time series. By comparing the characteristics over the pre- and post-change periods, it is then possible to estimate the impact of land use or climate changes on runoff. Note that if ∆QH and ΔQ were previously determined, the missing element, ∆QC may be calculated from Eq. (2). Thirdly, the contribution of land use and climate change to the runoff change may be delivered according to Eqs. (3) and (4). The following paragraphs describe the methodology in more detail.

2.2 Detection of Change Points

Change points (Page 1954) are abrupt variations in the time series data that split the observation into two or more sub-periods, having distinctive characteristics. These changes in time series can have different geneses and can originate from changes in observation locations, equipment, measurement techniques, environmental changes or direct human impact (Reeves et al. 2007), or from other unknown changes. However, detection of change points does not give any information as to the reason for an observed change. Thus, detection of change points should always be accompanied by analyses of the catchment history in relation to previous human activities (Kawahara and Sugiyama 2012).

With reference to streamflow time series, change points may represent a transition due to abrupt human activities, such as land use changes or the building of dams. Thus, the identification of change points (or periods of influence) in flow time series is important to separate impacts related to direct human activities from those linked with climate change (Dey and Mishra 2017). It is assumed that in the case of natural rivers, the variability in flow data before the change point is caused by climate change alone, whereas after the change point both the climate and human activities impact the water resources.

In this study, the function cpt.mean from the package “changepoint” (Killick 2016) of R programming language (R Core Team 2019) was used to identify single change points in the time series. This function finds changes in the mean of the observed time series, assuming the standard distribution of the data (Hinkley and Hinkley 1970). This function was applied to an observed series of runoff data over a long period of time, to better recognize climate change; it was also applied to the time series of temperature, evaporation and precipitation.

2.3 Conceptual Approach

2.3.1 Tomer and Schilling Framework

Tomer and Schilling (2009) proposed a method that enables an assessment of water and energy use by the ecosystem (catchment). To evaluate the changes, the energy and water excess must be determined:

$$ {E}_{ex}=\frac{PET- AE}{PET}, $$
(5)
$$ {P}_{ex}=\frac{P- AE}{P}, $$
(6)

where:

Eex:

energy excess, part of the available energy that is unused in the investigated period (−),

Pex:

water excess, part of the available water that is unused in the investigated period (−),

PET:

annual potential evapotranspiration (mm),

AE:

annual actual evapotranspiration (mm),

P:

annual precipitation (mm).

The shift of Eex and Pex over a long-term period indicates changes in the ecosystem. This method, however, only provides general insights as to whether the variation in runoff occurs due to climate change or land management practices (see Table S1 in Online Resources) without being able to quantify these changes.

2.3.2 Decomposition of the Budyko Curve

The Budyko hypothesis relies on the long-term water and energy balance of a catchment. Precipitation splits into runoff and evaporation, while the incoming solar radiation is equal to the sum of the heat of evaporation and the thermal radiation from the surface (Sposito 2017). Based on above relationships, Budyko (1974) assumed the ratio of annual evapotranspiration to annual precipitation (evaporation ratio) as being related to the ratio of annual potential evapotranspiration to annual precipitation (aridity index) and to catchment properties. An aridity index less than one means that the energy supply limits the evaporation.

A general form of the Budyko curve can be written as:

$$ \frac{AE}{P}=f\left(\frac{PET}{P}, catchment\ properties\right) $$
(7)

Equation (7) only represents a general relationship between the evaporation ratio and the aridity index. To be applied in practice, it requires defying specific formulations. Thus, different functional forms of the Budyko curve exist and are summarized in Table S2 in Online Resources.

To separate and quantify the extent of land use and climate change impacts on stream flows, a decomposition method, proposed by Wang and Hejazi (2011) is applied. This method assumes that without any land use changes or other direct human impacts, the evaporation ratio (PET/P) will also shift to a new region but will still follow the same Budyko curve, if the climate represented by the evaporation ratio (AE/P) moves to a drier or to a wetter region. However, any accompanying land use changes or direct human activities (e.g., irrigation) can additionally push the evaporation ratio in the vertical direction, i.e., by shifting it to a new position on a new curve lying outside the previous curve (Fig. 1). Under these assumptions, the effect of the land use change or direct human contribution to the streamflow can be calculated from the equation:

$$ \Delta {Q}^H={\mathrm{P}}_2\left(\frac{AE_2^{\prime }}{P_2}-\frac{AE_2}{P_2}\right) $$
(8)

where:

P2:

average annual precipitation in post-change period (mm),

\( {AE}_2^{\prime } \):

average annual evaporation in post-change period estimated according to the Budyko curve (mm),

AE2:

average annual evaporation in post-change period estimated according to the water balance equation (mm).

Fig. 1
figure 1

The concept of the Budyko curve decomposition, adapted from Wang and Hejazi (2011), and Dey and Mishra (2017)

Full size image

2.4 Analytical Approach

2.4.1 Climate Elasticity Method

The climate elasticity concept (Schaake 1990) is based on the computation of the ratio of a proportional change in runoff and a proportional change in climatic variables, i.e., precipitation and potential evapotranspiration. According to this method, the climate change contribution to the change of runoff is expressed as follows:

$$ \Delta {Q}^C=\left({\varepsilon}_P\frac{\Delta P}{\overline{P}}+{\varepsilon}_{PET}\frac{\Delta \mathrm{P} ET}{\overline{P}}\right)\overline{\mathrm{Q}} $$
(9)

where:

εP, εPET:

elasticity coefficients of streamflow with respect to precipitation and potential evapotranspiration,

\( \overline{\mathrm{P}} \):

long-term average annual precipitation (mm),

ΔP:

total change in precipitation (mm), estimated similarly to the total change in runoff in Eq. (1),

\( \overline{\mathrm{Q}} \):

long-term average annual runoff (mm),

ΔPET:

total change in potential evapotranspiration (mm), estimated similarly to the total change in runoff in Eq. (1).

The two elasticity coefficients εP and εPET are linked together as:

$$ {\varepsilon}_P+{\varepsilon}_{PET}=1 $$
(10)

To estimate εP, an analytical method using the Budyko hypothesis may be applied:

$$ {\varepsilon}_P=1+\frac{\frac{PET}{P}\times {f}^{\prime}\left(\frac{PET}{P}\right)}{1-f\left(\frac{PET}{P}\right)} $$
(11)

where:

\( f\left(\frac{PET}{P}\right) \):

functional form of the Budyko curve (Table S2 in Online Resources).

Having estimated εP, εPET can be computed from Eq. 10.

2.4.2 Hydrological Sensitivity Method

The hydrological sensitivity method describes a change in the mean annual runoff caused by a change in the mean annual precipitation and the mean annual potential evapotranspiration. In this method, the climate-induced change in runoff is determined by (Dey and Mishra 2017):

$$ \Delta {Q}^C=\beta \Delta P+\gamma \Delta PET $$
(12)

where:

β and γ are two runoff sensitivity coefficients to precipitation and to potential evapotranspiration (−). These two coefficients can be estimated from formulas established by Li et al. (2007) as well as Ma et al. (2008) that are based on the partial derivatives of the functional form of the Budyko curves (Table S3 in Online Resources).

3 Material

3.1 Study Catchment and Field Investigations

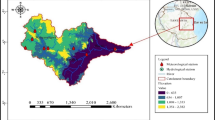
The study area is a small (82.4 km2, up to Płachty station, N:51°26′43.8″; E:21°27′35.6″) agricultural, lowland catchment of the Zagożdżonka River, a left tributary of the Vistula River, and is a research area of the Warsaw University of Life Sciences-SGGW (WULS-SGGW). The location of the catchment is given in Fig. S1 in Online Resources. The clear advantage of this catchment is a long-term record of hydro-meteorological variables dating back to the 1960s, which is exceptional for such a small catchment. Currently, there are two stream gauging stations located in this catchment: Płachty Stare (since 1962) and Czarna (since 1980), at which measurements of basic hydro-meteorological parameters are carried out continuously by the research team of WULS-SGGW. All measurements are carried out according to the standards recommended by the Polish Institute of Meteorology and Water Management (Barszczewska and Skąpski 2019).

The data records available for this study cover the period 1963–2018 and include: runoff, air temperature and precipitation.

3.2 Previous Study in the Zagożdżonka Catchment

The hydrological research in this catchment was initiated in 1962 to determine the water needs of the chemical plant in Pionki. Over time, the scope of the investigation has been expanded to water quality and sediment transport (Banasik et al. 2012; Hejduk and Hejduk 2019) and modelling of rainfall-runoff processes (Banasik et al. 2016; Krajewski et al. 2020).

Based on long-term analyses of the hydro-meteorological variables during the period 1963–2015, water resources were determined to decrease in this catchment. However, only recently did Krajewski et al. (2019) find significant decreasing trends for mean annual discharge (−2.5 dm3∙s−1∙year−1) and minimal annual discharge (−1.1 dm3∙s−1 year−1). Moreover, a significant increase in the mean annual air temperature was computed during the period 1951–2015 as 1.5 °C∙65 years−1. However, no trend could be established for the total annual precipitation and for the maximum summer daily rainfall amounts in that study.

3.3 Computation of Actual and Potential Evapotranspiration

Annual actual evapotranspiration is computed from long-term measurements of precipitations and runoff records according to the water balance equation (Dey and Mishra 2017):

$$ AE=P-H $$
(13)

where:

AE:

annual actual evapotranspiration (mm)

P:

annual precipitation (mm)

H:

annual runoff (mm)

In this study, the commonly applied Penman-Monteith equation is used to determine PET that determines the evapotranspiration from the hypothetical grass reference surface. In case of the Zagożdżonka catchment, monthly average data, measured at the nearest meteorological stations at three locations in Kozienice, Puławy and Lublin are used to estimate monthly potential evapotranspiration, according to the formula (Allen et al. 1998):

$$ {PET}_{day}=\frac{0.408\Delta \left({R}_n-G\right)+\gamma \frac{900}{T+273}{u}_2\left({e}_s-{e}_a\right)}{\Delta +\gamma \left(1+0.34{u}_2\right)}, $$
(14)

where:

PETday:

potential evapotranspiration (mm day−1),

Rn:

net radiation at the crop surface (MJ m−2 day−1),

G:

soil heat flux density (MJ m−2 day−1),

T:

air temperature at 2 m height (°C),

u2:

wind speed at 2 m height (m s−1),

es:

saturation vapour pressure (kPa),

ea:

actual vapour pressure (kPa),

Δ:

slope vapour pressure curve (kPa °C−1),

γ:

psychometric constant (kPa °C−1).

3.4 Land Use History

Land use changes in the study catchment are estimated based on the available cartographic material. For the initial period of research, topographic maps at a scale of 1:50000 and 1:25000, valid for the years 1974 and 1982 are available (GUGIK 1974, 1982). For the later periods, data collected under the Corine Land Cover programme (CLMS 2020) during the years 1990, 2000, 2006 and 2018 are analysed to determine the land use structure and possible changes, as well as the time periods of these changes.

4 Results

4.1 Analysis of Long-Term Hydro-Meteorological Records

Figures S2 and S3 (see the Online Resources) present the variability in precipitation, runoff, air temperature and actual and potential evaporation over the period 1963–2018. An increasing trend in the mean annual air temperature and in the annual potential evapotranspiration is observed, whereas the measured runoff depth decreases over time. No trend could be observed for annual precipitation or for actual evaporation. These observations confirm the results of our previous study on environmental changes in this catchment (Krajewski et al. 2019). The visible variations of hot and cool, and dry and wet years can be assigned to the natural climate variability. Despite this, it seems that over the last few decades the climate has become warmer and drier as compared to the beginning of observation period. This observation correlates with the general trends estimated for Poland, based on the years 1951–2000 (Degirmendžić et al. 2004).

4.2 Identified Land Use Changes

The structure of the catchment is dominated by two land use forms: arable land and forests (Table 1). However, their fraction varies over the observation period. During the 1960s to 1980s, each of these land use forms covers around 42% of the study catchment. Since the 1990s, a gradual increase in forest areas has been observed and the percentage of agricultural areas has decreased. Therefore, arable lands have been partially left as fallow and thus the ecological succession has started. As a result, a rapid increase in the ratio of the forest areas can be observed during the period 2001–2006. Currently (2018), forests cover 56% of the catchment and arable lands, only 29%. In contrast to these changes identified, fractions of meadows, residential areas, wetlands and roads remain constant throughout the entire observation period. Small differences in these ratios, estimated for subsequent years, are attributed to inaccuracies of the maps. Based on the analysis of land use changes, two main sub-periods may be identified in the catchment history; the first period with a relatively stable land use structure spans the beginning of the observation period (1963) until around 1990, and the second period with a gradually increasing quantity of woodland starts at around 1990 and has lasted until recent years (2018).

Table 1 Land cover in the Zagożdżonka River catchment up to the Płachty station
Full size table

4.3 Identified Change Points

Changes identified from land use history were next used as information for localizing change points in recorded runoff data. Based on the annual runoff estimates, the change point was localized in 1982 (see Table 2). In relation to other climatic variables, change points were localized in different years. Generally, any changes were firstly noted in terms of precipitation, even in 1980, while changes were observed for the potential evapotranspiration in 2001. All these detected shifts in hydro-climatic variables which contribute to a reduction of the available water resources (with a lower precipitation and runoff, and a higher temperature and evaporation). As these changes occurred after one other, their influences on water resources cumulate. Based on these observations and having knowledge of the land use history, it can be assumed that change points split the observation period into two sub-periods: the pre-change period without any climate and land use changes (1963–1982) and the post-change period with land use and climate changes present (1983–2018).

Table 2 Identified change points for analysed hydro-meteorological variables
Full size table

4.4 Quantified Climate and Land Use Change Impacts on Streamflow

4.4.1 Results from the Conceptual Approach

Both sub-periods, i.e., pre-change and post-change, were further analysed to evaluate the human and climate impacts, as referenced in Eqs. (1) and (2).

Firstly, based on the Tomer and Schilling method, it was computed that over the analysed period, the energy exceed (Eex) increased from 0.260 to 0.314 and the water exceed (Pex) decreased from 0.218 to 0.149. Following the description in Table S1 (Online Resources), it can be stated that changes in runoff are primarily caused by shifts in climatic factors and to a lesser extent due to land use changes.

Secondly, Budyko curves, according to seven different formulas, (Table S3, Online Resources) have been established based on records from the years 1963–1990, for which no significant changes in the land use structure occurred (section 4.2). Despite this, a large spread of observation points can be noted with points oscillating around the established Budyko curves (Fig. 2). Such a high variability in observation points was also noted by other authors (Gentine et al. 2012) and has been explained by year-to-year deviations of annual precipitation and evaporation records from the long-term averages. It may also be observed that certain of the constructed Budyko curves have a very similar shape, and some even overlap with one other. Among the seven forms of the Budyko curves analysed, that proposed by Milly (1993) was characterized by the lowest error of estimate and thus was the best fit in terms of the observed data (see Table 3).

Fig. 2
figure 2

Established Budyko curves for the Zagożdżonka River catchment up to the Płachty gauging station. Points represent hydro-meteorological monitoring records over the period 1963–1990 (period with a stable land use structure)

Full size image
Table 3 Fit quality of the analysed Budyko curves (standard error) and results of the Budyko curve decomposition method (ΔQ till ΔQC)
Full size table

Next, the contributions of land use and climate change to the runoff change were quantified according to the aforementioned decomposition method. For two of the applied curve forms, i.e., Budyko (1974) and Zhang et al. (2001), it was not possible to quantify the contributions because of a high error of estimate, which limited their applicability. According to the other five curves, climatic factors were primarily responsible for runoff changes in this catchment (Table 3). In detail, a decomposition of the Milly (1993) curve indicated that the reduction of runoff (−51.9 mm on average) was caused primarily by climate (65%) and less by land use changes (35%). An analysis of the Fu (1981); Yang et al. (2008); Wang and Tang (2014) curves gave very similar results with climate change accounting for around 80% and land use changes for around 20%. Finally, the importance of land use change was estimated at only 12% when applying the Zhou et al. (2015) curve. These findings show that the dominance of impacts was determined in the same way, independently of the applied curve form, however, their exact contributions varied for different curves.

4.4.2 Results from the Analytical Approach

Two methods were used: the climate elasticity and the hydrological sensitivity. In the first method, the elasticity coefficients were determined based on the three selected forms of Budyko curves that were characterized by the lowest, median and highest error of estimate, i.e., according to Milly (1993); Fu (1981) and Zhang et al. (2001), Table 4. The results obtained for the first two curves (Milly and Fu) were similar to the contributions of human and climate impacts, estimated according to the decomposition method (compare with Table 3). In the case of the Zhang curve, a slight dominance of land use changes (56.8%) over climate change (43.2%) was estimated. Note however that this curve had the highest error of estimate and thus this finding should be treated with caution.

Table 4 Established parameters in climate elasticity and hydrological sensitivity methods
Full size table

Finally, the contributions of human and climate impacts on runoff conditions were quantified using the hydrological sensitivity method with two formulas for estimating the sensitivity coefficient (Table 4). Regardless of the formula applied, very similar outcomes were obtained, with a dominant contribution of climate change, responsible for around 80% and the land use change responsible for around 20% of the decrease in runoff in the studied catchment over the analysed period.

5 Discussion

Our results demonstrated that in the catchment of the Zagożdżonka River, both land use changes and climate changes occurred over the studied period 1963–2018. The area of arable lands decreased by almost 15%, while the fraction of forests increased by the same amount. Other land use changes were minor. Based only on analyses of land use maps that are available at irregular time periods, particularly in past years, i.e., before the year 1990, one cannot deduce when exactly the important changes in the catchment land use occurred. In this context, the change point tests enabled the precise identification as to when a shift in recorded data occurred. In our case, this change point was found to be in 1982 and it splits the observation period into pre- and post-change sub-periods of distinctive characteristics. In the post-change period (1983–2018) the average annual temperature increased by 1 °C (12% of the long-term average), while the total annual precipitation decreased by 67.9 mm (13% of the long-term average). These changes contributed to a decrease in the average annual runoff of 51.9 mm (49% of the long-term average).

An identification of change points does not provide any information relating to the reason for the change, observed in the annual runoff, i.e., whether this change occurred due to land use or climate change. For this purpose, other methods that enable the decomposition of these effects must be applied. In this work, four different methods were used to quantify these effects. Three of them (decomposition method, climate elasticity and hydrological sensitivity) use the functional form of the Budyko curve, whereas the fourth method (Tomer and Schilling) relies on the proportion in the precipitation, actual and potential evaporation. In contrast to the first three methods, the latter approach does not enable the quantification of contributions of changes and thus can only be applied to identify a dominant source of change. All other three approaches indicated that climate shifts played a dominant role in changing the water resources (annual runoff) in the study catchment. However, quantified contributions differed, depending on the approach used. Among seven analysed forms of the Budyko curve, that proposed by Milly (1993) had the lowest error of estimate in the study catchment. The results obtained, according to the decomposition and climate elasticity methods (with the use of Milly’s equation), seem to be consistent and indicate that climate change had a higher impact (60%) on streamflow reduction, rather than land use changes (40%). Note that an equation for sensitivity coefficients according to the Milly curve (1993) does not exist (see Table S3, Online Resources). By using the Fu (1981) equation (characterized by a higher error of estimate), similar results were obtained for all three methods, with climate and land use change contributions to the streamflow change equalling 80% and 20%, respectively. The largest differences between the three methods applied were observed when applying the Zhang et al. (2001) curve, which can be explained by the fact that this form fitted the recorded data least well.

These findings demonstrate, firstly, that the methods applied are applicable to small catchments (<100 km2) to decompose the effects of land use and climate change on water resources. As seen in the example of the Zagożdżonka River, with a transparent land use change history, both land use and climate change contributions could be quantified. Secondly, our findings manifest the importance of the Budyko curve form which is the key element of all three methods. Hence, its correct determination is of primary importance. Our results showed that the choice of the best form of the Budyko curve is more important than the choice of the method for decomposing changes.

Such information on the source and importance of change contributions (land use or climate change) is particularly important for better planning strategies for water management in the catchment. In the case of the Zagożdżonka River studied here for which land use changes were quantified as being responsible for 20 to 40% of the total decreases in runoff, small retention measures could be planned to retain water during high flows and release it during low flows.

For other similar small catchments, authors recommend choosing an appropriate form of the Budyko curve first and using one of the three methods (decomposition method, climate elasticity and hydrological sensitivity) to quantify land use and climate change impacts on water resources. The Tomer and Schilling method could only be recommended to determine the dominance of the impacts. The decomposition of the climate and land use changes should always be proceeded by the detection of change points and should be supported with analyses of the land use history.

6 Conclusions

In this study, four different available approaches were tested to separate land use and climate change impacts on water resources in a small catchment (<100 km2) using long-term observations between 1963 and 2018. Based on our results, the following conclusions can be drawn:

  1. I.

    In the study catchment of the Zagożdżonka River, land use changes (increase in forest areas) and climate changes (increase in annual evaporation, decrease in annual precipitation) occurred and affected the streamflow. In the post-change period (since 1983) the annual runoff decreased by 51.9 mm (49% of the long-term average),

  2. II.

    Quantified changes obtained, based on four methods, were consistent with the change in runoff, primarily caused by shifts in climatic variables. However, quantified changes varied depending on the applied method and the chosen form of the Budyko curve. Hence, special care should be taken to select a suitable form of the Budyko curve for the decomposition, climate elasticity or hydrological sensitivity methods. The fourth method (Tomer and Schilling 2009) does not provide quantitative contributions in relation to the impacts.

  3. III.

    In our case, the form of the Budko Curve, proposed by Milly (1993) fitted the measured data best. The estimated contributions of climate and land use changes to the decrease in mean annual runoff in the studied catchment, amount to between 60% and 80% and between 40% and 20%, respectively.

  4. IV.

    Our results demonstrated the suitability of the applied methods for quantifying the sources of runoff changes in similar small catchments, which should result in better planning of water resources management in these catchments.