1 Introduction

Global water resources are rarely distributed in proportion to the population density of any particular region (Oki and Kanae 2006). Mekonnen and Hoekstra (2016) estimated that 4 billion of the world’s population encounter water scarcity, for at least a short period of time in a year. Therefore, water scarcity is one of the major issues facing different societies today. In addition, climate change is a growing factor that is affecting water systems, hydrological cycle, and its regime (Hallett 2002). Alterations in the hydrological cycle have severe impacts on the environmental, economic, and social aspects of societies. Moreover, the variability in water resource availability, due to global warming and distribution of the population in different areas, will affect the estimations of the impacts of climate change (Arnell 2004).

The IPCC technical summary (Stocker 2014) pointed out that the Global Mean Surface Temperature (GMST) has increased excessively in the past three decades, with 2000–2010 being the warmest decade noted. Moreover, Xu et al. (2017) concluded that the increase in global mean land surface temperature during 1900 to 2014 was 0.083 ± 0.005oC per decade.

Furthermore, precipitation has increased in the northern hemisphere’s mid to high latitudes from 1901 to 2010 (Gu and Adler 2015); however, in subtropical and tropical areas, precipitation has reduced. Despite these results, the IPCC technical summary (Stocker 2014) stated that there is only “medium confidence” that the change in global precipitation pattern is due to human activities; but it is “likely” that the global trend towards having more heavy precipitation events has increased since 1950.

Changes in hydrological regimes will clearly result in changes in river run-off and discharge. Asadieh et al. (2016) showed that the global run-off during 1971–2001 has decreased by about 0.042% each year.

Accordingly, climate change alters the availability of water resources in different regions (Gohari et al. 2017), impacts on hydrological cycles (Nijssen et al. 2001) and causes increases in the number of extreme events such as drought and flood (Hirabayashi et al. 2013; Prein et al. 2016). Also, climate change increases the water scarcity (Schewe et al. 2014; Madani et al. 2016), as well as environmental stress (Harley et al. 2006; Walther 2010) and decreases food security (Stevens and Madani 2016). Therefore, adaptation to climate change is a crucial fact facing human societies. Adaptation to climate change is also essential due to the long-term response of the climate system to the changes (Grothmann and Patt 2005). This means that even with mitigation policies and limiting GHG emissions, the global temperature will continue to increase, thereby demanding adaptation. Accordingly, evaluating climate risks and their associated vulnerabilities contributes to the selection of optimal sustainable adaptation strategies (Noble et al. 2014).

Analysing the adaptation strategies needs a comprehensive insight into the system’s performance in the changing climate (Asefa et al. 2014). Ahmad and Haie (2018) developed a framework to analyse the impact of climate change and population growth on the performance of a basin in Nigeria by considering “sustainable efficiency” which takes into account the quantity and quality of water use. Sordo-Ward et al. (2019) also analysed current and future water availability under climate change effects. They further evaluated different adaptation policies, i.e., water allocation, reservoir capacity design, and modifying urban water usage patterns.

Reliability-Resiliency-Vulnerability (RRV) indices, first introduced by Hashimoto et al. (1982), are widely used to evaluate the performance of a system. Kjeldsen and Rosbjerg (2001) used RRV indices to assess the sustainability of a water resource system. More recently, RRV measures have been used to evaluate the performance of a water system under varying climate conditions by considering future projection of a river run-off (Asefa et al. 2014), rainfall variability and drought patterns (Hazbavi et al. 2018), spatial distribution of available water (Sediqi et al. 2019), and water allocation (Zou et al. 2020).

This study aims to provide a hybrid adaptive framework to evaluate the historical and future performance of a water reservoir system under the effect of climate change. Our framework uses the historical climatic data of a water reservoir to calibrate a hydrological model to the system. The framework will then consider the future projection of hydrological cycle, i.e., precipitation, evaporation, and run-off, to evaluate the performance of the reservoir system by reporting the RRV measures. The framework is novel in that it calibrates the hydrological model to a system based on its historical data, and therefore can be used to evaluate the performance of any reservoir system. We believe that this understanding may help the water managers and authorities to develop more effective management strategies to accommodate the changes in the climate.

The paper is structured as follows: section 2 provides the dataset and methodologies used along with the schematic framework of the study, section 3 represents the results obtained from each of the framework steps in a real case study from a river located in the south-west of Iran.

2 Datasets and Methodology

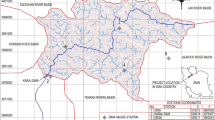
Dez dam is located in the south-west of Iran with a total capacity of 3315MCM and reservoir height of 203 m, see Fig. 1(a). The main purpose of the Dez dam is to supply water to irrigational districts and to support hydropower production.

Fig. 1
figure 1

(a) The Dez reservoir in Iran, (b) The proposed framework for analysing the effect of climate change on the Dez reservoir operation

Full size image

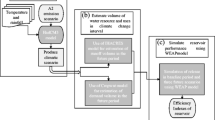
In the first step of our proposed framework, 26 years of monthly historical climatic data (e.g., precipitation, and evaporation) and the reservoir inflow from January 1980 to December 2005 are used to design the hydrological model of the reservoir system. The hydrological model is optimised to obtain the optimal release policies. The historical water release from the Dez reservoir is further used to validate the optimised policies and the framework that investigates the effect of climate change on the Dez reservoir performance. General Circulation Models (GCMs) are then used to analyse future projections. Each GCM is defined by four Representative Concentration Pathways (RCPs) to introduce low, intermediate, and high radiative forcing concentration. However, due to uncertainty of the GCMs, in many climate impact studies (Gosling et al. 2017; Fazeli Farsani et al. 2018) more than one climate model is used to evaluate future climate and hydrological variability. Therefore, in this study, the effect of climate change is investigated for the period of 2006 to 2100 using three GCMs, namely HadGEM-ES (Collins et al. 2011), MIROC5 (Watanabe et al. 2010), CCSM4 (Gent et al. 2011). Figure 1(b) represents the proposed framework to analyse the effect of climate change on the reservoir operation in the Dez reservoir. All model development was undertaken using the MATLAB numerical computing platform (MATLAB 2019). The framework that has been developed consists of 5 main stages that were directly implemented as a cascade of MATLAB functions.

2.1 Reservoir Model

A reservoir’s behaviour can be defined by its storage and inflow in the operation horizon. However, the trajectories of these values for the future are not known. Thus, in order to be able to make decisions for the future operation of a reservoir, a numerical model is calibrated to match the operational behaviour of the current system.

2.2 Mass Balance

The reservoir is modelled by its mass-balance equation (Soncini-Sessa et al. 2007), as follows:

$$ {s}_{t+1}={s}_t+{q}_{t+1}+{P}_{t+1}-{E}_{t+1}-{r}_{t+1} $$
(1)

where st is defined as the storage of the reservoir at time t, qt + 1 is the amount of inflow entering the reservoir from time t to t + 1. Et + 1 and Pt + 1 are defined as the evaporation and precipitationon on the reservoir surface in the time interval of [t, t + 1), respectively. To simplify the modelling, Dez reservoir is considered to be cylindrical, having a surface area of S. Therefore evaporation and precipitation on the reservoir can be defined as:

$$ {E}_{t+1}=S.{e}_{t+1} $$
(2)
$$ {P}_{t+1}=S.{p}_{t+1} $$
(3)

where et + 1 and pt + 1 are the specific evaporation and precipitation, respectively. Accordingly, net inflow into the reservoir, nt + 1, in [t, t + 1) is defined as:

$$ {n}_{t+1}={q}_{t+1}+{P}_{t+1}-{E}_{t+1} $$
(4)

In Equation 1, rt + 1 is the amount of water released from the reservoir in [t, t + 1), which is a function of storage, st, the net inflow, nt + 1, and the release decision, ut.

$$ {r}_{t+1}={R}_{t+1}\left({s}_t,{n}_{t+1},{u}_t\right) $$
(5)

Equation 5 is a non-linear stochastic relation between the actual release from the reservoir, rt + 1, and the release decision, ut, that is made at time t (Piccardi and Soncini-Sessa 1991). This function can be defined as:

$$ {R}_{t+1}\left({s}_t,{n}_{t+1},{u}_{\mathrm{t}}\right)=\left\{\begin{array}{rr}{v}_t\left({s}_t,{n}_{t+1}\right)&\ \mathrm{if}\ {u}_t<{v}_t\left({s}_t,{q}_{t+1}\right)\\ {}{V}_t\left({s}_t,{n}_{t+1}\right)&\ \mathrm{if}\ {u}_t>{V}_t\left({s}_t,{q}_{t+1}\right)\\ {}{u}_t& \mathrm{if}\ {v}_t<{u}_t<{V}_t\end{array}\right. $$
(6)

where vt represents the minimum release from the reservoir by keeping all the gates closed and, likewise, Vt is the maximum release from the reservoir by keeping all the gates open (Castelletti et al. 2008).

2.3 Optimal Reservoir Policies

The operation policy of a reservoir determines the amount of water that should be released from the reservoir at each time step, defined as a function of the state variable, namely reservoir’s storage, st. The optimal operational policies can be obtained by mathematical optimisation techniques to evaluate the best values for the key objective functions. Stochastic Dynamic Programming (SDP) (Bellman 1957) is one of the most commonly used methods in finding the optimal operational policies of a reservoir system. SDP designs the operation policy of the system by making sequential decisions. At each time step, the decision, ut, generates an immediate cost, and changes the next state, st + 1, of the system (Soncini-Sessa et al. 2007). SDP is used to minimise the summation of all the immediate costs of two objectives; namely:

  1. 1

    Water Supply: Minimisation of monthly squared water deficit (for irrigation, domestic and industrial sectors), defined as the squared difference of water demand and water supply

$$ {J}^{deficit}=\Sigma \left(\mathit{\max}\left({\left({w}_t-{r}_{t+1}\right)}^2,0\right)\right) $$
(7)

where wt is the water demand.

  1. 2.

    Flooding around the catchment: Minimisation of flooding around the catchment of the reservoir, defined as the difference between the level of water in the reservoir and the height of the dam’s wall.

$$ {J}^{Flood}=\Sigma \left(\mathit{\max}\left(\left(H-{h}_{t+1}\right),0\right)\right) $$
(8)

where ht + 1 is the level of water in the reservoir in [t, t + 1) and H is the height of the dam’s wall from the foundation.

In this study, the SDP algorithm presented in the M3O MATLAB toolboxFootnote 1 (Giuliani et al. 2016) has been used to find the optimal policies. M3O is a flexible toolbox to design the Pareto Optimal operating policies of a water reservoir system.

To ensure that the design and optimal policies of Dez are modelled properly, the real release data of the reservoir during the same time period is used to validate the model.

2.4 Bias Correction of GCM Precipitation and Evaporation

Bias is defined as the difference between a mean of forecasted or modelled data and a mean of observed data over a definite time horizon (WMO 2009). There are many obvious reasons that cause bias in climatic model output, such as inaccurate atmospheric models, poor/incorrect initialisation, climate variability, and unrepresentative original datasets used for model calibration and validation (Maraun et al. 2010; Maraun 2012; Ehret et al. 2012). Therefore, it is essential to bias-correct the GCM precipitation and evaporation data to be used in the hydrological model of a system.

Quantile Mapping (QM) is a statistical method that intends to correct both mean and standard deviation of the model output (Panofsky and Brier 1958). QM uses the statistical distribution of a dataset and corrects its bias using Eq. 9.

$$ {x}_{m,p}^{\prime }(t)={F}_{o,h}^{-1}\left({F}_{m,h}\left[{x}_{m,p}(t)\right]\right) $$
(9)

where subscripts m and o denote the model and observed historical data, h and p denote the historical and projected period, respectively, and F represents the Cumulative Distribution Function (CDF) of the dataset. In this study, Kernel Density Distribution Mapping (KDDM) is used to minimise the bias of the GCM data. KDDM is a new form of QM to bias-correct climatic data (McGinnis et al. 2015), which has shown the best performance in the application of quantile mapping (McGinnis et al. 2015; French et al. 2017). KDDM considers non-parametric kernel distribution for both precipitation and evaporation.

2.5 Rainfall-Runoff Analysis

Reservoir inflow is a complex non-stationary timeseries with variable statistics over time that makes its modelling and predicting the future projections challenging (Supratid et al. 2017). The Discrete Wavelet Transform (DWT) has proven to be a powerful tool to overcome this non-stationary specification of reservoir inflow (Kumar et al. 2015; Shafaei and Kisi 2016; Shenify et al. 2016). Moreover, the Stationary Wavelet Transform (SWT) (Fowler 2005) is a form of DWT with a shift-invariant transform that can extract important temporal features of inflow time series in different levels of frequency resolution. SWT applies low and high-pass filters to inflow timeseries. Therefore, SWT decomposition decomposes the inflow, into low-frequency components or approximations, and high-frequency components or details. The approximation and detail sub-timeseries are linear combinations of low-pass and high-pass filtering basis functions in the wavelet environment.

In this study, the inflow into the reservoir with monthly timestep is first decomposed into approximation and detail coefficients using SWT. Then a Nonlinear Autoregressive Neural Network with Exogenous Factor (NARX) is used to predict each of the inflow sub-timeseries of the SWT. NARX predicts the inflow at time t + 1 using regression on previous values of the inflow and precipitation. Therefore NARX can be represented as:

$$ q\left(t+1\right)=f\left[q(t),q\left(t-1\right),\dots, q\left(t-{d}_q\right);p(t),p\left(t-1\right),\dots, p\left(t-{d}_p\right)\right] $$
(10)

where q(t) and p(t) are the inflow and precipitation at time t, respectively. dq and dp represent the time lag of exogenous input, p, and output regressor, q. f(.) shows the non-linear mapping that is obtained by applying a standard multilayer perceptron (MLP) (Supratid et al. 2017).

Accordingly, in this study, the original monthly inflow timeseries (1980–2005) is decomposed by three levels of SWT into approximation a3, details d1, d2, and d3 sub-timeseries. Then, 20 years of each sub-timeseries (1980–1999) along with corresponding exogenous input, precipitation, with time lag of three time steps (three months) is trained by NARX. At the end of the training phase, all the sub-timeseries coefficients are fed to an inverse SWT to reconstruct the inflow. The model is tested on six years of data (2000–2005) to validate the SWT-NARX model, see Fig. 2. Finally, due to the lack of data, the model is trained again on all the historical dataset (1980–2005) using 10-fold cross-validation and the original historical data is used as the starting seed into NARX to predict inflow projection. The predicted value is fed back to the algorithm as the output regressor along with the exogenous input, precipitation, which is obtained from the bias-corrected GCMs.

Fig. 2
figure 2

SWT-NARX framework for forecasting reservoir inflow (Supratid et al. 2017)

Full size image

2.6 RRV

Hashimoto et al. (1982) developed the Reliability-Resilience-Vulnerability framework (RRV) to show the performance of a reservoir.

  • Reliability defines the probability of a system to be in its satisfactory state during the time period under consideration. Hashimoto et al. (1982) describes Reliability as a random output variable of a system, Xt, at time t, which can be divided into two sets of states:

    • S: the set of ‘satisfactory’ state;

    • F: the set of ‘unsatisfactory or failure’ state.

Therefore, the ‘Reliability’ of a system is defined as the probability of the system having satisfactory output:

$$ Reliability= Prob\left[{X}_t\in S\right] $$
(11)

  • Resiliency describes the performance of the system by estimating how fast a system can return to a satisfactory state once it enters the failure state. Resiliency is an important index because if it takes too long for a failed system to go back to its normal condition, it may subsequently cause severe complications, such as permanent flooding and environmental damage (Hashimoto et al. 1982)

Resiliency can be defined as the “probability of going from failure state to a satisfactory state in one time-step”:

$$ Resiliency=P\left\{{X}_{t+1}\in S|{X}_t\in F\right\}=\frac{P\left\{{X}_t\in F\kern1em and\kern1em {X}_{t+1}\in S\right\}}{P\left\{{X}_t\in F\right\}} $$
(12)

Jain and Bhunya (2008) suggested that resilience with the definition described by Equation 12 can also be computed by:

$$ Resiliency=\frac{\# FtoS/\left(\# FtoS+\# StoF\right)}{\#F/\left(\mathrm{Total}\kern1em \mathrm{Period}\right)} $$
(13)

  • Hashimoto et al. (1982) defined Vulnerability as “the magnitude of the failure” and is defined as a weighted sum of severe outcomes of failure events, Equation 14

$$ Vulnerability={\Sigma}_{j\in F}{s}_j{e}_j $$
(14)

where sj represents severe outcome of a failure event, and ej is the probability of the system with unsatisfactory outcome.

3 Results and Discussion

All the numerical analysis in this study has been based on using monthly time steps. However, in order to represent a better understanding of the framework and the effect of climate change on Dez reservoir operation, the results are reported on a mean annual basis for 2020 (as average of 2010–2035), 2050 (average of 2036–2065), 2080 (average of 2066–2090), and 2100 (average of 2090–2100).

3.1 Hydrological Model of the Reservoir

In step 1 of the proposed framework, Fig. 1(b), the hydrological model of the Dez reservoir is designed and optimised to respond to the two objectives considered. The results obtained from the SDP optimal policies compared to the real releases, Fig. 3, shows an 81% correlation indicating that the SDP policies can be used to define the releases in future projections.

Fig. 3
figure 3

Actual average annual water release and modelled average annual water release from the Dez reservoir

Full size image

3.2 Bias Correction and Rainfall-Runoff Analysis

In step 2 of the framework, the GCM data are bias-corrected using KDDM. Table 1 shows that the mean modelled evaporation obtained from GCMs are much less than the real values of evaporation from the Dez reservoir. These values have been corrected using KDDM to minimise the difference between the bias-corrected modelled and real values. Accordingly, the same KDDM parameters obtained from bias-correction of historical data are used to reduce the bias for the projection of precipitation and evaporation. As shown in Fig. 4, all GCMs predict an increase in precipitation until 2100 compared to their historical values. However, the evaporation rates behave differently according to different climate models and across different RCPs.

Table 1 Mean values of observed, raw modelled and bias-corrected precipitation and evaporation data on Dez reservoir
Full size table
Fig. 4
figure 4

(a) Average precipitation, (b) average evaporation, and (c) average inflow projection of the Dez reservoir according to the three GCMs

Full size image

In step 3 of the framework, SWT-NARX is trained using 20 years of historical data (1980–1999) with 10-fold cross-validation and tested on the rest of the available historical dataset (2000–2005). The results show good performance in modelling the reservoir inflow from precipitation and previous inflow data with three-time step delays as seen in Table 2. However, due to small dataset, another SWT-NARX with 10-fold cross-validation is trained on the whole historical dataset to be used in predicting the run-off projection until 2100 to increase the quality of the prediction model.

Table 2 SWT-NARX model performance for Dez reservoir’s inflow
Full size table

The predicted run-off projection shows that all the climate models predict an increase in the inflow into the Dez reservoir until 2020, compared to average historical inflow, as seen in Fig. 4(c). This is followed by a decrease in the inflow until 2100.

3.3 RRV

In step 5, the RRV indices for water demand in the downstream of the Dez reservoir is calculated across three GCMs. According to Fig. 5, reliability and resiliency of Dez reservoir increases by 2100, compared to the historical performance. This shows that not only will the Dez reservoir be more capable of responding to water needs of downstream areas, but also the probability of the reservoir returning to satisfactory state after a failure event gets higher than its historical performance. However, Fig. 5(c) shows an increase in the vulnerability of the Dez system across most RCPs, indicating that despite the higher reliability and resiliency of the reservoir, the damages of a failure event will be more severe than historical performance. Zolghadr-Asli et al. (2019) also indicated that climate change will increase the reliability and resiliency of hydro-power production of the Karkheh reservoir, located in the same region in Iran, while the vulnerability will also increase and produce severe blackouts.

Fig. 5
figure 5

(a) Reliability (b) Resiliency (c) Vulnerability indices for the Dez reservoir

Full size image

Our results also show that considering the historical release policies of the reservoir and ignoring the effects of climate change in defining the operating policies will result in system failure and will produce serious damages. Therefore, in order to have a more effective water management policy, it is important to re-optimise the system’s operational policies considering the effect of climate change on the climatic data (Akbari-Alashti et al. 2018).

Moreover, the results show uncertainties in predicting the hydrological patterns due to uncertainties associated with GCMs. Therefore, it is essential to minimise these uncertainties by considering more than three climate models. Yet, adaptation policies should also consider these uncertainties for the probable future performance of the reservoir.

4 Conclusion

Climate change is expected to alter the hydrological regimes; therefore, predicting or forecasting the probable changes and their effect on water bodies are challenging. This study proposed a numerical framework for analysing the performance of reservoir operation under the effect of climate change. When applied to the Dez reservoir, as a case study, the results showed that by 2100 the reliability and the resiliency of the Dez reservoir increases in comparison to its historical performance. However, the vulnerability of the system also increases, which means that the consequences of failure states of the system will be more severe. Thus, the authorities should consider better adaptation policies for the Dez reservoir in order to minimise the damages caused by failure events.

This work demonstrates that analysing RRV indices and their projections from climate change under various scenarios can benefit regional authorities by giving them an idea of the difficulties that different regions may face. The information will enable water authorities to plan timely considerations for adaptation to the changes by re-optimising the reservoir release policies, changing water allocations, using other water supply sources, if available, and planning for enhancing possible infrastructures to reduce evaporation rates to avoid future undesired conditions. Moreover, the proposed framework can be applied to different stations at catchment level in order to develop tempo-spatial geo-maps. These maps can give more information of the future uncertainties of the whole catchment area and can result in better decision and policy making on a broader scale.

This study is the initial step in analysing reservoir performance under the effect of climate change by means of RRV indices, and it has been applied to only one reservoir in Iran. Future work on this study will include the application of the framework on more locations to discuss the effect of climate change on the RRV indices of reservoirs in other parts of the world.

4.1 Study Limitations

For practical purposes relating to the complexity of the model sedimentation was not considered in the modelling of the reservoir system. However, it is appreciated that considering the time-horizon of the study, sedimentation will affect the storage capacity and therefore the performance of the reservoir. Moreover, minimisation of sedimentation, maximising of the hydro-power production and any other objective concerning the reservoir system under study should further be considered.

Using only three GCMs is another limitation of this study. In order to lower the uncertainty involving climate models, it is essential to consider a larger ensemble of GCMs.