Skip to main content
SpringerLink
Log in

Modeling of Daily Rainfall Extremes, Using a Semi-Parametric Pareto Tail Approach

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

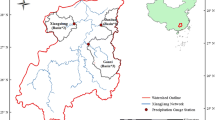
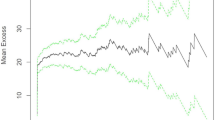
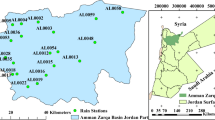
Various approaches have been widely proposed for simulation of the occurrence and the amount of daily rainfall. In this study, a piecewise distribution approach has been developed to improve extreme event amount simulation. The gamma-generalized Pareto (GGP) approach employs a combination of the generalized Pareto (GP) and the gamma density estimation method to model the daily rainfall distribution. Furthermore, three stochastic rainfall time series generations have been developed and compared to simulate the daily rainfall occurrence based on the first-order Markov chain (MC1), the second-order Markov chain (MC2) and the third-order Markov chain (MC3) approaches. 30 years daily datasets from 5 synoptic stations have been used in the semi-arid extra cold in Iran. The performance of different approaches has been compared using Akaike information climate criterion (AIC) and root mean square error (RMSE). Results show that MC1 performs relatively better than MC2 and MC3 for daily rainfall occurrence modeling. Results also show that the GGP probability density performs better to reproduce extreme daily rainfall compared with gamma, GP and exponential distributions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Akaike H (1974) A new look at the statistical model identification. IEEE T Automat Contr 19:716–723

    Article  Google Scholar 

  • Ben-Gai T, Bitan A, Manes A, Alpert P, Rubin S (1998) Spatial and temporal changes in rainfall frequency distribution patterns in Israel. Theor Appl Climatol 61:177–190

    Article  Google Scholar 

  • Byung-Jin S, Hyun-Han K, Dongkyun K, Seung OL (2015) Modeling of daily rainfall sequence and extremes based on a semi-parametric Pareto tail approach at multiple locations. J Hydrol 529:1442–1450

    Article  Google Scholar 

  • Daniel S (1985) Statistical methods in the atmospheric sciences. Dep of soil, Crop and Atmospheric Sciences, ITHACA, Cornell Univ, New York

    Google Scholar 

  • Dastidar AG, Gosh D, Dasgupta S, De UK (2010) Higher order Markov chain models for monsoon rainfall over West Bengal, India. IJRSP 39:39–44

    Google Scholar 

  • Furrer EM, Katz RW (2008) Improving the simulation of extreme precipitation events by stochastic weather generators. Water Resour Res 44:1–13

    Article  Google Scholar 

  • Hanum H, Wigena AH, Djuraidah A, Mangku IW (2015) Modeling extreme rainfall with gamma-Pareto distribution. Appl Math Sci 121:6029–6039

    Google Scholar 

  • Hyndman RJ, Koehler AB (2006) Another look at measures of forecast accuracy. Int J Forecasting 22:679–688

    Article  Google Scholar 

  • Katz RW (1981) On some criteria for estimating the order of a Markov chain. Technometrics 23:243–249

    Article  Google Scholar 

  • Khalili A (1997) Integrated water plan of Iran. Meteorol Stud, Ministry of power, Iran

    Google Scholar 

  • Li Z, Li Z, Zhao W, Wang Y (2015) Probability modeling of precipitation extremes over two river basins in northwest of China. Adv Meteorol 2015:1–13

    Google Scholar 

  • Liu C, Ikeda K, Thompson G, Rasmussen R, Dudhia J (2011) High-resolution simulations of wintertime precipitation in the Colorado headwaters region: sensitivity to physics parameterizations. Monthly Weather Rev 139:3533–3553

    Article  Google Scholar 

  • Mandal KG, Padhi J, Kumar A, Ghosh S, Panda DK, Mohanty RK, Raychaudhuri M (2015) Analyses of rainfall using probability distribution and Markov chain models for crop planning in Daspalla region in Odisha, India. Theor Appl Climatol 121:517–528

    Article  Google Scholar 

  • Mhanna M, Bauwens W (2011) A stochastic space-time model for the generation of daily rainfall in the Gaza strip. Int J Climatol:1–15

  • Mhanna M, Bauwens W (2012) Stochastic single-site generation of daily and monthly rainfall in the Middle East. Meteorol Appl 19:111–117

    Article  Google Scholar 

  • Moon SE, Ryoo SB, Kwon JG (1994) A Markov chain model for daily precipitation occurrence in South Korea. Int J Climatol 14:1009–1016

    Article  Google Scholar 

  • Moradi HR, Rajabi M, Faragzade M (2011) Investigation of meteorological drought characteristics in Fars province, Iran. CATENA 84:35–46

    Article  Google Scholar 

  • Mouelhi S, Nemri S, Jebari S, Slimani M (2016) Using the Markov chain for the generation of monthly rainfall series in a semi-arid zone. Open J Mod Hydrol 6:51–65

    Article  Google Scholar 

  • Nalbantis I, Tsakiris G (2009) Assessment of hydrological drought revisited. Water Resour Manag 23:881–897

    Article  Google Scholar 

  • Ng JL, Aziz SA, Huang YF, Wayayok A, Rowshon MK (2017) Generation of a stochastic precipitation model for the tropical climate. Theor Appl Climatol 133:489–509

    Article  Google Scholar 

  • Papalaskaris T, Panagiotidis T, Papadopoulos S, Pantrakis A (2016) Stochastic generation of daily rainfall, in Kavala city station, North- Eastern Greece. Procedia Eng 162:162–171

    Article  Google Scholar 

  • Paulo AA, Pereira LS (2007) Prediction of SPI drought class transitions using Markov chains. Water Resour Manag 21:1813–1827

    Article  Google Scholar 

  • Qian B, Gameda S, Hayhoe H (2008) Performance of stochastic weather generators LARS-WG and AAFC-WG for reproducing daily extremes of diverse Canadian climates. Clim Res 37:17–33

    Article  Google Scholar 

  • Sanusi W, Jemain AA, Zin WZW, Zahari M (2015) The drought characteristics using the first-order homogeneous Markov chain of monthly rainfall data in peninsular Malaysia. Water Resour Manag 29:1523–1539

    Article  Google Scholar 

  • Schoof JT, Pryor SC (2008) On the proper order of Markov chain model for daily precipitation occurrence in the contiguous United States. J Appl Meteorol Clim 47:2477–2486

    Article  Google Scholar 

  • Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6:461–464

    Article  Google Scholar 

  • Semenov MA (2008) Simulation of extreme weather events by a stochastic weather generator. Clim Res 35:203–212

    Article  Google Scholar 

  • Senthilvelan A, Ganesh A, Banukumar K (2012) Markov chain model for probability of weekly rainfall in Orathanadu taluk, Thanjavur District, Tamil Nadu. Int J Geom Geosci 3:191–203

    Google Scholar 

  • Shin JY, Lee T, Ouarda TBMJ (2015) Heterogeneous nixture distributions for modeling multisource extreme rainfalls. J Hydrometeorol 16:2639–2657

    Article  Google Scholar 

  • Soleh AM, Wigena AH, Djuraidah A, Saefuddin A )2017( Gamma distribution linear modeling with statistical downscaling to predict extreme monthly rainfall in Indramayu. 12th International Conference on Mathematics, Statistics, and Their Applications (ICMSA), Banda Aceh, Indonesia

  • Sonnadara DUJ, Jayewardene DR (2015) A Markov chain probability model to describe wet and dry patterns of weather at Colombo. Theor Appl Climatol 119:333–340

    Article  Google Scholar 

  • Srikanthan R, Pegram GGS (2009) A nested multisite daily rainfall stochastic generation model. J Hydrol 371:142–153

    Article  Google Scholar 

  • Srinivasareddy GV, Bhaskar RS, Purohit RC, Chittora AK (2008) Markov chain model probability of dry, wet weeks and statistical analysis of weekly rainfall for agricultural planning at Bangalore. Karnataka J Agric Sci 21:12–16

    Google Scholar 

  • Syafrina AH, Norzaida A, Noor Shazwani O (2018) Stochastic modeling of rainfall series in Kelantan using an advanced -weather generator. ETASR 8:2537–2541

    Google Scholar 

  • Tabari H, Zamani R, Rahmati H, Willems P (2015) Markov chains of different orders for streamflow drought analysis. Water Resour Manag 29:3441–3457

    Article  Google Scholar 

  • Tong H (1975) Determination of the order of a Markov chain by Akaike’s information criterion. J Appl Probab 12:488–497

    Article  Google Scholar 

  • van Montfort MAJ, Witter JV (1986) The generalized Pareto distribution applied to rainfall depths. Hydrolog Sci J 31:151–162

    Article  Google Scholar 

  • Vrac M, Naveau P (2007) Stochastic downscaling of precipitation: from dry events to heavy rainfalls. Water Resour Res 43:1–13

    Article  Google Scholar 

  • Wilks DS (1998) Multisite generalization of a daily stochastic precipitation generation model. J Hydrol 210:178–191

    Article  Google Scholar 

  • Wilks DS (1999) Interannual variability and extreme-value characteristics of several stochastic daily precipitation models. Agric For Meteorol 93:153–169

    Article  Google Scholar 

  • Woolhiser DA, Roldan J (1982) Stochastic daily precipitation models: 2. A comparison of distributions of amounts. Water Resour Res 18:1461–1468

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Water Science Engineering, Faculty of Agriculture, Bu-Ali Sina University, Hamedan, Iran

    Nadia Shahraki & Safar Marofi

  2. Department of Water Engineering, Kerman Graduate University of Advanced Technology, Kerman, Iran

    Sadegh Ghazanfari

Authors
  1. Nadia Shahraki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Safar Marofi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sadegh Ghazanfari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Safar Marofi.

Ethics declarations

Conflict of Interest

The authors express that there is no conflict of interests regarding the publication of this paper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shahraki, N., Marofi, S. & Ghazanfari, S. Modeling of Daily Rainfall Extremes, Using a Semi-Parametric Pareto Tail Approach. Water Resour Manage 33, 493–508 (2019). https://doi.org/10.1007/s11269-018-2112-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-018-2112-4

Keywords

Search

Navigation