1 Introduction

Short-term operation of reservoirs normally considers multiple purposes and face various uncertainties e.g., forecasted inflow. The optimization of reservoir operation is inherently a complex multi-objective problem under uncertainty, in which high-dimension decision variables and highly nonlinear constraints are often involved. The objective and/or constraint functions may be nonconvex, discontinuous (Labadie 2004; Geressu and Harou 2015) or noisy as uncertainty is incorporated (Gelati et al. 2014). In this context, the derivative information on either objectives or constraints often become unavailable, unreliable or impractical (Chen and Chen 2001; Guan et al. 2013), which may present a difficulty to the optimization methods in particular for derivative-based algorithms e.g., steepest descent or Newton method.

Over the last several decades, a number of optimization methods e.g., linear programming, dynamical programming and heuristic search algorithm have been developed and applied to reservoir operation (Yeh 1985; Labadie 2004). The optimization methods can be mainly classified into two types: global and local methods in terms of the ability for finding global optima or local one, or derivative-based and derivative-free methods in terms of the requirements of derivatives in the optimization procedure. Genetic Algorithms (GA) and its variants e.g., NSGA-II are global and derivative-free methods and have been widely applied to multi-reservoir operation during the last two decades (Oliveira and Loucks 1997; Malekmohammadi et al. 2009; Chen et al. 2015) owing to its robustness, effectiveness and global optimality properties. Other global and derivative-free methods such as particle swarm optimization (PSO) and Ant Colony Optimization (ACO) have also been used for optimization of reservoir operation (Baltar and Fontane 2008; Kumar and Reddy 2006). The aforementioned methods can be seen as strong candidates for optimizing short-term operation of multi-objective reservoirs under inflow uncertainty. However, like other random search methods, GA works by iteratively moving to better positions in the search-space, which are guided by the random process of the GA operators i.e., selection and crossover. The embedded randomness of GA is a key element for global optimality, however, this method has a slow convergence compared to methods that use derivative information, especially when approaching to the optimal point (Erol and Eksin 2006; Ishibuchi et al. 2009).

To improve the efficiency of the GA, Genetic Local Search Algorithm (GLSA) which combine local search methods with the GA, have been extensively reported in the literature (Knowles and Corne 2000; Harada et al. 2006; Derbel et al. 2012). The general idea of the GLSA is to incorporate a so-called local search method (LSM) as an extra optimizer in the process of the GA optimization. Coupling a LSM and GA is normally done using a serial or concurrent procedure. Serial approach applies the LSM by predefining a switching time (Leiva et al. 2000; Emmerich et al. 2007). Although this approach guarantees a local optimum with improved speed of convergence, the optimal switch timing is not known a priori on most practical problems. A recent study proposed a concurrent approach embedding a sequential quadratic programming (SQP) within NSGA-II (Sindhya et al. 2011). In the concurrent approach, some or all of the intermediate solutions from the GA were regularly modified by the LSM during the process. The SQP is treated as another operator in the GA to avoid the switch timing.

Regardless of serial or concurrent procedures, incorporating the LSM into GAs faces two major challenges when applying to multi-objective reservoir operation under uncertainty. The first one is the exchange of objectives between the LSM and GA. On one hand, a multi-objective GA (e.g., NSGA-II) can directly handle multiple objectives of the reservoir operation by using the non-dominated concept to find the Pareto optimal solutions (Deb 2012). On the other hand, the LSM often scalarize multiple objectives into a single objective e.g., a weighted sum (Ishibuchi et al. 2003). It has been shown that most popular linear scalarizations fail to find global optima for non-convex problems (Miettinen et al. 2008). Therefore, the linking of single objective in the LSM with multiple objectives in the NSGA-II is key for the success of hybrid optimization. The second challenge is that most of the LSM require first order or even second order derivatives to decide the search direction (Battiti 1992). This requirement largely limits the application of GLSA for multi-objective reservoir operation under uncertainty as the derivative information may not always be available in the presence of discontinuous or noisy objective/constraints functions.

The present study proposes a hybrid optimization model which aims to overcome the two aforementioned challenges. To achieve this goal, a concurrent hybridization scheme is used together with the Mesh Adaptive Direct Search (MADS), which is a pattern-based search method, as an additional step in the NSGA-II. Instead of using the weighted sum approach, an achievement scalarizing function (ASF) is introduced in the MADS to handle the objective exchange and ensure a Pareto optimal solution. A parallel optimization scheme is adopted for the MADS to simultaneously refine the multiple intermediate solutions from the NSGA-II process, allowing an efficient exchange of the solution vector. The MADS as well as the NSGA-II do not rely on derivative information and consequently, the hybrid model is entirely derivative-free. The superiority of the hybrid optimization model is demonstrated using a case study of a multi-objective reservoir system on the Columbia River. The frequency of applying the MADS in the routine of NSGA-II is investigated. The major contributions of the study are (1) development of a hybrid optimization model that couples the MADS and the NSGA-II for multi-objective short-term reservoir operation under uncertainty; (2) providing recommendation of a hybrid scheme that balances optimization performance and computational cost. The novelty of the paper is the development of a derivative-free model that has a relatively fast convergence, which could have broad applications in optimization of complex water resources systems.

2 Methodology

2.1 NSGA-II

NSGA-II is a widely used random search method for multi-objective problem (MOP) and have increasingly received attention for reservoir operation (Atiquzzaman et al. 2006; Chen et al. 2016). The NSGA-II is a member of the GA family and follows the primary principles of the classical GA. First, a set of candidate solutions (population) are randomly generated (first generation) that is essentially white noise. By using the selection operator, some candidate solutions from the population are selected. A so-called binary tournament is implemented and the chosen candidate solutions are compared in pairs based on the evaluation of constraints and objectives. The winners of the tournament reproduce the next generation by using recombination and mutation operators. The next generation can be viewed as random generation around the parent by some forms of distributions. The evolution process continues until meeting the stopping criteria. One of the most common stopping criteria is the number of generations. This criterion is problem-dependent, but generally a large number of generations can be used for ensuring solution convergence. The global optimality of the NSGA-II has been proved in many applications which are non-convex and even discontinuous problems (Deb et al. 2007; Deb & Jain, 2012).

2.2 MADS

The MADS belongs to the family of pattern search (PS) methods. Similar to other members of the PS family e.g. Generalized Pattern Search (GPS), the MADS does not require gradients for the optimization. The MADS is an iterative algorithm which aims to minimize a function f over a set Ω by evaluating f at some trial points. Each iteration of the MADS contains two steps, namely the search step and the poll step. The search step generates a finite number of mesh points and compare their objective function with the best feasible objective function value found so far (called current incumbent solution). The poll step is implemented whenever the search step fails to generate an improved mesh point. The poll step uses a parameter called poll size to dictate the magnitude of distance from the trial points generated in this step to the current incumbent solution. Compared to the GPS, the MADS is not restricted to a finite number of search directions, and results in a much better local exploration of the space of variables, in particular for the problem with nonlinear constraints (Audet and Dennis Jr 2006). Recently, the MADS has been increasingly used for complex engineering optimization problems, such as chemical processes and fluid structures (Audet et al. 2008; Long et al. 2014). It should be noted that, other derivative-free local search methods such as Hooke-Jeeves direct search can be selected for hybrid optimization as well. The comparison between different local search methods for hybrid optimization is not within the scope of this study but can be explored in the future.

2.3 Hybrid Optimization Model

Combining the NSGA-II and the MADS is expected to improve the optimization performance by enhancing local refinement during the global search. Alternating the use of the NSGA-II and the MADS is similar to the concept of exploration and exploitation. The former helps to locate the global optimal by exploring the entire search space and the latter contributes to a faster convergence by exploiting the search within a small region. A step-by-step procedure for setting up the hybrid optimization model is presented below:

  1. (1)

    Determine parameters for NSGA-II e.g., population and generation;

  2. (2)

    Determine parameters for MADS e.g., poll size and stopping criteria;

  3. (3)

    Set up interface between NSGA-II and MADS, e.g., exchange of objectives;

  4. (4)

    Start NSGA-II and run for a pre-determined number of generations;

  5. (5)

    Pause NSGA-II and pass the intermediate results to MADS; Start the MADS;

  6. (6)

    Run MADS until the stopping criteria is meet and pass updated results back to NSGA-II;

  7. (7)

    Repeat steps (4) to (6) until the predefined frequency of running MADS is meet;

  8. (8)

    Run NSGA-II until the predefined generation number is meet.

The implementation of the hybrid optimization model requires a number of considerations which are briefly discussed below:

2.3.1 Exchange of the Objective Between NSGA-II and MADS

The multi-objective from NSGA-II needs to be transformed to a single objective for MADS optimization. For facilitating the exchange of objectives, an achievement scalarizing function (ASF) is introduced. The ASF is a reference-point based method that has shown the ability to produce proper Pareto optimal solutions (Wierzbicki 1982). The reference point is usually specified by a decision maker (DM) and contains DM’s aspirations about desirable objective values. An example of constructing an ASF is shown below:

$$ \mathrm{ASF}\left(f(x),\upvarepsilon \right)={\max}_{i\in N}\Big({\varepsilon}_i\left({f}_i(x)-{f}_i^R\right)+\uprho {\sum}_{i=1}^N{\varepsilon}_i\left({f}_i(x)-{f}_i^R\right) $$
(1)

where f(x) is a summation of all the objective functions (multi-objective). The index i represents the ith objective and N is the total number of objectives. The parameter ρ is a sufficiently small positive scalar and ε is an N-vector of non-negative coefficients used for scaling purposes, i.e., normalizing objective functions of different magnitudes.

The first term of the ASF in Eq. (1) refers to weakly Pareto optimal solutions, i.e. a solution, which can be improved for at least one objective. The second one in Eq. (1) is an augmented term, which is used to guarantee that the obtained solutions have at least proper Pareto optimality, which generally is a subset of the Pareto optimal solutions. In this study, the parameter ρ in eq. (1) is set to a small value (0.001), as suggested in Miettinen and Mäkelä (2002) and Sindhya et al. (2011). The parameter ε is determined as \( {\varepsilon}_i=\frac{1}{z_i^{max}-{z}_i^{min}} \) for normalization purposes, where zmax and zmin are maximum and minimum objective values in the obtained solutions, respectively. It is usual and reasonable to start the NSGA-II first to avoid the local optima and then switch to the MADS. Therefore, the obtained solutions can be viewed as the current best solutions from the NSGA-II process. Each point in the objective space of the obtained solutions is then selected as a reference point and consequently, the \( {f}_i^R \) becomes known.

Every time when switching from the NSGA-II to the MADS, the ASF is formulated for each intermediate solution from the NSGA-II and the MADS is started for optimizing the resultant single objective. It is noted that the number of intermediate solutions from the NSGA-II can be as many as the population number e.g., 50. Therefore, for improving computational efficiency, a parallel computation approach was adopted by using the so-called “island model”. Each MADS process is individually run until the stopping criteria i.e., a small difference in the objective is satisfied. Each MADS solution is collected and the corresponding result of decision variables is stored in a pool. The pool is then used to replace the current chromosome of the NSGA-II, i.e., solutions in decision space that were obtained by the NSGA-II.

2.3.2 Starting Time of the MADS

The first aspect in hybridizing the NSGA-II and the MADS is the starting time of the MADS. Previous researches have shown that the NSGA-II is superior in finding feasible solutions in a complex search space (Ray et al. 2009; Wang et al. 2011). Therefore, the NSGA-II is first utilized to efficiently handle the constraints. It normally takes a certain number of generations e.g., 100 to obtain feasible solutions and this number is expected to be increased for optimization problems with a complex search space. During the process of finding feasible solutions, the candidate solutions in the NSGA-II tend to be clustered around the one which has the least constraint violations. The solutions then begin to spread after a feasible one is obtained. Since local search is applied to only good offspring from the NSGA-II (Ishibuchi et al. 2003), it is reasonable to start the MADS when the solutions of the NSGA-II have been spread out widely and evenly. In this case study, 1000 generations of the NSGA-II is found to be a good starting time for the MADS. However, this timing may be problem-dependent and it is left for future work.

2.3.3 Search Depth of the MADS

In the context of exploration and exploitation, search depth of the MADS represents the extent of exploitation. In our study, the stopping criteria of “objective difference” is implemented for determining the search depth of the MADS. The MADS search stops when the difference of the objectives between two consecutive iterations is smaller than 10−3. Other alternate options e.g., number of iterations can be used for determining the search depth; however, these are problem-dependent. The threshold on the objective difference is more general and flexible to different problem representations.

2.3.4 Search Frequency of the MADS

The key parameter for hybridizing a local and global method is the search frequency of the local method, which is defined as the number of implemented local searches during the process of global optimization. Too many local searches may significantly degrade the diversity of the solutions from global search and too few may result in a slow convergence (Ishibuchi et al. 2003; Sindhya et al. 2011). To investigate the effect of search frequency of the MADS on the overall performance of the optimization, various frequencies, ranging from 0 (i.e., NSGA-II only) to 10 are simulated. The performance of the optimization results are then compared for various search frequencies.

3 Case Study

3.1 Reservoir System

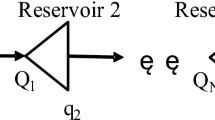
A reservoir system on the Columbia River in the United States, which comprises 10 reservoirs, is used as a test case. The sketch of the ten-reservoir system is shown in Fig. 1. The reservoir system provides multiple operational purposes including hydropower generation, ecological and environmental requirements and recreation (Schwanenberg et al. 2014).

Fig. 1
figure 1

Sketch of the ten-reservoir system in the Columbia River

Full size image

Because the short-term reservoir operation involves a time horizon of about two weeks, the operational horizon in our case study is set to two weeks. Due to data availability, the period from August 25th to September 7th is considered herein. The decision variables are the hourly outflows from each reservoir during the optimization horizon, which results in a total of 3360 decision variables.

3.2 Inflow Uncertainty

Two inflows are considered, one inflow to the GCL Reservoir and another to the LWG Reservoir (see Fig.1). Uncertainty in inflow can be caused by a number of reasons, including uncertainty in forecasting. Typically, the forecasting uncertainty is smaller at the beginning of the forecast period as information is more abundant and accurate, and tends to grow over time as information become less available and precise. The uncertainty associated with inflows can be illustrated by perturbing the historical record with a random linear function in time, as shown in Fig. 2. Six different time series data are used to represent 6 forecasting scenarios. It is noted that this inflow perturbation is solely for illustrating uncertainty. An ensemble of forecasts (Stedinger et al. 2014), each of which is an output from a simulation model (e.g., weather model), is a more accurate representation of uncertainty, and should be used for uncertainty quantification whenever they are available.

Fig. 2
figure 2

Illustration of inflow uncertainty

Full size image

3.3 Objectives

Two objectives related to hydropower generation are explicitly considered and expressed as follows:

$$ \mathit{\operatorname{Minimize}}\sum \limits_{t=1}^{T_k}\left(\min \left(0,\sum \limits_{i=1}^{N_r}\left({PG}_t^i\right)-{PD}_t\right)\right) $$
(2)
$$ \mathit{\operatorname{Maximize}}\sum \limits_{T_d-1}^{14}\Big(\sum \limits_{hr=6}^{22}\left(\max \left(0,\sum \limits_{i-1}^{N_r}{PG}_{hr}^i-{PD}_{hr}\right)\right) $$
(3)

where PG is hydropower generated in the system (MWh), PD is power demand in the region (MWh), t denotes time in hours, Th is the optimization period in hours (336 h), the index i represents reservoir identification number in the system and Nr is the total number of reservoirs. The variable hr represents heavy load hours (HLH), which in a typical day takes place from 06:00 am (06:00 h) to 10:00 pm (22:00). The variable Td corresponds to the optimization period in days (14 days in this case).

The first objective (Eq. 2) aims to minimize the power deficit during the operational horizon. The function min(0, *) expresses that the deficit is equal to 0 if the total power generated is greater than or equal to the power demand at time t. The second objective (Eq. 3) aims to maximize hydropower generation during heavy load hours for selling power to the electricity market at a higher price, which would increase the revenue. The function max(0, *) expresses that the objective value is equal to 0 if the total power generated is smaller than or equal to the power demand at heavy load hours. In the optimization model, the two objectives are transformed as minimization functions and normalized using a dimensionless index between zero and one. Other purposes of reservoir operation such as flood control or MOP (minimum operation level) requirements are considered as constraints on either reservoir water surface elevations or storage limits, as summarized below.

3.4 Constraints

$$ {V}_i^{t+1}-{V}_i^t=\left(\left({Q}_{in,i}^t+{Q}_{in,i}^{t+1}\right)/2-\left({Q}_{out,i}^t+{Q}_{out,i}^{t+1}\right)/2\right)\cdot \Delta t $$
(4)
$$ {H}_{r\min, i}\le {H}_{r,i}^t\le {H}_{r\mathrm{m} ax,i} $$
(5)
$$ {QS}_t^i={QF}_t^i $$
(6)
$$ {MOP}_{low}^i\le {H}_{r,i}^i\le {MOP}_{up}^i $$
(7)
$$ {Q}_{tb\_\min, i}\le {Q}_{tb,i}^t\le {Q}_{tb\_\max, i} $$
(8)
$$ \left|{Q}_{out,i}^t-{Q}_{out,i}^{t+1}\right|\le {Q}_{out\_ ramp\_ allow,i}^t $$
(9)
$$ {H}_{r,i}^t-{H}_{r,i}^{t+1}\le {H}_{ramp\_ down,i}^t $$
(10)
$$ {TW}_{r,i}^t-{TW}_{r,i}^{t+1}\le {TW}_{ramp\_ down,i}^t $$
(11)
$$ {N}_{d\_\min, i}\le {N}_{d,i}^t\le {N}_{d\_\max, i} $$
(12)

where V is reservoir storage; Qin and Qout are inflow to and outflow from reservoirs, respectively; ∆t is time step; Hr is forebay elevation or reservoir water surface elevation; Hrmin and Hrmax are allowed minimum and maximum forebay elevations, respectively; QS is spill flow and QF is fish flow requirement; MOPlow and MOPup are lower and upper boundary for the MOP requirement on forebay elevation, respectively. Qtb is turbine flow, Qtb_min and Qtb_max are minimum and maximum allowed turbine flows, respectively; Qout_ramp_allow is allowed ramping rate for the outflow between any two consecutive time steps; Hramp_down is allowed ramping rate when reservoir water level is decreasing; TWramp_down is allowed ramping rate for tailwater when tailwater level is decreasing; Nd is power output, Nd_min is minimum output requirement, and Nd_max is maximum output capacity. The number of constraints is approximately 28,000 and many of them are highly nonlinear resulting in a complex search space.

3.5 Robust Formulation

The problem is formulated as a robust optimization (RO) that accounts for uncertainty. The RO basically seeks for an optimal decision on the worst case scenario and the so-called robustness can be adjusted by reflecting DM’s preference on the risk attitude towards uncertainty. In this formulation, we treat the optimization as a minimization problem with a weighted sum of the mean and standard deviation, in which the relative weighting is determined by the risk tolerance coefficient θ. This formulation can be written as

$$ \min \left({\mu}_i+\theta \bullet {\sigma}_i\right) $$
(13)

where i (=1, 2) represent the two objectives; μ and σ are mean and standard deviation of each objective, respectively. The risk tolerance coefficient θ is provided by the DM or alternatively derived by using utility theory, in which the risk attitude of the DM are modelled via a utility function. For simplicity, θ is set to 0.5, which is a balanced attitude of the DM.

Regarding the handling of constraints, the “hard” constraint approach is used herein where no constraint violation is allowed for any realization of the data in the uncertainty set.

3.6 Model Configuration

The optimization experiments were conducted using NSGA-II only, MADS only and a hybrid model where the MADS was implemented one, two, five and ten times during the global optimization. This resulted in a total of six experiments. The population for all experiments was the same and was set to 50. It is noted that larger populations normally result in better performance but lead to a heavier computational cost. The stopping criteria for the NSGA-II only and hybrid models are the number of generations, which was set to 4000. The stopping criteria for the MADS only was set to be when the objective difference is smaller than 10−3. Because of the random nature of GA, in a similar way to other random-based search algorithms, optimization results may vary for different runs, especially for problems with complex search space and multiple local optima. To provide a fair comparison, the initial population for all experiments were set to be the same. We first ran the experiment with the NSGA-II only and recorded the first population (i.e. solutions that are randomly generated). This recorded information was then used as the first population for the other experiments. For the experiments with the hybrid model, the NSGA-II was run for the first 1000 generations and then the MADS was started at regular intervals between the 1000th and 3000th generations. For example, the hybrid model with 2 times of MADS would start the MADS at the 1000th and 3000th generations, respectively. After the 3000th generation, the optimization continued with the NSGA-II and stopped at the 4000th generation.

The solutions of the objective functions at every ten generations were recorded for the experiments with NSGA-II only and for those using the hybrid model. Each of these solutions contain 50 points (population is 50) and form a Pareto front in the two-dimensional objective space.

4 Results and Discussion

The resulting Pareto front at every ten generations are shown in Fig. 3. As can be observed in Fig. 3, the solutions using NSGA-II only gradually move from the left-upper region to the right-lower region, where the values of the objective functions are improved. This means that power deficit to the demand is decreased and extra power for heavy load hours is increased, which results are desirable for the decision maker. The extension of the solutions is also gradually increased as diversity is gained in the process. However, the extension increase may not be significant or even may decrease depending on the structure of feasible regions in the search space and the ability of the algorithm for maintaining diversity. For the experiments with the hybrid model, the optimization evolution was found to present clear gaps in the objective space as greater convergence was gained from the MADS process. Overall, it is observed that a larger number of MADS implementation leads to a better convergence; however, the diversity of the solutions are decreased. The later means that the two objectives of the reservoir operation problem (i.e., power deficit to the demand and extra power for heavy load hours) are both improved but the number of options for decision-making is reduced.

Fig. 3
figure 3

Optimization evolution in the objective space for the experiments with NSGA-II only and those with the hybrid model

Full size image

The hypervolume index (Zitzler et al. 2003) of the solutions is investigated for a more quantitative comparison. A higher value of the hypervolume index indicates better quality of the solution in terms of convergence and diversity. Fig. 4 shows the hypervolume index at every ten generations for the experiment with NSGA-II only and those of the hybrid model. The improvement of the hypervolume index at early stages (e.g. first 1000 generations in Fig. 4) is very similar for all five experiments. This is likely because the same initial population is used for all of these experiments. In a similar fashion to the first 1000 generations, the experiment with NSGA-II only resulted in a continuous increase of the hypervolume index during the last 3000 generations as the diversity and convergence of the solutions were gradually improved (see Fig. 3). In contrast to the results with the NSGA-II only, the hypervolume index for all hybrid optimizations show sudden jumps after the implementation of the MADS. The results also show that a larger number of hybridization times (e.g., number of times MADS is implemented) gives a higher hypervolume index, which indicates a better quality of the solution in terms of convergence and diversity. For better visualization, the optimal solutions of the last generation are shown in Fig. 5. This figure also shows a reference solution, which was obtained with the NSGA-II only using 100,000 generations. This reference solution represent the best possible results that can be achieved for the two objectives in the reservoir operation optimization problem (i.e., minimize the power deficit to the demand and maximize extra power for heavy load hours). As the two objectives are conflicting with each other, without additional subjective preference information, all solutions from the reference Pareto are considered equally good in the context of multi-objective optimization and selection of one solution depends on preference of the decision maker. The solutions for the experiment with MADS only are also included for comparison. Fig. 5 shows the final optimal solutions in objective space for all experiments. The result for the experiment with MADS only is inferior to the other experiments. This is because the MADS, which focus is on convergence, may be trapped into local optima. Contrary to the MADS, diversity is created by the NSGA-II. It is worth mentioning that too many local exploitation decreases the diversity of the solutions in the process of seeking for convergence. The optimal solutions for the hybrid model with ten hybridization times is the closest to the reference solution. However, the diversity of the solutions is decreased compared to the hybrid model with lesser hybridization times.

Fig. 4
figure 4

Run-time hypervolume index for NSGA-II and the hybrid model

Full size image
Fig. 5
figure 5

Final optimal solutions in objective space for all experiments

Full size image

Another important aspect of the algorithm is the computational cost. The computational cost of the NSGA-II can be evaluated based on the number of generations or function evaluations. However, this approach is not applicable to the MADS because this method takes the objective difference as the stopping criteria. For a fair comparison, the central processing unit (CPU) time was recorded for all experiments under the same computing environment. The computational cost is expressed as a dimensionless ratio denoted as computational index, where the CPU time of the experiment with NSGA-II only is used as the benchmark (e.g., ratio denominator). The result of the computational index is shown in Fig. 6. The final hypervolume index for all experiments is also included for comparison. The results for experiment 1 (NSGA-II only) and 2 (one hybridization) in Fig. 6 are used to produce a straight line (dashed line) as a representation of linear relationship. As shown in Fig. 6, the hypervolume index increases almost linearly until the number of hybridization times is about 2. For a larger number of hybridization times, the hypervolume index still increases, but at a much slower rate. The computational cost also increases with the number of hybridization times. For instance, for ten hybridization times, the computational cost is increased by 30% compared to the case with no hybridization. Also, as shown in Fig. 6, the computational cost for the experiment with the MADS only is the lowest, but its hypervolume index is also the lowest. The hybrid model with two hybridization times shows overall good performance in terms of hypervolume index, diversity of solutions and computational cost. For two hybridization times, the hypervolume index is improved by nearly 10% at an increase of computational cost of less than 0.1% compared to the NSGA-II.

Fig. 6
figure 6

Hypervolume index of final solutions and their associated computational costs for the six experiments

Full size image

5 Conclusion

A novel hybrid optimization model, which incorporates the MADS into the NSGA-II, is developed to enhance local search in global exploration of the NSGA-II. An achievement scalarizing function is introduced in the MADS to attain Pareto optimal solutions. The major advantages of the model are (1) derivative-free, (2) fast convergence and (3) efficient exchange of solution vectors between local and global optimization methods. The case study for the optimization experiments is the short-term operation of a multi-objective reservoir system under uncertainty. In general, the results show that the hybrid model has a superior performance compared to both NSGA-II only and MADS only. The hybrid model with two times of MADS shows overall good performance in terms of hypervolume index, solution diversity and computational cost. For this case, the hypervolume index is improved by nearly 10% at an increase of computational cost of less than 0.1%, compared to the NSGA-II only model. Overall, the proposed hybrid model is derivative-free and can be applied to a wide array of complex optimization problems in water resource planning and management.