1 Introduction

Seawater intrusion (SWI) is generally characterized by quantitative indicators, which include the external metrics that delineate the outward boundary of the saline plume and the freshwater-saltwater interface, outlining the wedge-like shape of the plume. Incorrect management of freshwater pumping may eventually lead to the salinization of pumping wells, which would occur following the mixing of only 250 mg/l of chloride after which freshwater is considered undrinkable as per WHO regulations (WHO 2011), which is equivalent to less than 1% of seawater. Mixing with 6% of seawater is sufficient to render groundwater unsuitable for all purposes except for cooling (Morris et al. 2003).

As saline water intrudes deeper into the aquifer and approaches the location of the pumping wells, large withdrawal of groundwater leads to the rise of the freshwater-saltwater interface below or within the vicinity of the well, a process known as saltwater upconing mechanism (Reilly and Goodman 1987). Groundwater pumping is considered one of the most important challenges that promotes SWI (Werner et al. 2013), and was therefore addressed in many investigations. Ferguson and Gleeson (2012) shows that coastal aquifers are more vulnerable to wells extraction than the predicted sea level rise.

Few studies investigated the upconing mechanism within 2D laboratory-scale experiments (e.g. Mehdizadeh et al. 2015; Noorabadi et al. 2017). In most of the previous upconing laboratory studies, the variation of salt concentration within the freshwater-saltwater transition zone during the upconing was not explored mostly because measurements were only through visual observations. Thus, crucial details of transient related phenomena occurring within the freshwater-saltwater transition zone were poorly described.

Several numerical studies have attempted to explore the upconing problem in field and laboratory scale models (e.g. Diersch et al. 1984; Reilly and Goodman 1987; Jakovovic et al. 2011; Garabedian 2013). Diersch et al. (1984) investigated the saltwater upconing process using an axisymmetric model assuming steady-state condition. Their results showed the influence of dispersion and demonstrated that density and dispersion coupling induced some new effects in the breakthrough behaviour of the concentration for the pumped water. Jakovovic et al. (2011) found that the breakthrough of well salinity in the high pumping rates was controlled by the width of the plume rather than the degree of dispersiveness. Reilly and Goodman (1987) showed that longitudinal dispersion induced negligible effects on the concentration distribution, but evidenced the strong sensitivity of the upconing saltwater distribution to transverse dispersivity.

Few researches recently simulated the upconing phenomena based on field data (Llopis-Albert and Pulido-Velazquez 2014, 2015; Mehdizadeh et al. 2015; Strack et al. 2016; De Filippis et al. 2016; Jakovovic et al. 2016). It could be concluded from these studies that the applicability of the sharp-interface approach in field-scale strongly depends on well location and pumping rate.

Reilly and Goodman (1987) defined the critical pumping rate as the highest rate at which the freshwater-saltwater interface can remain stable below the well without the well discharge being rendered saline. Only limited studies have investigated the sensitivity of the critical pumping rate to the hydraulic and hydrogeological parameters of aquifers. However, most of these investigations were focused on axisymmetric models (e.g. Zhou et al. (2005) and/or only presented qualitative analysis (e.g. Mehdizadeh et al. 2015).

As per our knowledge, no previous studies explored the impact of hydrogeological parameters on saltwater upconing behaviour in coastal aquifers considering inclined freshwater-saltwater interface, which is more realistic than the widely used axisymmetric models as it allows natural horizontal motion of saline water. The main purpose of this study is therefore to examine the sensitivity of saltwater upconing characteristic (shape and location) to the main hydrogeological parameters and well location. Experiments were conducted in laboratory-scale aquifer with inclined interface where automated image analysis technique was used to provide high spatial and temporal resolution of the saline wedge. The SEAWAT model was used to assess the consistency of the experimental results with the numerical predictions. In contrast to most of previous studies that only used a qualitative comparison of the saltwater wedge at steady state, this study used both qualitative analysis (shape of the wedge) and quantitative analysis (transient toe length). The numerical model was thereafter used to explore the sensitivity of the critical pumping rate (defined here as the rate at which the 1% salt concentration reaches the well) and the critical time (the time needed for the saltwater to reach the well) to the well design parameters (pumping rates, depth and location) and the main aquifer properties (hydraulic conductivity, dispersivity and saltwater density).

2 Methodology

2.1 Experimental Method

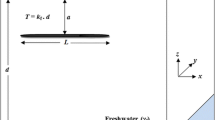
A laboratory flow tank of dimensions 0.38 m ×0.15 m ×0.01 m was used for the experiments. The tank was composed of a central chamber flanked by two side reservoirs (Fig. 1). The central chamber was filled with 1090 μm clear glass beads to simulate a homogeneous porous media. The hydraulic conductivity of the porous media (85 cm/min) was estimated using in situ measurement within the flow tank (Abdoulhalik et al. 2017; Abdoulhalik and Ahmed 2017). LED lights (Camtree 600) were placed behind the experimental setup to illuminate the porous media and a light diffuser was fixed to the back of the tank to ensure homogeneity of the light throughout the aquifer. A high speed camera IDT MotionPro X-Series with a resolution of 1280 × 1024 pixels and an 8-bit grayscale pixel depth was used to capture images of the experiments. The light intensity was then transformed into salt concentrations. More details about the experimental methodology could be found in Robinson et al. (2015).

Fig. 1
figure 1

Photograph of the experimental set up; 1) porous media chamber; 2) freshwater reservoir; 3) saltwater reservoir; 4) ultrasonic sensors; 5) high speed camera; 6) LED lights

Full size image

The pumping well was simulated using a Terumo Neolus hypodermic needle connected by a flexible hose (Maprene) to a peristaltic pump Watson Marlow 101 U/R. The needle was 50 mm long with an outside and inside diameter of 1.1 mm and 0.7 mm, respectively. The internal diameter of the hose was 4.8 mm. The hose was carefully adjusted such that the tip of the needle was located 85 mm above the bottom of the tank, and 190 mm away from the seaside boundary. The needle was kept at the same position in all experiments.

The investigation included three experiments, each of them lasted within 50 min. In the first experiment, the saline wedge was allowed to intrude into the aquifer (head difference dh = 6 mm) and reaches steady state with no pumping. In the second experiment, the pump was switched on at a rate of 0.49 mL/s to facilitate the upconing mechanism. This rate was selected after trial and error and was found to enable observation of the saltwater upconing. In the third experiment, the pump was switched off, which allowed the saline wedge to recede. The saltwater concentration was fixed at 28.96 g/L, which yields a density of 1020 kg/m3. The freshwater and saltwater boundary heads were maintained at 135.7 and 129.7 mm respectively.

2.2 Numerical Model and Procedure

The MODFLOW family variable density flow code SEAWAT (Guo and Langevin 2002) was used to perform the numerical simulations. SEAWAT has been widely used for saltwater intrusion numerical simulations (e.g. Abdoulhalik and Ahmed 2017; Abdoulhalik et al. 2017). Table 1 provides a summary of the numerical variables used in the simulations. The dispersivity and element dimensions provided numerical stability by satisfying the Peclet number criterion (Voss and Provost 2010). A freshwater (C = 0 g/L) hydrostatic boundary condition was forced on the left side boundary and a hydrostatic saltwater (C = 28.96 g/L) boundary condition was applied on the right side boundary. The time step of the simulations was set to 0.5 min.

Table 1 Summary of the numerical parameters
Full size table

Three stress periods were used similar to those of the laboratory experiments. At the initial condition, the model domain corresponded to an entirely fresh aquifer. The first stress period was used to set the first steady state condition, whereby the freshwater and saltwater boundary were set at 135.7 mm and 129.7 mm, respectively, allowing penetration of saline water into a fully fresh model domain. Once the initial steady state was reached, the abstraction was simulated as a well at the specified location with a discharge rate set at 0.49 mL/s for 50 min for the system to reach quasi steady state condition. The last stress period was dedicated for the retreat of the saltwater water wedge, following the interruption of the pumping. Table 1 shows a summary of the parameters used in the numerical simulations.

3 Results and Discussion

3.1 Saltwater Upconing Experiment

Figure 2 shows the concentration colour maps of the saltwater wedges at initial condition and upconing stage. The steady state condition was assumed when no changes in the toe length and the shape of the saltwater wedge could be observed. Following the drop of the freshwater level down to 135.7 mm, thereby imposing a head difference of dh = 6 mm, the saline water was allowed to enter the aquifer system and intrude inland until it reached steady state condition (Fig. 2a). The initiation of the abstraction subsequently induced further landward and upward penetration of the saline water into the system until it eventually intercepted the bore of the well. The final stage of the upconing was reached within 50 min after turning on the pump (Fig. 2b). The percentage of increase in the toe length caused by the abstraction was about 71%. It is interesting to note a significantly wider transition zone width in the upconing stage (especially in the upper part of the interface) compared to the initial condition. The receding phase was then initiated after turning off the pump. Laboratory observations showed that the tip of the cone subsequently moved rapidly away from the well towards the seaside and the freshwater-saltwater interface subsequently regained its natural relatively straight shape, similar to the initial steady state condition, since the head difference was not changed (not shown for brevity).

Fig. 2
figure 2

Steady state concentration colour maps of the (a) Initial condition. b Upconing condition

Full size image

3.2 Numerical Validation

While only qualitative analysis of the wedge shape at steady state condition were provided in most of the previous studies, the numerical validation was herein through both qualitative comparison of the shape of the transient saline plumes during the upconing mechanism and the receding phase as well as quantitative comparison of the transient toe length data. Figure 3 shows the comparison between the transient experimental and numerical saltwater wedges during the upconing process at selected time intervals until the system reached steady state condition. In overall, the numerical model was able to depict reasonably well the development of the shape of the upconing wedge observed in the physical experiment, although the numerical model predicted slightly faster landward saltwater motion. This could be observed in the visibly shorter distance between the freshwater-saltwater interface and the bore of the well in the numerical model at t = 10 min. The curved shape of the freshwater-saltwater interface commonly observed in early upconing stage was nonetheless well reproduced in the model. In both models, the saline water intercepted the bore of the well within 30 min, albeit the concentration of the abstracted saline water was visibly lower in the physical model and the transition zone was slightly wider. The steady state condition occurred within 50 min in the numerical model and the shape of the wedge matched well that visualized in the experimental concentration colour map, despite some minor discrepancies around the bore of the well, probably due to a slightly delayed steady state in the physical experiment.

Fig. 3
figure 3

Comparison between experimental and numerical saltwater upconing process (Q = 0.49 mL/s.) at different time steps from the start of pumping a Numerical images b Experimental concentration colour maps

Full size image

Figure 4 presents the comparison between the transient experimental and numerical saltwater wedges during the receding phase, i.e. after the abstraction was stopped. The results show that numerical model predicted very well the seaward motion of the saltwater wedge observed in the physical model. The model reproduced similar rapid seaward motion of the tip of the cone away from the well as well as the subsequent lowering of the freshwater-saltwater interface until it regained its natural relatively straight shape at steady state. The widening of the transition zone was also exhibited in the numerical model, although slightly narrower than the experimental model. The receding phase reached steady state relatively quicker in the numerical model at t = 15 min, while some changes could still be observed in the experimental wedge, albeit merely located within the transition zone.

Fig. 4
figure 4

Comparison between experimental and numerical saltwater receding process at different time step from the start of turning off pumps a Numerical images b Experimental concentration colour maps

Full size image

Figure 5 shows the quantitative comparison between the transient experimental and numerical toe length results. The results show that the numerical toe length data agree well with the experimental results for both the upconing and receding phases, despite the toe length was slightly overestimated in the numerical model. This mismatch might be due to possible minor source of heterogeneity commonly associated with the packing of the beads, while the numerical model assumes perfectly homogenous medium. Other factors such as tiny fluctuations in the water levels caused by the surrounding vibrations may also contribute to this minor discrepancy. In general, the results show good agreement between numerical and experimental shape of the saltwater plume and the toe length data.

Fig. 5
figure 5

Comparison between transient experimental and numerical toe length data

Full size image

4 Sensitivity Analysis

The numerical model was thereafter used to perform series of simulations in order to explore the sensitivity of the critical pumping rate (defined here as the rate at which the 1% salt concentration reaches the well) and the critical time (the time needed for the upconing saltwater to reach the well) to the well design parameters (pumping rates, depth and location) and the main aquifer properties (hydraulic conductivity, dispersivity and saltwater density) in unconfined coastal aquifer system. In all the simulations, the initial condition (prior to abstraction) corresponded to that of a steady state saltwater wedge associated with a head difference dh = 6 mm. The aquifer parameters and the well design parameters were similar to those of the physical and numerical models, which were shown in Table 1.

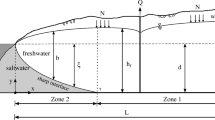
The well location was expressed by the dimensionless location ratio Lw/L, where Lw is the well distance from the coastline and L is the length of the aquifer. The well depth was expressed by the dimensionless depth ratio Z/H, where Z is the height of the well from the aquifer bottom and H is the aquifer thickness. Table 2 presents a summary of the different scenarios tested. Five different well locations and four well depths were tested. For the different locations and depths, the pumping rates were selected through trials and errors using an incremental step of 0.005 mL/s.

Table 2 Summary of the parameters tested in the sensitivity analysis
Full size table

4.1 Effect of the Pumping Rate at Different Well Locations and Depths

Figure 6 depicts the advancing rate of the upconing wedge towards the well for some selective pumping rates at three different well locations. The vertical axis in the figure, Xu, represents the horizontal distance between the upconing at 1% salt concentration and the well. Obviously, increasing the pumping rate induced faster upconing advancement rate towards the well, characterized by decreasing the Xu values. The upward movement of the saline water was much faster in the early stage of the upconing process, and slowed down as it approached the well. For each well location, the critical pumping rate corresponded to the pumping rate at which Xu = 0, i.e. the 1% salt contour line of the cone apex reached the well. For instance, for a location ratio Lw/L = 0.5 and Q = 0.36 mL/s, the steady state was reached before the upconing wedge reached the well, while for Q = 0.38 mL/s, the upconing wedge reached the well in even lesser time. A further increment of the rate to Q = 0.4 mL/s caused faster salinization of the well. That is because when the freshwater extraction was initiated, the pressure exerted by freshwater on the interface was reduced, which allowed rapid upward motion of the saline water. This upward motion was then slowed down as the saline water reached the vicinity of the well. When the steady state was reached before the saline water reaches the well, the seaward freshwater flow and the density contrast effects act jointly to stabilize the saltwater wedge.

Fig. 6
figure 6

Effect of pumping rate on the movement of the upconing wedge

Full size image

The critical pumping rate varied with the well location and depth, which is expected (Fig. 7a). The closer the well was located to the initial saltwater wedge position, the lower was the critical pumping rate, which would imply a faster salinization of the well. The critical pumping rate was more sensitive to the variations of the location than to the depth of the well. The farther the well was located from the seaside, the longer was the distance to be travelled horizontally by the saltwater, with the seaward freshwater flow slowing down its motion. At fixed depth, the motion of saline water toward the well was mainly vertical, while most of the flow along the upper part of the interface was reduced because of the abstraction.

Fig. 7
figure 7

Effect of varying well location and depth ratios (a) on the critical pumping rate and (b) on the critical time

Full size image

Similarly, the impact of changing the well location had more influence on the critical time than changing the depth (Fig. 7b). The distance from the coastline is an important parameter to be considered when planning the maximum permissible pumping rate. Interestingly, the critical time increases almost linearly with increasing location and depth ratios following a relatively simple linear equation of type tc = aX+ b, with a and b being the linear regression coefficients and X being either the Lw/L or Z/H ratio. The values of a and b for the current system are shown in the figure. The strong linearity of the correlations is evidenced by the relatively high coefficient of determination (R2 > 0.99).

4.2 Effect of the Hydraulic Conductivity

In this section, the pumping rate was gradually increased by an increment of 0.005 mL/s for five values of hydraulic conductivity within the range 36–108 cm/min. This was done for three different well locations (with fixed depth) and three different well depths (at fixed location), as shown in Fig. 8.

Fig. 8
figure 8

Impact of the hydraulic conductivity on (a) the critical pumping rate (b) the critical time. In Fig. 8b, the critical pumping of K = 85 cm/min was used, and K ranged from 36 to 85 cm/min

Full size image

The critical pumping rate was very sensitive to the hydraulic conductivity (Fig. 8a). For all the well configuration tested, the lowest critical pumping rate was found for the lowest hydraulic conductivity, which reflects the vulnerability of low permeability aquifers to saltwater upconing process and thus to well salinization. This may be because the freshwater flow contributing in the seaward repulsion of the saltwater wedge would be reduced as the hydraulic conductivity of the aquifer system is lowered, thus the horizontal and vertical migration of the saltwater wedge caused by the abstraction would subsequently be facilitated.

For all the well locations tested, the critical time also decreased with decreasing the hydraulic conductivity (Fig. 8b). In these simulations, the critical pumping rates of the base case K = 85 cm/min was applied to the other hydraulic conductivity values to ensure that the upconing wedge reached the well in all cases. Results suggest the sensitivity of the critical time to hydraulic conductivity was more significant for wells located farther away from the initial interface position.

4.3 Effect of the Saltwater Density

The sensitivity of the critical pumping rate to the saltwater density was explored for three different saltwater densities, namely 1020, 1025, and 1030 kg/m3. This was performed for three different well depth ratios Z/H = 0.5, 0.625 and 0.75 and for a fixed well location.

Increasing the saltwater density induced a smaller critical pumping rate (Fig. 9a). This means that for denser saltwater, the upconing occurs at lower pumping rate. By contrast, lighter saltwater density induced greater critical pumping rate. These results show that for the well configurations considered here, higher saltwater densities would tend to facilitate the saltwater upconing mechanism. This is probably because for denser saltwater, the density contrast effects are greater, which enforces the lateral motion of the saltwater wedge in the early stage of the upconing. The results also showed that for a fixed saltwater density, the critical pumping rate decreased with increasing well depth, as expected.

Fig. 9
figure 9

Effect of the saltwater density on (a) the critical pumping rate, and (b) the critical time

Full size image

Figure 9b, shows the density effect on the critical time for two different location ratios (Lw/L = 0.5 and 0.25) and the three different depth ratios. In this scenario, the critical pumping rate applied was that of the case ρ = 1020 kg/m3 to ensure that the upconing wedge could reach the well in all other cases. The influence of the saltwater density on the critical time was more significant for wells located farther away from the initial position of the interface. In such case, for ρ = 1020 kg/m3 and Lw/L = 0.5, the critical time was relatively high for all well depths, but decreased substantially as the density increased to 1030 kg/m3, where the critical time became nearly twice smaller. This difference was less pronounced in the case where the well was closer (Lw/L = 0.25). This is because in the case where the well was farther away from the initial location of the interface, the horizontal motion of the saltwater wedge preceding the upconing mechanism was significantly faster for higher density values, thus subsequently reduces the critical time. By contrast, when the well was located closer to the initial position of the interface, this horizontal motion was limited since the motion of the saline water in such case was mostly vertical, thus the impact of the density change on the critical time was less pronounced.

4.4 Effect of the Dispersivity

The sensitivity of the upconing mechanism to dispersivity was explored to understand the contribution of dispersivity to well salinization. Increasing the dispersivity only induced very slight decrease of the critical pumping rate, albeit was more visible when decreasing the transversal dispersivity and the critical time decreased with increasing dispersivity. This could be because high dispersivity induces more mixing along the interface which would lead to subsequent widening of the transition zone. In such conditions, less time would be required for the low concentration isoline of the dispersive zone to reach the well. Thus, for equivalent pumping rate, these results suggest that higher dispersive systems would tend to induce faster upconing mechanism.

5 Summary and Conclusions

For the first time, this study provides a thorough quantitative analysis on the impact of the key factors influencing the upconing shape and location in an unconfined coastal aquifer model. The numerical model was first compared with transient laboratory experiments where automated image analysis technique was used. The experiment investigated three stages, namely the initial stage (no pumping), the upconing stage, and the receding stage after cease of pumping. The SEAWAT code was used for the numerical simulations. In contrast to most of the previous studies where only qualitative comparison of the wedge at steady state condition was provided, the validation of the numerical model was herein though qualitative comparison of the shape of the wedge under transient conditions and quantitative comparison of the transient toe length data in both upconing and receding phases. In both the experimental and numerical models, the saline water intercepted the bore of the well within 30 min, albeit the concentration of the abstracted saline water was visibly lower in the physical model and the transition zone was slightly wider.

The resulting model was used to perform additional simulations to explore the sensitivity of the critical pumping rate and the critical time to the design parameters of the well and the main hydrogeological parameters in an unconfined aquifer model. The results show that the critical pumping rate and the critical time were more sensitive to the variations in the well location than the well depth. The critical time increased with increasing the well location and depth ratios following relatively simple linear equation. For all configurations tested, the lowest critical pumping rate was found for the lowest hydraulic conductivity, which reflects the vulnerability of low permeability aquifers to salinization because of freshwater extractions. In addition, higher saltwater densities facilitated the saltwater upconing mechanism. The influence of the saltwater density on the critical time was more significant for wells located farther away from the initial position of the interface. The results show that increasing the dispersivity only induced very little change on the critical pumping rate. For a fixed pumping rate, the critical time decreased with increasing dispersivity, which suggests that higher dispersive systems would tend to induce faster upconing mechanism.