1 Introduction

Runoff plots have been an important means to monitor runoff and soil loss since their development by the German scientist Wollny in 1882 (Baver 1938). Peak flow is a key parameter when selecting the size of the trough connecting a runoff plot and a collecting tank and/or the size of the H-flume or other equipment used to measure the flow discharge of runoff plots. On the other hand, the design of soil-conservation measures, including terraces, fish-scale ditches and road or highway gutters, also requires knowledge of the peak flow from small drainage areas. In addition, peak flow rate is an important parameter in the modified universal soil loss equation (MUSLE) (Williams 1975) which to calculate the soil loss from upland slope. The MUSLE is also a significant part in soil and water assessment tool (SWAT) (Neitsch et al. 2005) which has been widely used all over the world. Thus, the precise prediction of peak flow is important when small drainage areas are involved.

In 1851, Mulvaney presented the Rational Formula (eq. (1)), which may have been the first equation for predicting peak flow (Chow 1964):

$$ {Q}_p=\frac{CIA}{360} $$
(1)

where Q p is the peak flow (m3 s−1), C is a runoff coefficient, I is the rainfall intensity at the time of concentration (mm/h), and A is the drainage area (ha). O’Connell (1868) linked peak discharge to drainage area and proposed the following power law formula:

$$ {Q}_{\mathrm{p}}=\mathrm{a}{A}^{0.5} $$
(2)

where a is a coefficient related to the region. Creager et al. (1944) concluded that the exponent of A was not constant and instead decreased as the drainage area increased. They proposed the following formula:

$$ {Q}_{\mathrm{p}}=46{CA}^{0.894{A}^{-0.048}} $$
(3)

Where C = 200. Then, in the early 1960s, the United States Geological Survey (USGS) adopted the form of eq. (2) and rewrote it as eq. (4) to predict peak flow for a given return period (Ayalew et al. 2014):

$$ {Q}_p=\alpha {A}^{\theta} $$
(4)

where α and θ are functions of a return period. The value of exponent θ is dependent on the watershed scale. Subsequently, many studies were performed to determine the value of θ. The θ value obtained by Benson (1962) was 0.85 for a return period of 2.33 yr. at 164 watersheds (2.5–26,000 km2) in the humid New England region. Later, Benson (1964) used data from semi-arid regions of Texas and New Mexico and found that θ was 0.59 for a return period of 2.33 yr. at 219 watersheds (2.5–91,000 km2). Alexander (1972) obtained an average estimate of 0.7 for θ using data from U.S. and British catchments with drainage areas that varied from 130 km2 to 5200 km2. Murphey et al. (1977) found a mean θ value of 0.62 using data from 149 events and 11 watersheds in Walnut Gulch, Arizona, U.S. Goodrich et al. (1997) also used data collected in the Walnut Gulch watershed and found that θ was 0.85 for 2-yr. return periods and drainage areas less than 1 km2 but 0.55 for 2-yr. return periods and drainage areas exceeding 1 km2. Ogden and Dawdy (2003) analyzed peak discharge data from the Goodwin Creek basin, Mississippi, U.S. They examined 16 yr. of continuous rainfall and runoff data for drainage areas ranging from 0.172 to 21.2 km2 and found a θ value of 0.77, independent of the return period. Gupta et al. (2007) determined that θ was 1 for small basins dominated by rainfall–runoff variability and 0.5 for large basins dominated by network structure and flow dynamics. Gupta et al. (2010) used mean annual peak flow data for the Iowa River basin (6.6 km2 to 32,374 km2) and obtained a θ value of 0.54. Di Lazzaro and Volpi (2011) determined a θ value of 0.52 using data for a watershed area located in the Tiber River region, Central Italy, that varied from 218 km2 to 4116 km2.

In addition, several empirical equations were developed. Knisel (1980) derived a peak flow equation that included the variables of drainage area, runoff depth, channel slope and watershed length and width. The exponent of the drainage area was 0.7 for watershed areas ranging from 0.71 to 62.18 km2. Fu et al. (2008) used drainage area, runoff depth and rainfall depth as variables and obtained a drainage area exponent of 0.59.

Based on these results, we can observe that θ -varies with watershed area. The values of the drainage area exponents in the cited studies are summarized in Table 1, which shows that the exponent of the drainage area decreases generally with increased drainage area, which was in agreement with the results of Creager et al. (1944) and Alexander (1972). The existing peak flow equations are primarily derived from the data on the watershed scale. The smallest drainage area used in the literature is 1830 m2 (Table 1). Little information on the peak flow rate equation is available for the plot scale (40.5 m2 for unit plot which was tipical size for runoff plot) or small drainage area, and no study has investigated whether the peak flow equation developed for the watershed scale is suitable for the plot scale. Therefore, the purpose of this study is to validate the suitability of watershed peak flow equations for the plot scale and to develop a new peak flow rate equation for this scale. This study will provide new knowledge for peak flow in small area, which could be helpful for understanding the mechanism of peak flow generation and development. The new equations also can be used in design of the conservation practices and runoff and soil loss measure devices.

Table 1 Exponent values of the drainage area in the peak flow equations
Full size table

2 Materials and Methods

2.1 Data Sources

In this study, measured peak flow data for 5 runoff plots and 5 watersheds were used. The runoff plot data were used to develop new peak flow equations for small-scale drainage areas. The data for 5 watersheds were used to validate the existing equations and to determine whether they performed the same or differently on the watershed and plot scales.

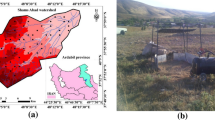
The runoff plots are located in the Tuanshangou catchment in the center of the Loess Plateau in Zizhou county, Shaanxi province, China (Fig.1). The plot areas varied from 300 m2 to 17,200 m2 (Table 2). Three plots (Nos. 2, 3 and 4) were regular rectangles with a width of 15 m and different slope lengths. One plot (No. 7) covered an entire hill slope from the top of the hill to the bottom of the valley. The last plot (No. 9) was a small catchment. The slope steepness of the five plots changed from 40.4% to 67.5%, and the slope aspect was mainly northeast. The soil type was Cultivated Loessial Soils, which is characterized by a uniform texture and weak structure (Li et al. 2003). The land use of all the plots was cropland, and they were regularly cultivated. The region has a semiarid continental climate with an average annual rainfall of 535 mm. Rainfall events primarily occur from June to September. A total of 149 storm events with runoff depths exceeding 0.1 mm for the period 1963–1967 were selected. The runoff depth varied from 0.1 mm to 28.67 mm (Fig. 2). The runoff duration is generally short and less than 215 min (Table 3). The maximum runoff duration significantly increases as the plot area increases. The measured peak flow rates ranged from 0.2 ls−1 to 919 ls−1. The magnitude of the peak flow rate varied with the plot area (Fig. 3). The peak flow rates for drainage areas of 0.03, 0.06, 0.09, 0.49 and 1.72 ha at a cumulative frequency of approximately 50% (i.e., a 2-yr. return period) were 5, 10, 15, 50 and 100 l/s, respectively. Most runoff hydrographs exhibit one peak value and positive skewness (Fig. 4), indicating that the discharge rises rapidly after the runoff begins and then declines slowly.

Fig. 1
figure 1

Location of plots and watersheds used in this study

Full size image
Table 2 Runoff plot area and peak flow rate used in this study
Full size table
Fig. 2
figure 2

Histogram and cumulative frequency of the runoff depth

Full size image
Table 3 Quantile statistics for runoff duration (min)
Full size table
Fig. 3
figure 3

Histogram and cumulative frequency of the peak flow rate

Full size image
Fig. 4
figure 4

Flow hydrographs for certain storms

Full size image

The basic watershed information is summarized in Table 4. The watersheds are also located in Zizhou county, Shaanxi province, China (Fig.1). The climates and soil types of the watersheds resemble those of the runoff plots. The measured peak flow rates ranged from 0.002 m3 s−1 to 1520 m3 s−1.

Table 4 Watershed characteristics and peak flow rate
Full size table

2.2 Procedure

First, two peak flow rate equations were selected. Eq. (5) was from the Chemicals, Runoff and Erosion from Agricultural Management Systems (CREAMS) model (Knisel 1980), and eq. (6) was from Fu et al. (2008).

$$ {Q}_{p=}3.79{A}^{0.7}{CS}^{0.16}{\left(\frac{R}{25.4}\right)}^{0.9{A}^{0.02}}{\left(\frac{L^2}{A}\right)}^{-0.19} $$
(5)

where Q p is the peak flow rate (m3 s−1), A is the drainage area (km2), CS is the average slope of the main channel (m/km), R is the runoff depth (mm), and L is the watershed length (km).

$$ {Q}_p=6.69{A}^{0.59}{R}^{1.15{A}^{0.06}}{P}^{-0.72} $$
(6)

where P is the rainfall amount (mm).

The primary reason for selecting these equations was that the equations’ parameters are straightforward to obtain. In addition, eq. (5) had a similar size scale, and eq. (6) had climate, land use, landform and soil conditions similar to those used in this study.

Second, the Pearson correlation analysis between peak flow rate and effect factors (including plot area, runoff depth, rainfall depth, maximum 30-min rainfall intensity (I 30), plot slope steepness and length-width ratio) was conducted using SPSS 19.0 software.

Third, dimensionless analysis was conducted according to Buckingham’s π theorem. Then, regression analyses were performed to develop new equations. The runoff plot data were divided into two sets to develop and validate the equations. The first 119 events were used to develop a new equation for the plot peak flow rate. The second 30 events were used to validate the new equation. The second dataset of 30 events was obtained by selecting 1 of every 4 events in chronological order.

Finally, the following criteria were used to evaluate the equations’ performance. Model efficiency (ME) (eq.(7)) and mean absolute error (MAE) (eq.(8)) were applied to evaluate the goodness of fit between predicted and measured data.

$$ ME=1-\frac{\sum_{i=1}^n{\left({Q}_{obs}-{Q}_{cal}\right)}^2}{\sum_{i=1}^n{\left({Q}_{obs}-{\overline{Q}}_{obs}\right)}^2} $$
(7)
$$ MAE=\frac{1}{n}\sum_1^n\left|{Q}_{obs}-{Q}_{cal}\right| $$
(8)

where Q obs is the measured peak flow, Q cal is the predicted value, \( {\overline{Q}}_{obs} \) is the mean observed peak flow value, and n is the number of events.

3 Results

3.1 Validation of the Existing Peak Flow Equations

The ME of the peak flow eq. (5) in the CREAMS model ranges from 0.55 to 0.78 for different plots and from −0.35 to 0.22 for different watersheds (Table 5). The ME of eq. (5) sharply decreases when the area exceeds 1.72 ha. The ME of eq. (6) from Fu et al. (2008) varies from −4.3 to 0.83 for different plots and from 0.70 to 0.89 for different watersheds and substantially increases when the area exceeds 1.72 ha. These results indicate that the peak flow equation in the CREAMS model provides better estimation accuracy for the plot scale but worse prediction for the watershed scale. In contrast, eq. (6) has worse prediction accuracy for the plot scale but more accurate estimation for the watershed scale. The MAEs for eq. (5) and (6) are similar to the ME (Table 5).

Table 5 ME and errors of the two equations for plots and watersheds
Full size table

3.2 Development of New Equations

The peak flow rate (Q p ) was significantly correlated with plot area (A), slope steepness (S), runoff depth (R), rainfall depth (P) and maximum 30-min rainfall intensity (I 30) at the 0.01 confidence level (Table 6). Thus, we conclude that the following relationship (eq. (9)) can be used to express the peak flow rate:

$$ {Q}_p=\mathrm{f}\left( A, R, P,{I}_{30}, S\right) $$
(9)
Table 6 Pearson correlation coefficient between the peak flow and the other effect factors
Full size table

where I 30 is the maximum 30-min rainfall intensity (mm/h), and S is the slope steepness (m/m).

Dimensionless analyses were conducted based on the correlation analysis results. The runoff depth and I 30 were selected as the independent variables. According to Buckingham’s π theorem, the final result of the dimensional analysis can be expressed as the following function:

$$ \frac{Q_p}{R^2{I}_{30}}=\mathrm{f}\left(\frac{P}{R},\frac{A}{R^2}, S\right) $$
(10)

Based on eq. (10), a linear regression analysis was conducted according to the following equation:

$$ \log \left(\frac{Q_p}{R^2{I}_{30}}\right)={a}_1\mathit{\log}\left(\frac{P}{R}\right)+{a}_2\mathit{\log}\left(\frac{A}{R^2}\right)+{a}_3 logS+{a}_4+\varepsilon $$
(11)

where a1, …, a4 are regression coefficients.

In addition, the plot area, I 30 and runoff depth are straightforward to obtain and exert important effects on the peak flow rate. Thus, the linear regression analyses according to eq. (12) and (13) were also conducted.

$$ {\mathrm{logQ}}_p={a}_1 logA+{a}_2 logR+{a}_3+\varepsilon $$
(12)
$$ {\mathrm{logQ}}_p={a}_4 logA+{a}_5{logI}_{30}+{a}_6+\varepsilon $$
(13)

where a1, a2, …, and a6 are regression coefficients.

The following regression results were obtained:

$$ \log \left(\frac{Q_p}{R^2{I}_{30}}\right)=-0.846\mathit{\log}\left(\frac{P}{R}\right)+1.035\mathit{\log}\left(\frac{A}{R^2}\right)-0.899 logS-6.176{\kern1em \mathrm{adjR}}^2=0.974 $$
(14)
$$ {\mathrm{logQ}}_p=0.887 logA+0.846 logR-5.091{\kern1em \mathrm{adjR}}^2=0.951 $$
(15)
$$ {\mathrm{logQ}}_p=0.781 logA+1.486{logI}_{30}-6.469{\kern1em \mathrm{adjR}}^2=0.790 $$
(16)

The F-tests indicate that the eqs. (14), (15) and (16) were acceptable at the 0.001 confidence level. But, the adjusted R2 from eq. (16) was obviously lower than those from eq. (14) and (15). It shows that the combination of plot area and I 30 was not the best variables to predict the peak flow rate. The P-P plots of the standard residuals for eqs. (14) and (15) reveal that the residual was approximately normally distributed with a mean of zero (Fig. 5). No trend exists between peak flow and the residuals. Thus, eqs. (14) and (15) can be used to predict the peak flow rate. To simplify the equations, eqs. (14) and (15) can be rewritten as eqs. (17) and (18), respectively:

$$ \mathrm{Qp}={10}^{-6.176}{A}^{1.035}{R}^{0.777}{P}^{-0.846}{I}_{30}{S}^{-0.899} $$
(17)
$$ \mathrm{Qp}={10}^{-5.091}{A}^{0.887}{R}^{0.846} $$
(18)
Fig. 5
figure 5

P-P plots for standard residuals: (a) eq. (14) and (b) eq. (15)

Full size image

The MEs of eqs. (17) and (18) are clearly larger than those from Fu et al. (2008) and CREAMS (Table 7). MAEs of eqs. (17) and (18) are lower than those from Fu et al. (2008) and CREAMS. The peak flow rate predicted using eq. (17) and (18) tends to be evenly distributed on either side of the one-to-one line (Fig. 6). However, eq. (5) from Fu et al. (2008) and eq. (6) from the CREAMS model overestimate the peak flow rate, especially for low peak flow rates. These results indicate that eqs. (17) and (18) provide better prediction accuracy than those of Fu et al. (2008) and the CREAMS model for the plot scale.

Table 7 ME and errors of the new equations compared with previously reported equations
Full size table
Fig. 6
figure 6

Measured versus predicted peak flow rates for the modeling dataset

Full size image

3.3 Validation of the New Equations

The 30 peak flow events that were not used to develop the equations were employed to validate them. Eqs. (17) and (18) exhibited high ME values: 0.97 and 0.95, respectively. The MAE values were low (both equal to 0.01 l/s). The predicted peak flow rates were evenly distributed on either side of the one-to-one line (Fig. 7). Thus, we can conclude that these two new equations predict the peak flow rate well.

Fig. 7
figure 7

Measured versus predicted peak flow rates for the validation dataset

Full size image

4 Conclusions

The data for the runoff plots and watersheds were used to validate the peak flow rate equations of the CREAMS model and from Fu et al. (2008). The results indicated that the equation of Fu et al. (2008) was more suitable for predicting peak flow rates at the watershed scale and that the equation of the CREAMS model gave more accurate predictions at the plot scale. However, both overestimated the peak flow rate, particularly when the rate was low.

The new eqs. (17) and (18) were developed based on the results of dimensionless analysis and regression analysis. The variables of eq. (17) included drainage area, runoff depth, maximum 30-min rainfall intensity (mm/h) and slope steepness. Considering the data availability, a simpler eq. (18) was developed that only included drainage area and runoff depth. The results indicated that eqs. (17) and (18) provided good estimation accuracy with model efficiencies of 0.97 and 0.95, respectively. The MAEs of eqs. (17) and (18) were low (both equal to 0.01).

The equations developed in this study represent an important supplement to the existing peak flow rate equations. These new equations will facilitate the design of soil conservation practices and the selection of flow-observation equipment with appropriate capacity for the plot scale.