Abstract
Numerous drought indices with various intricacy have been utilised in several climatic regions. Presently, the reconnaissance drought index (RDI), which is considered as a powerful index of meteorological drought, is acquisitioning approval primarily in semi-arid and arid climatologic areas. Because RDI is based on precipitation (P) and evapotranspiration (ET), it assesses the ET estimation effects on the characterisation of drought severity computed by RDI. The current study sheds light on the impact of the ET methods, and the elevation and climate conditions on the RDI annual results, (particularly, the alpha form of the index (RDIα12)), using three of the most widespread experimental ET estimates with low data requirements. These techniques are known as Thornthwaite, Hargreaves, and Blaney-Criddle, and are utilised in addition to the Food and Agriculture Organization Penman-Monteith reference technique. Data from 24 stations for the period from 1979 to 2014 cover different elevations and climatic conditions. No significant (P > 0.05) impacts on both the standardised (RDIst) and normalised (RDIn) forms of the RDI were detected by applying the considered ET methods at various elevations for various climatic conditions. However, the RDIα12 is directly influenced with a significant (P < 0.05) deviation that has been observed by various ET methods at different elevations and climate conditions. Accordingly, consideration should be paid to the ET estimation methodologies, in particular at high elevations. The use of various approaches may lead to flaws in availability of water resources and water quality forecasts.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
One of the main water-related hazards is drought (Giannikopoulou et al. 2014), which should be considered as a three-dimensional event characterised by its severity, duration and affected area (Tsakiris and Vangelis 2005; Vangelis et al. 2013; Zarch et al. 2015). Despite the fact that there is no commonly agreed definition of the term drought, a commonly acceptable one describes the event as a considerable decline of the water availability during a lengthy time period and over a spacious region (Tigkas 2008).
For identifying, quantifying and monitoring of drought, there are different suggested methodologies. One of the most popular methods, which are distinctive collections of indicators involving meteorological, hydrological and other data, is the estimation of drought indices (Tsakiris and Vangelis 2005; Tigkas 2008; Vangelis et al. 2013; Giannikopoulou et al. 2014). Drought indices might be categorised into two main groups: the common indices and the more detailed ones. The former gives an outline of the drought event and its strength, while the latter are generally beneficial for related drought occurrences to the prospective destructions from drought in different areas of the environment, society and overall economy (Tigkas 2008; Tigkas et al. 2012). The indices are vital and practical elements for characterising drought and supporting policy makers for moderating its impacts on various water consumption sections, since they facilitate intricate interrelationships between several climatic variables. Noticeably, indices make it easier to transfer climate anomaly information to a wide range of audiences and assisting scientists in quantitative weather abnormality evaluations in terms of their intensity, frequency, areal extent and duration (Vangelis et al. 2013; Giannikopoulou et al. 2014). Moreover, when drought indices are utilised, the time steps are adapted and the thresholds of each index selected are considered for representing the levels of drought severity.
A high number of meteorological drought indices with different intricacy have been utilised in various climatic conditions of the world for many objectives. Examples for some of the most common drought indices are as follows: Crop moisture index (CMI), deciles, Palmer drought severity index (PDSI), Palmer hydrological drought index (PHDI), percent of normal, standardized anomaly index (SAI), rainfall anomaly index (RAI), standardized precipitation index (SPI) and soil moisture drought index (SMDI), and surface water supply index (SWSI) as well as indices linked to the normalised difference vegetation index (NDVI). For more details of the most common indices that are used during the last few decades, readers may refer to many studies such as Heim (2002). Moreover, McVicar and Jupp (1998) as well as AghaKouchak et al. (2015) reviewed the current and potential operational uses of remote sensing to aid decisions on drought assessment.
The World Meteorological Organization (WMO) has put forward the SPI as a universal drought index because of its capacity to be estimated for various reference periods adapting to the different response times of typical hydrological parameters to precipitation shortages (Vicente-Serrano et al. 2015). The index allows detection of different drought categories affecting different systems and areas. However, there are deficiencies associated with its failure to identify drought conditions determined not by a shortage of precipitation but by a higher than normal atmospheric evaporative demand. The failure of the SPI to capture a raised evaporative demand associated with climate change is challenging (Tsakiris and Vangelis 2005; Cook et al. 2014). Therefore, recent drought trend studies (Shahidian et al. 2012; Vicente-Serrano et al. 2014) and drought scenarios under potential climate change projections (e.g., Hoerling et al. 2012; Cook et al. 2014) depend on drought indices that take into account precipitation and the atmospheric evaporative demand. Applying such indices, Cook et al. (2014) showed that increased ETo not only intensifies drying in areas where precipitation is already decreased, it also drives regions into drought that would otherwise experience little drying or even wetting from precipitation trends alone.
Tigkas et al. (2012, 2015) introduced a summary of the RDI theory with some practical applications, the RDI is founded on the P, which is observed, and the ET, which is estimated. The RDI can be calculated for any time step, and can be effectively related with agricultural drought and directly linked to the climate conditions of the area. Generally, in case of higher temperatures, water demand is increasing; therefore, the RDI could be amended to be used as an indicator for future drought risk assessment related to the various sectors of water use. So, that the RDI is suitable for climate instability conditions studies.
Viviroli et al. (2007) assessed the typology, mapping, and global significance of mountains. The team also made recommendations regarding further research on climate change and mountain water resources (Viviroli et al. 2011). However, their research was more concerned with the potential changes in water resources as a result of climate change, as well as corresponding implications for water resources management, climate change adaptation and water policy.
Drought severity and aridity evaluation are impacted on by the potential impacts of ET methods, meteorological station elevation variations and climate conditions. A growing number of researchers in the field of water resources have recently used the RDI as a drought severity evaluation index (e.g., Tigkas et al. 2012; Vangelis et al. 2013; Giannikopoulou et al. 2014; Cai et al. 2015; Zarch et al. 2015), and they only used the standardised form without taking into consideration other forms and/or if there will be any change in the drought severity evaluation, if the ET methods changed and/or if the weather stations within the same basin have different elevations in addition to the impact of the regional climate conditions. For example, although Vangelis et al. (2013) assessed the potential impact of different ET methods on the drought severity computed by RDI, they only used data from semi-arid climates of the Mediterranean region and only for two meteorological stations without taking into consideration other semi-arid climatic conditions such as tropical and continental in addition to Sahara and humid conditions. Furthermore, they have just focused on the RDIst without giving any attention to the RDIα12. Therefore, to fill the acknowledge gap, this study has focused, in particular, on the alpha form, which is used for aridity evaluation attempting to answer the following questions:
-
1.
How can the ET method(s) impact on the RDI index outcomes, which in turn can change the drought severity and aridity evaluation?
-
2.
If the elevations of the meteorological stations that are located within the same basin would change, how would this alter the evaluation of the drought and aridity of the basin?
-
3.
For regional drought severity and aridity assessments, would changing climatic conditions impact on the ET estimations?
1.2 Rationale, Aim and Objectives
The current study target is to assess the potential impact of ET methods, elevation and climate conditions on the spatiotemporal variability of the RDI. The motivation to study the RDI index is the fact that it is depended on a combination of P and ET, which is considered more realistic than using P only. In addition, the RDI is a newly developed drought index and is used in several areas all over the word, particularly in semi-arid and arid regions, and became the acquisitioning base as a result of its low data requirements, high sensitivity, resilience and suitability for climate instability (Rossi and Cancelliere 2013; Vicente-Serrano et al. 2015; Zarch et al. 2015). The RDI provides physically thorough theoretical grounds for evaluation of the meteorological drought severity and aridity assessment. Therefore, it is important to evaluate the ET estimation impact, elevation and climate conditions on the aridity and drought severity characterization estimated by this index.
Accordingly, the main aim of the current research is to shed light on the three basic components of the RDI index, in particular, its RDIα12 form. The corresponding objectives are as follows:
-
to study the sensitivity of the RDI index;
-
To compare the selected methods Hargeaves (HG), Thornthwaite (ThW) and Blaney-Criddle (BC) with the FAO Penman-Monteith (PM) methodology for reference purposes;
-
To assess the impact of elevation variations for different climate conditions; and
-
To highlight the use of RDI as an aridity and climatic index.
To address these objectives, meteorological data from twenty-four stations all over the world describing semi-arid (Mediterranean (MD), Tropical (TR), and Continental (CN)), Sahara, and humid climatic conditions, representing both mountainous regions and lowlands, have been selected.
2 Theory
2.1 Evapotranspiration Estimation
The evapotranspiration (ET) estimation methods can be split into three main groups. The first one is known as hydrologic or water balance methods, which comprises physical techniques, and its application is restricted to the workshop environment.
The second group comprises analytical methods that are based on climatic parameters; in this group, evapo-transpiration processes are expressed by equations, which concentrate on the two key climatic component mass transport and energy balance. The PM and the Priestley-Taylor methodologies are recognized models of this group (Shahidian et al. 2012; Vangelis et al. 2013).
Empirical methods belong to the last group. The underlying assumption is that temperature is a good indicator of the evaporative influence of the atmospheric temperature. These methods became very common as a result of their low data requirements. The HG, ThW and BC equations are the most widely used methods representing this category, which has been considered in this study (see section 3). The following sub-sections provide short descriptions of all the aforesaid ET estimates.
2.1.1 Hargreaves Method
The Hargreaves method is an attractive methodology for the ET estimation as it is simple and reliable, requires only a few data is easy-to-compute and has a minimum impact associated with arid weather station results. This method is temperature-based, as it requires only the minimum and maximum values of temperature. The reader may refer to many researches such as Hargreaves and Samani (1982, 1985) for more details regarding this method. For a specific latitude and day, R A is usually estimated from published tables or calculated applying a group of equations (Xu and Singh 2001; Vangelis et al. 2013).
2.1.2 Thornthwaite Method
This method is one of the temperature-based empirical formula for calculation of ET, which is estimated on a monthly basis, and is given by Eq. (2).
where N is the average monthly possible sunshine hour (hr/day), m is the number of days of each month, T m is the mean monthly temperature (C°), and α is estimated by Eq. (3).
where I is a heat index for the year calculated according to Eq. (4).
Given the observed monthly average temperatures at a meteorological station, a prediction of the monthly evaporation of the year can be obtained. Despite the fact that this formula is shown by many researches to underestimate ET, it has been accepted widely around the globe (Vangelis et al. 2013).
2.1.3 Blaney–Criddle Method
The Blaney–Criddle method is popular and widely used, especially in semi-arid and arid climates, due to its simplicity and ease-of-use. The general form is shown in Eqs. (5) and (6).
where ET is the evapotranspiration (mm) from the reference crop, T m is the average temperature (°C), k is a monthly coefficient representing consumption, p is the ratio of the mean number of daylight hours in the day for the specified month over the total of daylight hours in the year, which is a function of the latitude of the study area and the month required. Despite the fact that the p value is normally estimated through tables, it can also be computed according to Eq. (7) (Vangelis et al. 2013).
where N i is the theoretical number of daytime hours i, and d 1 and d 2 are the last days of the month.
2.1.4 Food and Agriculture Organization Penman-Monteith Method
The FAO Penman-Monteith method is primarily applied to estimate the reference evapotranspiration (ET) as indicated in Eq. (8) according to McMahon et al. (2013).
where ET is the reference evapotranspiration (mm/day), R n is the net radiation at the crop surface (MJ/m2/day), G is the soil heat flux density (MJ/m2 × day), u 2 is the wind speed at 2-m elevation (m/s), e s is the saturation vapour pressure (kPa), e a. is the natural vapour pressure (kPa), e s -e a. is the saturation vapour pressure deficit (kPa), Δ is the slope vapour pressure curve (kPa/°C) and γ is the psychrometric constant (kPa/°C).
2.2 The Reconnaissance Drought Index (RDI)
This index can be formulated in alpha (RDIαk), normalised (RDIn) and standard (RDIst) forms. The RDIst can be used for drought severity assessments, whereas RDI αk can be applied as an aridity index. The index is mainly founded on the aggregated P and ET theories (Vangelis et al. 2013). The RDI is normally estimated using Eq. (9).
where P ij and ET ij represent precipitation and evapotranspiration of the j-th month of the i-th water year (the water year in, for example, Iraq begins in October), and N is the obtained weather data total year number.
The values of RDI αk match both the gamma and the lognormal distributions in various positions for various time scales for which they were examined (Tigkas 2008). Through applying the former distribution, RDIst can be computed by utilising Eq. (10).
where y i is the ln(α ki ), ӯ is its arithmetic mean and σ y is the corresponding standard deviation. Equation (11) can be used to calculate RDIst in the case of the gamma distribution application (Tigkas 2008).
where γ and β are the shape and scale parameters, respectively, and Γ(γ) is the gamma function. The spatiotemporal extent of the gamma probability distribution parameters γ and β can be predicted for 3, 6, 9 and 12 months. The γ and β are estimated by the maximum likelihood method as shown in Eqs. (12) to (14).
When the cumulative precipitation datasets for the selected reference period contain zeros, the gamma function cannot be defined for x = 0. Therefore, a composite cumulative probability function (Eq. (15)) might be utilised.
where q is the likelihood of zero precipitation and G(x) is the gamma distribution cumulative probability. The probability of zero precipitation (q) can be computed by m/N if m is the zeros number in the α k time series. The gamma distribution cumulative probability G(x) is replaced by the cumulative probability H(x).
Compared to the natural conditions, a positive value of RDIst relates to a wet period. The drought severity increases when RDIst numbers are minimal and it can be classified into mild, moderate, severe and extreme classes. The respective limits of RDIst are −0.5 to −1.0, −1.0 to −1.5, −1.5 to −2.0, and <−2.0, respectively. The RDI can be estimated for different time steps such as 3-, 6-, 9- and 12-month (Tigkas et al. 2012). This indicates a variable quality of RDI compared to other drought indices since it is computed for pre-determined reference periods. Additionally, arid regions are defined into dry sub-humid, semi-arid, arid and hyper-arid classes, and the corresponding limits of RDIα12 are 0.50 to 0.75, 0.20 to −0.50, 0.03 to 0.20, and <0.03, respectively (UNESCO 1979).
3 Materials, Data and Methods
3.1 Climate Forecasting System Reanalysis Data
The climate forecasting system reanalysis data are based on a dataset created by the National Centres for Environmental Prediction (NCEP) as a part of the climate forecast system (Dile and Srinivasan 2014; Saha et al. 2014). These data are applied in this study to gain historical data and to investigate its applicability for drought severity assessments.
The CFSR dataset supersedes the previous NCEP/NCAR reanalysis dataset that has been immensely utilised in previous down-scaling research (e.g., Wilby et al. 1998; Michelangeli et al. 2009; Higgins et al. 2010; Maurer et al. 2010). The CFSR dataset covers the period from 1979 to the present, and has a resolution of nearly 0.25 degrees around the equator and to 0.5 degrees in non-tropical regions (Higgins et al. 2010). Concerning data reliability in watershed-scale modeling, Fuka et al. (2014) confirmed that applying the CFSR data as input to the hydrological model produces discharge simulations that are as accurate as or even better than models derived thought popular stations, particularly in the case that the stations are located greater than 10 km from the area of interest. Additionally, gathering representative weather data for basin-scale hydrological simulations might be challenging and time-consuming. This is because the land-based meteorologiacl stations do not usually adequately cover the climate occurring over a basin for many reasons such as that they might be located far from the area of interest and are associated with missing data.
For the purpose of this article, the CFSR dataset has been applied for two different elevations representing typical lowland and mountainous stations that were selected from semi-arid (MD, TR, and CN), Sahara and humid climatic regions (Fig. 1). Table 1 shows the categories and locations of the chosen stations. For example, the gridded station labelled “HL” is situated at an elevation (1677 m) representing a mountainous area in the East of Al-Sudan (22° 0′ 36″N, 36° 15′ 0″E), while the station that is labelled “LL” is situated at a low elevation (40 m) in the UK (52° 55′ 12″ N, 3° 45′ 0″ W). The average yearly precipitation and temperature for the first location is 1118 mm and 24.7 °C, respectively. The corresponding means for the second station are 155 mm and 9.1 °C, respectively. Reliable monthly data of minimum and maximum temperature, precipitation, relative humidity and wind speed were sourced.
Initially, the data were examined for their validity, minor emendations and filling of some gaps were implemented depending on customary statistical practices. After that, ET was estimated by the three considered methods (Fig. 2).
The next step involved the calculation of annual values of RDIα12, RDIst, and RDIn, depending on ET values estimated by various methods with the aid of the software tool called drought indices calculator (DrinC) as reported by Tigkas et al. (2015).
3.2 Data Analysis
ArcGIS 10.3 has been used for gridded meteorological station projections on the world borders Shapefile that has been downloaded from Thematic Mapping (2009). Statistical analyses for the daily data, including monthly and annually average values, corrections and gap filling were performed using the Statistical Program for Social Sciences (SPSS) 20. One-way ANOVA analysis has been achieved using Daniel’s XL Toolbox, which is a free, open-source add-in for Excel. Whereas, estimating ET and RDI were accomplished with a specialized software package named DrinC (Tigkas et al. 2012, 2015).
3.3 Evaluation of the Performance
The root mean square error (RMSE) and the mean bias error (MBE) are two of the most widely accepted statistical indicators, which have been selected to compare the effect of various ET estimates on various RDI form values. Equation (16) is used to compute RMSE.
The MBE is estimated by Eq. (17).
where n represents the total number of observations (in both equations), X ob and X es are the estimated values by the equation used as a standard in each case and the computed value by each equation under review, this is because there are no measured data available. The ideal value of both RMSE and MBE is zero (Vangelis et al. 2013).
4 Results and Discussion
The selection of the best ET estimate for a specific climate and elevation is important. This is required since the application of different approaches may result in flaws in estimations of water resources availability. Therefore, one of the study objectives is to analyse the ET estimate impacts on aridity and drought evaluations. It is critical to note that for all climatic conditions, ThW produced lower values, except for humid climate as HG is linked to lower ET values, whereas the PM had the highest ones. Differences of about 1000, 500, 750, 1000 and 1250 mm in terms of mean values were calculated for MD, TR, CN, Sahara and humid climates, respectively. The HG and PM formulas follow the same annual pattern with rather alike variations around their average numbers in the same periods. However, a diverse variation pattern is followed by ThW. This result confirms findings by Vangelis et al. (2013).
The difference among all locations is that the amounts estimated by ThW are mostly lower than the values calculated by the other two methods for MD, TR, CN and Sahara climates. Moreover, it can be observed that ThW strongly underestimates ET under dry and arid conditions and at elevated elevations since the equation does not take into account the air saturation deficit, it is mainly calibrated for temperate climates at low elevations.
Whereas BC estimates rather accurately with no large under- or over-estimates the majority of the time series, the obtained results using BC are close to the numbers produced by HG, particularly for the MD, TR and CN regions. Moreover, for the humid regions, the BC methodology was linked to the best findings (similar to the full equation of PM). Accordingly, the HG could be considered as the main method to estimate ET for almost all selected regions due to its suitability for climate change studies. The superiority of the HG is supported by several research studies in the field (Vangelis et al. 2013; Tigkas et al. 2015).
Then, and to evaluate the potential impacts of ET methods on the drought severity assessment, Tables 1 and 2 show the RDIn and RDIst values, which could be considered approximately the same regardless of elevation and ET estimation used for most of MD, TR and Sahara climates. Slight variations, which appear for few years are not significant, because they do not impact on drought severity as indicated by the RDI index. The different numbers, despite their variations, are in the same drought severity category without surpassing a drought severity threshold. No significant differences (P > 0.05) (part of the analysis are not presented) were noted for RDIn and RDIst values produced by the numerous ET methodologies for most of the MD, TR and Sahara areas. However, this could not the case for smaller periods such as 3, 6, and 9 months, therefore, it is suggested to use such periods for further research.
Furthermore, RDIst and RDIn values for many other geographical regions such as South Russia, UK and East Brazil are significantly (P < 0.05) different for various elevations using the three ET methods compared to PM (Tables 1 and 2). The differences are considered important since they affect drought severity reported by the RDIst, and different values give completely different drought severity categories for almost all periods. This would become even clearer for shorter periods such as 3, 6 and 9 months, which is why it is highly recommended to use such periods for future research.
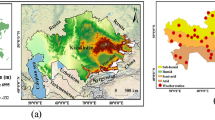
Regional aridity evaluations can alter due to many factors such as the specific ET method used and weather station elevations. Table 3 reveals the following: No significant aridity variations were found with respect to different ET estimates for different elevations in the West Australia, East Brazil, Sahara and Al-Sudan geographical regions. Figure 3a, b show the results for only West Australia as an example. Marginal differences, which are revealed for many years, cannot be seen as important since they do not influence aridity evaluation. The different numbers, despite their fluctuations, stay constant for the two main elevations in the same aridity class without exceeding any threshold value. However, this could not be the case for smaller periods of time. This is why RDIα12 values for shorter reference periods than the annual one are recommended.
For the MD and CN climatic conditions in South Africa, South USA and South East Spain, Fig. 3c, d as well as Table 3 present results for South Africa as an example confirming that there is considerable variation in RDIα12 values for different elevations using different ET estimates, which in turn affect significantly regional aridity assessments. Despite the fact that values of RDIα12 produced by the HG and BC methods are not similar to the results of the reference method, they are rather identical and the most significant (P < 0.05) deviations are shown by the ThW method.
Moreover, no significant (P > 0.05) differences were detected in the RDIα12 values estimated by the ET methods (particularly, the HG method) at low elevations in North Iraq (Fig. 3e, f), East China and South Russia. Whereas at mountainous locations, significant (P < 0.05) RDIα12 values were noted using different ET estimates (Table 3).
Regarding RDIα12 for humid climatic conditions such as the UK, Fig. 3g, h as well as Table 3 show that at both elevations the selected methods are underestimating ET (particularly, the BC method) so that using such methods can lead to completely different aridity categories for mountainous locations.
Another objective of this study was to present RDIα12 as a climatic index. Figure 4a shows the RDIα12 values for different climatic conditions. Note that RDIα12 is significantly (P < 0.05) higher for humid areas regarding the whole time series and linked to higher fluctuations compared to other climatic conditions. Furthermore, RDIα12 is higher for the mountainous locations for the complete time series and related to higher variability compared with lowland locations (Fig. 4b). Eventually, and for explanation purposes, Fig. 4c, d represent how RDIst and RDIn values at a specific region and climate condition can be changed with considerable fluctuations corresponding to different elevations.
a The annual reconnaissance drought index alpha form (RDIα12) form values for different climatic conditions; b different elevations; c The normalised annual reconnaissance drought index (RDIn) values for different elevations; and d The standardised annual reconnaissance drought (RDIst) index values for different elevations
Apart from the above, the authors suggest using any of the examined ET methods for RDIst and RDIn estimations with the aim to circumvent the ThW equation, particularly for mountainous locations. Furthermore, the HG method provides the most accurate results. Since RDI utilises the critical part of evapotranspiration but retaining the need for data to a minimum, the HG and BC methods are the most appropriate choices for computing ET for the RDI in many regions (particularly in semi-arid and arid ones). However, in the case of the long-term reliable datasets availability of several weather parameters, researchers should use PM estimates.
5 Conclusions and Recommendations
The following conclusions could be drawn: No significant (P > 0.05) influence on RDIst and RDIn was detected through the selected ET estimates at different elevations for the MD, TR and Sahara climates. Slight differences revealed for many years cannot be seen as important, because they do not impact drought severity indicated by RDI. The different numbers, despite their variations, stay in the identical category of drought severity without surpassing a drought severity threshold. However, this could not be the case for smaller periods of time, so that it is highly recommended to use shorter time steps such as 3, 6 and 9 months for further research.
In addition, for many regions such as South Russia, the UK, and East Brazil, RDIst and RDIn values are significantly (P < 0.05) different for various elevations using the three selected ET methods compared against PM. The differences are considered significant (P < 0.05), since they affect dramatically the drought severity reported by RDIst. The difference would become clearer for shorter time periods. Therefore, it is highly recommended to use time steps such as 3, 6 and 9 months for further research.
Furthermore, RDIα12 is directly influenced by the selected ET method at different elevations for all regions. This is why the method of ET, particularly at high elevation, is important. Accordingly, the application of different approaches may lead to errors in water resources availability and water quality predictions. A significant (P < 0.05) deviation has been observed when the RDIα12 is computed using different ET methods. Differences were noted from region to region and for various elevations. Furthermore, for nearly all cases studied and for the selected elevations, it has been observed that the HG method performed relatively better than the others. This research should be undertaken again for other regions and climatic conditions to evaluate the impact of elevation on the choice of ET method and the calculation of the RDIα12. Assessments for shorter reference time periods than the annual time step are also recommended. This should lead to a further generalisation of the research conclusions.
References
Aghakouchak A, Farahmand A, Melton FS et al (2015) Remote sensing of drought: progress, challenges and opportunities. Rev Geophys 53(2):452–480
Cai W, Zhang Y, Chen Q, Yao Y (2015) Spatial patterns and temporal variability of drought in Beijing-Tianjin-Hebei metropolitan areas in China. Adv Meteorol 2015(289471):1–14
Cook BI, Smerdon JE, Seager R, Coats S (2014) Global warming and twenty-first century drying. Clim Dyn 43(9):2607–2627
Dile YT, Srinivasan R (2014) Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: an application in the Blue Nile River basin. J Am Water Resour Assoc (JAWAR) 50(5):1226–1241
Fuka DR, Walter MT, MacAlister C et al (2014) Using the climate forecasting system reanalysis as weather input data for watershed models. Hydrol Process 28(22):5613–5623
Giannikopoulou AS, Kampragkou E, Gad FK et al (2014) Drought characterisation in Cyclades complex, Greece. Eur Water 47:31–43
Hargreaves GH, Samani ZA (1982) Estimation of potential evapotranspiration. J Irrig Drain Div, Proceeding of the American Society of Civil Engineering 108:223–230
Hargreaves GH, Samni ZA (1985) Reference crop evapotranspiration from temperature. Trans Am Soc Agric Eng 51(4):1295–1310
Heim RR (2002) A review of twenty-century drought indices used in the united state. Bull Am Meteorol Soc 83(8):1149–1165
Higgins RW, Kousky VE, Silva VBS et al (2010) Intercomparison of daily precipitation statistics over the United States in observations and in NCEP reanalysis products. J Clim 23(17):4637–4650
Hoerling MP, Eischeid JK et al (2012) Is a transition to semi-permanent drought conditions imminent in the U.S. Great Plains? J Clim 25:8380–8386
Maurer EP, Hidalgo HG, Das T et al (2010) The utility of daily large-scale climate data in the assessment of climate change impacts on daily streamflow in California. Hydrol Earth Syst Sci 14(6):1125–1138
McMahon TA, Peel MC, Lowe L et al (2013) Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: a pragmatic synthesis. Hydrol Earth Syst Sci 17:1331–1363
McVicar TR, Jupp DLB (1998) The current and potential operational uses of remote sensing to aid decisions on drought exceptional circumstances in Australia: a review. Agric Syst 57(3):399–468
Michelangeli PA, Vrac M, Loukos H (2009) Probabilistic downscaling approaches: application to wind cumulative distribution functions. Geophys Res Lett 36(11):1–6
Rossi G, Cancelliere A (2013) Managing drought risk in water supply systems in Europe: a review. Int J Water Resour Dev 29(2):272–289
Saha S, Moorthi S, Wu X et al (2014) The NCEP climate forecast system version 2. J Clim 27(6):2185–2208
Shahidian Sh, Serralheiro R, Serrano J et al. (2012) Hargreaves and other reduced-set methods for calculating evapotranspiration. In: Irmak A (ed) Evapotranspiration: remote sensing and modelling. InTech, pp 50–80. ISBN 978–953–307-808-3
Thematic mapping (2009) [Online] Available from: http://thematicmapping.org/downloads/world_borders.php. [Accessed: 2nd October 2015]
Tigkas D (2008) Drought characterisation and monitoring in regions of Greece. Eur Water 23(24):29–39
Tigkas D, Vangelis H, Tsakiris G (2012) Drought and climatic change impact on streamflow in small watersheds. Sci Total Environ 440:33–41
Tigkas D, Vangelis H, Tsakiris G (2015) DrinC: a software for drought analysis based on drought indices. Earth Sci Inform 8(3):697–709
Tsakiris G, Vangelis H (2005) Establishing a drought index incorporation evapotranspiration. Eur Water 9(10):3–11
United Nations Educational, Scientific and Cultural Organization (UNESCO) (1979) Map of the world distribution of arid regions: Map at scale 1:25,000,000 with explanatory note. MAB Technical Notes 7, UNESCO, Paris
Vangelis H, Tigkas D, Tsakiris G (2013) The effect of PET method on reconnaissance drought index (RDI) calculation. J Arid Environ 88:130–140
Vicente-Serrano SM, Lopez-Moreno J, Begueria S et al (2014) Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ Res Lett 9:044001
Vicente-Serrano SM, Schrier GVD, Begueria S et al (2015) Contribution of precipitation and reference evapotranspiration to drought indices under different climates. J Hydrol 526:42–54
Viviroli D, Durr HH, Messerli B et al (2007) Mountains of the world, water towers for humanity: typology, mapping, and global significance. Water Resour Res 43(7):1–13
Viviroli D, Archer DR, Buytaert W et al (2011) Climate change and mountain water resources: overview and recommendations for research, management and policy. Hydrol Earth Syst Sci 15(2):471–504
Wilby LR, Hassan H, Hanaki K (1998) Statistical downscaling of hydrometeorological variables using general circulation model output. J Hydrol 205(1–2):1–19
Xu CY, Singh VP (2001) Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrol Process 15(2):305–319
Zarch MAA, Sivakumar B, Sharma A (2015) Droughts in a warming climate: Aglobal assessment of standardized precipitation index (SPI) and reconnaissance drought index (RDI). J Hydrol 526:183–195
Acknowledgements
The research presented has been financially supported by the Iraqi Government. Thanks go to Dr. Furat Al-Faraj assisted in the early stage of this research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mohammed, R., Scholz, M. Impact of Evapotranspiration Formulations at Various Elevations on the Reconnaissance Drought Index. Water Resour Manage 31, 531–548 (2017). https://doi.org/10.1007/s11269-016-1546-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-016-1546-9